Building Phylogenies Parsimony 1 Methods Distance-based

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕГИСТРАЦИЯ

Building Phylogenies Parsimony 1

Methods • Distance-based • Parsimony • Maximum likelihood

Note • Some of the following figures come from: – [S 05] Swofford http: //www. csit. fsu. edu/~swofford/bioin formatics_spring 05 – [F 05] Felsenstein http: //evolution. gs. washington. edu/gs 54 1/2005/

Parsimony methods • Goal: Find the tree that allows evolution of the sequences with the fewest changes. • This is called a most parsimonious (MP) tree • Parsimony is implemented in PAUP* http: //paup. csit. fsu. edu/ • Compatibility methods are closely related to parsimony: – Goal: Find tree that perfectly fits the most characters.

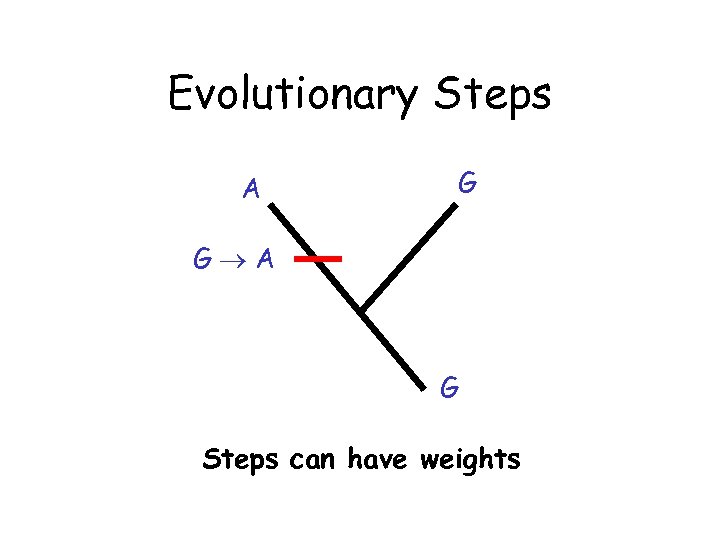
Evolutionary Steps A G G A G Steps can have weights

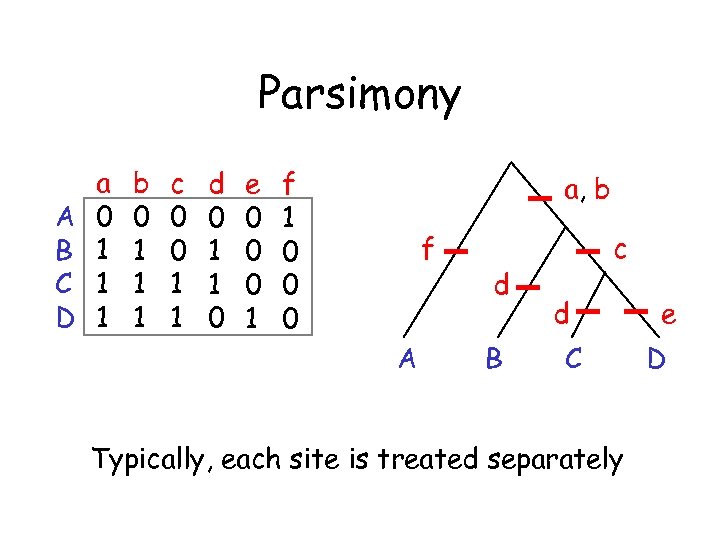
Parsimony A B C D a 0 1 1 1 b 0 1 1 1 c 0 0 1 1 d 0 1 1 0 e 0 0 0 1 f 1 0 0 0 a, b f A d B c d C Typically, each site is treated separately e D

Some numbers Number of unrooted trees on n 2 species: Un = (2 n 5)(2 n 7)(2 n 9). . . (3)(1), Number of rooted trees on n 3 species: Rn = (2 n 5) Un

The number of rooted trees [F 05]

Small versus Large Parsimony • Parsimony score of a tree: The smallest (weighted) number of steps required by the tree • (Large) Parsimony: Find the tree with the lowest parsimony score • Small Parsimony: Given a tree, find its parsimony score • Small parsimony is by far the easier problem. – Used to solve large parsimony

A DNA data set [F 05]

An example tree [F 05]

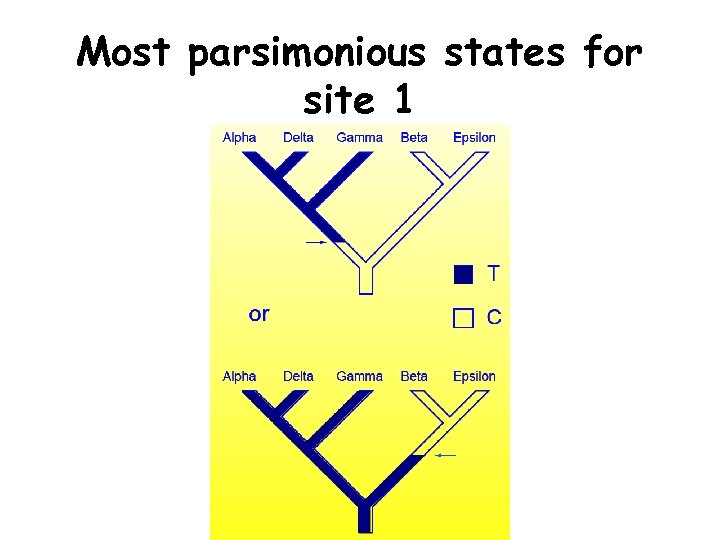
Most parsimonious states for site 1

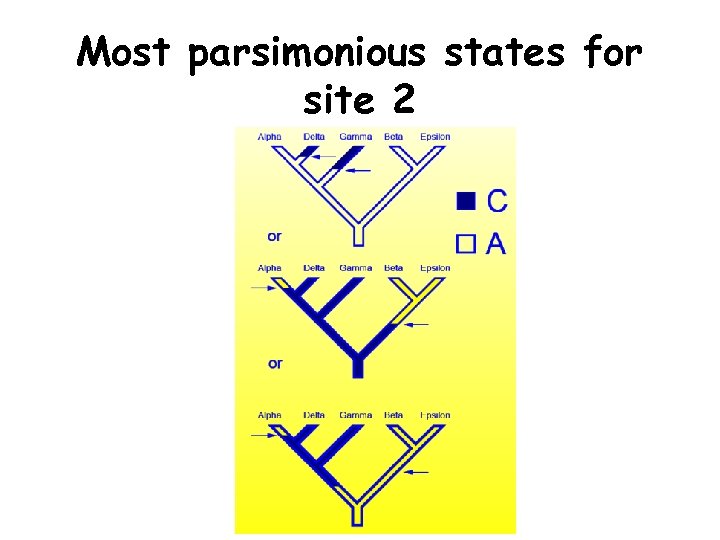
Most parsimonious states for site 2

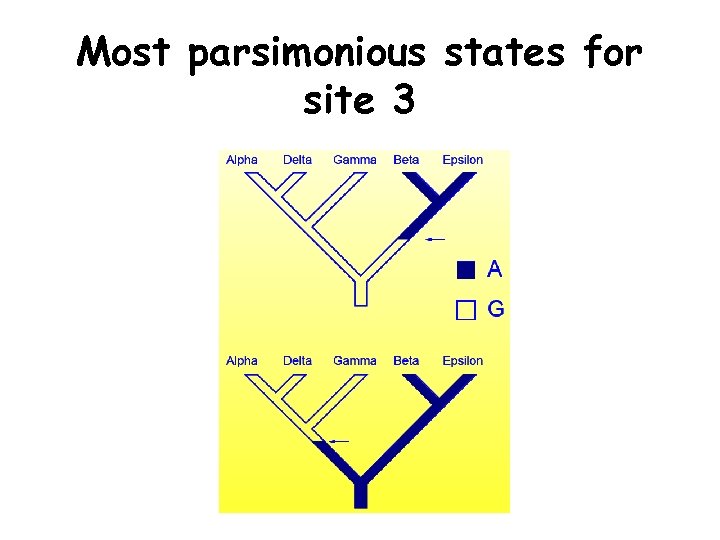
Most parsimonious states for site 3

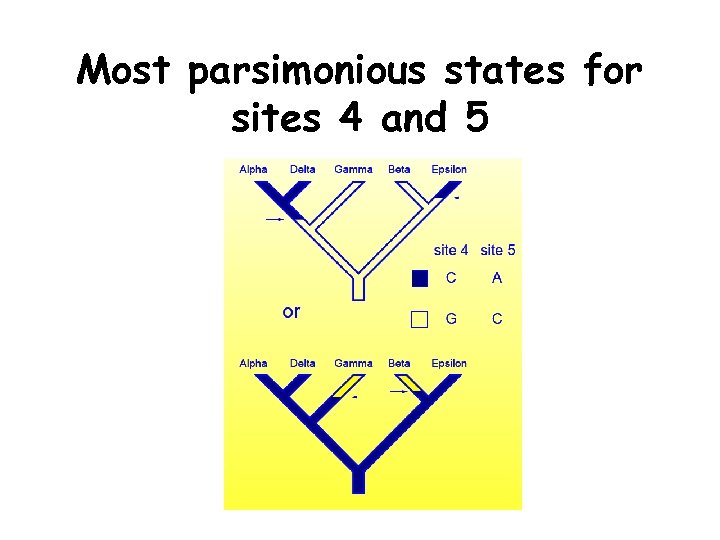
Most parsimonious states for sites 4 and 5

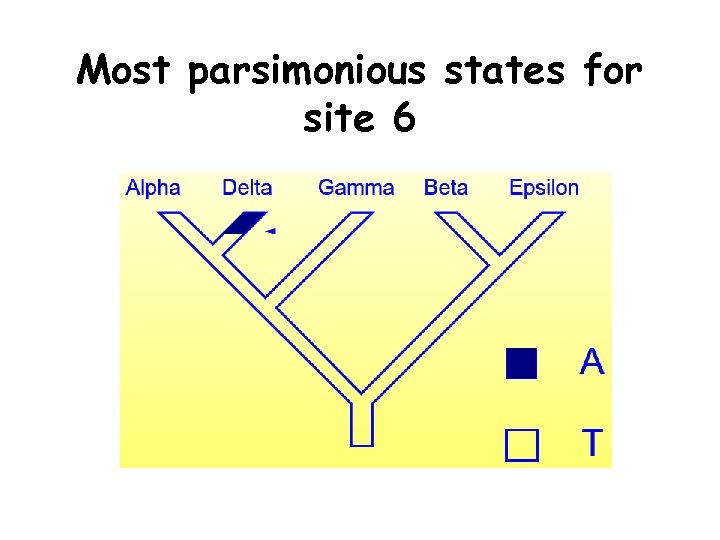
Most parsimonious states for site 6

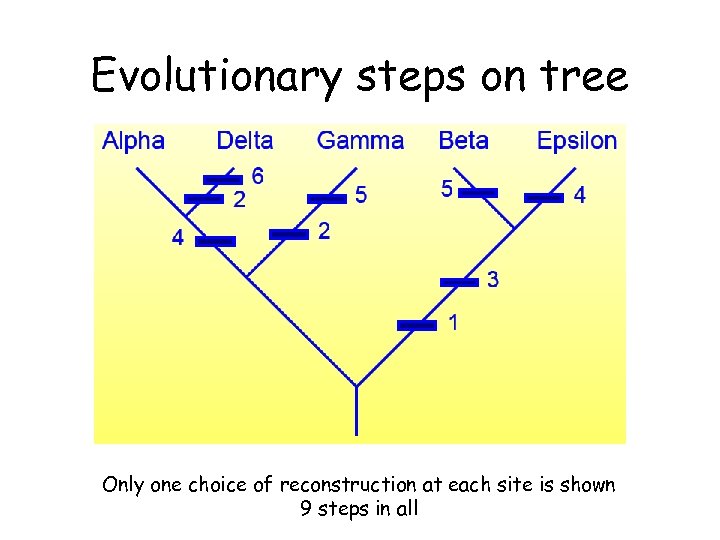
Evolutionary steps on tree Only one choice of reconstruction at each site is shown 9 steps in all

Algorithms for Small Parsimony • Fitch’s algorithm: – Based on set operations – Evolutionary steps have same weight • Sankoff’s algorithm: – Based on dynamic programming – Allows steps to have different weights • Both algorithms compute the minimum (weighted) number of steps a tree requires at a given site.

Fitch’s Algorithm • Each node v in tree has a set X(v) • If v is a leaf (tip), X(v) is the nucleotide observed at v – if there is ambiguity, X(v) contains all possible nucleotides at v • If v is a node with descendants u and w, – Let Y X(u) X(w) – If Y make X(v) Y, – If Y make X(v) X(u) X(w) and count one step.

Fitch’s Algorithm: Example [F 05]

Sankoff’s Algorithm • Let cij be the cost of going from state i to state j. • E. g. , transitions (A G or C T) are more probable than transversions, so give lower weight to transitions • Let Sv(k) be the smallest (weighted) number of steps needed to evolve the subtree at or above node v, given that node v is in state k.

Sankoff’s Algorithm • If v is a leaf (tip) • If v is a node with descendants u and w • The minimum number of (weighted) steps is

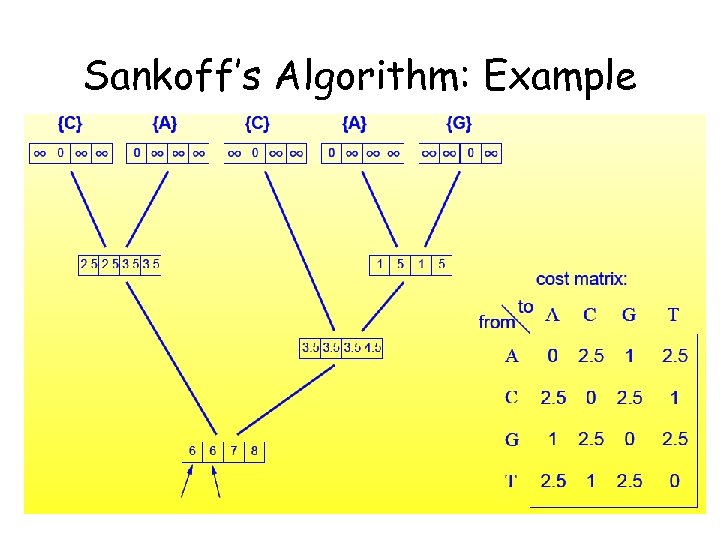
Sankoff’s Algorithm: Example

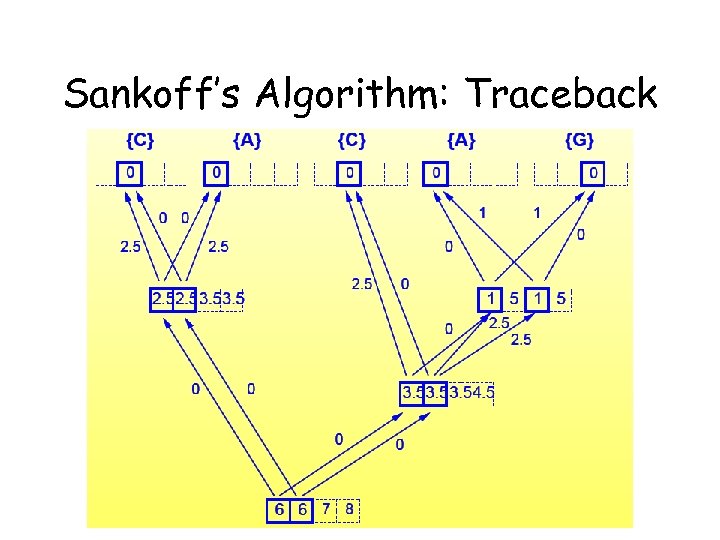
Sankoff’s Algorithm: Traceback

Searching for an MP tree • Exhaustive search (exact) • Branch-and-bound search (exact) • Heuristic search methods – Stepwise addition – Branch swapping – Star decomposition

Homology, orthology, and paralogy • Homology: Similarity attributed to descent from a common ancestor. • Orthologous sequences: Homologous sequences in different species that arose from a common ancestral gene during speciation; may or may not be responsible for a similar function. • Paralogous sequences: Homologous sequences within a single species that arose by gene duplication.

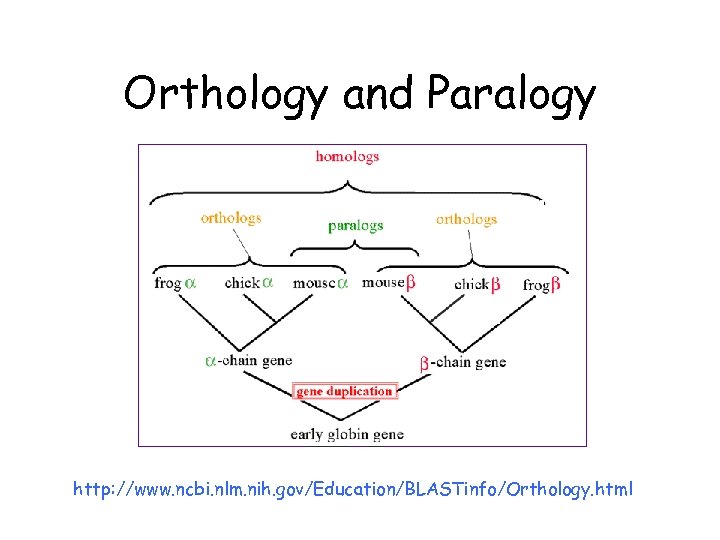
Orthology and Paralogy http: //www. ncbi. nlm. nih. gov/Education/BLASTinfo/Orthology. html

Скачать презентацию Building Phylogenies Parsimony 1 Methods Distance-based

5d25819a387f2aa36e573d2ef7961004.ppt

Количество слайдов: 27