Bridging scales Ab initio molecular dynamics and kinetic

Bridging scales: Ab initio molecular dynamics and kinetic Monte Carlo simulations Karsten Reuter Fritz-Haber-Institut, Berlin

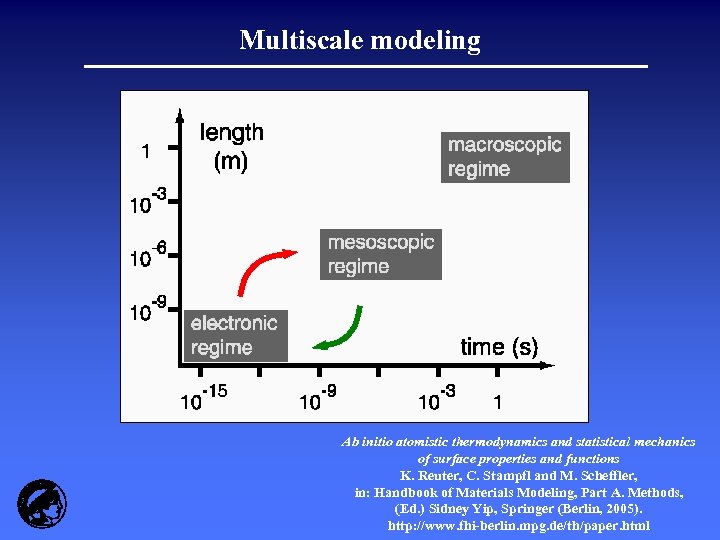
Multiscale modeling Ab initio atomistic thermodynamics and statistical mechanics of surface properties and functions K. Reuter, C. Stampfl and M. Scheffler, in: Handbook of Materials Modeling, Part A. Methods, (Ed. ) Sidney Yip, Springer (Berlin, 2005). http: //www. fhi-berlin. mpg. de/th/paper. html

I. Straightforward time-evolution: Ab initio molecular dynamics Understanding Molecular Simulation, D. Frenkel and B. Smit, Academic Press (2002)

MD: Numerical integration of Newton’s equation e. g. Verlet algorithm Solid-state: Δt ~ 10 -15 s Alternative algorithms: - velocity Verlet - leapfrog - predictor-corrector - Runge-Kutta …

Keeping everything: expensive, limited time scale Example: O 2 dissociation at Al(111) Total time of trajectory: 0. 5 ps Time step: 2. 5 fs (200 steps) CPU cost: 45 days on 1 Compaq ES 45 processor J. Behler et al. , Phys. Rev. Lett. 94, 036104 (2005)

II. First-principles kinetic Monte Carlo simulations: rare events and long time scales IPAM tutorial by Kristen Fichthorn http: //www. ipam. ucla. edu/publications/matut_5907. ppt

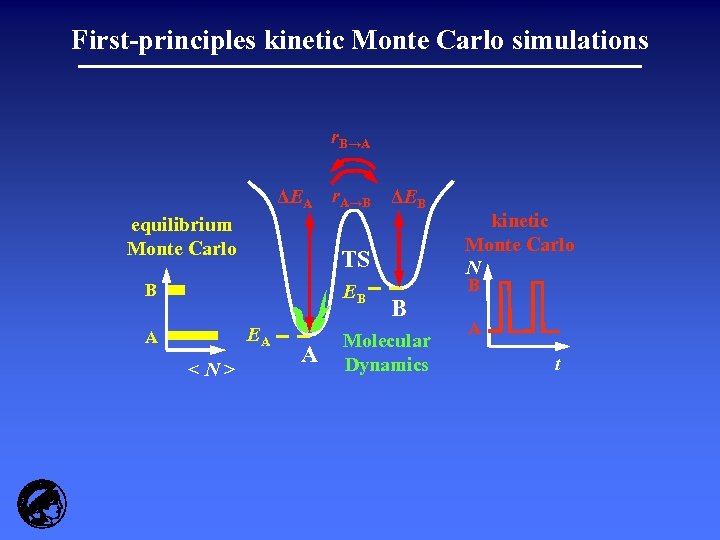
First-principles kinetic Monte Carlo simulations r. B→A ΔEA r. A→B ΔEB equilibrium Monte Carlo TS B EB EA A <N> A B Molecular Dynamics kinetic Monte Carlo N B A t

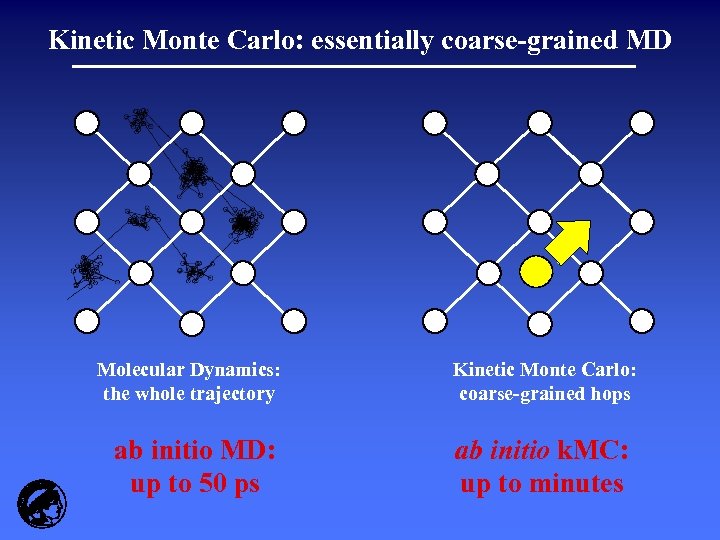
Kinetic Monte Carlo: essentially coarse-grained MD Molecular Dynamics: the whole trajectory ab initio MD: up to 50 ps Kinetic Monte Carlo: coarse-grained hops ab initio k. MC: up to minutes

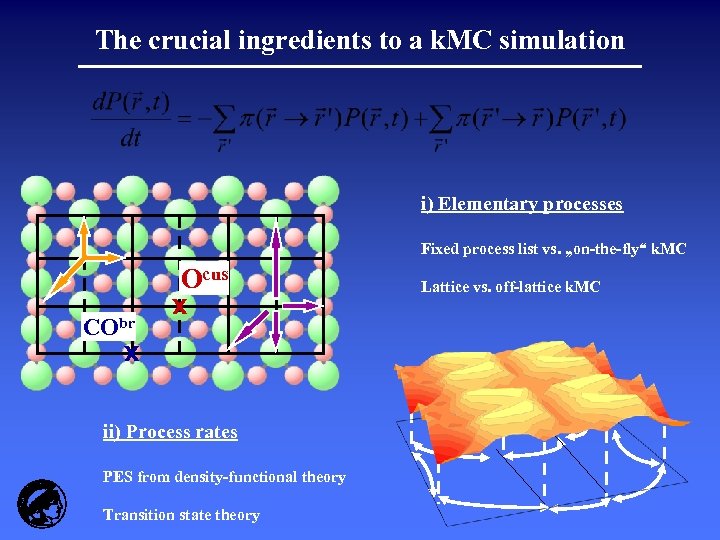
The crucial ingredients to a k. MC simulation i) Elementary processes Fixed process list vs. „on-the-fly“ k. MC CObr Ocus x x ii) Process rates PES from density-functional theory Transition state theory Lattice vs. off-lattice k. MC

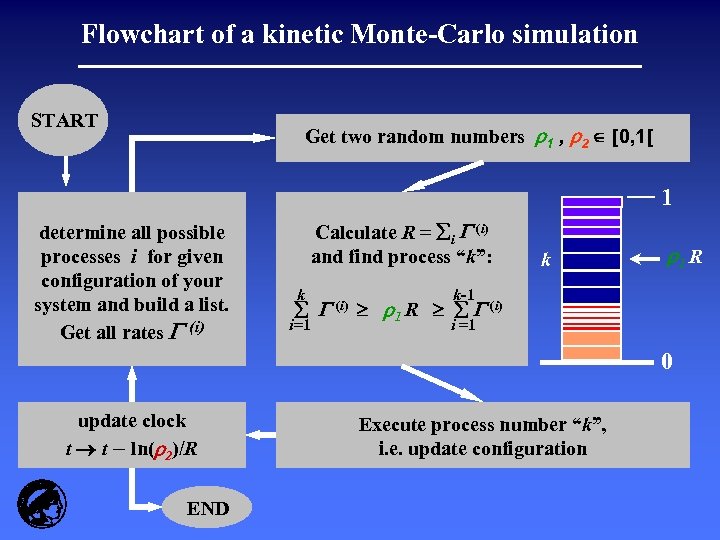
Flowchart of a kinetic Monte-Carlo simulation START Get two random numbers r 1 , r 2 [0, 1[ 1 determine all possible processes i for given configuration of your system and build a list. Get all rates (i) Calculate R = i (i) and find process “k”: k i=1 (i) k r 1 R k-1 r 1 R (i) i =1 0 update clock t t – ln(r 2)/R END Execute process number “k”, i. e. update configuration

III. Getting the rates… Chemical kinetics, J. K. Laidler, Harper & Row 3 rd ed. (New York, 1987) Methods for finding saddle points and minimum energy paths, G. Henkelman, G. Jóhannesson, and H. Jónsson, in “Progress on theoretical chemistry & physics”, S. D. Schwartz (Ed. ), Kluwer (Amsterdam, 2000)

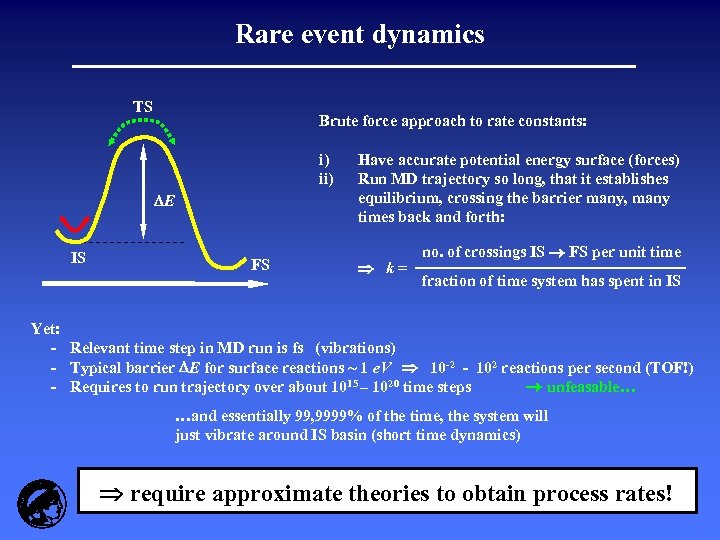
Rare event dynamics TS Brute force approach to rate constants: i) ii) E IS FS Have accurate potential energy surface (forces) Run MD trajectory so long, that it establishes equilibrium, crossing the barrier many, many times back and forth: k= no. of crossings IS FS per unit time fraction of time system has spent in IS Yet: - Relevant time step in MD run is fs (vibrations) - Typical barrier E for surface reactions ~ 1 e. V 10 -2 - 102 reactions per second (TOF!) - Requires to run trajectory over about 1015 – 1020 time steps unfeasable… …and essentially 99, 9999% of the time, the system will just vibrate around IS basin (short time dynamics) require approximate theories to obtain process rates!

Transition state (activated complex) theory I ( Eyring, Evans, Polanyi, ~1935 ) Assumptions: i) Reaction system passes the barrier only once (no recrossings) X ii) Energy distribution of reactant DOF is Boltzmannlike (many collisions compared to reaction events yield equilibrium between activated complex and IS, except with respect to the reaction coordinate) X iii) iv) eq. Passage over barrier is the motion of only one DOF, the reaction coordinate, which is independent of all other motions of the activated complex (no concerted motions) IS FS Passage over barrier is a classical event (no tunneling) Derivation: see e. g. K. J. Laidler, Chemical kinetics, Harper & Row, New York (1987) k. TST IS FS = [( k. T h )e S/k ] e- E/k. T

Transition state (activated complex) theory II - If assumptions i)-iv) are fulfilled, k. TST is exact. In general, k. TST is an upper limit to the real rate k = fdyn k. TST In principle, one can compute so-called dynamical corrections. In contrast to liquid & gas phase, fdyn ~ 1 for solid-state processes ( TST is a rather good approximation) - Attempt frequency/preexponential factor ko. TST = k. T S/k e h ~ 1013 sec-1 ~1 - In harmonic TST, ko. TST is given by the harmonic normal modes at the IS and TS (as explained in talk by Christian Ratsch on Tuesday) Þ problem reduces to locating transition states, i. e. saddle points in high dimensional PES

Transition state search algorithms I: grid and drag i) Grid method: - Compute PES on a (regular) grid - Scales like: (no. of points) dim - e. g. 59 ~ 2 million grid points x x often unfeasable x x ii) Drag method: x - Choose appropriate reaction coordinate q - Constrain q and relax all other DOF - Move from IS to FS highly dependent on good reaction coordinate hysteresis! FS x x IS x xx x TS

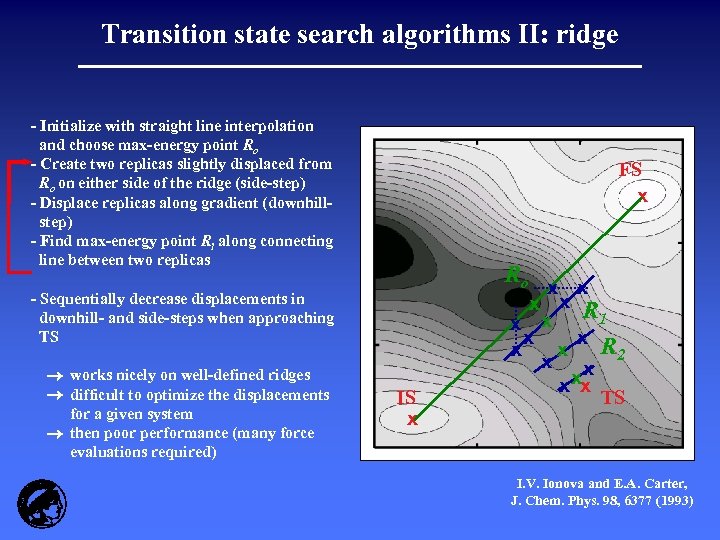
Transition state search algorithms II: ridge - Initialize with straight line interpolation and choose max-energy point Ro - Create two replicas slightly displaced from Ro on either side of the ridge (side-step) - Displace replicas along gradient (downhillstep) - Find max-energy point Ri along connecting line between two replicas FS x Ro - Sequentially decrease displacements in downhill- and side-steps when approaching TS works nicely on well-defined ridges difficult to optimize the displacements for a given system then poor performance (many force evaluations required) IS x x x R 1 x x R x x 2 x x xx x TS I. V. Ionova and E. A. Carter, J. Chem. Phys. 98, 6377 (1993)

Transition state search algorithms III: nudged elastic band - Initialize with several images {Ri} along a straight-line interpolation - Minimize S(R 1, …, RN) = E(R ) + k/2 (R i i+1 FS x - R i )2 - Problem: - elastic band cuts corners - images tend to slide down towards low-energy IS/FS regions, leaving few images for relevant TS region - Solution: - only spring force component parallel to path (no corner cutting) - only true force component perpendicular to path (no down-sliding) x x x IS x widely applied workhorse has problems, if energy varies largely along path, but very little perpendicular to it (kinky PES) x F || spring x Ftrue xx TS G. Mills and H. Jónsson, Phys. Rev. Lett. 72, 1124 (1994)

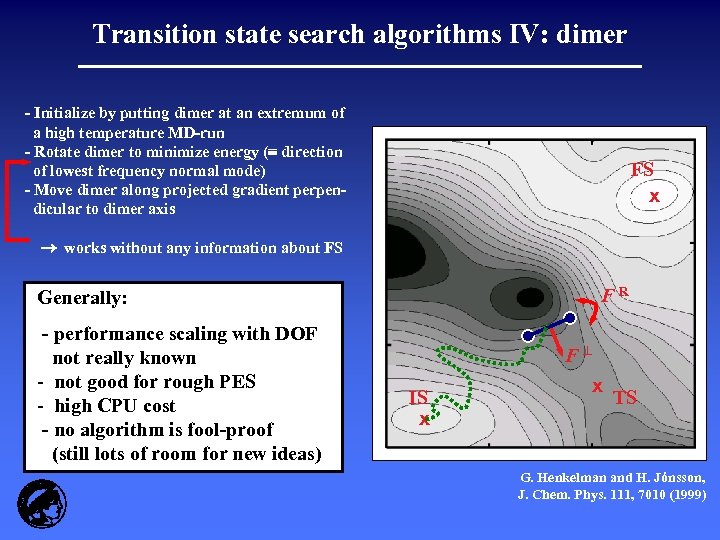
Transition state search algorithms IV: dimer - Initialize by putting dimer at an extremum of a high temperature MD-run - Rotate dimer to minimize energy ( direction of lowest frequency normal mode) - Move dimer along projected gradient perpendicular to dimer axis FS x works without any information about FS FR Generally: - performance scaling with DOF not really known - not good for rough PES - high CPU cost - no algorithm is fool-proof (still lots of room for new ideas) F IS x x TS G. Henkelman and H. Jónsson, J. Chem. Phys. 111, 7010 (1999)

IV. Identifying the processes… Extending the time scale in atomistic simulation of materials, A. F. Voter, F. Montalenti and T. C. Germann, Annu. Rev. Mater. Res. 32, 321 (2002)

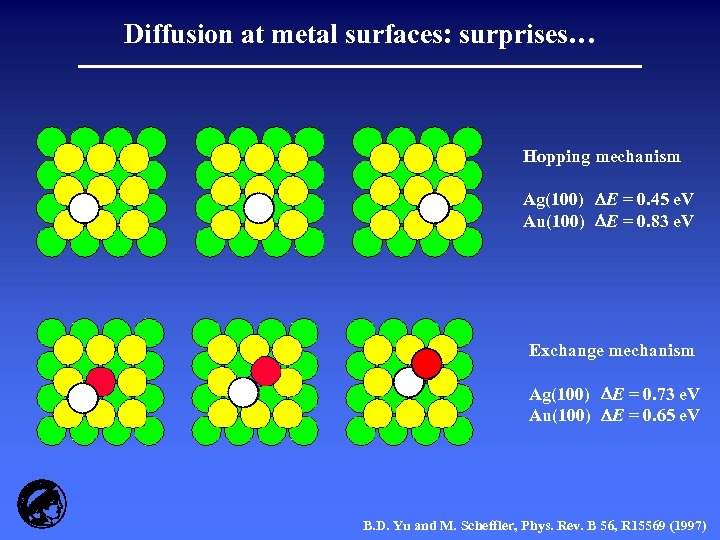
Diffusion at metal surfaces: surprises… Hopping mechanism Ag(100) E = 0. 45 e. V Au(100) E = 0. 83 e. V Exchange mechanism Ag(100) E = 0. 73 e. V Au(100) E = 0. 65 e. V B. D. Yu and M. Scheffler, Phys. Rev. B 56, R 15569 (1997)

Automatized process identification Accelerated molecular dynamics: TAD Hyperdynamics Other approaches: - metadynamics - dimer method …

V. If it works, it works: VI. First-principles k. MC simulations for oxidation catalysis

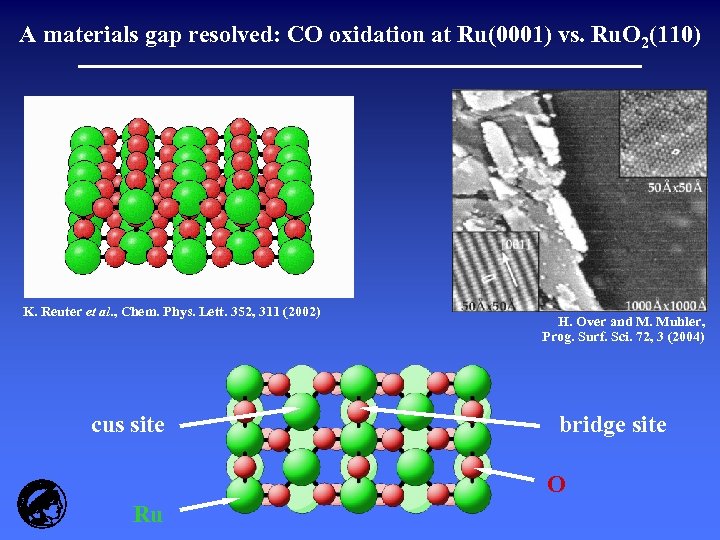
A materials gap resolved: CO oxidation at Ru(0001) vs. Ru. O 2(110) K. Reuter et al. , Chem. Phys. Lett. 352, 311 (2002) cus site H. Over and M. Muhler, Prog. Surf. Sci. 72, 3 (2004) bridge site O Ru

k. MC events for CO oxidation over Ru. O 2(110) Adsorption: CO - unimolecular, O 2 – dissociative no barrier rate given by impingement r ~ So p/(2 mk. T) Desorption: CO – 1 st order, O 2 – 2 nd order out of DFT adsorption well (= barrier) prefactor from detailed balance Diffusion: hops to nearest neighbor sites site and element specific barrier from DFT (TST) prefactor 1012 s-1 (generic) Reaction: site specific immediate desorption, no readsorption barrier from DFT (TST) prefactor from detailed balance 26 elementary processes considered

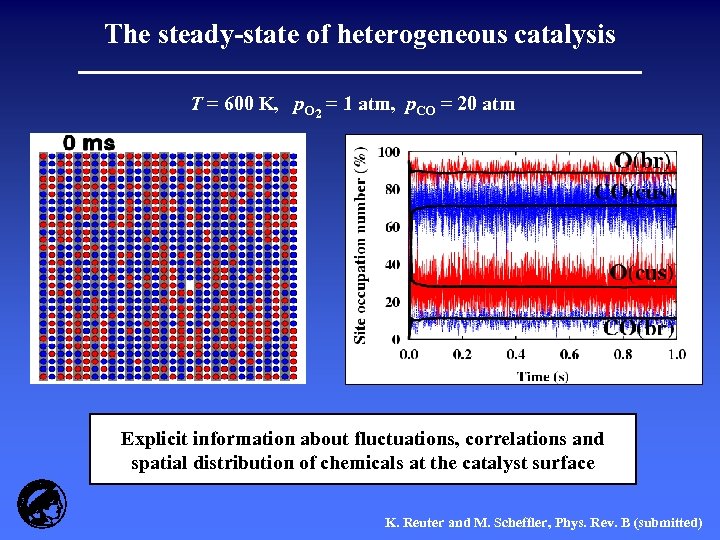
The steady-state of heterogeneous catalysis T = 600 K, p. O 2 = 1 atm, p. CO = 20 atm Explicit information about fluctuations, correlations and spatial distribution of chemicals at the catalyst surface K. Reuter and M. Scheffler, Phys. Rev. B (submitted)

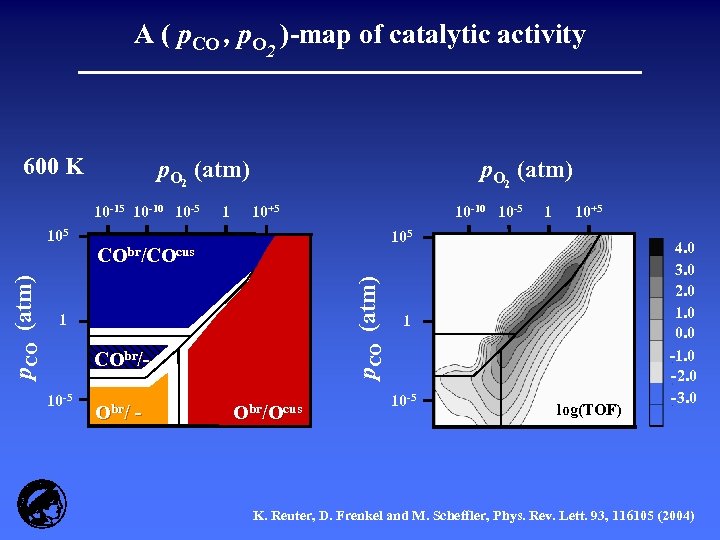
A ( p. CO , p. O 2 )-map of catalytic activity 600 K p. O 2 (atm) 10 -15 10 -10 10 -5 10+5 O /O CObr/ - Obr/Ocus p. CO (atm) ) br /( C O /O ) cus CObr/COcus 1 10 -5 10 -10 10 -5 1 10+5 105 (C p. CO (atm) 105 1 p. O 2 (atm) 1 10 -5 log(TOF) 4. 0 3. 0 2. 0 1. 0 0. 0 -1. 0 -2. 0 -3. 0 K. Reuter, D. Frenkel and M. Scheffler, Phys. Rev. Lett. 93, 116105 (2004)

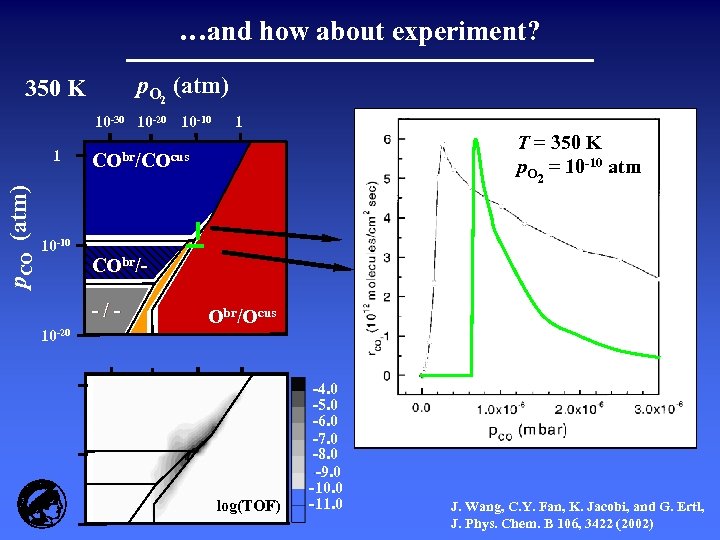
…and how about experiment? p. O 2 (atm) 350 K 10 -30 10 -20 10 -10 p. CO (atm) 1 1 T = 350 K -10 atm pp. O 2 = 10 -10 atm CO = 10 CObr/COcus 10 -10 CObr/-/10 -20 Obr/Ocus log(TOF) -4. 0 -5. 0 -6. 0 -7. 0 -8. 0 -9. 0 -10. 0 -11. 0 J. Wang, C. Y. Fan, K. Jacobi, and G. Ertl, J. Phys. Chem. B 106, 3422 (2002)

Ab initio MD and k. MC simulations Ab initio molecular dynamics: - fully dynamics of the system - straightforward, easy to implement - times scales up to ~ns - acceleration techniques under development Ab initio kinetic Monte Carlo simulations: - coarse-grained time evolution (rare event dynamics) - efficient treatment of statistical interplay of a larger number of elementary processes - time scales given by process rates, often seconds or longer - process list (process identification, lattice models) - accuracy of rates (DFT-TST), high CPU cost - low speed-up, if very fast processes present