86d3b46aab125778df5bff6924747e89.ppt
- Количество слайдов: 47

BOUNDS AND OTHER NO ARBITRAGE CONDITIONS ON OPTIONS PRICES First we review the topics: Risk-free borrowing and lending and Short sales 1

Risk-free lending and borrowing Arbitrage: A market situation in which an investor can make a profit with: no equity and no risk. Efficiency: A market is said to be efficient if prices are such that there exist no arbitrage opportunities. Alternatively, a market is said to be inefficient if prices present arbitrage opportunities for investors in this market. 2

Risk-free lending and borrowing PURE ARBITRAGE PROFIT: A PROFIT MADE 1. WITHOUT EQUITY INVESTMENT and 2. WITHOUT ANY RISK We will assume that the options market is efficient. This assumption implies that one cannot make arbitrage profits in the options markets 3

We are now ready to analyze upper and lower BOUNDS AND OTHER NO ARBITRAGE CONDITIONS ON OPTIONS PRICES. The basic assumptions and notations that underlie the analysis are: 4

ASSUMPTIONS: 1. The market is frictionless: No transaction cost nor taxes exist. Trading are executed instantly. There exists no restrictions to short selling. 2. Market prices are synchronous across assets. If a strategy requires the purchase or sale of several assets in different markets, the prices in these markets are simultaneous. Moreover, No bid-ask spread exist only one market price. 5

ASSUMPTIONS: 3. Risk-free borrowing and lending exists at the unique risk-free rate. Risk-free borrowing and lending is done via selling short and purchasing T-bills 4. There exist no arbitrage opportunities in the options market. 6

NOTATIONS: t = the current date. St = the current market price of the underlying asset. X = the option’s exercise (strike) price. K in the text book. T = the option’s expiration date. T-t = the time remaining to the option’s expiration. r = the annual risk-free rate. = the annual standard deviation of the returns on the underlying asset. D = cash dividend per share. 7

NOTATIONS: Ct = the current market premium of an American call. ct = the current market premium of an European call. Pt = the current market premium of an American call. pt = the current market premium of an European call. In general, we express the options’ premiums as the following functions: Ct , ct = c{St , X, T-t, r, , D }, Pt , pt = p{St , X, T-t, r, , D }. 8

FINAL REMARK: Many strategies described below use lending or borrowing capital at the riskfree rate. Mostly, the amount borrowed or lent is the discounted value of the option’s exercise price. Namely, Xe-r(T-t). The assumption here is that the holder of the strategy can always buy T-bills (lend) or sell short T-bills (borrow) for exactly the amount of Xe-r(T-t). It follows that upon terminating the strategy at the option’s expiration time, the lender will receive this amount’s face value, namely, a cash flow of X. If borrowed, the borrower will pay this amount’s face value, namely, a cash flow of – X. 9

RESULTS FOR CALLS: 1. Call values at expiration: (3. 1) page 102 CT = c. T = Max{ 0, ST – X }. Proof: At expiration the call is either exercised, in which case CF = ST – X, or you let the option expire worthless, in which case, CF = 0. 10

RESULTS FOR CALLS(P 104): 2. Minimum call value: A call premium cannot be negative. At any time t, prior to expiration, Ct , ct 0. Proof: The current market price of a call is the NPV[Max{ 0, ST – X }] 0. 3. Maximum Call value: Ct St. Proof: The call is a right to buy the stock. Investors will not pay for this right a price that is higher than what the value the right to buy gives them, I. e. , the stock itself. 11

RESULTS FOR CALLS: 4. Lower bound: American call value: At any time t, prior to expiration, Ct Max{ 0, St - X}. Proof: Assume to the contrary that Ct < Max{ 0, St - X}. Then, buy the call and immediately exercise it for an arbitrage profit of: St – X – Ct > 0. Contradiction of the no arbitrage profits assumption. 12

RESULTS FOR CALLS: 11. The money value of calls: The higher the exercise price, the lower is the value of a call. Proof: Let X 1 < X 2 be the exercise prices for two calls on the same underlying asset and the same time to expiration. To show that c 2 < c 1 assume, to the contrary, that c 2 > c 1 or, c 2 - c 1 > 0. Then, At expiration Strategy ICF ST < X 1<ST < X 2 ST >X 2 Sell c(X 2 ) c 2 Buy c(X 1 ) -c 1 Total ? 0 0 -(ST –X 2) ST – X 1 X 2 - X 1 In the absence of arbitrage the initial cash 13 flow cannot be positive.

RESULTS FOR CALLS: 12. The money value of calls: Let X 1 < X 2 then C 1 - C 2 X 2 - X 1 Proof: Let X 1 < X 2 be the exercise prices or two American calls on the same underlying asset and the same time to expiration. Assume that C 1 - C 2 > X 2 - X 1 or, equivalently: C 1 - C 2 – (X 2 - X 1) > 0. Then, At expiration Strategy ICF ST < X 1<ST < X 2 ST >X 2 Sell C(X 1 ) C 1 0 -(ST –X 1) Buy C(X 2 )-C 2 0 0 ST–X 2 Lend Total – (X 2 - X 1) X 2 -X 1+i X 2 - X 1+i ? X 2 -X 1+i X 2 -ST+i X 2 - X 1+i i i = interest Even if the sold call is exercised before Expiration, the total value in hand is >0. 14

RESULTS FOR CALLS: 13. The money value of calls: Let X 1<X 2 then c 1 -c 2 (X 2 -X 1)e-r(T-t) Proof: Let X 1 < X 2 for two European calls on the same underlying asset and the same time to expiration. Assume that c 1 -c 2 > (X 2 -X 1)e-r(T-t) or, c 1 -c 2 -(X 2 -X 1)e-r(T-t) >0. Then, At expiration Strategy ICF ST < X 1<ST < X 2 ST >X 2 Sell c(X 1 ) c 1 0 -(ST –X 1) Buy c(X 2 )-c 2 0 0 ST–X 2 Lend -(X 2 -X 1)e-r(T-t) X 2 -X 1 Total ? X 2 -X 1 X 2 - ST 0 In the absence of arbitrage, the initial 15 cash flow cannot be positive.

RESULTS FOR CALLS: 5. Lower bound: European call value: At any time t, prior to expiration, ct Max{ 0, St - Xe-r(T-t)}. Proof: If, to the contrary, ct < Max{ 0, St - Xe-r(T-t)}, then, 0 < St - Xe-r(T-t) - ct At expiration Strategy I. C. F ST < X ST > X Sell stock short St -ST Buy call - ct 0 ST - X Lend funds - Xe-r(T-t) X X Total ? X – ST 0 In the absence of arbitrage, the initial 16 cash flow cannot be positive.

RESULTS FOR CALLS: 6. The market value of an American call is at least as high as the market value of a European call. Ct ct Max{ 0, St - Xe-r(T-t)}. Proof: An American call may be exercised at any time, t, prior to expiration, t<T, while the European call holder may exercise it only at expiration. 17

RESULTS FOR CALLS: 7. The time value of calls: The longer the time to expiration, the higher is the value of a call. Proof: Let T 1 < T 2 for two calls on the same underlying asset and the same exercise price. To show that c 2 > c 1 assume, to the contrary, that c 1 > c 2 or, c 1 - c 2 > 0. At expiration T 1 Strategy I. C. F ST 1 < X ST 1 > X Sell c(T 1 ) c 1 0 -(ST 1 –X) Buy c(T 2 ) - c 2 c(TV) C(T 2 -T 1) Total ? c(TV) ? 18

RESULTS FOR CALLS: Case 1. The calls are American style. The question is whether C(T 2 -T 1) - (ST 1 –X) ? If > 0 the proof is completed. If < 0, the open call can be exercised immediately for (ST 1 –X) and the proof is complete. Case 2. The calls are European style. In this case, result 5. Guarantees that the cash flow above is >0 because ct 1 St 1 - Xe-r(T 2 -T 1). 19

RESULTS FOR CALLS: 8. Cash dividends and calls: It is not optimal to exercise an American call prior to its expiration if the underlying stock does not pay out any dividend during the life of the option. Proof: If an American call holder wishes to rid of the option at any time prior to its expiration, the market premium is greater than the intrinsic value because the time value is always positive. 9. The American feature is worthless if the underlying stock does not pay out any dividend during the life of the call. Mathematically: Ct = ct. Proof: Follows from result 8. above. 20

RESULTS FOR CALLS: 10. Early exercise of Unprotected American calls on a cash dividend paying stock. (Section 8. 7): Consider an American call on a cash dividend paying stock. It may be optimal to exercise this American call an instant before the stock goes X dividend. Two condition must hold for the early exercise to be optimal: First, the call must be in-the-money. Second, the $[dividend/share], D, must exceed the time value of the call at the x dividend instant. To see this result Consider: 21

RESULTS FOR CALLS: FACTS: 1. The share price drops by $D/share when the stock goes x-dividend. 2. The call value decreases when the price per share falls. 3. The exchanges do not compensate call holders for the loss of value that ensues the price drop on the xdividend date. t 4. S CUMD A S t XDIV t =S XDIV PAYMENT CDIV Time line - D. 22

Early exercise of Unprotected American calls on a cash dividend paying stock: The call holder goal is to maximize the Cash flow from the call. Thus, at any moment in time, exercising the call is inferior to selling the call. This conclusion may change, however, an instant before the stock goes x dividend: Exercise Cash flow: Do not exercise SCD – X; c{SXD, X, T-t. XD-} SCD = SXD + D. Cash flow: SXD –X + D; SXD – X + TV. Substitute: Conclusion: Early exercise of American calls may be optimal. If the call is in the money and D > TV, early exercise is optimal. 23

Early exercise of Unprotected American calls on a cash dividend paying stock: This result means that an investor is indifferent to exercising the call an instant before the stock goes x dividend if the x dividend stock price S*XD satisfies: S*XD –X + D = c{S*XD , X, t. XD-t}. It can be shown that this implies S*XD exists if: D > X[1 – e-r(T – t)]. that the price 24

RESULTS FOR CALLS: 14. The money value of calls: Let X 1 < X 2 < X 3 and X 2 = X 1 + (1 - )X 3 for 0 < < 1. The premiums on the three calls must satisfy: c 2 c 1 + (1 - )c 3 At Expiration STRATEGY ICF ST < X 1<ST < X 2 <ST < X 3 Buy calls X 1 - c 1 0 Sell one call X 2 c 2 0 Buy 1 - calls X 3 -(1 - )c 3 0 Total c 2 - c 1 -(1 - )c 3 0 ST > X 3 (ST – X 1) 0 -(ST – X 2) 0 0 (1 - )(ST–X 3) (ST–X 1) (1 - )(X 3 -ST) 0 All the cash flows at expiration are non negative. Hence, the Initial Cash Flow cannot be positive! I. e. , c 2 - c 1 -(1 - )c 3 0. Or, c 2 c 1 + (1 - )c 3. Remark: When = 1/2 , the strategy is called a Butterfly. In this case, 2 X 2 = X 1 + X 3 and the result asserts: 2 c 2 c 1 + c 3 25

RESULTS FOR CALLS: Example: Let $80, $95 and $100 be the exercise prices of three calls on the same underlying asset and the same expiration. Observe that: $95 = (. 25)$80 + (. 75)$100. Thus, in this case, = ¼. Result 14. Asserts that c(95) ¼c(80) + ¾c(100). Or, 4 c(95) c(80) + 3 c(100). If the latter inequality does not hold, then 4 c(95) > c(80) + 3 c(100) or, 4 c(95) - c(80) - 3 c(100) > 0 and arbitrage profit can be made by the Strategy: Buy the $80 call Sell four $95 calls Buy three $100 calls. 26

RESULTS FOR CALLS: 15. Volatility: The higher the price volatility of the Underlying asset, the higher is the Call value. Proof: The call holder never loses more than the initial premium. The upside gain, however, is unlimited. Thus, higher volatility increases the potential gain while the potential loss remains Unchanged. 27

RESULTS FOR CALLS: 16. The interest rate: The Higher the risk-free rate, the Higher is the call value. Proof: The result follows from result 6: Ct ct Max{ 0, St - Xe-r(T-t)}. With increasing risk-free rates, the difference St - Xe-r(T-t) increases and the call value must increase as well. 28

RESULTS FOR PUTS: 17. Put values at expiration: PT = p. T = Max{ 0, X - ST}. Proof: At expiration the put is either exercised, in which case CF = X - ST, or it is left to expire worthless, in which case CF = 0. 29

RESULTS FOR PUTS: 18. Minimum put value: A put premium cannot be negative. At any time t, prior to expiration Pt , pt 0. Proof: The current market price of a put is the NPV[Max{ 0, X - ST}] 0. 19 a. Maximum American Put value: At any time t < T, Pt X. Proof: The put is a right to sell the stock for X, thus, the put’s price cannot exceed the maximum value it will create: X, which occurs if S drops to zero. 30

RESULTS FOR PUTS: 19 b. Maximum European Put value: Pt Xe-r(T-t). Proof: The European put may be exercised only at expiration. The maximum revenue it can create at that time is X, ( in case S drops to zero), thus, at any time point before expiration, the European put cannot exceed the NPV{X}. 31

RESULTS FOR PUTS: 20. Lower bound: American put value: At any time t, prior to expiration, Pt Max{ 0, X - St}. Proof: Assume to the contrary that Pt < Max{ 0, X - St}. Then, buy the put and immediately exercise it for an arbitrage profit of: X - St – Pt > 0. A contradiction of the no arbitrage profits assumption. 32

RESULTS FOR PUTS(P 116): 21. Lower bound: European put value: At any time t, t < T, pt Max{ 0, Xe-r(T-t) - St}. Proof: If, to the contrary, pt < Max{ 0, Xe-r(T-t) - St} then, 0 < Xe-r(T-t) - St - pt At expiration Strategy I. C. F ST < X ST > X Buy stock -St ST ST Buy put - pt X - ST 0 Borrow Xe-r(T-t) - X -X Total ? 0 ST - X In the absence of arbitrage, the initial cash flow cannot be positive. 33

RESULTS FOR PUTS: 22. The market value of an American put is at least as high as the market value of a European put. Pt pt Max{0, Xe-r(T-t) - St}. Proof: An American put may be exercised at any time, t, prior to expiration, t<T, while the European put holder may exercise it only at expiration. 34

RESULTS FOR PUTS: 23. The time value of puts: The longer the time to expiration, the higher is the value of an American put. Proof: Let T 1 < T 2 for two American puts on the same underlying asset and the same exercise price. To show that P 2 > P 1 assume, to the contrary, that P 1 > P 2 or, P 1 - P 2 > 0. At expiration T 1 Strategy I. C. F ST 1 < X Sell P(T 1 ) P 1 -(ST 1 –X) 0 Buy P(T 2 ) -P 2 P(T 2 -T 1) P(TV) Total ? ? P(TV) You may exercise the put. The result follows. 35

RESULTS FOR PUTS: 24. American put is always priced higher than its European counterpart. Pt p t Proof: An American put may be exercised at any time, t, prior to expiration, t<T, while the European put holder may exercise it only at expiration. Moreover, if The price of the underlying asset fall below a certain threshold price, it becomes Optimal to exercise the American put and earn X – St. At that very same moment the European put holder wants to (optimally) Exercise the put but cannot because it is a European put. The next figure demonstrates the relationship Between the American and European puts premiums. 36
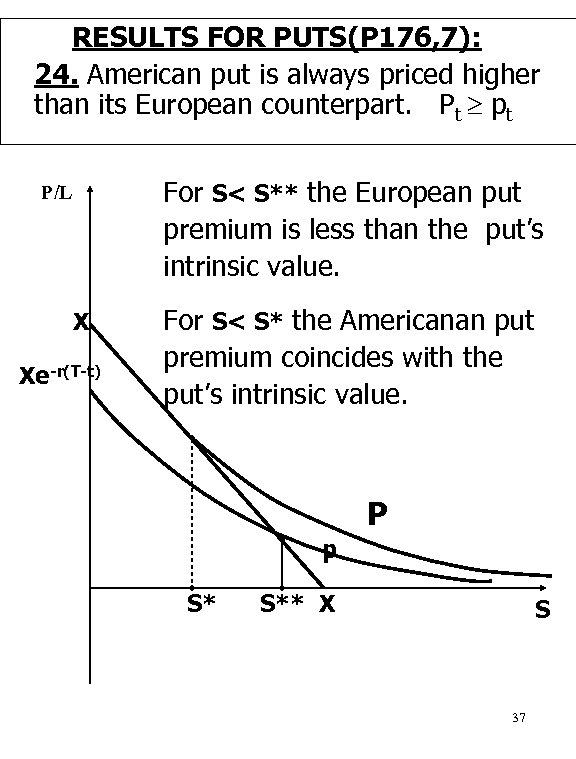
RESULTS FOR PUTS(P 176, 7): 24. American put is always priced higher than its European counterpart. Pt pt For S< S** the European put premium is less than the put’s intrinsic value. P/L X Xe-r(T-t) For S< S* the Americanan put premium coincides with the put’s intrinsic value. P p S* S** X S 37

RESULTS FOR PUTS: 25. The money value of puts: The higher the exercise price, the higher is the value of a put. Proof: Let X 1 < X 2 for two puts on the same underlying asset and the same time to expiration. To show that p 2 > p 1 assume, to the contrary, that p 2 < p 1 or, p 1 - p 2 > 0. Then, At expiration Strategy ICF ST < X 1<ST < X 2 ST >X 2 Sell p(X 1 ) p 1 ST –X 1 Buy p(X 2 ) -p 2 X 2 –ST Total ? X 2 - X 1 0 X 2 - ST 0 In the absence of arbitrage, the initial cash flow cannot be positive. 38

RESULTS FOR PUTS: 26. The money value of puts: Let X 1 < X 2 then P 2 - P 1 X 2 - X 1 Proof: Let X 1 < X 2 be the exercise prices or two American puts on the same underlying asset and the same time to expiration. Assume that P 2 - P 1 > X 2 - X 1 or, equivalently: P 2 - P 1 – (X 2 - X 1) > 0. Then, At expiration Strategy ICF ST < X 1<ST < X 2 ST >X 2 Sell P(X 2 ) P 2 ST –X 2) 0 Buy P(X 1 )-P 1 X 1 – S T 0 0 Lend Total – (X 2 - X 1) ? X 2 -X 1+i X 2 - X 1+i i ST-X 1 +i X 2 - X 1+i i = interest Even if the sold put is exercised before expiration, the total value in hand is >0. 39

RESULTS FOR PUTS: 27. The money value of puts: Let X 1<X 2 then p 2 -p 1 (X 2 -X 1)e-r(T-t) Proof: Let X 1 < X 2 for two European puts on the same underlying asset and the same time to expiration. Assume that p 2 -p 1 > (X 2 -X 1)e-r(T-t) or, p 2 - p 1 -(X 2 -X 1)e-r(T-t) >0. Then, At expiration Strategy ICF ST < X 1<ST < X 2 ST > X 2 Sell p(X 2 ) p 2 ST –X 2 0 Buy p(X 1 )-p 1 X 1 – S T 0 0 Lend -(X 2 -X 1)e-r(T-t) X 2 -X 1 Total ? 0 X 2 - ST X 2 -X 1 In the absence of arbitrage, the initial 40 cash flow cannot be positive.

RESULTS FOR PUTS: 28. Volatility: The higher the price volatility of the underlying asset, the higher is the put value. Proof: The put holder never loses more than the initial premium. The upside gain, however, is increasing from zero to X. Thus, higher volatility increases the potential gain while the potential loss remains Unchanged. 41

RESULTS FOR PUTS: 29. The interest rate: The higher the risk-free rate, the lower is the put value. Proof: Follows from result 22: Ct ct Max{ 0, Xe-r(T-t) -St}. With increasing risk-free rates, the difference Xe-r(T-t) - St decreases and the put value decrease too. 42

RESULTS for PUTS and CALLS: (Section 8. 4) 30. The put-call parity. European options: The premiums of European calls and puts written on the same non dividend paying stock for the same expiration must satisfy: ct - pt = St - Xe-r(T-t). The parity may be rewritten as: ct + Xe-r(T-t) = St + pt. Below, we prove the latter version of the parity. 43

RESULTS for PUTS and CALLS: Proof. Consider the following two portfolios: A: Long the stock and the put. B: Long the call and lend Xe-r(T-t). Portfolio A: At expiration Strategy I. C. F ST < X ST > X Buy stock -St ST ST Buy put - pt X - ST 0 Total -(St+pt) X ST Portfolio B: At expiration Strategy I. C. F ST < X ST > X Buy call - ct 0 ST-X Lend - Xe-r(T-t) X X Total -(ct+ Xe-r(T-t) ) X ST Portfolios A and B have identical cash flows At expiration for all possible prices. Thus, their initial values are equal: ct + Xe-r(T-t) = St + pt. 44

RESULTS for PUTS and CALLS: 31. Synthetic European options: The put-call parity ct - pt = St - Xe-r(T-t) can be rewritten as a synthetic call: ct = pt + St - Xe-r(T-t), Or as a synthetic put: pt = ct - St + Xe-r(T-t). Observe that the parity implies that at-themoney calls are priced higher than their counterpart puts. For at-the-money options, ct = pt + St - Xe-r(T-t) becomes: ct = pt + X - Xe-r(T-t) > pt. 45

RESULTS for PUTS and CALLS: 32. The put-call parity. European options: Suppose that European puts and calls are written on a dividend paying stock and suppose that there will be two dividend Payments: D 1 at t 1 and D 2 at t 2. The option’s premiums must satisfy the following equation: ct-pt = St-Xe-r(T-t) – D 1 e-r(t 1 -t) – D 2 e-r(t 2 -t) The proof follows the same path of result 30. But the stock will pay dividend twice at t 1 and t 2. Thus, borrowing the discounted value of the dividends and paying them upon receiving the dividends will leave the strategy unaffected and the result follows. 46

RESULTS for PUTS and CALLS: 34. The put-call parity. American options: The put-call parity for European options asserts that: ct - pt = St - Xe-r(T-t). This result does not necessarily hold for American options. The premiums on American options satisfy the following inequalities: St - X < Ct - Pt < St - Xe-r(T-t). 47
86d3b46aab125778df5bff6924747e89.ppt