Born-Oppenheimer Coupling Terms as Molecular Fields Michael Baer

Born-Oppenheimer Coupling Terms as Molecular Fields Michael Baer The Fritz Haber Research Center for Molecular Dynamics, The Hebrew University of Jerusalem, Israel

Colleagues – Past & Present n Longstanding Collaborations n Prof. G. D. Billing (deceased) Prof. A. Vibok (Debrecen, Hungary) Prof. G. J. Halasz (Debrecen, Hungary) Prof. R. Englman (Soreq, Israel) Prof. A. M. Mebel (Intl. Univ. Miami, Fl USA) Prof. S. Adhikari (ITT, Guwahati, India) Mr. B. Sarkar, (ITT, Guwahati, India) Dr. T. Vertesi (Debrecen, Hungary) Prof, D. J. Kouri, (Houston, TX, USA) Prof. D. K. Hoffman (Ames, IA, USA) Prof. R. Baer (Jerusalem, Israel) n n n Short Collaborations n Prof. A. Alijah (Coimbra, Portugal) Dr. E. Bene (Debrecen, Hungary) Dr. A. Yahalom (Ariel, Israel) Dr. S. Hu (Houston, TX, USA) Prof. A. J. C. Varandas (Coimbra, Portugal) Dr. Z. R. Xu (Coimbra, Portugal) Dr. D. Charutz (Soreq, Israel) Prof. R. Kosloff (Jerusalem, Israel) Prof. J. Avery (Copenhagen, Denmark) Prof. S. H. Lin (IAMS, Taipei, Taiwan) n n n n n 2

Introduction The Non-adiabatic Coupling Term as a Physical Entity

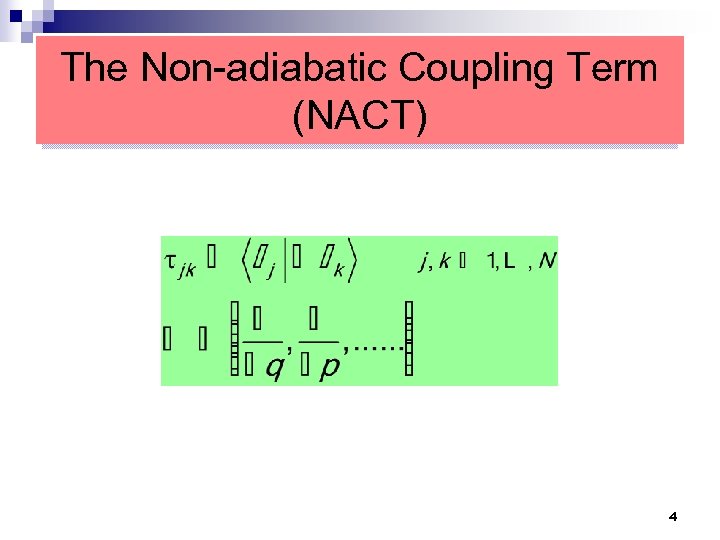
The Non-adiabatic Coupling Term (NACT) 4

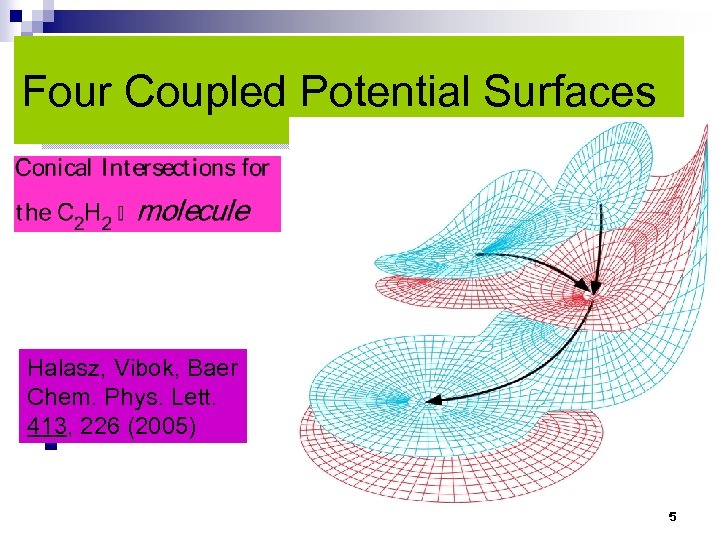
Four Coupled Potential Surfaces Halasz, Vibok, Baer Chem. Phys. Lett. 413, 226 (2005) n 5

What is the Purpose of this Lecture? n To understand the physical contents of the NACTs n By Definition a NACT is a vector but…. ? n We show that NACTs behave like fields 6

Contents n I. The Hilbert Space n II. Degeneracy Points as Poles n III. Vector Algebra to Form Two-state (Quantum) fields n IV. Field Equations to Form Multi-State (Quantum) Fields 7

Chapter I The Hilbert Space

Introduction n Consider a series of N-dimensional Hilbert spaces n Resolution of unity: 9

The NACT n The connection between the Hilbert spaces of adjacent points is described in terms of an Nx. N vectorial matrix: is the electronic Born Oppenheimer NACT matrix n is an anti-symmetric matrix n 10

Connecting Hilbert Spaces n Two Hilbert spaces at nearby points: n Recalling the resolution of the unity (and multiplying by ) 11

We obtain: n Solving the First order Differential R. Baer, J. n The. Phys. 117, 405 (2002). a prescribed contour Chem. Integration is along 12

Closed Contour sf si n For a closed contour (loop) n In loops: return to the same state (up to phase) A. Alijah and M. Baer, Chem. Phys. Lett. 319, 489 (2000) 13

Quantization Conditions n A group of N states forms a Hilbert space (in a given region) if and only if the D-matrices are diagonal along any contour : 14

Quantization Conditions n In the case of real eigenfunctions: n In case of two states (N=2): the D-matrix can be written as: A. Alijah and M. Baer, Chem. Phys. Lett. 319, 489(2000) 15

Bohr-Sommerfeld Quantization n Condition The 2 2 D( )-matrix becomes diagonal if: 16

Hilbert subspace n We assume that breaks up into blocks n 17

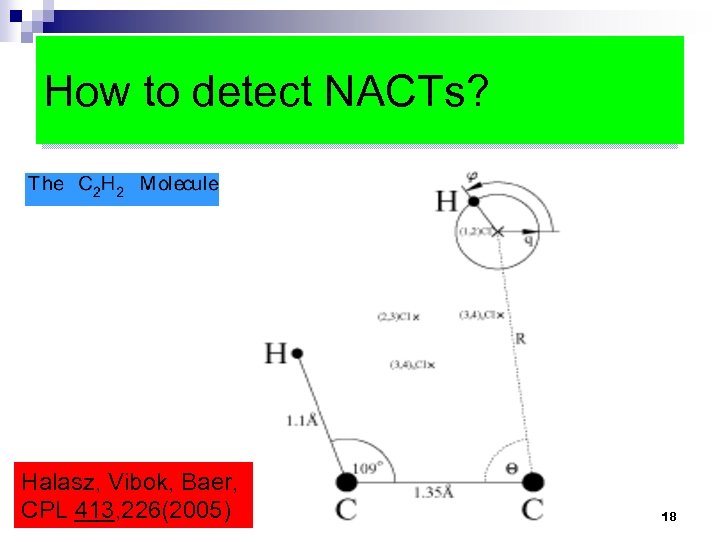
How to detect NACTs? Halasz, Vibok, Baer, CPL 413, 226(2005) 18

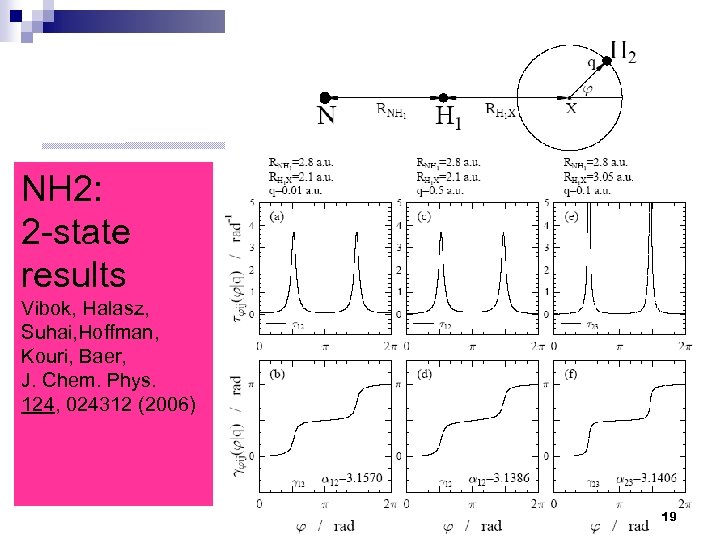
NH 2: 2 -state results Vibok, Halasz, Suhai, Hoffman, Kouri, Baer, J. Chem. Phys. 124, 024312 (2006) 19

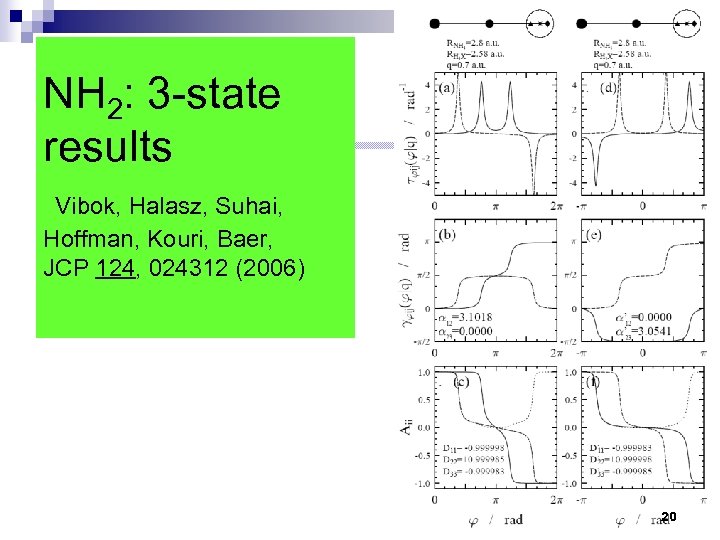
NH 2: 3 -state results Vibok, Halasz, Suhai, Hoffman, Kouri, Baer, JCP 124, 024312 (2006) 20

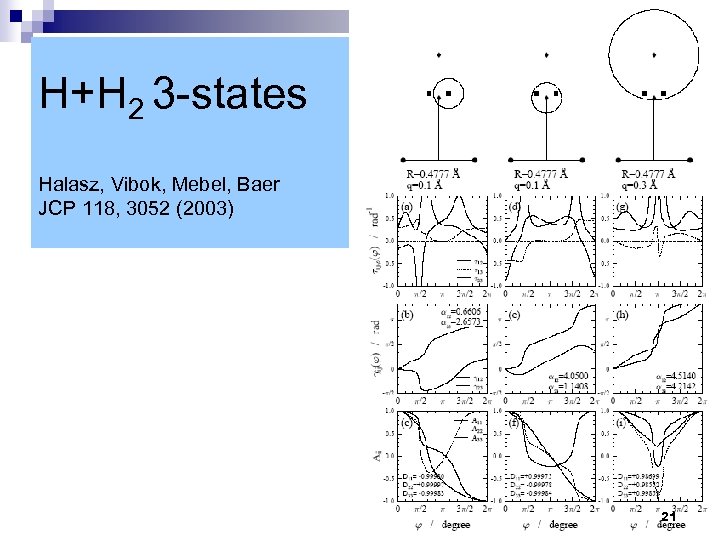
H+H 2 3 -states Halasz, Vibok, Mebel, Baer JCP 118, 3052 (2003) 21

The Curl Equation n The eigenfunctions of a Hilbert space satisfy, for any (p, q) tensorial component, the equality : n This equality is termed as the Curl Condition n If the NACT-matrix breaks up into blocks the Curl Condition is fulfilled for each Block M. Baer, Chem. Phys. Lett. 35, 112 (1975) 22

The Curl Equation (continued) n Abelian vs non-Abelian variables n Commutation Relation ¨ The -matrix is, in general, non-Abelian ¨A 2 2 -matrix is Abelian 23

The curl condition for Two-state System: n Here: n This case is Abelian and therefore: j CI n q In polar coordinates 24

The Divergence Equation n The eigenfunctions of a Hilbert space form also a Divergence equation n where n In polar coordinates: j CI q 25

Div (s) for a Two-State System n In Cartesian Coordinates n The (2) matrix elements are: n In contrast to -matrix elements, they are scalars 26

Chapter II Degeneracy Points As Poles

The Degeneracy Point and its Close Vicinity n At the vicinity of DP the corresponding NACT behaves like a Pole: it is singular and decays like (1/q) n At the vicinity of DP the corresponding NACT possesses an angular component. n At the vicinity of DP the radial component of the corresponding NACT is negligible small. n At the vicinity of DP related to a given NACT the effect of all other NACTs is negligible small 28

The Epstein Theorem n The Epstein Theorem States that (at every point in CS): n Degeneracy Points (DP) can only be formed if 29

The Epstein Theorem at Degeneracy Points n At the vicinity of a DP we consider the angular component: CI n j q At the vicinity of a DP we expand for q~0 30

The Pole and the Quantization n For the DP to be a Pole: n In such a case: n Recalling Quantization (Berry Phase): 31

Stokes Theorem n j The (Abelian) 2 2 Curl Condition: q CI S ¨ There is an unresolved issue at q=0: We have to define F at q=0 to fulfill Stokes Theorem. n Stokes theorem Asserts that: M. Maer, Chem. Phys. Lett. 349, 149 (2001) Vertesi, Vibok, Halasz, Yahalom, Englman and Baer, J. Phys. Chem. A 107, 7189 32

Stokes Theorem (Cont. ) n The line integral Fulfills Bohr-Sommerfeld Quantization law n F has to be extended to have a value at the DP point: n To fulfill the Stokes Theorem must obey 33

Close vicinity of DP (Example: solving the Curl Equation) n Having the Curl equation n We derive the angular component of : n Thus near a DP (q 0): Will be taken as boundary values around each DP 34

35

The Angular NACT for H+H 2 36

Summary (what did we achieve so far? ) n The Curl-Div Equations fulfilled by the NACTs can be applied to derive the related fields (just like the Maxwell Equations are applied to calculate the electro-magnetic fields) n The boundary conditions needed to calculate these fields are formed at the close vicinity of the DPs and are obtained from Ab-initio calculations using given packages (MOLPRO). 37

Chapter III Vector Algebra to Form Two-State Quantum Fields

Vector Algebra for Abelian Systems n Expression for a single ci as seen from a given origin n Where: 39

For Several DPs n The NACT field formed at N DPs: J. Avery, M. Baer and G. D. Billing, Molec. Phys. 100, 1011 (2002) 40

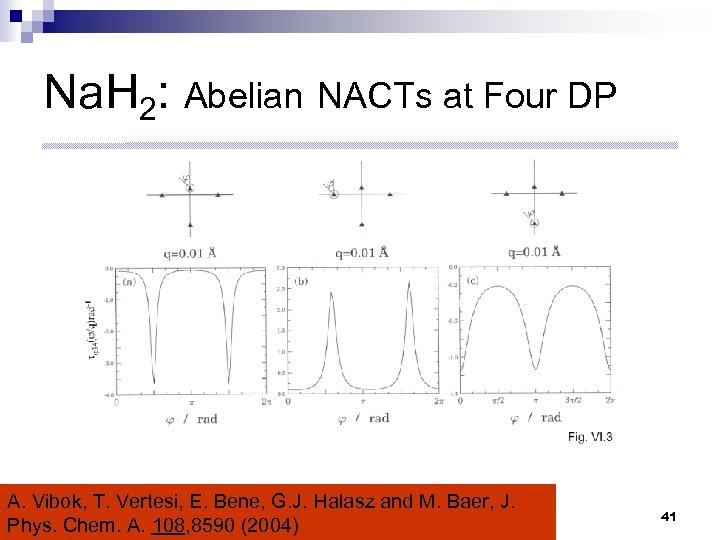
Na. H 2: Abelian NACTs at Four DP A. Vibok, T. Vertesi, E. Bene, G. J. Halasz and M. Baer, J. Phys. Chem. A. 108, 8590 (2004) 41

Ab-initio vs. Vector Algebra (Na. H 2) as calculated along four different contours Vibok, Vertesi, Bene, Halasz, Baer, J. Phys. Chem. A 108, 8590 (2004) 42

Chapter IV Field Equations to Form Multi-State Quantum Fields

Field Theory to derive NACTs n The Born-Oppenheimer NACTs are: ¨ ¨ n Vector-fields formed by sources located at DPs. Treated theoretically (and numerically) employing field theory. Methodology: ¨ Calculate Abelian NACTs, jj+1 formed, by states j and j+1, due to a single DP along a small contour surrounding this (j, j+1) DP (e. g. MOLPRO). ¨ At larger regions, due to the existence of DPs formed by other states, the system becomes non-Abelian ¨ The N N -matrix which fulfills the non-Abelian Curl-Equation and the non. Abelian Div-Equation is obtained by solving these equations. ¨ This calculated matrix contains the non-Abelian Quantum Fields. 44

The Curl Equation for a 3 -state System M. Baer, A. M. Mebel and G. D. Billing, Int. J. Quant. Chem. 90, 1577 (2002) 45

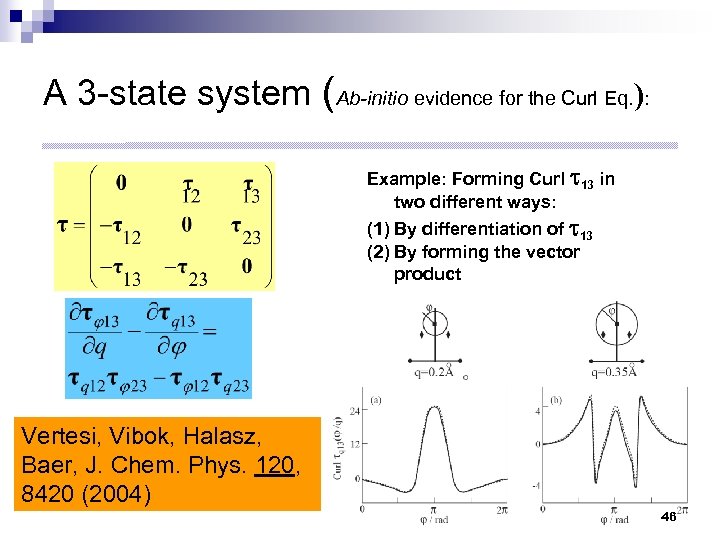
A 3 -state system (Ab-initio evidence for the Curl Eq. ): Example: Forming Curl 13 in two different ways: (1) By differentiation of 13 (2) By forming the vector product Vertesi, Vibok, Halasz, Baer, J. Chem. Phys. 120, 8420 (2004) 46

The Div-Equation for a 3 -state System Vertesi, Vibok, Halasz, M. Baer, J. Chem. Phys. 121, 4000 (2004 ) 47

The Poisson Equations n Curl-Div Equations for each one of the NACTs: n Decoupling of the two components Vertesi, Vibok, Halasz, Baer, J. Chem. Phys. 121, 4000 (2004) 48

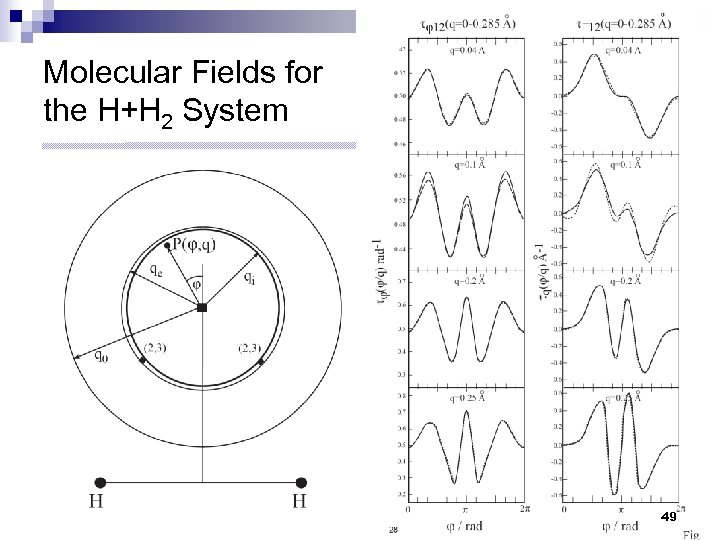
Molecular Fields for the H+H 2 System 49

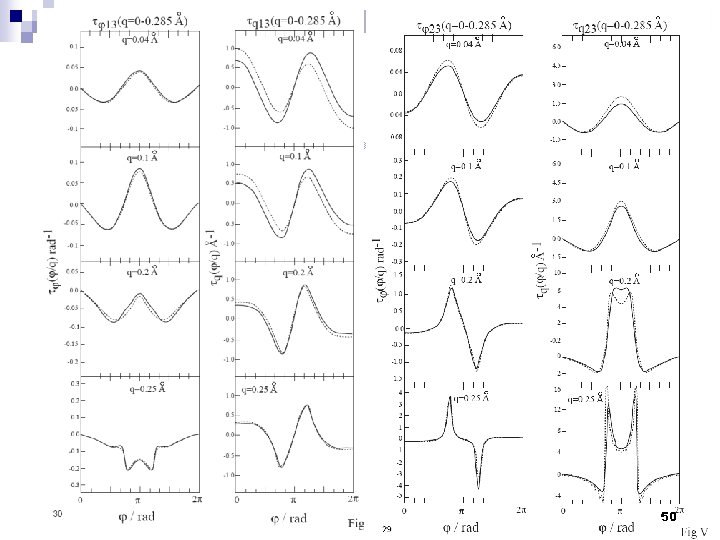
50

Summary n n n We showed that NACTs are created at degeneracy points and their spatial distribution can be derived by solving Maxwell Equations. Consequently the NACTs are fields and we suggest to call them Quantum Fields. It is not clear if these fields are related to the electromagnetic fields but, if so, they should be termed as Weak Electro-Magnetic Fields. 51

52