814a18b1c04aca05ec7d6541c53dc841.ppt
- Количество слайдов: 13

Boosting an old method with a new basis: MP 2 electron correlation Andrea Sanfilippo, X. Ren, P. Rinke, V. Blum, K. Reuter, M. Scheffler Fritz-Haber Institut der Max-Planck Gesellschaft
About me… Andrea Sanfilippo 2004 Degree in Material Science at the Milano-Bicocca University Thesis project: Construction of an ab-initio Green function code for non-periodical systems using an Embedding Method (supervised by Trioni, Brivio) 2005/ 2006 Doctoral project at the University College of London: Hybrid computational method for scattering of elastic waves in Metal Matrix Composites Since January 2007 at the at Fritz-Haber Institut in Berlin: Ph. D on ab-initio study of Surface Molecular networks

Introducing Electronic Structure Theory Modern ab-initio methods in the Born-Oppenheimer approximation: n i. ii. n n wave function (Hartree-Fock, post-HF, QM) density functional methods (DFT) Present day DFT functionals and wave function based methods treat accurately bonded systems like metals, semiconductors, molecules… but…in nature weak interactions are widespread (physisorption, protein folding, glues etc. ) How do we treat their ground states accurately and efficiently?

DFT in brief , the Kohn-Sham trick ? Exact Exc unknow, is guessed (often parametrized) i. local (TF, LDA): local density of homogenous and isotropic electron gas approximation ii. semi-local (GGAs): gradient expansions on LDA iii. non-local (OEP, Hy. Fs, vd. W): hybrid density/w. f. to recover long-range physical effects n There is not (yet) a systematic way to treat weak bonded systems n Computationally fast ~ O(N 3), N number of basis E : Ground state energy, TS : Kinetic energy of the free electrons, VII : Nuclear interactions n

The grand-father method of quantum chemistry : Hartree-Fock (1930) n Hartree-Fock approximation n approximation: only Pauli principle considered, but it is a poor approximation, what is missing is called correlation e- dig a hole around himself (like exact solution) n e- e- : Fermi energy, V : Coulomb potential, n : density, VH Hartree potential

Perturbation theory: MP 2 (1934) n The second order of perturbation is a first estimation of correlation between two particles n Computation expensive ~ O(N 5): Basis set to expand MO: n i. ii. n terms Gaussian or Slater type basis set Numerical Atomic Orbitals (NAO) Gaussian generally used so far, to make it faster N : number of atomic basis functions, i, j : molecular orbitals label (spin included)

Two basis set in comparison n § Gaussian: i. Localize basis set ii. Analytical integrals iii. Many functions required to recover physics iv. Construction problematic for heavier elements Numerical atomic orbitals i. Localized basis set ii. Numerical integration iii. Correct physics recovered few functions! iv. Can be more easily generated
Aim of the project n n n Implementation of second order many body perturbation theory using numerical atomic orbital code using Describe weak bonded systems efficiently with the highest accuracy Applications: weak molecular bonds, extended systems in presence of heavy elements, surface physisorption

To improve scaling and timing n Resolution of identity defined as projector giving a computationally cheaper term n In density fitting we introduce an auxiliary basis set the residual depending on the metric. can be minimized Vahtras, Almlof, Feyereiesen (1993). Mulliken notation applied :

Main Features of RI/DF-MP 2 n n Auxiliary basis set taken generally as m ~ N Number of calculations ~ O(m. N 4), but computing time <10% than full-MP 2 and storage can be reduced to ~ O(m. N 2) RI-MP 2 size consistent Resulting error lower than the basis set error (error due to incompleteness of basis set, i. e. BSSE) Weigend et al. (2002), Weigend (2006) , Sodt et al. (2006)

What we have done so far… n n RI-MP 2 is feasible with NAO Development of parallel RI-MP 2 and BSSE correction using a NAO in-house code, “FHI-aims” Basis set study starting from MP 2 or DFT-LDA Applied to small molecules and Hydrogen bonded system with accurate results … and future further optimizations (matrix sparsity, PB …) and application to a wider range of practical systems, adsorption on surfaces in particular The FHI Ab Initio Molecular Sim. (aims) project, www. fhiberlin. mpg. de/aims/
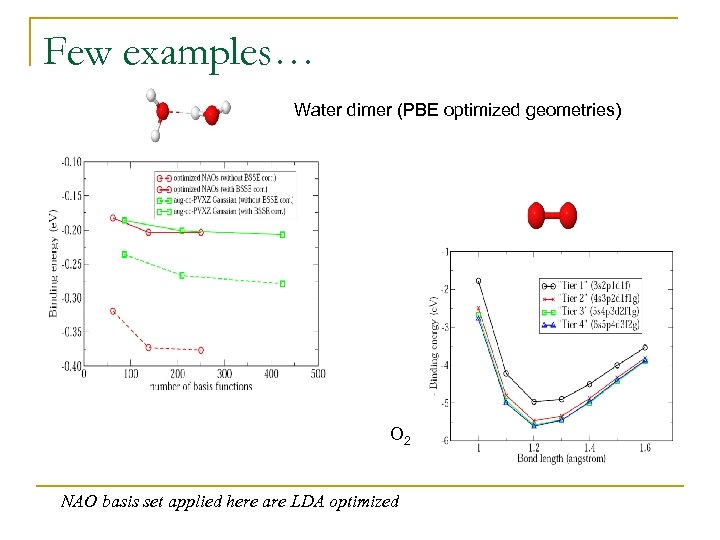
Few examples… Water dimer (PBE optimized geometries) O 2 NAO basis set applied here are LDA optimized

Thanks! Aknowledgements: MONET - Molecular Networks at Phase Boundaries Marie Curie Early Stage Researcher Training Network The FHI Ab Initio Molecular Simulations (aims) project V. Blum and M. Scheffler; R. Gehrke, P. Havu, V. Havu, X. Ren, A. Sanfilippo, F. Hanke, A. Tkatchenko, P. Rinke, and K. Reuter. www. fhiberlin. mpg. de/aims/
814a18b1c04aca05ec7d6541c53dc841.ppt