Boosted Sampling Approximation Algorithms for Stochastic Problems Martin

Boosted Sampling: Approximation Algorithms for Stochastic Problems Martin Pál Joint work with Anupam Gupta R. Ravi Amitabh Sinha TAM 5. 1. '05 Boosted Sampling 1

Anctarticast, Inc. TAM 5. 1. '05 Boosted Sampling 2

Optimization Problem: Build a solution Sol of minimal cost, so that every user is satisfied. minimize cost(Sol) subject to happy(j, Sol) for j=1, 2, …, n For example, Steiner tree: Sol: set of links to build happy(j, Sol) iff there is a path from terminal j to root cost(Sol) = e Sol ce TAM 5. 1. '05 Boosted Sampling 3

Unknown demand? ? ? ? TAM 5. 1. '05 ? Boosted Sampling ? 4

The model Two stage stochastic model with recourse: On Monday, links are cheap, but we do not know how many/which clients will show up. We can buy some links. drawn from a known distribution π On Tuesday, clients appear. Links are now σ times more expensive. We have to buy enough links to satisfy all clients. TAM 5. 1. '05 Boosted Sampling 5

The model Two stage stochastic model with recourse: Want compact representation of Sol 2 by an algorithm Find Sol 1 Edges and Sol 2 : 2 Users 2 Edges to minimize cost(Sol 1) + σ Eπ(T)[cost(Sol 2(T))] subject to happy(j, Sol 1 Sol 2(T)) for all sets T Users and all j T TAM 5. 1. '05 Boosted Sampling 6

What distribution? • Scenario model: There are k sets of users – scenarios; each scenario Ti has probability pi. (e. g. [Ravi & Sinha 03]) • Independent decisions model: each client j appears with prob. pj independently of others (e. g. [Immorlica et al 04]) • Oracle model: at our request, an oracle gives us a sample T; each set T can have probability p. T. [Our work]. TAM 5. 1. '05 Boosted Sampling 7

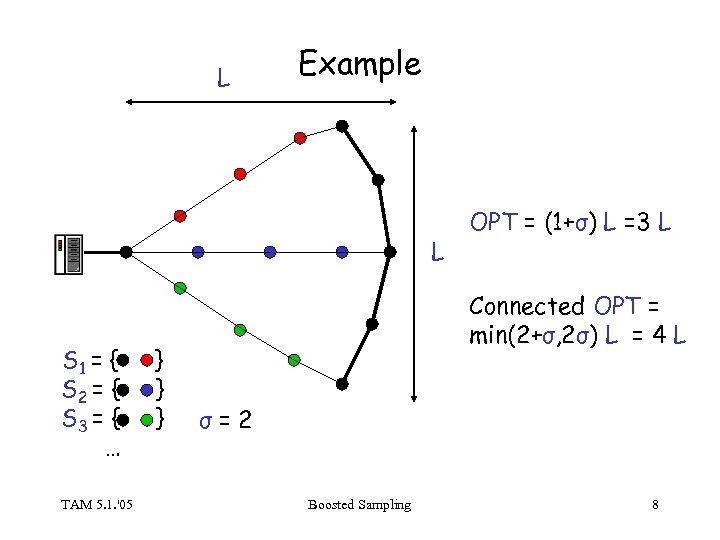
L Example L S 1 = { S 2 = { S 3 = { … TAM 5. 1. '05 } } } OPT = (1+σ) L =3 L Connected OPT = min(2+σ, 2σ) L = 4 L σ=2 Boosted Sampling 8

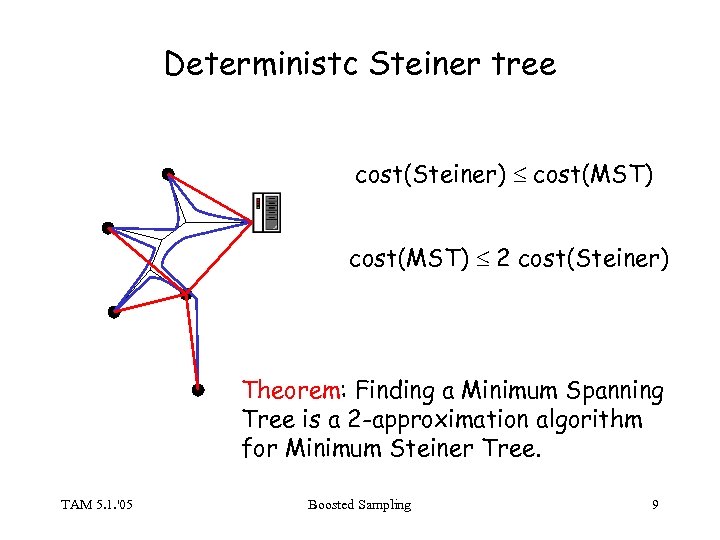
Deterministc Steiner tree cost(Steiner) cost(MST) 2 cost(Steiner) Theorem: Finding a Minimum Spanning Tree is a 2 -approximation algorithm for Minimum Steiner Tree. TAM 5. 1. '05 Boosted Sampling 9

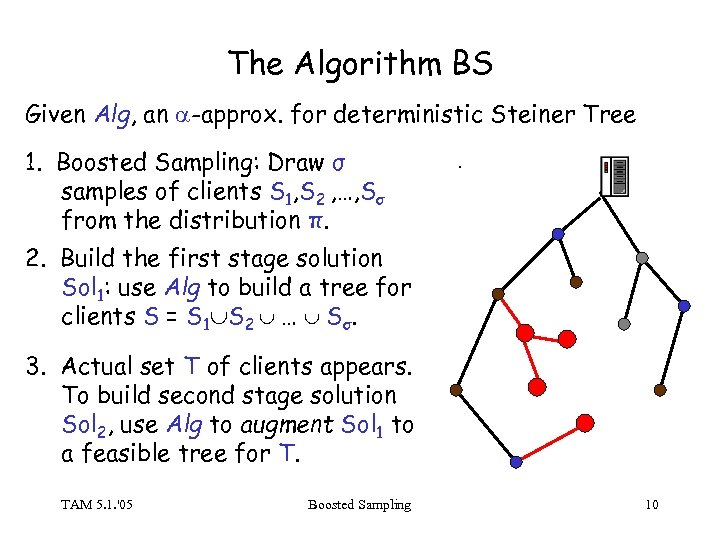
The Algorithm BS Given Alg, an -approx. for deterministic Steiner Tree 1. Boosted Sampling: Draw σ samples of clients S 1, S 2 , …, Sσ from the distribution π. . 2. Build the first stage solution Sol 1: use Alg to build a tree for clients S = S 1 S 2 … Sσ. 3. Actual set T of clients appears. To build second stage solution Sol 2, use Alg to augment Sol 1 to a feasible tree for T. TAM 5. 1. '05 Boosted Sampling 10

Is BS any good? Theorem: Boosted sampling algorithm is a 4 -approximation for Stochastic Steiner Tree (assuming Alg is a 2 -approx. . ). Nothing special about Steiner Tree; BS works for other problems: Facility Location, Steiner Network, Vertex Cover. . Idea: Bound stage costs separately • First stage cheap, because not too many samples, and Alg is good • Second stage is cheap, because samples “dense enough” TAM 5. 1. '05 Boosted Sampling 11

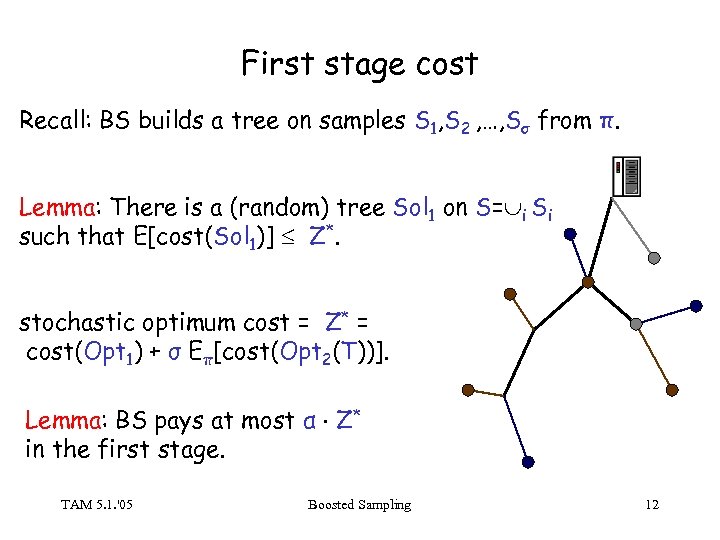
First stage cost Recall: BS builds a tree on samples S 1, S 2 , …, Sσ from π. Lemma: There is a (random) tree Sol 1 on S= i Si such that E[cost(Sol 1)] Z*. stochastic optimum cost = Z* = cost(Opt 1) + σ Eπ[cost(Opt 2(T))]. Lemma: BS pays at most α Z* in the first stage. TAM 5. 1. '05 Boosted Sampling 12

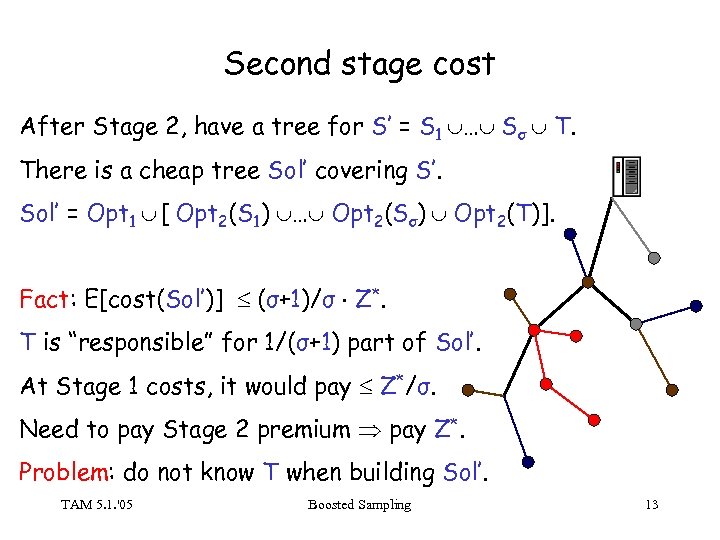
Second stage cost After Stage 2, have a tree for S’ = S 1 … Sσ T. There is a cheap tree Sol’ covering S’. Sol’ = Opt 1 [ Opt 2(S 1) … Opt 2(Sσ) Opt 2(T)]. Fact: E[cost(Sol’)] (σ+1)/σ Z*. T is “responsible” for 1/(σ+1) part of Sol’. At Stage 1 costs, it would pay Z*/σ. Need to pay Stage 2 premium pay Z*. Problem: do not know T when building Sol’. TAM 5. 1. '05 Boosted Sampling 13

Idea: cost sharing Scenario 1: Scenario 2: Pretend to build a solution for S’ = S T. Build a solution Alg(S) for S. Charge each j S’ some amount ξ(S’, j). Augment Alg(S) to a valid solution for S’ = S T. Assume: j S’ ξ(S’, j) Opt(S’) We argued: E[ j T ξ(S’, j)] Z*/σ (by symmetry) Want to prove: Augmenting cost in Scenario 2 β j T ξ(S’, j) TAM 5. 1. '05 Boosted Sampling 14

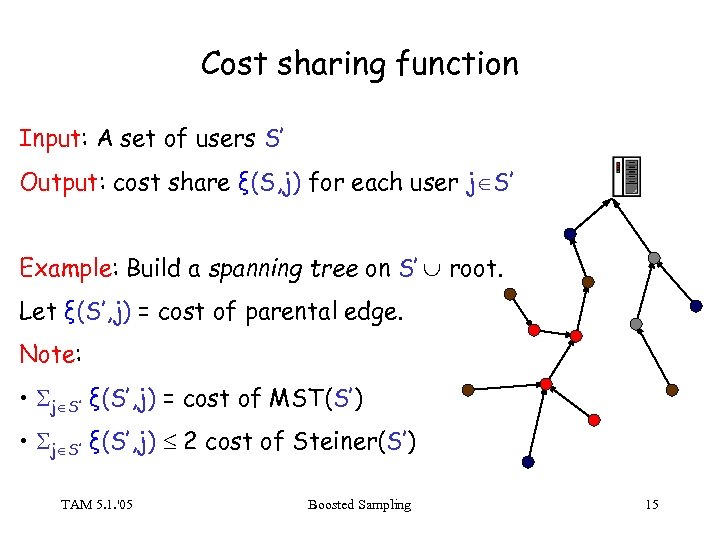
Cost sharing function Input: A set of users S’ Output: cost share ξ(S, j) for each user j S’ Example: Build a spanning tree on S’ root. Let ξ(S’, j) = cost of parental edge. Note: • j S’ ξ(S’, j) = cost of MST(S’) • j S’ ξ(S’, j) 2 cost of Steiner(S’) TAM 5. 1. '05 Boosted Sampling 15

Strictness A csf ξ( , ) is β-strict, if cost of Augment(Alg(S), T) β j T ξ(S T, j) for any S, T Users. Second stage cost = σ cost(Augment(Alg( i Si), T)) σ β j T ξ( j Sj T, j) S Fact: E[shares of T] Z*/σ Hence: E[second stage cost] σ β Z*/σ = β Z*. TAM 5. 1. '05 Boosted Sampling T 16

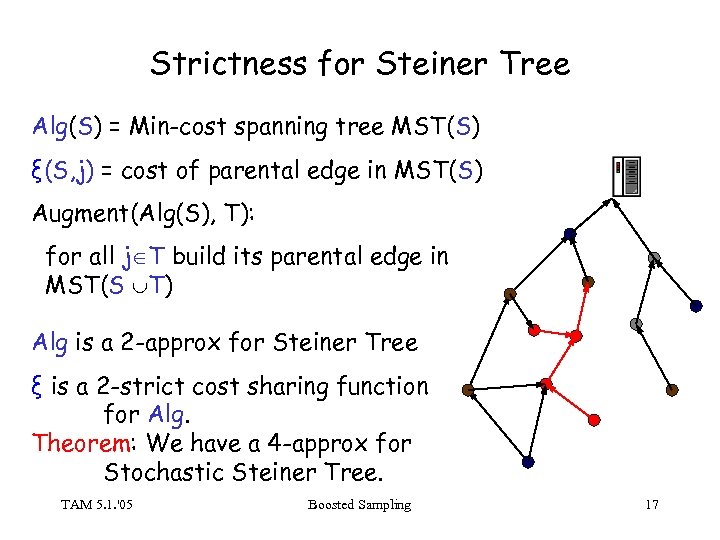
Strictness for Steiner Tree Alg(S) = Min-cost spanning tree MST(S) ξ(S, j) = cost of parental edge in MST(S) Augment(Alg(S), T): for all j T build its parental edge in MST(S T) Alg is a 2 -approx for Steiner Tree ξ is a 2 -strict cost sharing function for Alg. Theorem: We have a 4 -approx for Stochastic Steiner Tree. TAM 5. 1. '05 Boosted Sampling 17

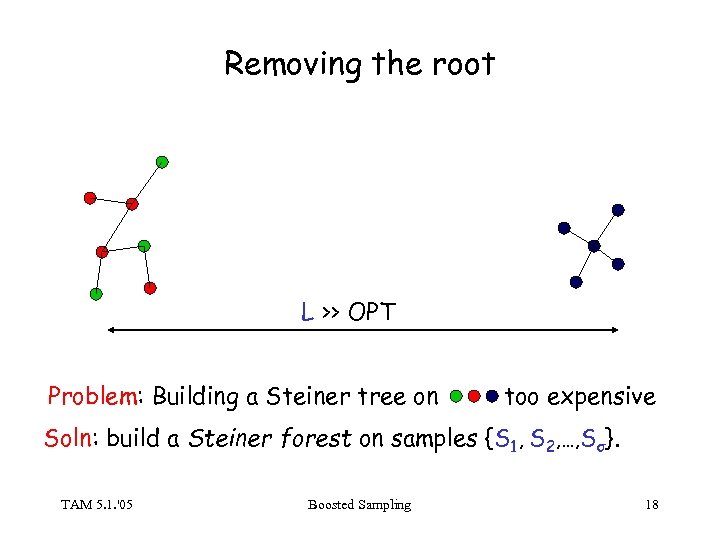
Removing the root L >> OPT Problem: Building a Steiner tree on too expensive Soln: build a Steiner forest on samples {S 1, S 2, …, Sσ}. TAM 5. 1. '05 Boosted Sampling 18

Works for other problems, too BS works for any problem that is - subadditive (union of solns for S, T is a soln for S T) - has α-approx algo that admits β-strict cost sharing Constant approximation algorithms for stochastic Facility Location, Vertex Cover, Steiner Network. . (hard part: prove strictness) TAM 5. 1. '05 Boosted Sampling 19

What if σ is random? Suppose σ is also a random variable. π(S, σ) – joint distribution For i=1, 2, …, σmax do sample (Si, σi) from π with prob. σi/σmax accept Si Let S be the union of accepted Si’s Output Alg(S) as the first stage solution TAM 5. 1. '05 Boosted Sampling 20

Multistage problems Three stage stochastic Steiner Tree: • On Monday, edges cost 1. We only know the probability distribution π. • On Tuesday, results of a market survey come in. We gain some information I, and update π to the conditional distribution π|I. Edges cost σ1. • On Wednesday, clients finally show up. Edges now cost σ2 (σ2>σ1), and we must buy enough to connect all clients. Theorem: There is a 6 -approximation for three stage stochastic Steiner Tree (in general, 2 k approximation for k stage problem) TAM 5. 1. '05 Boosted Sampling 21

Conclusions We have seen a randomized algorithm for a stochastic problem: using sampling to solve problems involving randomness. • Do we need strict cost sharing? Our proof requires strictness – maybe there is a weaker property? Maybe we can prove guarantees for arbitrary subadditive problems? • Prove full strictness for Steiner Forest – so far we have only uni-strictness. • Cut problems: Can we say anything about Multicut? Singlesource multicut? TAM 5. 1. '05 Boosted Sampling 22

+++THE++END+++ Note that if π consists of a small number of scenarios, this can be transformed to a deterministic problem. Find Sol 1 Elems and Sol 2 : 2 Users 2 Elems to minimize cost(Sol 1) + σ Eπ(T)[cost(Sol 2(T))] subject to satisfied(j, Sol 1 Sol 2(T)) for all sets T Users and all j T . TAM 5. 1. '05 Boosted Sampling 23

Related work • Stochastic linear programming dates back to works of Dantzig, Beale in the mid-50’s • Scheduling literature, various distributions of job lengths • Resource installation [Dye, Stougie&Tomasgard 03] • Single stage stochastic: maybecast [Karger&Minkoff 00], bursty connections [Kleinberg, Rabani&Tardos 00]… • Stochastic versions of NP-hard problems (restricted π) [Ravi&Sinha 03], [Immorlica, Karger, Minkoff&Mirrokni 04] • Stochastic LP solving&rounding: [Shmoys&Swamy 04] TAM 5. 1. '05 Boosted Sampling 24

Infrastructure Design Problems Assumption: Sol is a set of elements cost(Sol) = elem Sol cost(elem) Facility location: satisfied(j) iff j connected to an open facility Vertex Cover: satisfied(e={uv}) iff u or v in the cover Connectivity problems: satisfied(j) iff j’s terminals connected Cut problems: satisfied(j) iff j’s terminals disconnected TAM 5. 1. '05 Boosted Sampling 25

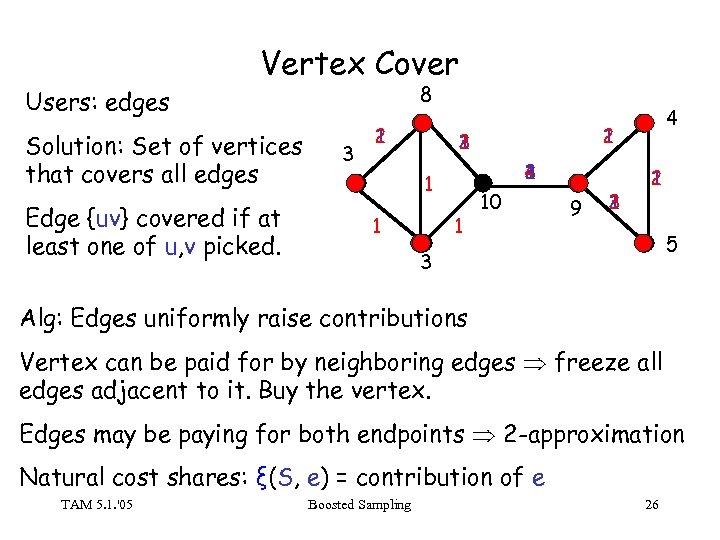
Vertex Cover 8 Users: edges Solution: Set of vertices that covers all edges Edge {uv} covered if at least one of u, v picked. 3 2 1 3 4 2 1 1 4 10 9 3 2 1 5 3 Alg: Edges uniformly raise contributions Vertex can be paid for by neighboring edges freeze all edges adjacent to it. Buy the vertex. Edges may be paying for both endpoints 2 -approximation Natural cost shares: ξ(S, e) = contribution of e TAM 5. 1. '05 Boosted Sampling 26

Strictness for Vertex Cover 1 S = blue edges T = red edge 1 1 1 n+1 1 1 n Alg(S) = blue vertices: Augment(Alg(S), T) costs (n+1) gap Ω(n)! ξ(S T, T) =1 • Find a better ξ? Do not know how. Instead, make Alg(S) buy a center vertex. TAM 5. 1. '05 Boosted Sampling 27

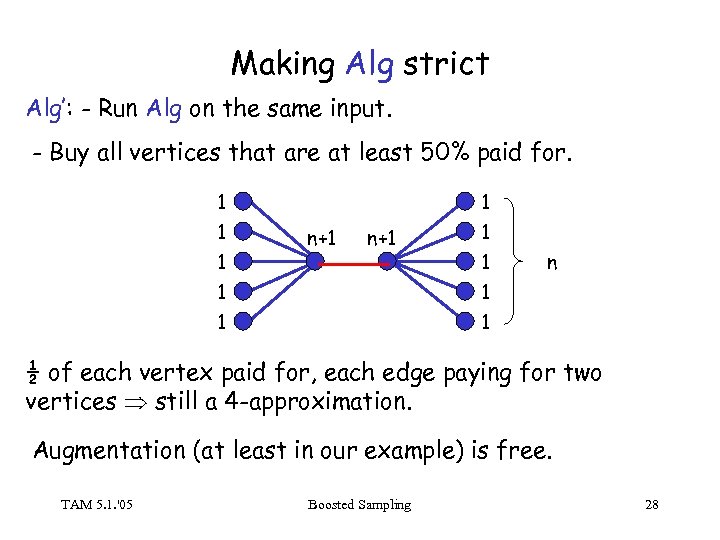
Making Alg strict Alg’: - Run Alg on the same input. - Buy all vertices that are at least 50% paid for. 1 1 1 n+1 1 1 n 1 1 ½ of each vertex paid for, each edge paying for two vertices still a 4 -approximation. Augmentation (at least in our example) is free. TAM 5. 1. '05 Boosted Sampling 28

Why should strictness hold? Alg’: - Run Alg on the same input. - Buy all vertices that are at least 50% paid for. Alg(S T) α 1 α 2 α 3 v α 1 ’ α 2’ S = blue edges T = red edges Suppose vertex v fully paid for in Alg(S T). • If j T αj’ ≥ ½ cost(v) , then T can pay for ¼ of v in the augmentation step. • If j S αj ≥ ½ cost(v), then v would be open in Alg(S). (almost. . need to worry that Alg(S T) and Alg(S) behave differently. ) TAM 5. 1. '05 Boosted Sampling 29

Metric facility location Input: a set of facilities and a set of cities living in a metric space. Solution: Set of open facilities, a path from each city to an open facility. “Off the shelf” components: 3 -approx. algorithm [Mettu&Plaxton 00]. Turns out that cost sharing fn [P. &Tardos 03] is 5. 45 strict. Theorem: There is a 8. 45 -approx for stochastic FL. TAM 5. 1. '05 Boosted Sampling 30

Steiner Network client j = pair of terminals sj, tj satisfied(j): sj, tj connected by a path 2 -approximation algorithms known ([Agarwal, Klein&Ravi 91], [Goemans&Williamson 95]), but do not admit strict cost sharing. [Gupta, Kumar, P. , Roughgarden 03]: 4 -approx algorithm that admits 4 -uni-strict cost sharing Theorem: 8 -approx for Stochastic Steiner Network in the “independent coinflips” model. TAM 5. 1. '05 Boosted Sampling 31

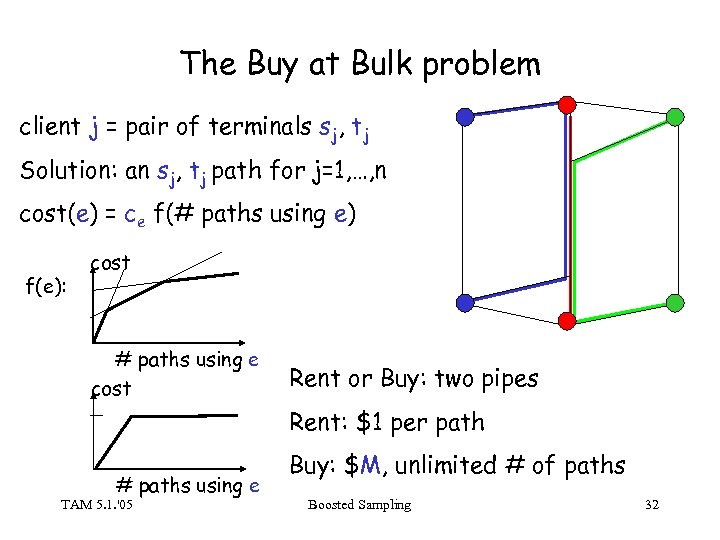
The Buy at Bulk problem client j = pair of terminals sj, tj Solution: an sj, tj path for j=1, …, n cost(e) = ce f(# paths using e) f(e): cost # paths using e cost Rent or Buy: two pipes Rent: $1 per path # paths using e TAM 5. 1. '05 Buy: $M, unlimited # of paths Boosted Sampling 32

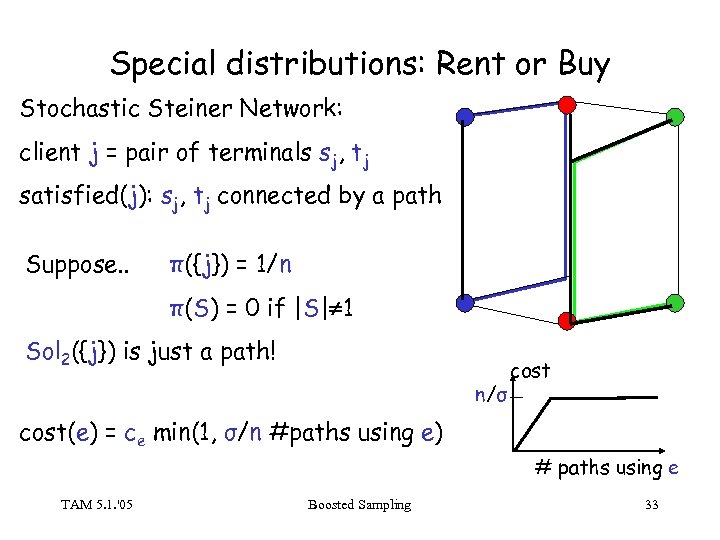
Special distributions: Rent or Buy Stochastic Steiner Network: client j = pair of terminals sj, tj satisfied(j): sj, tj connected by a path Suppose. . π({j}) = 1/n π(S) = 0 if |S| 1 Sol 2({j}) is just a path! n/σ cost(e) = ce min(1, σ/n #paths using e) # paths using e TAM 5. 1. '05 Boosted Sampling 33

Rent or Buy The trick works for any problem P. (can solve Rent-or-Buy Vertex Cover, . . ) These techniques give the best approximation for Single. Sink Rent-or-Buy (3. 55 approx [Gupta, Kumar, Roughgarden 03]), and Multicommodity Rent or Buy (8 -approx [Gupta, Kumar, P. , Roughgarden 03], 6. 83 -approx [Becchetti, Konemann, Leonardi, P. 04]). “Bootstrap” to stochastic Rent-or-Buy: - 6 approximation for Stochastic Single-Sink Ro. B - 12 approx for Stochastic Multicommodity Ro. B (indep. coinflips) TAM 5. 1. '05 Boosted Sampling 34

Performance Guarantee Theorem: Let P be a sub-additive problem, with α-approximation algorithm, that admits β-strict cost sharing. Stochastic(P) has (α+β) approx. Corollary: Stochastic Steiner Tree, Facility Location, Vertex Cover, Steiner Network (restricted model)… have constant factor approximation algorithms. Corollary: Deterministic and stochastic Rent-or-Buy versions of these problems have constant approximations. TAM 5. 1. '05 Boosted Sampling 35