Boolean Logic ITI 1121 N El Kadri

Зарегистрируйтесь, чтобы просмотреть полный документ!

Boolean Logic ITI 1121 N. El Kadri

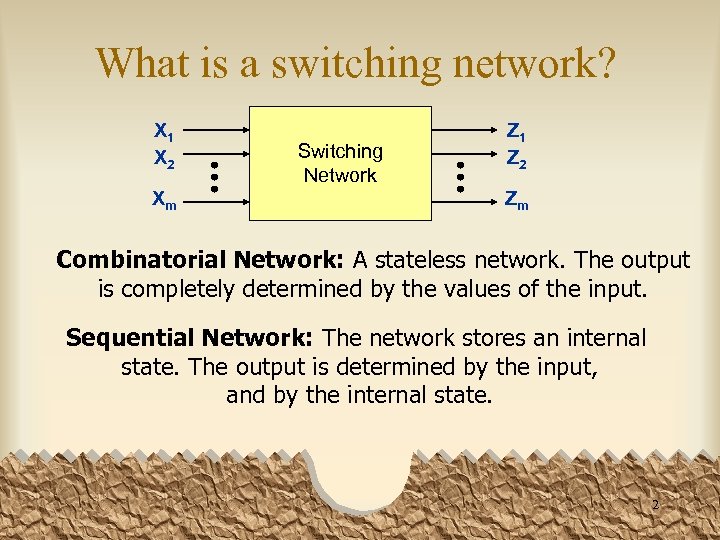
What is a switching network? X 1 X 2 Xm Switching Network Z 1 Z 2 Zm Combinatorial Network: A stateless network. The output is completely determined by the values of the input. Sequential Network: The network stores an internal state. The output is determined by the input, and by the internal state. 2

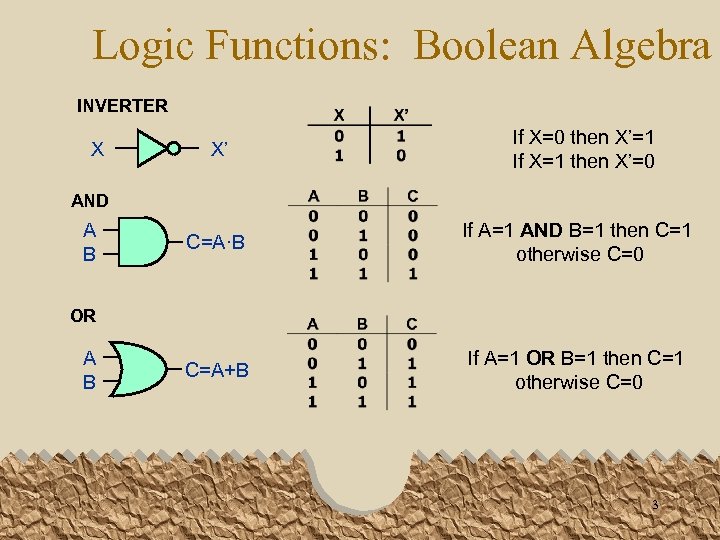
Logic Functions: Boolean Algebra INVERTER X X’ If X=0 then X’=1 If X=1 then X’=0 AND A B C=A·B If A=1 AND B=1 then C=1 otherwise C=0 C=A+B If A=1 OR B=1 then C=1 otherwise C=0 OR A B 3

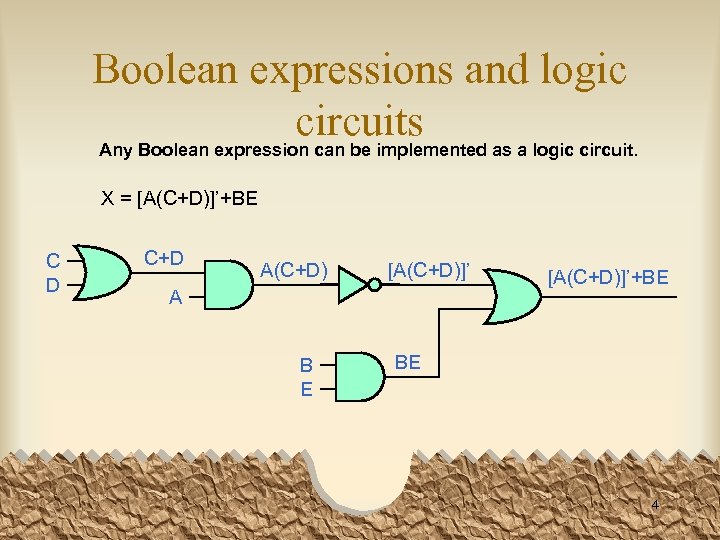
Boolean expressions and logic circuits Any Boolean expression can be implemented as a logic circuit. X = [A(C+D)]’+BE C D C+D A(C+D) [A(C+D)]’ A B E [A(C+D)]’+BE BE 4

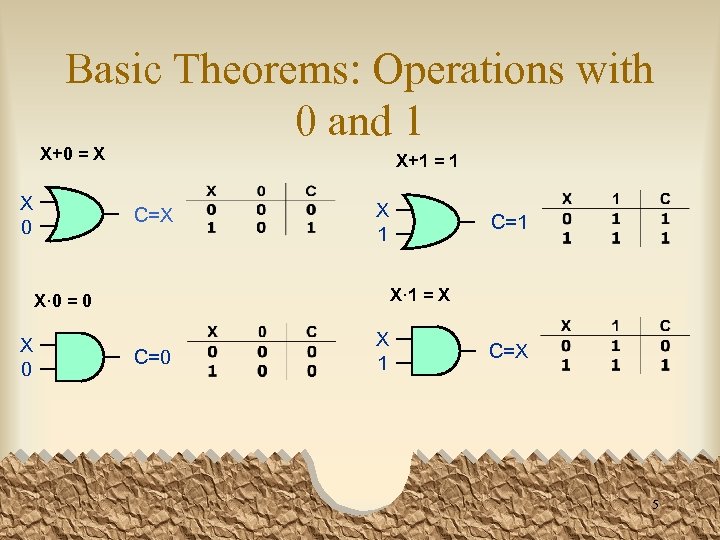
Basic Theorems: Operations with 0 and 1 X+0 = X X 0 X+1 = 1 C=X X 1 X· 1 = X X· 0 = 0 X 0 C=1 C=0 X 1 C=X 5

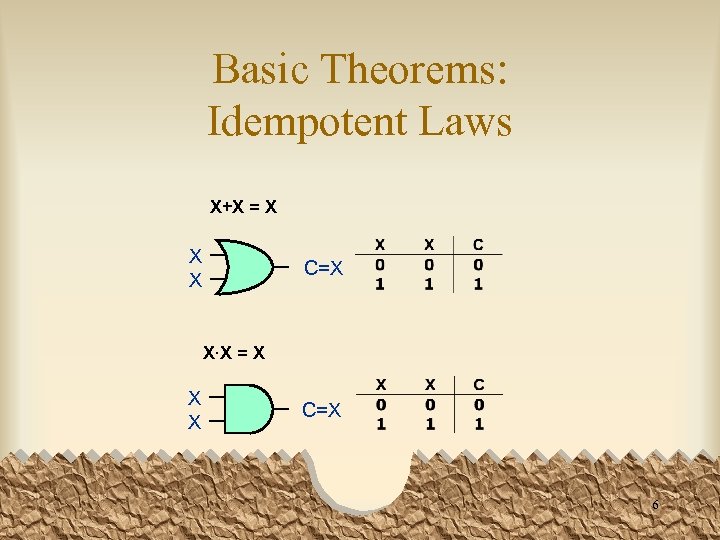
Basic Theorems: Idempotent Laws X+X = X X X C=X X·X = X X X C=X 6

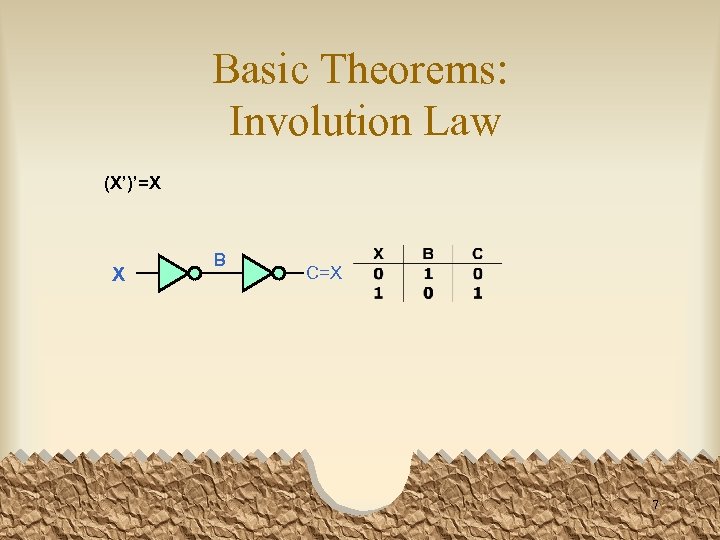
Basic Theorems: Involution Law (X’)’=X X B C=X 7

Basic Theorems: Laws of Complementarity X+X’ = 1 X X’ C=1 X·X’ = 0 X X’ C=0 8

Expression Simplification using the Basic Theorems X can be an arbitrarily complex expression. Simplify the following boolean expressions as much as you can using the basic theorems. (AB’ + D)E + 1 = 1 (AB’ + D)’ = 0 (AB + CD) + (CD + A) + (AB + CD)’ = 1 9

Associative Law (X+Y)+Z = X+(Y+Z) X Y Z C Y Z X C 10

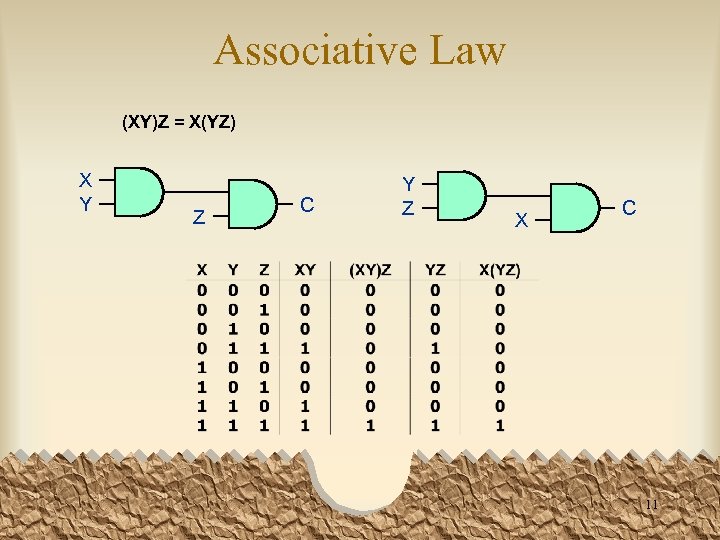
Associative Law (XY)Z = X(YZ) X Y Z C Y Z X C 11

First Distributive Law X(Y+Z) = XY+XZ 12

First Distributive Law X(Y+Z) = XY+XZ 13

First Distributive Law X(Y+Z) = XY+XZ 14

First Distributive Law X(Y+Z) = XY+XZ 15

First Distributive Law X(Y+Z) = XY+XZ 16

Second Distributive Law X+YZ = (X+Y)(X+Z) 17

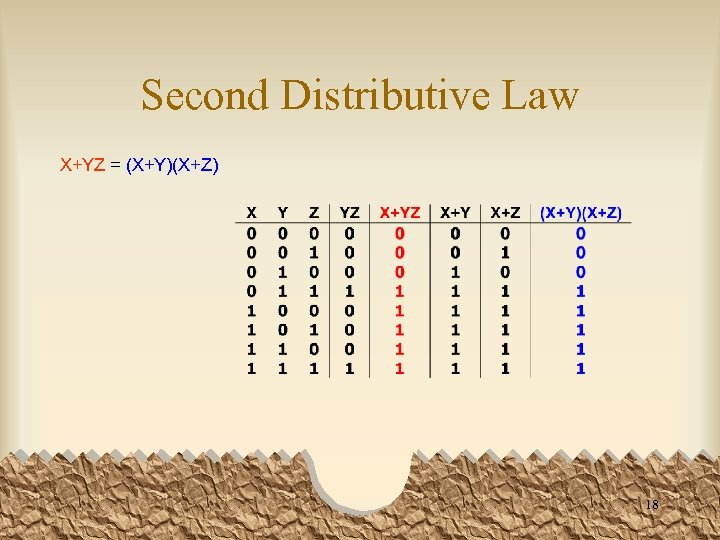
Second Distributive Law X+YZ = (X+Y)(X+Z) 18

Second Distributive Law (A different proof) (X + Y)(X + Z) = X(X + Z) + Y(X + Z) (using the first distributive law) = XX + XZ + YX + YZ (using the first distributive law) = X + XZ + YX + YZ (using the idempotent law) = X· 1 + XZ + YX + YZ (using the operation with 1 law) = X(1 + Z + Y) + YZ (using the first distributive law) = X· 1 + YZ (using the operation with 1 law) = X + YZ (using the operation with 1 law) 19

Simplification Theorems XY + XY’ = X(Y + Y’) = X· 1 = X X + XY = X X(1 + Y) = X· 1 = X (X + Y’)Y = XY XY + Y’Y = XY + 0 = XY (X + Y)(X + Y’) = XX + XY’ + YX + YY’ = X + X(Y’ + Y) + 0 = X + X· 1 =X X(X + Y) = XX + XY = X· 1 + XY = X(1 + Y) = X· 1 = X XY’ + Y = X + Y (using the second distributive law) XY’ + Y = Y + XY’ = (Y + X)(Y + Y’) = (Y + X)· 1 = X + Y 20

Examples Simplify the following expressions: W = [M + N’P + (R + ST)’][M + N’P + R + ST] X = M + N’P Y = R + ST W = (X + Y’)(X + Y) W = XX + XY + Y’X + Y’Y W = X· 1 + XY’ + 0 W = X + X(Y + Y’) = X + X· 1 = X W = M + N’P 21

Скачать презентацию Boolean Logic ITI 1121 N El Kadri

365f3ba912c794099e8c4b13e5627654.ppt

Количество слайдов: 21