БОНУС ар — среднее арифметическое кв

Зарегистрируйтесь, чтобы просмотреть полный документ!

БОНУС ар = - среднее арифметическое; кв = - среднее квадратическое; геом = лог = вз = - среднее геометрическое; , где = - сред. логарифмическое ; , где k – коэффициент взвешивания – среднее взвешанное

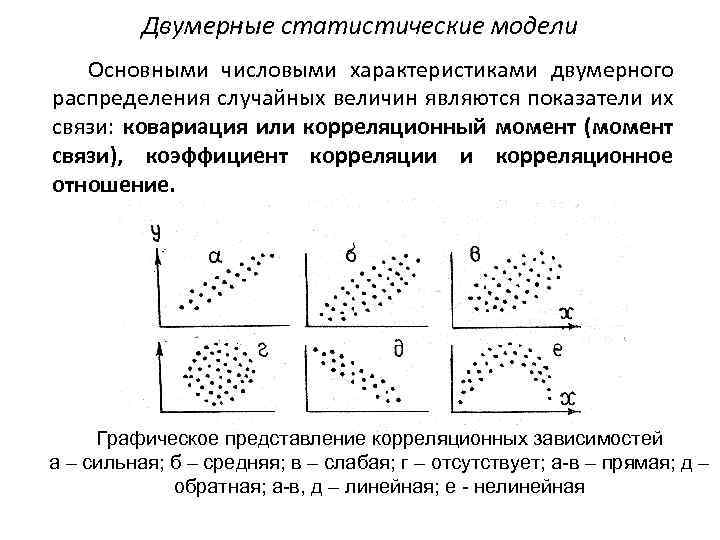
Двумерные статистические модели Основными числовыми характеристиками двумерного распределения случайных величин являются показатели их связи: ковариация или корреляционный момент (момент связи), коэффициент корреляции и корреляционное отношение. Графическое представление корреляционных зависимостей а – сильная; б – средняя; в – слабая; г – отсутствует; а-в – прямая; д – обратная; а-в, д – линейная; е - нелинейная

Для оценки степени зависимости двух случайных величин X и Y используется корреляционный момент Kxy. Для дискретных случайных величин корреляционный момент определяется формулой: -здесь n - число наблюдений случайных величин X и Y; X, Y - средние значения случайных величин X и Y соответственно. Для независимых случайных величин корреляционный момент равен нулю, в противном случае существует зависимость между случайными величинами.

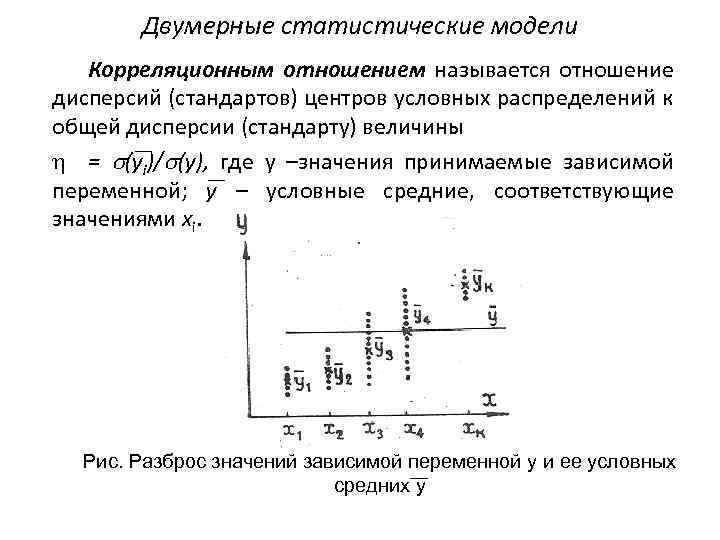
Двумерные статистические модели Корреляционным отношением называется отношение дисперсий (стандартов) центров условных распределений к общей дисперсии (стандарту) величины = (yi)/ (y), где y –значения принимаемые зависимой переменной; y – условные средние, соответствующие значениями xi. Рис. Разброс значений зависимой переменной y и ее условных средних y

Равенство = 0 – необходимое и достаточное условие отсутствия корреляционной зависимости. При = 1 корреляционная связь переходит в функциональную, когда все значения переменной, соответствующие определенному xi соответствует одно единственное yi.

Для характеристики связи между величинами (X, Y) в чистом виде переходят от момента Кxу к безразмерной характеристике (выборочный коэффициент корреляции Пирсона) где - x, y среднеквадратические отклонения величин X, Y. Эта характеристика называется коэффициентом парной корреляции величин Х и Y. Если коэффициент корреляции двух случайных величин равен нулю, то такие случайные величины называются некоррелируемыми (независимыми). При значениях коэффициента корреляции близких к единице – коррелируемыми. В случае, когда значение коэффициента корреляции, между двумя случайными величинами, близко к минус единице, считается, что между случайными величинами существует сильная обратная корреляционная связь.

Таким образом, характеризует степень тесноты линейной зависимости между Y и X , проявляющейся в том, что при возрастании одной случайной величины другая проявляет тенденцию также возрастать (в этом случае > 0 ) или убывать (в таком случае < 0 ). В первом случае говорят, что Y и X связаны положительной корреляцией, а во втором корреляция отрицательна.

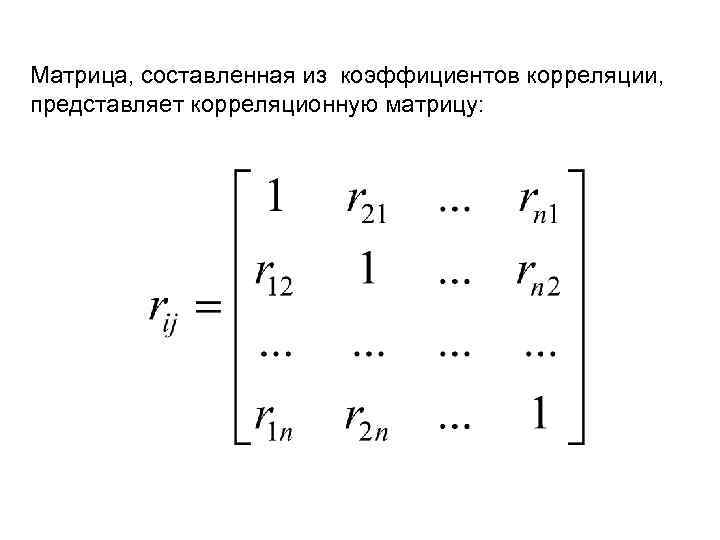
Матрица, составленная из коэффициентов корреляции, представляет корреляционную матрицу:

Если не удается проверить гипотезу о соответствии эмпирического распределения определенному закону из-за малого количества данных (или распределения существенно отличаются от нормального закона), то для проверки гипотезы о наличии корреляционной связи можно использовать ранговый коэффициент корреляции Спирмена. Его расчет основан на замене выборочных значений исследуемых случайных величин их рангами в порядке возрастания. При этом предполагается, что если между значениями случайных величин нет корреляционной зависимости, то ранги этих величин тоже будут независимыми. r=1– , где di разность рангов сопряженных значений изучаемых величин xi и yi; n – количество пар в выборке

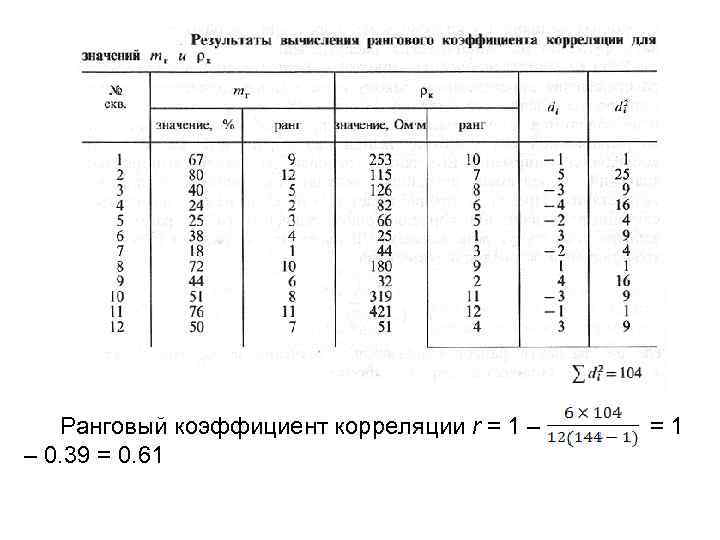
Ранговый коэффициент корреляции r = 1 – – 0. 39 = 0. 61 =1

Множественная корреляция Корреляция двух случайных величин X и Y – частный случай более распространенной в окружающей нас действительности множественной корреляции, когда изменение одной из переменных зависти от изменения множества других. При исследовании таких связей возникает две существенно отличных друг от друга задачи: - определение тесноты связи между парами факторов, когда влияние других исключено; - Тесноты линейной зависимости между одним из факторов (функцией) и остальными (аргументами). Показатель, характеризующий тесноту линейной связи между двумя признаками X и Y, когда влияние других факторов исключено, называется частным коэффициентом корреляции.

Множественная корреляция Для трех признаков – X, Y, Z вычисляются следующие частные коэффициенты корреляции: - взаимодействие между X и Y при фиксированном Z rxy. z = - взаимодействие между X и Z при фиксированном Y rxz. y = - взаимодействие между X и Z при фиксированном Y ryz. x =

Множественная корреляция Показателем тесноты связи между одним из факторов и остальными является коэффициент множественной корреляции. Для зависимости X от Y и Z и его вычисляют по формуле Rx =

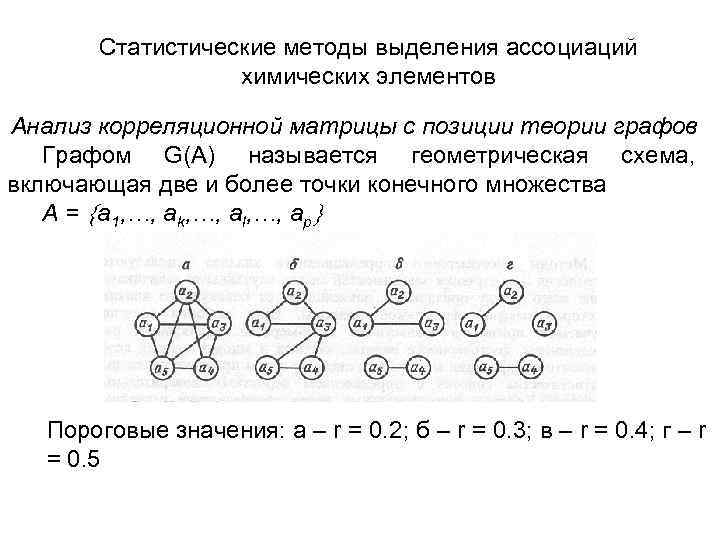
Статистические методы выделения ассоциаций химических элементов Анализ корреляционной матрицы с позиции теории графов Графом G(A) называется геометрическая схема, включающая две и более точки конечного множества А = а 1, …, аk, …, al, …, ap Пороговые значения: а – r = 0. 2; б – r = 0. 3; в – r = 0. 4; г – r = 0. 5

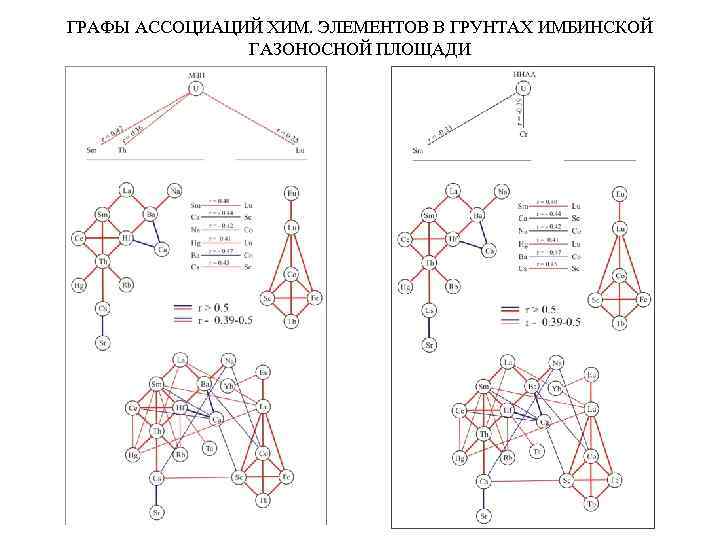
ГРАФЫ АССОЦИАЦИЙ ХИМ. ЭЛЕМЕНТОВ В ГРУНТАХ ИМБИНСКОЙ ГАЗОНОСНОЙ ПЛОЩАДИ

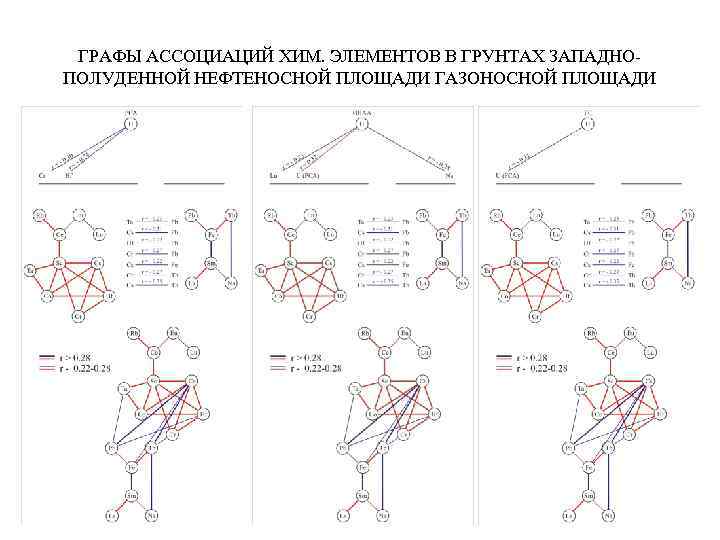
ГРАФЫ АССОЦИАЦИЙ ХИМ. ЭЛЕМЕНТОВ В ГРУНТАХ ЗАПАДНОПОЛУДЕННОЙ НЕФТЕНОСНОЙ ПЛОЩАДИ ГАЗОНОСНОЙ ПЛОЩАДИ

Кластерный анализ (дендрограммы) Результаты кластер-анализа изображаются в виде деревовидного графа – дендрограммы, в которой по оси абсцисс располагаются символические обозначения объектов исследования (векторов матрицы), а по оси ординат – минимальные значения дистанционных коэффициентов, соответствующих каждому шагу классифицированной процедуры. Первый шаг состоит в выявлении нивысших коэффициентов корреляций между отдельными парами, которые объединяются и принимаются за центры групп. Число таких центров может изменяться от одного до трех (редко более).

Кластерный анализ (дендрограммы) Второй шаг – матрица вычисляется снова, причем сгруппированные элементы считаются за один элемент, а коэффициенты их корреляции с другими группами вычисляются заново с помощью различных методов осреднения. По результатам вычисления составляется новая матрица, меньшей размерности, в которой изменяются лишь значения коэффициентов, связанные с членами объединенных групп. Сокращенная и пересчитанная матрица вновь подвергается сокращению, путем выявления и объединения пар с максимальными признаками сходства, и последующим осреднением новых групповых коэффициентов.

Кластерный анализ (дендрограммы) Операция последовательного сокращения и пересчета коэффициентов матрицы повторяется до тех пор, пока значения групповых коэффициентов сходства не достигнут порогового значения или размерность матрицы не станет минимальной. В качестве меры сходства используются непосредственно парные коэффициенты корреляции (1 - r), m-мерное эвклидово расстояние или другие дистанционные коэффициенты.

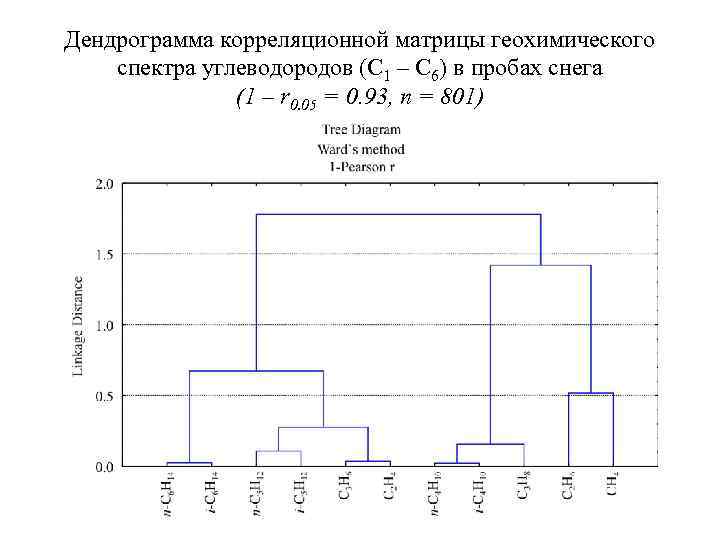
Дендрограмма корреляционной матрицы геохимического спектра углеводородов (С 1 – С 6) в пробах снега (1 – r 0. 05 = 0. 93, n = 801)

Метод главных компонент С увеличением размерности признакового пространства возрастают трудности изучения природных объектов и возникает проблема замены многочисленных наблюдаемых признаков меньшим их числом, без существенной потери полезной информации. Одним из наиболее распространенных методов решения этой задачи является метод главных компонент. Основой метода является линейное преобразование m исходных переменных (признаков) в m новых переменных, где каждая новая переменная представляет собой линейное сочетание исходных. В процессе преобразования векторы наблюдаемых переменных заменяются новыми векторами (главными компонентами), которые вносят резко различные вклады в суммарную дисперсию многомерных признаков.

Метод главных компонент Сокращение пространства признаков достигается путем отбора нескольких наиболее информативных компонент, обеспечивающих основную долю суммарной дисперсии, что приводит к заметному уменьшению их общего числа за счет наименее информативных компонент, отражающих малые доли суммарной дисперсии Главные компоненты – это собственные векторы ковариационных матриц исходных признаков. Координаты собственных векторов рассматриваются как нагрузки соответствующих переменных на тот или иной фактор. Как правило, дисперсия одной из главных компонент достигает половины и более от суммарной дисперсии а в совокупности с дисперсиями еще одной-двух последующих компонент, их общий вклад в суммарную дисперсию превышает 90%.

Метод главных компонент Таким образом, без существенной потери информации об изменчивости наблюденных признаков можно заметно сократить размерность пространства наблюденных признаков (до p m), ограничившись данными по двум-трем наиболее главным компонентам. Метод главных компонент используется в качестве основы факторного анализа многомерных совокупностей. В практике используют два метода факторного анализа Rи Q-метод. R-метод основан на использовании не ковариационной, а корреляционной матрицы. Для более содержательной интерпретации результаты факторного анализа подвергаются процедуре «вращения» вокруг центра координат, для выявления наиболее контрастных сочетаний факторных нагрузок.

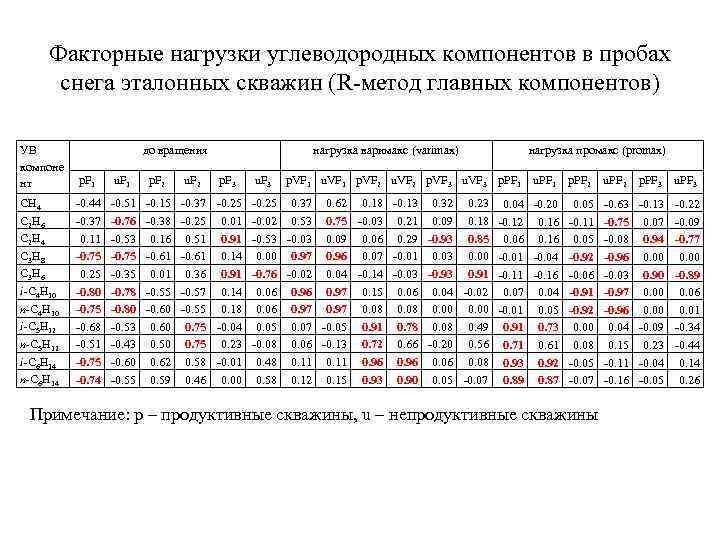
Факторные нагрузки углеводородных компонентов в пробах снега эталонных скважин (R-метод главных компонентов) УВ компоне нт до вращения нагрузка варимакс (varimax) p. F 1 u. F 1 p. F 2 u. F 2 CH 4 С 2 H 6 С 2 H 4 C 3 H 8 C 3 H 6 i-C 4 H 10 n-C 4 H 10 i-C 5 H 12 n-C 5 H 12 i-C 6 H 14 n-C 6 H 14 -0. 44 -0. 37 0. 11 -0. 75 0. 25 -0. 80 -0. 75 -0. 68 -0. 51 -0. 75 -0. 74 -0. 51 -0. 76 -0. 53 -0. 75 -0. 35 -0. 78 -0. 80 -0. 53 -0. 43 -0. 60 -0. 55 -0. 15 -0. 38 0. 16 -0. 61 0. 01 -0. 55 -0. 60 0. 50 0. 62 0. 59 -0. 37 -0. 25 0. 37 0. 62 0. 18 -0. 13 0. 32 0. 23 0. 04 -0. 20 0. 05 -0. 63 -0. 13 -0. 22 -0. 25 0. 01 -0. 02 0. 53 0. 75 -0. 03 0. 21 0. 09 0. 18 -0. 12 0. 16 -0. 11 -0. 75 0. 07 -0. 09 0. 51 0. 91 -0. 53 -0. 03 0. 09 0. 06 0. 29 -0. 93 0. 85 0. 06 0. 16 0. 05 -0. 08 0. 94 -0. 77 -0. 61 0. 14 0. 00 0. 97 0. 96 0. 07 -0. 01 0. 03 0. 00 -0. 01 -0. 04 -0. 92 -0. 96 0. 00 0. 36 0. 91 -0. 76 -0. 02 0. 04 -0. 14 -0. 03 -0. 93 0. 91 -0. 16 -0. 03 0. 90 -0. 89 -0. 57 0. 14 0. 06 0. 97 0. 15 0. 06 0. 04 -0. 02 0. 07 0. 04 -0. 91 -0. 97 0. 00 0. 06 -0. 55 0. 18 0. 06 0. 97 0. 08 0. 00 -0. 01 0. 05 -0. 92 -0. 96 0. 00 0. 01 0. 75 -0. 04 0. 05 0. 07 -0. 05 0. 91 0. 78 0. 08 0. 49 0. 91 0. 73 0. 00 0. 04 -0. 09 -0. 34 0. 75 0. 23 -0. 08 0. 06 -0. 13 0. 72 0. 66 -0. 20 0. 56 0. 71 0. 61 0. 08 0. 15 0. 23 -0. 44 0. 58 -0. 01 0. 48 0. 11 0. 96 0. 06 0. 08 0. 93 0. 92 -0. 05 -0. 11 -0. 04 0. 14 0. 46 0. 00 0. 58 0. 12 0. 15 0. 93 0. 90 0. 05 -0. 07 0. 89 0. 87 -0. 07 -0. 16 -0. 05 0. 26 p. F 3 u. F 3 нагрузка промакс (promax) p. VF 1 u. VF 1 p. VF 2 u. VF 2 p. VF 3 u. VF 3 p. PF 1 u. PF 1 p. PF 2 Примечание: p – продуктивные скважины, u – непродуктивные скважины u. PF 2 p. PF 3 u. PF 3

Скачать презентацию БОНУС ар — среднее арифметическое кв

КТиСМ в ЭиПП (Соболев) - Лекция_11.ppt

Количество слайдов: 24