0916f832ddb1f41c1dbebec25ebc4033.ppt
- Количество слайдов: 14

Bold Stroke Advanced Algorithms CS 539/441 OR In Search Of Efficient General Solutions Joe Hoffert Joseph. W. Hoffert@Boeing. com January 13, 2003

Bold Stroke Outline • General Techniques For Polynomial Time Solutions – Greedy Algorithms – Dynamic Programming – Linear Programming • • Problems w/ unlikely Poly-time Solutions (NP Complete) Next best solutions (e. g. , Approximation Algorithms) Lower Bound Techniques On-Line/Dynamic Algorithms January 13, 2003

Bold Stroke Greedy Algorithms • Locally optimal choice leads to globally optimal solution. Will not often yield optimal solution. • Framework – Prove Greedy Choice Property Holds: • first step “g” made by greedy algorithm is part of some optimal solution (i. e. , using “g” does no worse than an arbitrary optimal solution) – Prove Optimal Substructure Property Holds • We need subproblem P’ of P left after g is chosen • P’ is optimally solved in S. That is, the solution to P’ contained within S is optimal for P’. • Examples: Earliest Deadline First (EDF) scheduling, Huffman coding January 13, 2003
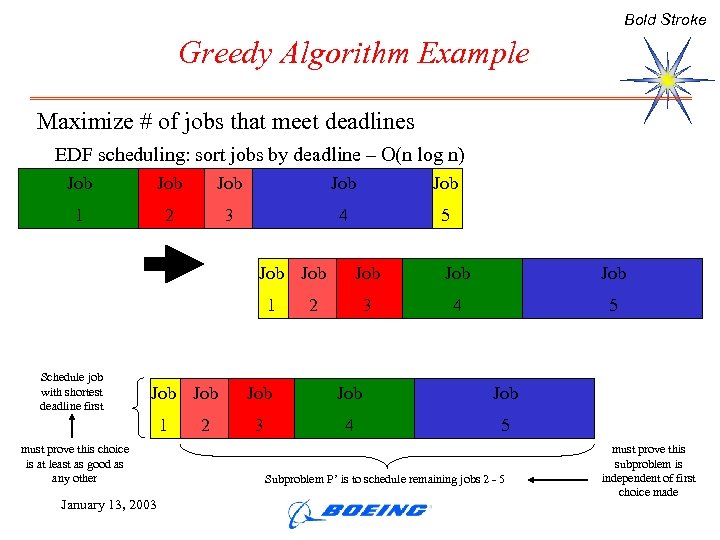
Bold Stroke Greedy Algorithm Example Maximize # of jobs that meet deadlines EDF scheduling: sort jobs by deadline – O(n log n) Job Job Job 1 2 3 4 5 Job 1 Schedule job with shortest deadline first Job 1 must prove this choice is at least as good as any other January 13, 2003 2 Job Job Job 3 4 5 Subproblem P’ is to schedule remaining jobs 2 - 5 must prove this subproblem is independent of first choice made

Bold Stroke Dynamic Programming • Locally optimal choice doesn’t lead to a globally optimal solution but there is still optimal substructure • Framework – Try all possible first choices: • One of these must be the correct first choice – Prove Optimal Substructure Property Holds • We need subproblem P’ of P left after first choice • P’ is optimally solved in S. That is, the solution S’ to P’ contained within S is optimal for P’. – Use bottom up approach to efficiently compute optimal cost for all subproblems (a. k. a. overlapping subproblems) • Examples: assembly line scheduling, longest common subsequence January 13, 2003
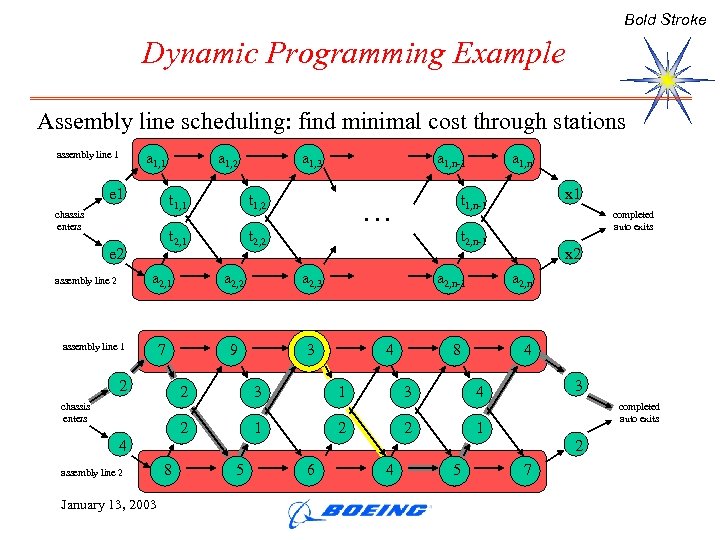
Bold Stroke Dynamic Programming Example Assembly line scheduling: find minimal cost through stations assembly line 1 a 1, 1 e 1 a 1, 2 a 1, 3 t 1, 1 e 2 t 1, 2 t 2, 1 chassis enters t 2, 2 a 2, 2 7 9 3 2 2 chassis enters 3 2 completed auto exits x 2 a 2, n-1 a 2, n 8 4 1 1 x 1 t 2, n-1 a 2, 3 assembly line 1 a 1, n t 1, n-1 … a 2, 1 assembly line 2 a 1, n-1 4 3 2 3 4 2 completed auto exits 1 4 assembly line 2 January 13, 2003 2 8 5 6 4 5 7
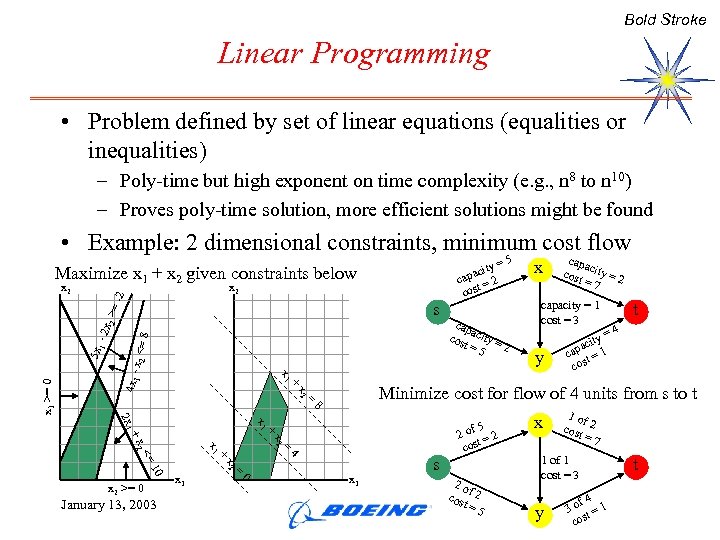
Bold Stroke Linear Programming • Problem defined by set of linear equations (equalities or inequalities) – Poly-time but high exponent on time complexity (e. g. , n 8 to n 10) – Proves poly-time solution, more efficient solutions might be found • Example: 2 dimensional constraints, minimum cost flow Maximize x 1 + x 2 given constraints below x 2 -2 x 2 4 x 1 x 2 <= 8 x 1 >= 0 5 x 1 - 2 x 2 >= s x 1 2 x 1 1 + x 2 x 1 <= 10 January 13, 2003 x 2 x x 2 >= 0 + + x 2 x 1 + = 0 = = ity = pac 2 ca = cost 5 cap a cos city = t= 2 5 x capa cost city = 2 =7 capacity = 1 cost = 3 y ty = aci 1 cap t = cos t 4 Minimize cost for flow of 4 units from s to t 8 4 x 1 s 5 2 of = 2 cost 2 o f cos 2 t= 5 x 1 of cost 2 =7 1 of 1 cost = 3 y f 4 3 o t=1 cos t

Bold Stroke NP-Complete Problems • NP complete problems are: – Complexity class Non-deterministic Polynomial (NP), i. e. , solution to NP problem can be verified in polynomial time – NP-hard, i. e. , reducible from all other NP problems in poly-time • Unlikely to have poly-time solutions, not (yet) proven • Example: MP-Scheduling problem Job 1 Job 2 Job 3 … Job n-1 n Is there a schedule in which all jobs are processed by specified time? January 13, 2003 Processor 1 2 Job 3 2 Processor 1 2 … … Processor m Job Job n n-1 1 Processor m-1 m

Bold Stroke Next Best Solutions • What to do when problem shown to be NP-complete: – Is problem a special case? For instance, vertex-cover is NPcomplete but if graph is a tree there exists a poly time algorithm for this case – Input size may be small enough not to be a problem – Use a heuristic and hope it gets something good enough – Use approximation algorithms (can be proven to be “good enough” or not “good enough”) • LP relaxation (IP is NP-complete, LP may give a good enough answer) • 0 -1 Knapsack relaxation to fractional knapsack • Non-preempted schedule relaxed to have preemption January 13, 2003

Bold Stroke Approximation Algorithms • Poly-time algorithms with provable bounds relative to optimal solution – If approximation bound is some constant n the algorithm is said to be an n-approximation • Example: 2 -approximation 0 -1 Knapsack problem Item 1 Item 2 Item 3 Item 4 Sort items by value per unit quantity (i. e. , total value/amount) and start filling up the knapsack Item 3 Item 1 Item 5 Item 2 January 13, 2003 Item 4 Item 5 Take the larger of the first item that won’t completely fit and the sum of all the previous items in the knapsack. This must be at least ½ of optimal solution which is a 2 approximation.

Bold Stroke Lower Bound Techniques • Determine minimum number of operations needed for any solution – Use decision-tree lower bound algorithm when applicable • All possibilities are enumerated as leaves in a decision tree • Traverse the depth of the tree • Example: lower bound for median among two sorted arrays – Adversary strategy • Devise a strategy that makes it “hard” for any algorithm to find a solution (i. e. , maximize the number of steps needed for any solution) • Example: merging two sorted arrays • Provides guidance for how good an algorithm can be January 13, 2003
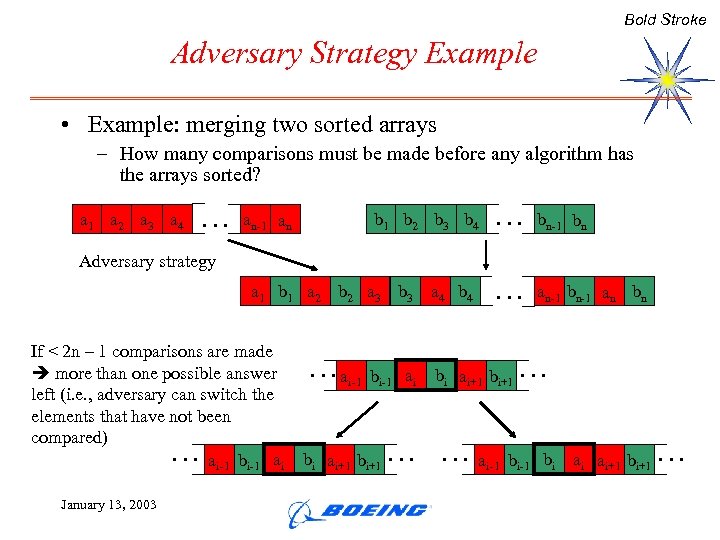
Bold Stroke Adversary Strategy Example • Example: merging two sorted arrays – How many comparisons must be made before any algorithm has the arrays sorted? a 1 a 2 a 3 a 4 … b 1 b 2 b 3 b 4 an-1 an Adversary strategy a 1 b 1 a 2 b 2 a 3 b 3 If < 2 n – 1 comparisons are made more than one possible answer left (i. e. , adversary can switch the elements that have not been compared) ai-1 bi-1 ai … January 13, 2003 …a i-1 bi-1 ai bi ai+1 bi+1 a 4 b 4 … bn-1 bn … an-1 bn-1 an bn bi ai+1 bi+1 … …a i-1 … bi-1 bi ai ai+1 bi+1 …

Bold Stroke On-Line/Dynamic Algorithms • Algorithms that don’t have knowledge of future requests/input – Compare to off-line algorithms that have complete knowledge of input – Provable bound compared to off-line solution • Examples: Ski rental vs. purchase, scheduling jobs with deadlines using EDF, B = cost to buy R = cost to rent Can have 2 -competitive algorithm, i. e. , provable 2 B bound on cost January 13, 2003

Bold Stroke Conclusion • Techniques exist for: – Provable poly-time algorithms – Determining unlikely poly-time algorithms – Next best solutions with provable bounds • When to use what technique – Mostly developed through practice and intuition • What does it matter? – Provable solutions January 13, 2003
0916f832ddb1f41c1dbebec25ebc4033.ppt