BNFO 602 Phylogenetics –maximum parsimony Usman Roshan
Why phylogenetics? • Study of evolution – Origin and migration of humans – Origin and spead of disease • Many applications in comparative bioinformatics – Sequence alignment – Motif detection (phylogenetic motifs, evolutionary trace, phylogenetic footprinting) – Correlated mutation (useful for structural contact prediction) – Protein interaction – Gene networks – Vaccine devlopment – And many more…
Maximum Parsimony • Character based method • NP-hard (reduction to the Steiner tree problem) • Widely-used in phylogenetics • Slower than NJ but more accurate • Faster than ML • Assumes i. i. d.
Maximum Parsimony • Input: Set S of n aligned sequences of length k • Output: A phylogenetic tree T – leaf-labeled by sequences in S – additional sequences of length k labeling the internal nodes of T such that is minimized.
Maximum parsimony (example) • Input: Four sequences – ACT – ACA – GTT – GTA • Question: which of the three trees has the best MP scores?
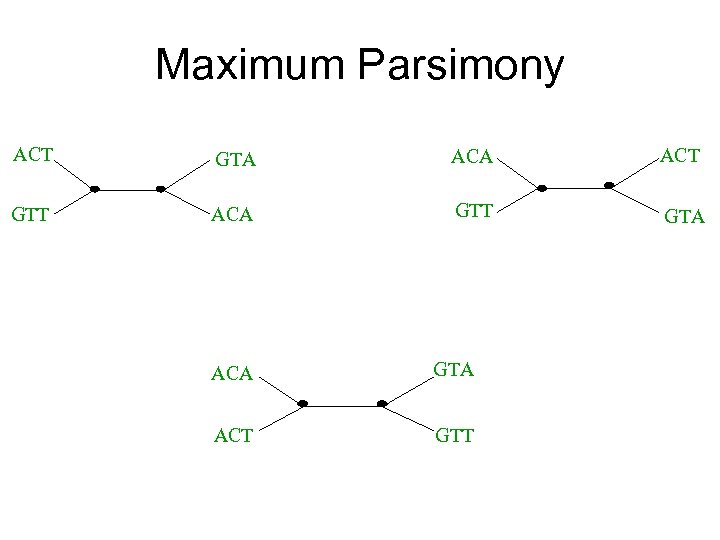
Maximum Parsimony ACT GTA ACT GTT ACA GTT GTA ACA GTA ACT GTT
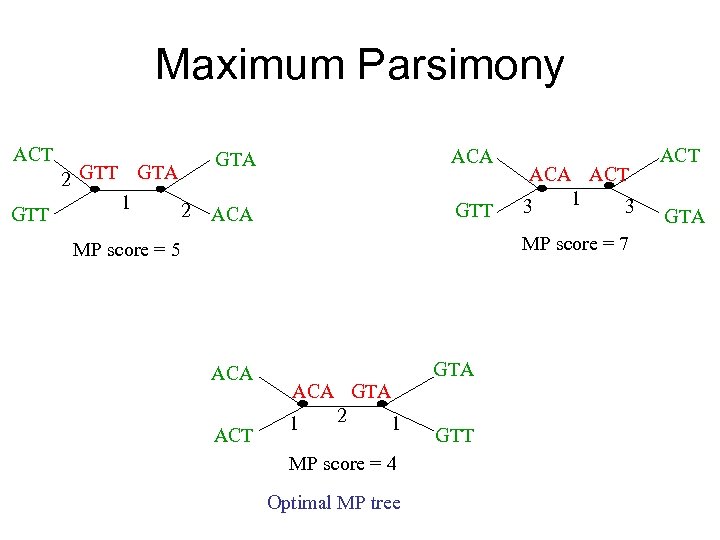
Maximum Parsimony ACT GTT 2 GTT GTA 1 2 GTA ACA GTT ACA ACT 1 3 3 MP score = 7 MP score = 5 ACA ACT GTA ACA GTA 2 1 1 MP score = 4 Optimal MP tree GTT ACT GTA
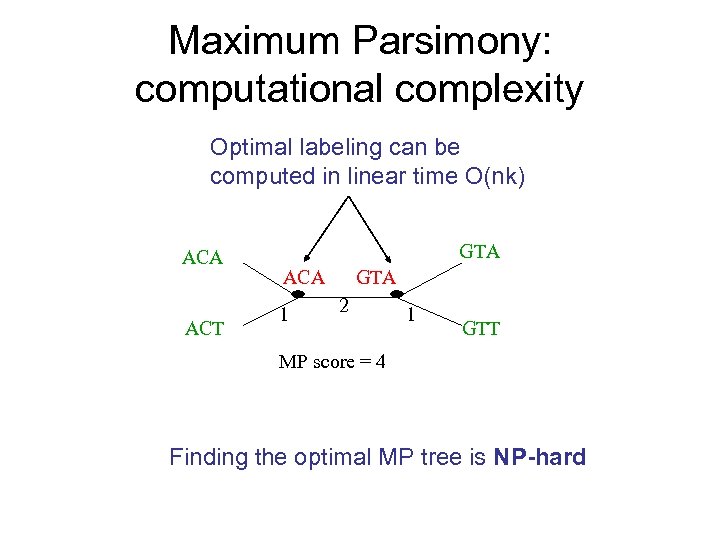
Maximum Parsimony: computational complexity Optimal labeling can be computed in linear time O(nk) ACA ACT GTA ACA 1 GTA 2 1 GTT MP score = 4 Finding the optimal MP tree is NP-hard
Local search strategies Local optimum Cost Global optimum Phylogenetic trees
Local search for MP • Determine a candidate solution s • While s is not a local minimum – Find a neighbor s’ of s such that MP(s’)<MP(s) – If found set s=s’ – Else return s and exit • Time complexity: unknown---could take forever or end quickly depending on starting tree and local move • Need to specify how to construct starting tree and local move
Starting tree for MP • Random phylogeny---O(n) time • Greedy-MP
Greedy-MP takes O(n^2 k^2) time
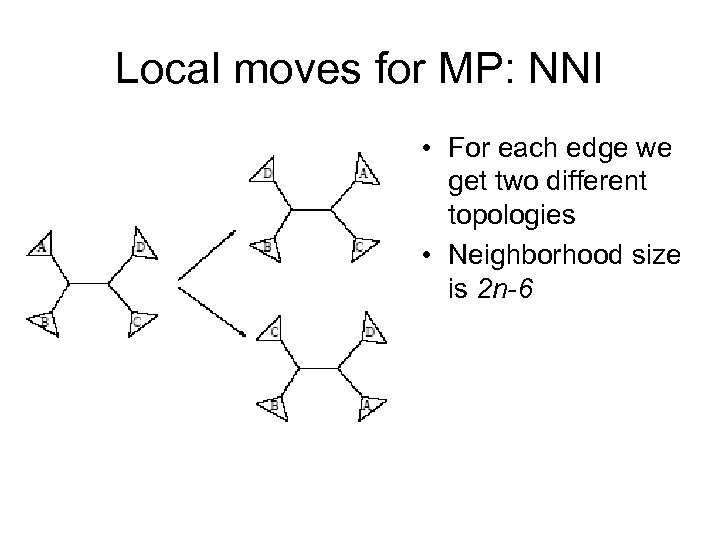
Local moves for MP: NNI • For each edge we get two different topologies • Neighborhood size is 2 n-6
Local moves for MP: SPR • Neighborhood size is quadratic in number of taxa • Computing the minimum number of SPR moves between two rooted phylogenies is NP-hard
Local moves for MP: TBR • Neighborhood size is cubic in number of taxa • Computing the minimum number of TBR moves between two rooted phylogenies is NP-hard
Local optima is a problem
Iterated local search: escape local optima by perturbation Local search Local optimum
Iterated local search: escape local optima by perturbation Local search Local optimum Perturbation Output of perturbation
Iterated local search: escape local optima by perturbation Local search Local optimum Perturbation Local search Output of perturbation
ILS for MP • Ratchet (Nixon 1999) • Iterative-DCM 3 (Roshan et. al. 2004) • TNT (Goloboff et. al. 1999)
Скачать презентацию BNFO 602 Phylogenetics maximum parsimony Usman Roshan
9e57960fe840ee3b5e3f966987307d98.ppt