Lecture.ppt
- Количество слайдов: 68

БМС –Биомедстатистика kafmedinform@gmail. com 1

Лекция 2. Статистический анализ медицинских данных Ekaterina. delakova@gmail. com 2

Сравнение и анализ выборочных данных • Эффект от терапии • Исследования случай-контроль • Сравнение групп. . . . . 3

Сравнение результатов обследования пациентов. Влияет ли наличие диабета на показатели состояния здоровья человека? 2 группы людей. Случай – наличие заболевания Контроль: отсутствие заболевания Измерили показатели, сравнили, Выводы? 4

Основные задачи и проблемы Аналитической Статистики • • • Статистическое оценивание (параметров) Оценки точечные и интервальные Проверка статистических гипотез и (или) Сравнение моделей Анализ статистических связей Корреляция и регрессия 5

Статистические меры и их предназначение • Бейзов фактор (BF – Bayes Factor) → сравнение моделей и (или) гипотез • P-значение → проверка статистической значимости нулевой гипотезы • Размер эффекта (ES – Effect Size) → практическая (клиническая) значимость • Доверительные интервалы для размера эффекта → визуализация результатов 6

Задача • Человек подбросил монету 10 раз, и все 10 раз монета выпала вверх одной стороной (например, орлом): yнабл= 10. • Вопрос: • Что можно сказать обо мне или о монете: • Можно ли признать монету правильной (идеальной)? • Или монета фальшивая? • Честный ли нам попался человек, везучий ли, или ловкач, или жулик? • Если монета недоступна для непосредственного осмотра, то задача неизбежно становится вероятностатистической. 7

Бейзовская логика - I • Две модели: • M 1 – монета идеальная (правильная), т. е. параметр Модели 1: • = Pr(орел) = 1/2. • M 2 – монета фальшивая – с обеих сторон орел, т. е. параметр Модели 2: • = Pr(орел) = 1. • Вопрос: какая из двух моделей более правдоподобна, если yнабл. = 10? 8

Бейзовская логика – I (продолжение) • • • Модель M 1 – монета идеальная и игрок честный. Модель M 2 – монета фальшивая или игрок ловкач и жулик. Такие функции называются функциями правдоподобия. Кратко – правдоподобия. Они выражают, насколько правдоподобно каждое конкретное значение параметра при условии, что мы получили наблюдаемое значение yнабл. 9

Бейзовская логика – I (продолжение) • Отношение правдоподобий (Бейзов множитель, Бейзов фактор) • В 1024 раза более правдоподобно (вероятно, реально) получить наблюдаемый результат (10 орлов подряд), если верна Модель 2 ( = 1) – монета фальшивая, нежели если верна Модель 1 ( = 1/2) – монета идеальная и игрок честен. 10

Бейзовская логика - II • Модель 3: неопределенная: • Принцип недостаточного основания (Лаплас): вероятностная переменная (вероятность выпадения орла) распределена равномерно на отрезке от 0 до 1: • В 93 раза более правдоподобно получить наблюдаемый результат • при условии, что (Модель 3) нежели при (Модель 1). 11

Бейзовская логика - III • Сравнение Модели 2 и Модели 3: • В 11 раз более правдоподобно получить наблюдаемый результат (n =10, y = 10) при условии, что монета фальшивая, т. е. = 1 (Модель 2), нежели при неопределенности (Модель 3). 12
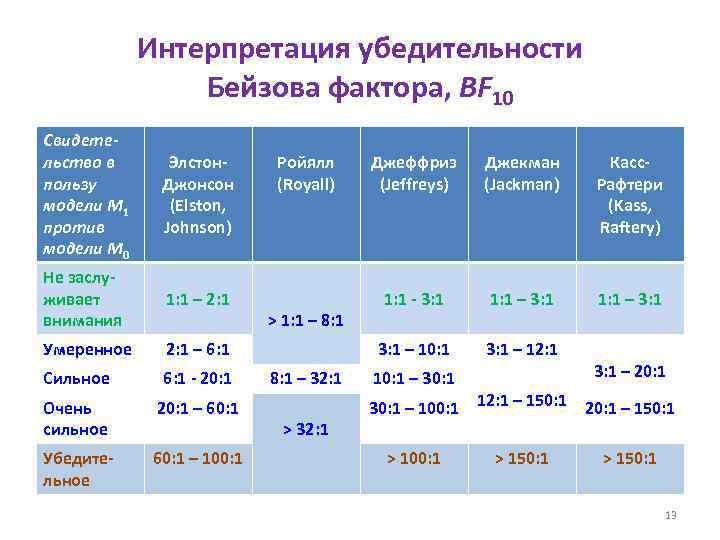
Интерпретация убедительности Бейзова фактора, BF 10 Свидетельство в пользу модели M 1 против модели M 0 Элстон. Джонсон (Elston, Johnson) Не заслуживает внимания 1: 1 – 2: 1 Умеренное 2: 1 – 6: 1 Сильное 6: 1 - 20: 1 Очень сильное 20: 1 – 60: 1 Убедительное 60: 1 – 100: 1 Ройялл (Royall) 8: 1 – 32: 1 > 32: 1 Джекман (Jackman) Касс. Рафтери (Kass, Raftery) 1: 1 - 3: 1 1: 1 – 3: 1 – 10: 1 > 1: 1 – 8: 1 Джеффриз (Jeffreys) 3: 1 – 12: 1 10: 1 – 30: 1 3: 1 – 20: 1 30: 1 – 100: 1 12: 1 – 150: 1 20: 1 – 150: 1 > 100: 1 > 150: 1 13

Частотническая логика • Для нашей задачи с выпадением yнабл. =10 орлов при n=10 подбрасываниях (испытаниях) • Модель: • Выдвигаем две гипотезы: • Нулевая гипотеза H 0: монета идеальная (и игрок честный), т. е. =1/2 • Альтернативная гипотеза H 1: ≠ 1/2 • Вычисляем вероятность, называемую • P-значением. 14

Влияет • • ли ли наличие диабета на показатели состояния здоровья человека? Частотническая логика Нулевая гипотеза – презумкция невиновности. Выдвигаем нулевую гипотезу: различий в выборках нет. Альтернативная гипотеза различия в выборках есть (статистически значимы). Начинаем «собирать доказательства» 15

Р-значение • P-значение есть условная вероятность, а именно: • Вероятность получить наблюдаемые данные D и еще менее вероятные (или еще более отклоняющиеся от ожидаемых) • ПРИ УСЛОВИИ, • что верна нулевая гипотеза H 0. • Pval = Pr{|D| ≥ |dнабл. ||H 0} • Заметим, что «еще менее вероятные данные» не являются «данными» , мы их не наблюдаем. • Мы их додумываем из всех возможных значений в рамках выбранной нами (нулевой) модели. 16

Наблюдаемое P-значение • Если монета правильная (и игрок честный), то наблюдаемое P-значение • Оно малó, и это дает нам основание сомневаться в нулевой гипотезе • Скорее всего, верна альтернативная гипотеза H 1, т. е. . Скорее всего 17

Сжатие (свертка, редукция) статистических данных • Статистика – любая функция от вероятностных переменных, порождающих статистические данные. • Простейший пример - выборочное среднее: • Оно порождается вероятностной переменной: 18
Поиск различий 19
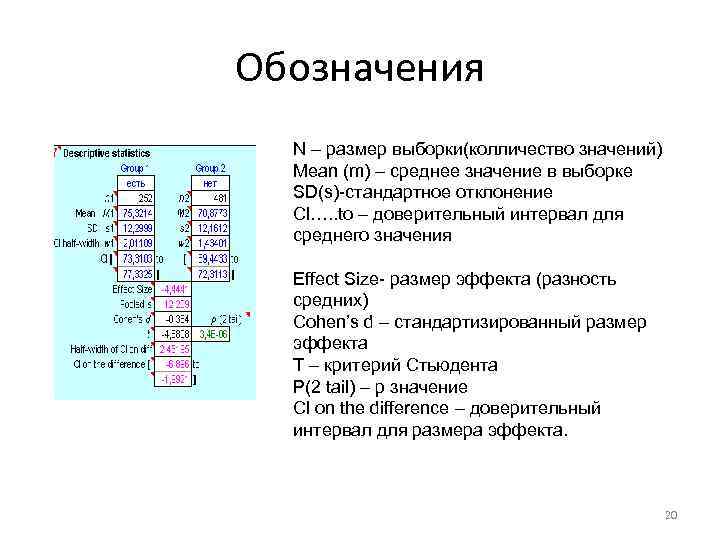
Обозначения N – размер выборки(колличество значений) Mean (m) – среднее значение в выборке SD(s)-стандартное отклонение Cl…. . to – доверительный интервал для среднего значения Effect Size- размер эффекта (разность средних) Cohen’s d – стандартизированный размер эффекта T – критерий Стьюдента P(2 tail) – p значение Cl on the difference – доверительный интервал для размера эффекта. 20

Статистики критериев (тестовые статистики) • Тестовая статистика – статистика, используемая для проверки конкретной статистической гипотезы. • Пример: статистика t-критерия Стьюдента • В этом случае проверка гипотезы H 0 о равенстве двух средних: H 0: M 1 – M 2 = 0 сводится к проверке гипотезы о том, что t = 0. • Когда эта нулевая гипотеза верна, то распределение этой статистики известно – это t-распределение Стьюдента с параметром (числом степеней свободы), равным df. 21

Р-значение • Тогда P-значение есть: • Вероятность получить наблюдаемое значение tнабл. статистики t-критерия и все остальные, еще менее вероятные значения этой статистики (или значения, еще более отклоняющиеся от ожидаемого) ПРИ УСЛОВИИ, что верна нулевая гипотеза H 0: • Pval = Pr[|T| ≥ |tнабл. | | H 0]. • Еще раз следует обратить внимание на то, что «еще менее вероятные значения статистики критерия» мы не наблюдаем. • Мы их додумываем из всех возможных значений в рамках выбранной нами (нулевой) модели. 22

Интерпретация малых P-значений • Когда мы получаем малое P-значение, возможно несколько объяснений: • 1. Удивление, неожиданность: свершилось маловероятное (неожидаемое) событие, которое в следующий раз при повторении эксперимента, не произойдет, т. е. результат не воспроизведется. • 2. Нулевая гипотеза H 0 неверна, т. е. ≠ ½. • 3. Неверна (неадекватна) наша (нулевая) модель M 0: выборочные наблюдения подчиняются не биномиальному, а какому-то иному распределению. • 4. Неверны обе: и модель, и гипотеза. 23

Визуализация результатов проверки статистических гипотез с помощью доверительных интервалов для размера эффекта 24

Доверительный интервал • Доверительный интервал - это допустимое отклонение наблюдаемых значений от истинных. Размер этого допущения определяется исследователем с учетом требований к точности информации. Если увеличивается допустимая ошибка, размер выборки уменьшается, даже если уровень доверительной вероятности останется равным 95%. • Доверительный интервал показывает, в каком диапазоне расположатся результаты выборочных наблюдений 25
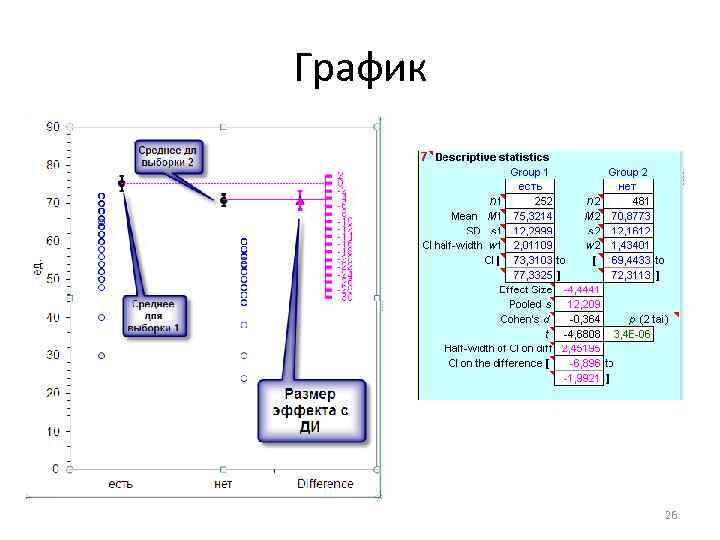
График 26

Выбор порога для P-значения, и возможен ли он? • Когда наблюдаемое P-значение мало, появляется (внестатистическое, интуитивнологическое) основание (соблазн) отвергнуть H 0. • Однако нет никаких статистических соображений, какое значение P следует считать настолько малым, чтобы смело отвергнуть H 0. • Это решение является внестатистическим. • На практике решение отклонить или принять H 0 должно зависеть от обстоятельств. • Исследователь в каждой конкретной ситуации должен сам делать этот выбор. 27

Уровни значимости, α • 0, 05 • 0, 01 • 0, 001 • Их выбор – всеобщая договоренность 28

Гипноз цифр 0, 05 и 95% • Наиболее часто в качестве критического порога используется уровень значимости α = 0, 05. • Преодоление этого порогового уровня (Pval < 0, 05) всего лишь в одной выборке считается достаточным для решения отклонить нулевую гипотезу и для вывода о статистической значимости наблюдаемого эффекта. • В последнем случае часто употребляется даже более сильное утверждение: «эффект достоверен» . 29
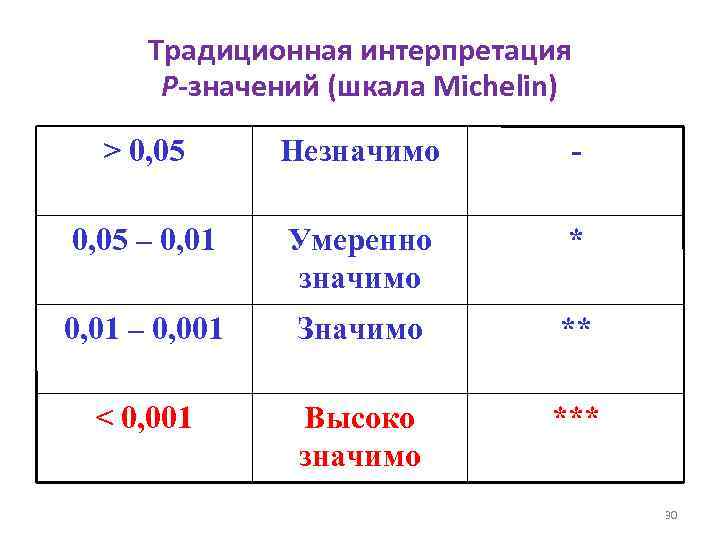
Традиционная интерпретация P-значений (шкала Michelin) > 0, 05 Незначимо - 0, 05 – 0, 01 Умеренно значимо * 0, 01 – 0, 001 Значимо ** < 0, 001 Высоко значимо *** 30
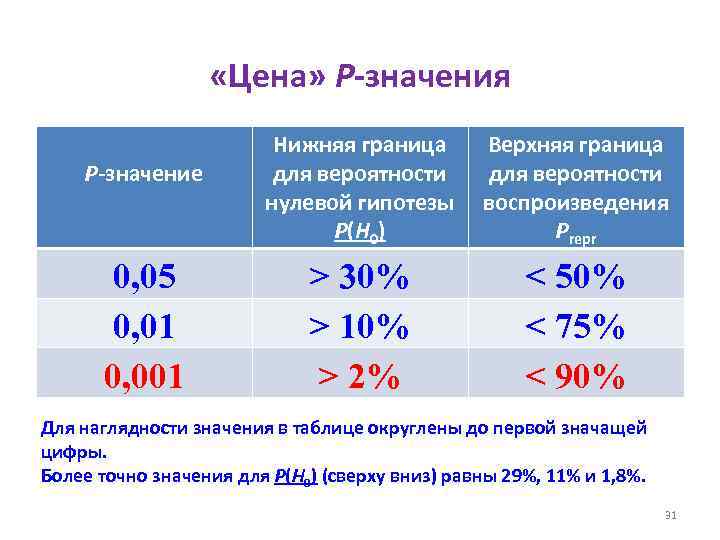
«Цена» Р-значения P-значение 0, 05 0, 01 0, 001 Нижняя граница Верхняя граница для вероятности нулевой гипотезы воспроизведения P(H 0) Рrepr > 30% > 10% > 2% < 50% < 75% < 90% Для наглядности значения в таблице округлены до первой значащей цифры. Более точно значения для P(H 0) (сверху вниз) равны 29%, 11% и 1, 8%. 31

Повторение – мать познания • Повторение составляет суть науки: • ученый должен всегда задумываться о том, что произойдет, если он или другой ученый повторят его эксперимент (Guttman, 1977). • Ученые разработали метод определения надежности (валидности) своих результатов. • Они научились задавать вопрос: воспроизводимы ли они? (Scherr, 1983). 32

Статистическая значимость и размер эффекта • Эффект (различие, связь, риск, польза, ассоциация и т. п. ) может быть статистически значимым, но его практическая (например, клиническая) ценность может оказаться ничтожной. • «Статистически значимый» не означает «значительный» , «практически важный» , «ценный» . • Эффекты могут быть реальными, неслучайными, но, тем не менее, очень (пренебрежимо) маленькими. 33

Размер эффекта • Вопрос о клинической (практической) ценности (важности) наблюдаемого • Размера Эффекта • является ключевым при интерпретации результатов биомедицинских исследований (например, клинических испытаний). • Абсолютный и • Стандартизированный (безразмерный) 34
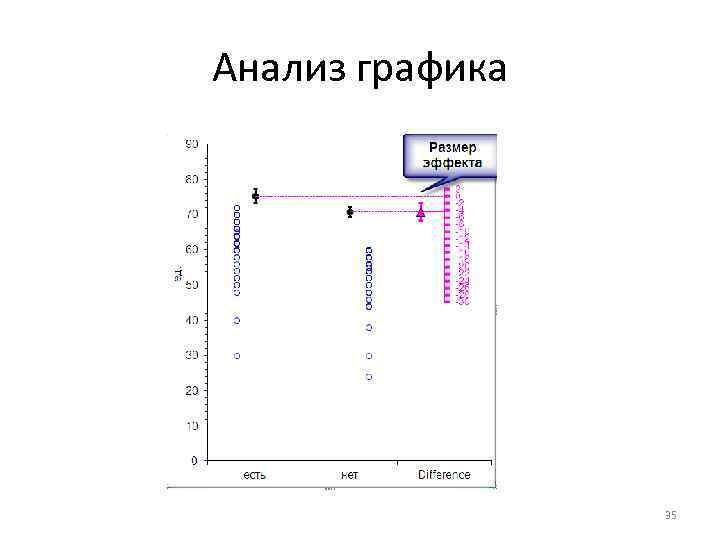
Анализ графика 35

Стандартизированный размер эффекта по Коэну (Cohen) d. C 36
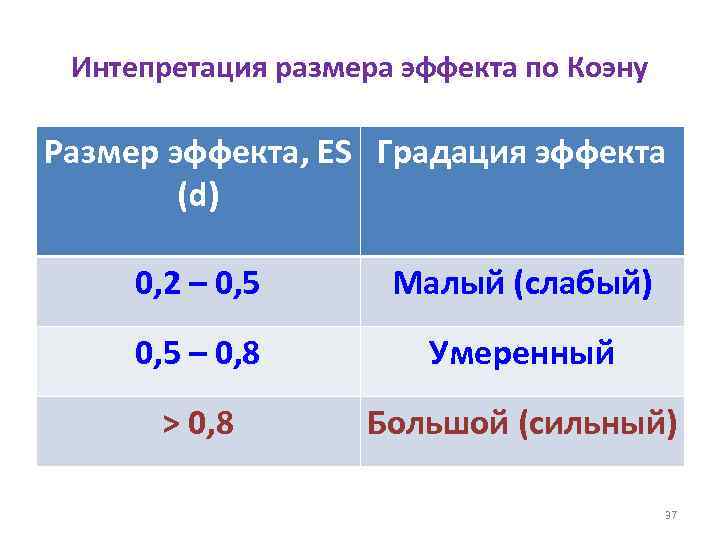
Интепретация размера эффекта по Коэну Размер эффекта, ES Градация эффекта (d) 0, 2 – 0, 5 Малый (слабый) 0, 5 – 0, 8 Умеренный > 0, 8 Большой (сильный) 37

Интерпретация размера эффекта по Хопкинсу (Hopkins) http: //www. sportsci. org/resource/stats/ Размер эффекта, ES 0 – 0, 2 – 0, 6 – 1, 2 – 2, 0 – 4, 0 - Градация эффекта Ничтожный Малый (слабый) Умеренный Большой (сильный) Очень большой Абсолютный 38

Наглядное представление (визуализация) и контроль качества статистических данных 39

Проверка согласия с нормальным (гауссовым) распределением ID N = 50 Критерий: Шапиро-Уилка (Shapiro-Wilk) W = 0, 92 p(normal) 0, 0028 Жарка-Бера (Jarque-Bera) JB = 14, 7 p(normal) 0, 00064 • Распределение данных плохо согласуется с гауссовым (нормальным) и мы можем взять на себя смелость признать наблюдаемое отклонение статистически значимым (P = 0, 0028; 0, 00064; 0, 0068) Монте-Карло p(Monte Carlo) 0, 0068 40

Программа Instat+ http: //www. rdg. ac. uk/ssc/software/instat. htm l 41
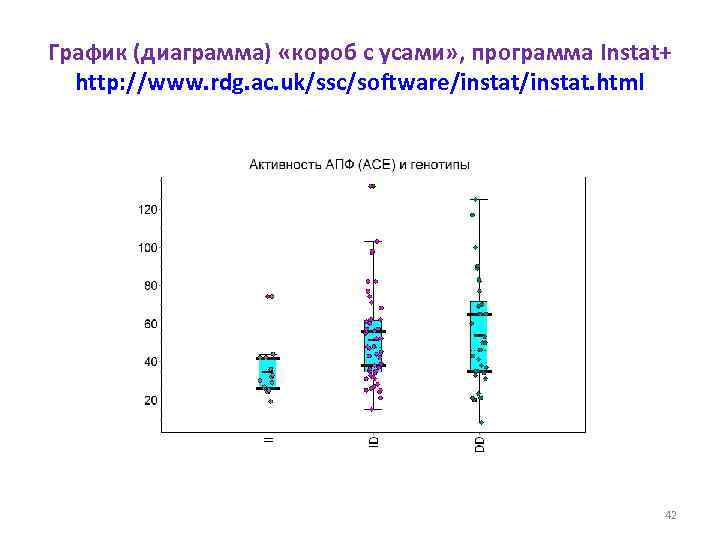
График (диаграмма) «короб с усами» , программа Instat+ http: //www. rdg. ac. uk/ssc/software/instat. html 42

Резко выделяющиеся (выскакивающие) значения – «выбросы» • Выскакивающие значения можно и нужно выявлять. • Но отбрасывать их следует на основе внестатистических соображений. • Например, если записано значение для артериального давления 1100, то очевидно, что здесь опечатка: лишняя 1 или лишний 0. 43

Типы интервальных оценок • : • Доверительные интервалы (интервалы накрытия) • Правдоподобные (бейзовские) интервалы • Предсказательные интервалы 44

Сравнение групп гомозигот II и DD, 1 -α = 0, 95. Программа ESCI JSMS. xls http: //www. latrobe. edu. au/psy/esci/ 45
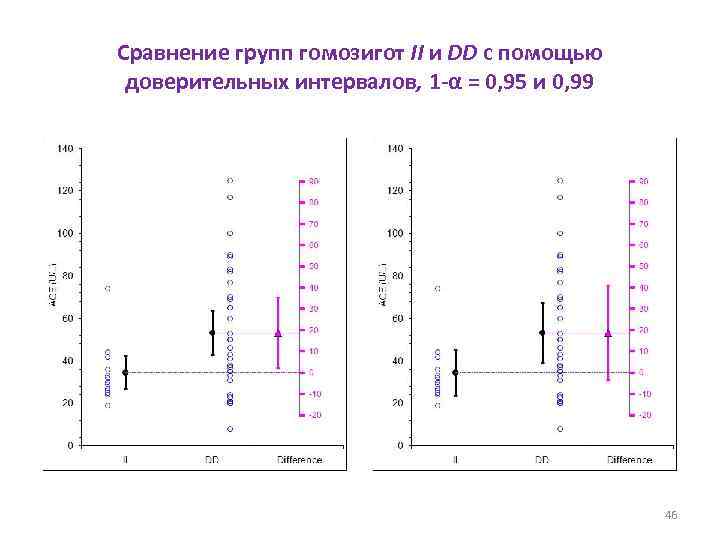
Сравнение групп гомозигот II и DD с помощью доверительных интервалов, 1 -α = 0, 95 и 0, 99 46

Сравнение групп гомозигот II и гетерозигот ID, 1 -α = 0, 95 47
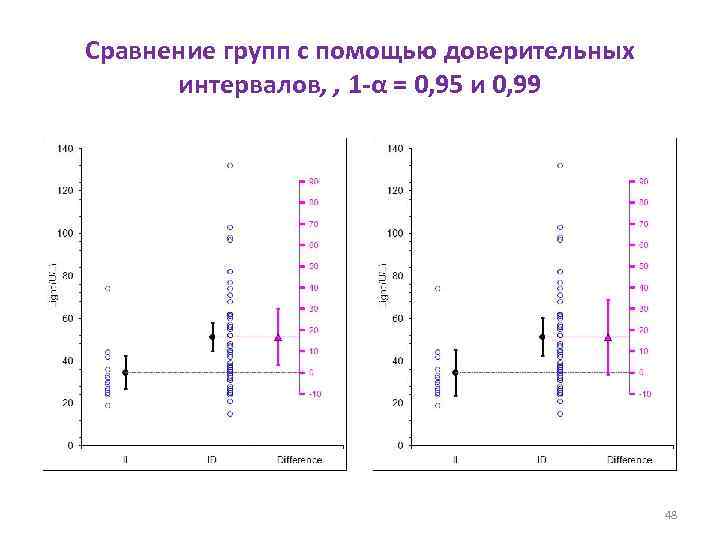
Сравнение групп с помощью доверительных интервалов, , 1 -α = 0, 95 и 0, 99 48
Бейзов фактор, программа Bayes Factor Calculators http: //pcl. missouri. edu/bayesfactor 49
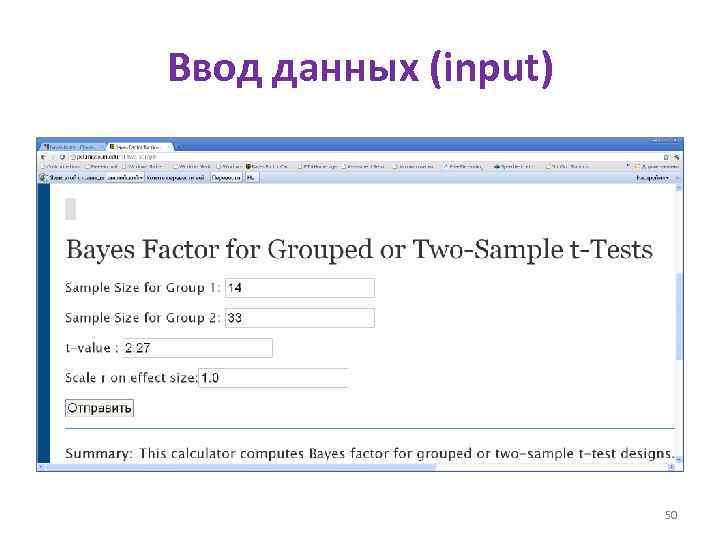
Ввод данных (input) 50

Вывод результатов (output) • • Всго лишь в 2 -3 раза более прадоподобно получить наблюдаемые различия (ES = = 18, 8 U/L) между сравниваемыми группами при условии, что верна гипотеза H 1: 0, нежели при условии, что верна гипотеза H 0: = 0. Такое значение BF 01 общепринято интерпретировать как не заслуживающее внимания. А стандартизированный размер эффекта (d. C=0, 72) можно интерпретировать как умеренный. 51

Ошибки I и II рода и мощность статистического критерия 52
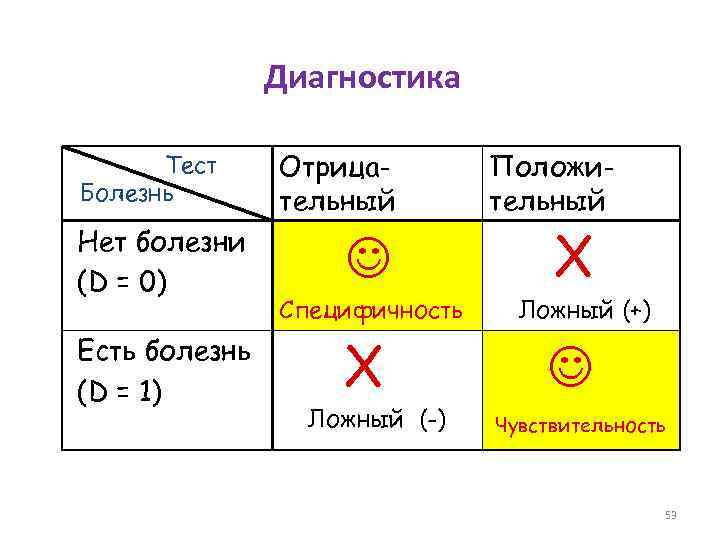
Диагностика Тест Болезнь Нет болезни (D = 0) Есть болезнь (D = 1) Отрицательный Специфичность X Ложный (-) Положительный X Ложный (+) Чувствительность 53
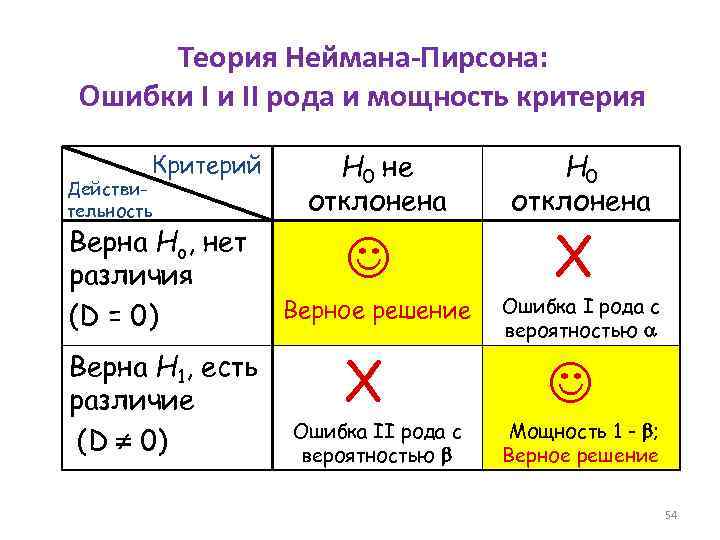
Теория Неймана-Пирсона: Ошибки I и II рода и мощность критерия Критерий Действительность Верна Ho, нет различия (D = 0) Верна H 1, есть различие (D 0) H 0 не отклонена Верное решение X Ошибка II рода с вероятностью H 0 отклонена X Ошибка I рода с вероятностью Мощность 1 - ; Верное решение 54

Компромисс • Например, в случае металлодетектора • повышение чувствительности прибора приведёт к увеличению риска ошибки первого рода (ложная тревога), а • понижение чувствительности - к увеличению риска ошибки второго рода (пропуск запрещённого предмета). 55

Мощность статистического критерия • Мощность статистического критерия есть вероятность того, что критерий правильно отклонит ложную нулевую гипотезу (правильно примет верную альтернативную гипотезу). • Традиционно ее обозначают (1 – β), где β - вероятность ошибки II рода. • Чем больше мощность критерия, тем меньше вероятность совершить ошибку II рода. 56

Мощность статистического критерия • Мощность статистического критерия измеряет способность критерия выявлять истинные различия (эффекты). • Или: способность приводить к правильному решению принять альтернативную гипотезу, т. е. принять ее, когда она действительно верна. • Ее можно интерпретировать как чувствительность критерия к отклонениям от условий нулевой гипотезы. 57
Программа G*Power http: //www. psycho. uni-duesseldorf. de/aap/projects/gpower/ 58

Анализ мощности a priori или post-hoc • Анализ мощности можно проводить либо a priori, т. е. до получения данных, либо post hoc, т. е. после получения данных. • A priori анализ мощности обычно используется для оценки объема выборки N, необходимого для достижения приемлемой мощности. • Post hoc анализ мощности используется для оценки достигнутой мощности. • При этом предполагается, что наблюдаемый эффект и его варьирование равны истинным значениям параметров. 59

• A priori – лат. «независимо от опыта, до опыта» . • Post hoc – лат. «после этого» , сокращенно от Post hoc ergo propter hoc - «после этого, поэтому вследствие этого» . • Post hoc мощность – наблюдаемая мощность, достигнутая мощность. 60
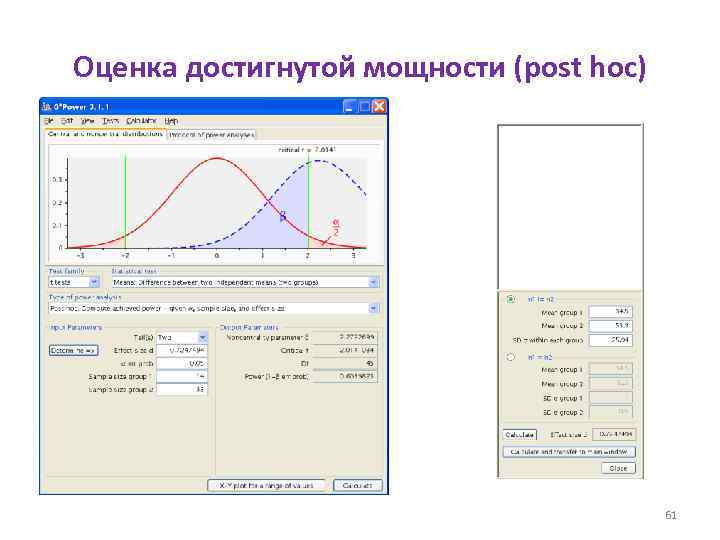
Оценка достигнутой мощности (post hoc) 61

Элементы планирования эксперимента 62

Программа G*Power http: //www. psycho. uni-duesseldorf. de/abteilungen/aap/gpower 3 • Оценка a priori минимально необходимого объема выборки N для достижения статистически значимого отличия наблюдаемой доли от ожидаемого значения при заданных уровне значимости α и мощности (1 – β) 63
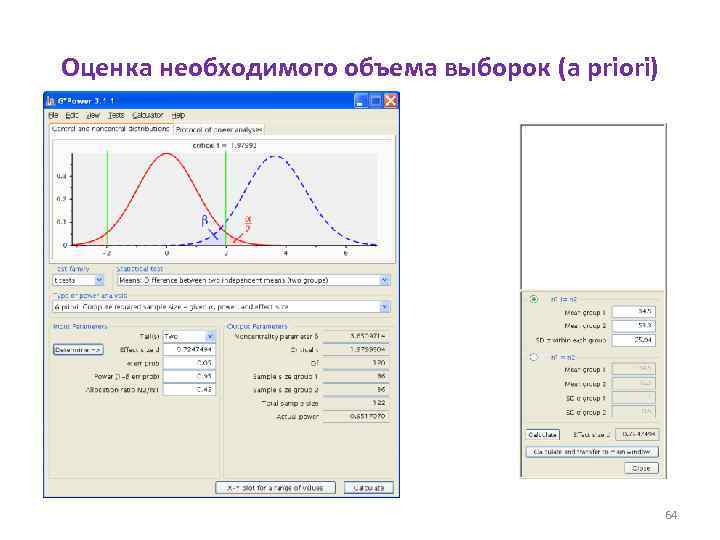
Оценка необходимого объема выборок (a priori) 64

Значение вероятностной P-величины • P-значение есть наблюдаемое значение соответствующей вероятностной переменной • Всякий раз мы наблюдаем одно из ее возможных значений. • Когда H 0 верна, Pval имеет (непрерывное) равномерное распределение на отрезке [0; 1]. 65

• Отсюда следует, что, строго говоря, на снове всего лишь одного изолированного исследования нельзя делать определенные выводы. • Любое научное исследование должно повторяться многократно, и должна исследоваться воспроизводтмость результатов. 66

Отчет должен содержать Постановка задачи Расчет в программе ESCI График из программы ESCI Выводы! Ef, ДИ для Ef, t-статистика, pзначение • Главный вопрос: есть ли статистически значимые различия в выборках? • • 67

Задачи • Практика 2. Программы 68
Lecture.ppt