eaf0e194b06aaa0da0483b08bffa3863.ppt
- Количество слайдов: 73

BLIND SOURCE SEPARATION BY KURTOSIS MAXIMIZATION WITH APPLICATIONSIN WIRELESS COMMUNICATIONS Chong-Yung Chi (祁忠勇 ) Institute of Communications Engineering & Department of Electrical Engineering National Tsing Hua University Hsinchu, Taiwan 30013, R. O. C. Tel: +886 -3 -5731156, Fax: +886 -3 -5751787 E-mail: cychi@ee. nthu. edu. tw http: //www. ee. nthu. edu. tw/cychi/ Invited talk at I 2 R, Singapore, July 18, 2006. Acknowledgments: The viewgraphs were prepared through Chun-Hsien Peng’s helps.

OUTLINE 1. Introduction to Blind Source Separation ( BSS) 2. FKMA and MSC Procedure 3. Turbo Source Extraction Algorithm ( TSEA) 4. Non-cancellation Multistage Source ( NCMS) Separation Algorithms NCMS-FKMA NCMS-TSEA 5. Simulation. Results --- Part 1 6. Turbo Space-time Receiver for CCI/ISI Reduction 7. Simulation. Results --- Part 2 8. Conclusions FKMA: Fast Kurtosis Maximization Algorithm MSC: Multistage Successive Cancellation 1
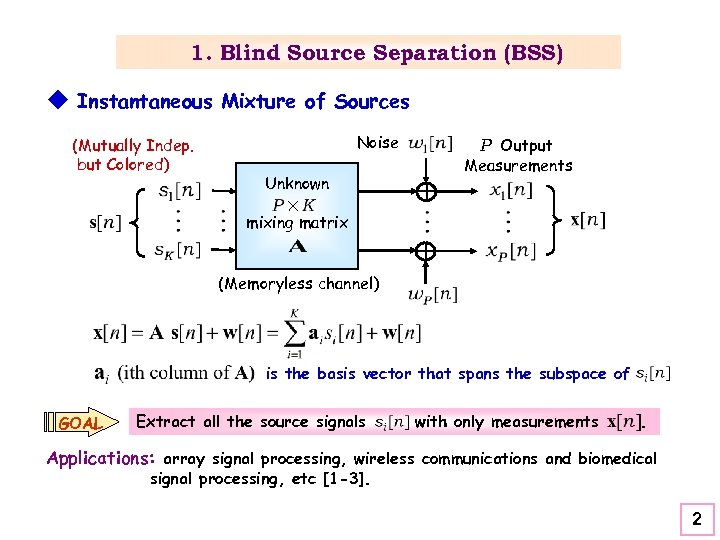
1. Blind Source Separation (BSS) u Instantaneous Mixture of Sources (Mutually Indep. but Colored) Noise Unknown P Output Measurements mixing matrix (Memoryless channel) is the basis vector that spans the subspace of GOAL Extract all the source signals with only measurements . Applications: array signal processing, wireless communications and biomedical signal processing, etc [1 -3]. 2
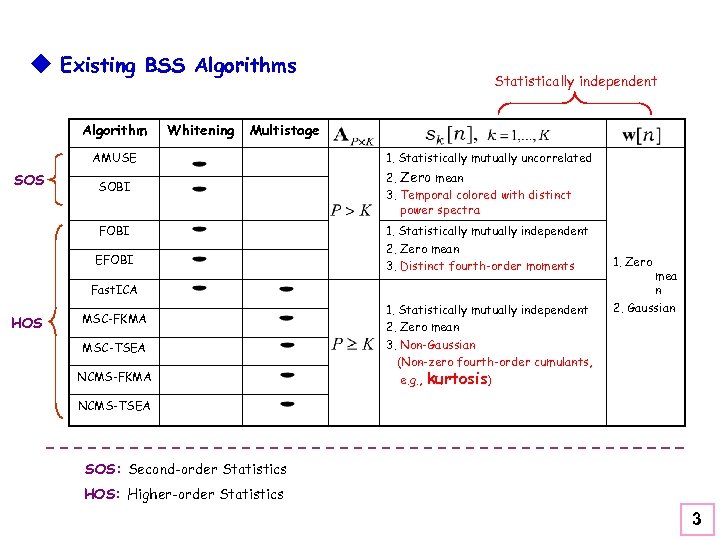
u Existing BSS Algorithms Algorithm Whitening Multistage AMUSE SOS Statistically independent SOBI FOBI EFOBI 1. Statistically mutually uncorrelated 2. Zero mean 3. Temporal colored with distinct power spectra 1. Statistically mutually independent 2. Zero mean 3. Distinct fourth-order moments Fast. ICA HOS MSC-FKMA MSC-TSEA NCMS-FKMA 1. Statistically mutually independent 2. Zero mean 3. Non-Gaussian (Non-zero fourth-order cumulants, e. g. , 1. Zero mea n 2. Gaussian kurtosis) NCMS-TSEA SOS: Second-order Statistics HOS: Higher-order Statistics 3
![AMUSE: Algorithm for Multiple Unknown Signals Extraction (Tong et al. , 1990 [1]) SOBI: AMUSE: Algorithm for Multiple Unknown Signals Extraction (Tong et al. , 1990 [1]) SOBI:](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-5.jpg)
AMUSE: Algorithm for Multiple Unknown Signals Extraction (Tong et al. , 1990 [1]) SOBI: Second-order Blind Identification (Belouchrani et al. , 1997 [2]) FOBI: Fourth-order Blind Identification (Cardoso, 1989 [12]) EFOBI: Extended Fourth-order Blind Identification (Tong et al. , 1991 [1]) Fast. ICA: Fast Independent Component Analysis (Hyvarinen et al. , 1997 [13, 14]) MSC: Multistage Successive Cancellation NCMS: Non-cancellation Multistage FKMA: Fast Kurtosis Maximization Algorithm TSEA: Turbo Source Extraction Algorithm 4

u AMUSE and SOBI Algorithm Using SOS: Step 1: Prewhitening by Eigenvalue Decomposition (EVD) (Px. P matrix) EVD Þ{ : largest K eigenvalues of : associated K eignevectors of : average of the other (smallest) P-K eigenvalues of (assuming that ) (whitening matrix) : Kx. K unitary matrix (dimension-reduced whitening spatial processing) AMUSE: Algorithm for Multiple Unknown Signals Extraction (Tong et al. , 1990 [1]) SOBI: Second-order Blind Identification (Belouchrani et al. , 1997 [2]) 5
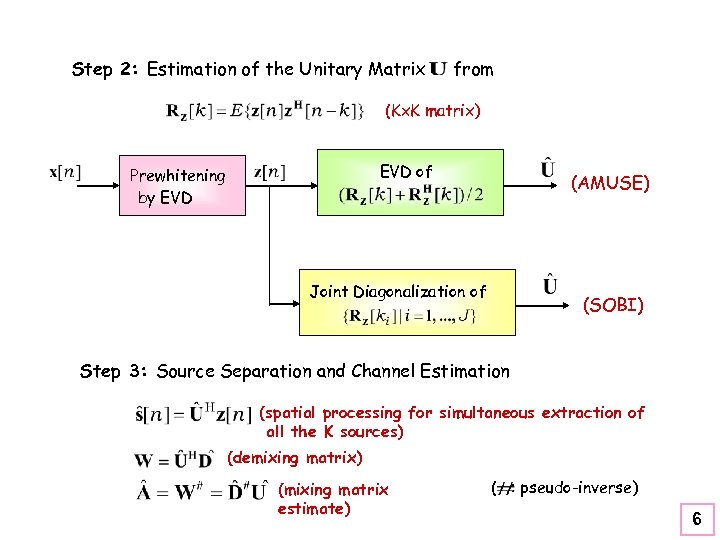
Step 2: Estimation of the Unitary Matrix from (Kx. K matrix) EVD of Prewhitening by EVD (AMUSE) Joint Diagonalization of (SOBI) Step 3: Source Separation and Channel Estimation (spatial processing for simultaneous extraction of all the K sources) (demixing matrix) (mixing matrix estimate) ( : pseudo-inverse) 6

2. FKMA and MSC Procedure u Assumptions: (A 1) The unknown (A 2) mixing matrix is of full column rank with . are modeled as Stable LTI System (A 3) : zero-mean non-Gaussian independent identically distributed (i. i. d. ) process with ; is statistically independent of for all. is zero-mean Gaussian and statistically independent of. : fourth-order joint cumulant of random variables (referred to as kurtosis of ) FKMA: Fast Kurtosis Maximization Algorithm (Chi and Chen, 2001 [4, 5]) MSC: Multistage Successive Cancellation 7

u Definition of HOS (i. e. , Cumulants): (Bartlett, 1955, Brillinger, 1975, etc) where is the characteristic function of random variables Assume that are zero-mean random variables. Then (referred to as kurtosis of ) 8
![u Fast Kurtosis Maximization Algorithm (FKMA) Criterion [7]: Maximization magnutude of normalized kutorsis of u Fast Kurtosis Maximization Algorithm (FKMA) Criterion [7]: Maximization magnutude of normalized kutorsis of](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-10.jpg)
u Fast Kurtosis Maximization Algorithm (FKMA) Criterion [7]: Maximization magnutude of normalized kutorsis of l Closed-form solution for (Chi et al. , 2001 [4, 5]) Optimum (noise-free case) ( is an unknown complex scale factor and ) : Not existent l Gradient-type iterative algorithms for finding a local optimum computationally efficient : Not very where Q is a positive-definite matrix depending on the algorithm used, and μ is the step size such that 9
![u Fast Kurtosis Maximization Algorithm (FKMA) Criterion [7]: Maximization magnutude of normalized kutorsis of u Fast Kurtosis Maximization Algorithm (FKMA) Criterion [7]: Maximization magnutude of normalized kutorsis of](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-11.jpg)
u Fast Kurtosis Maximization Algorithm (FKMA) Criterion [7]: Maximization magnutude of normalized kutorsis of (Chi et al. , 2001 [4, 5]) Optimum (noise-free case) ( is an unknown complex scale factor and ) Algorithm: At the th iteration (SEA) lgorithm ial A nent po ex er Yes Sup Compute ? No (Px. P matrix) To the th iteration Update through a gradient type optimization algorithm such that 9

u Observations: l The FKMA itself is an exclusive spatial processing algorithm. l The smaller the value of , the worse the performance of the FKMA for finite SNR and finite data length. By (A 2) (absolute normalized kurtosis of ) where (entropy measure of the stable sequence ) (equality holds only as , i. e. , minimum entropy of ) can be thought of as a measure of distance of from a Gaussian process, implying that the performance of the FKMA (which requires to be non-Gaussian [6]), depends on. 10
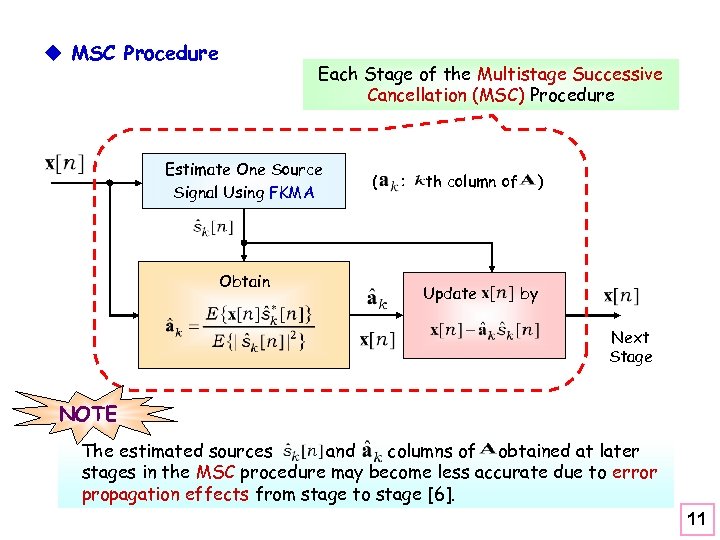
u MSC Procedure Each Stage of the Multistage Successive Cancellation (MSC) Procedure Estimate One Source Signal Using FKMA Obtain ( : th column of Update ) by Next Stage NOTE The estimated sources and columns of obtained at later stages in the MSC procedure may become less accurate due to error propagation effects from stage to stage [6]. 11

3. Turbo Source Extraction Algorithm u Source Separation Filter: (A bank of same temporal filters) where : vector for extracting a colored source signal removing spatial interference due to the mixing matrix , i. e. , . (spatial filter) : single-input single-output (SISO) deconvolution (or higher-order whitening) filter of order to restore from. (temporal filter) u Design Criterion: (Extracted Source) Maximization 12
![Turbo Source Extraction Algorithm (TSEA) (Chi et al. , 2003 [3]) Signal processing procedure Turbo Source Extraction Algorithm (TSEA) (Chi et al. , 2003 [3]) Signal processing procedure](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-15.jpg)
Turbo Source Extraction Algorithm (TSEA) (Chi et al. , 2003 [3]) Signal processing procedure at the th cycle Step 1 Temporal Processing Spatial Processing (b) (a) FKMA(s) Step 1 (b) Step 2 FKMA(t) (a) Step 2 (Extracted Source) 13

Why? Performance of TSEA is superior to FKMA. Interpretations: 1) Temporal Processing : (b) Increasing is equivalent to increasing 2) Spatial Processing: (b) 14

Remarks: l TSEA is computationally efficient with super-exponential convergence rate and P parameters for spatial processing and L+1 parameters for temporal processing, respectively. l The performance gain of the TSEA reaches the maximum as long as the order L (a parameter under our choice) of the temporal filter is sufficiently large. On the other hand, the asymptotic performance of FKMA approaches that of the TSEA as and. l All the sources can be extracted through the MSC procedure. The resultant BSS algorithm that uses the TSEA, is referred to as MSC-TSEA, also outperforms the MSC-FKMA, at the MSC-FKMA extra expense of the temporal processing at each stage. 15

4. Non-Cancellation Multistage Source Separation Algorithms u NCMS-FKMA Constrained Criterion: Constraint where (unconstrained optimization problem) Unconstrained Criterion: : projection matrix Theorem 1: Let be the set of all the extracted source signals up to stage. With (A 1), (A 2), and the noise-free assumption, the optimum where is an unknown nonzero constant and. 16
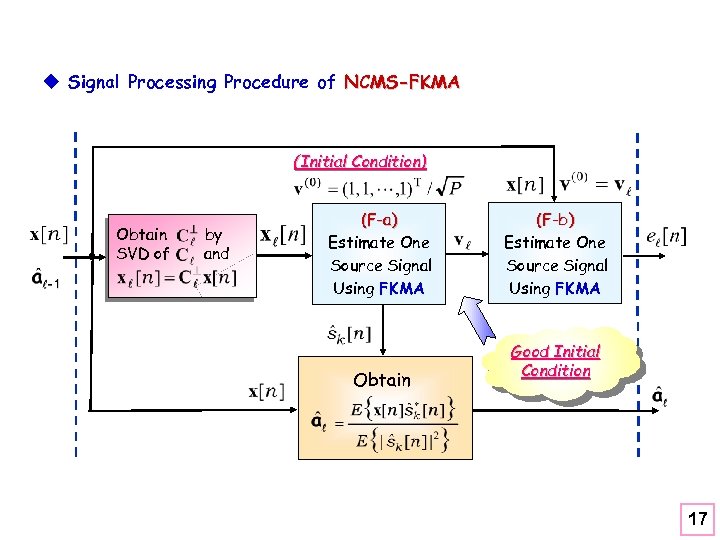
u Signal Processing Procedure of NCMS-FKMA (Initial Condition) Obtain SVD of by and (F-a) Estimate One Source Signal Using FKMA Obtain (F-b) Estimate One Source Signal Using FKMA Good Initial Condition 17

Remarks: l The constrained source extraction filter obtained in (F-a) provides a suitable initial condition for the unconstrained source extraction filter in (F-b), which accordingly leads to one distinct source estimate obtained at each stage neither involving cancellation nor imposing any constraints on the source extraction filter, as well as faster convergence than (F-a). Therefore, unlike the MSC-FKMA, the NCMS-FKMA is free from the error propagation effects at each stage. l As the MSC-TSEA performs better than the MSC-FKMA, the MSC-FKMA NCMS-TSEA also performs better than the NCMS-FKMA at the moderate expense of extra computational load for the temporal processing of the TSEA. 18
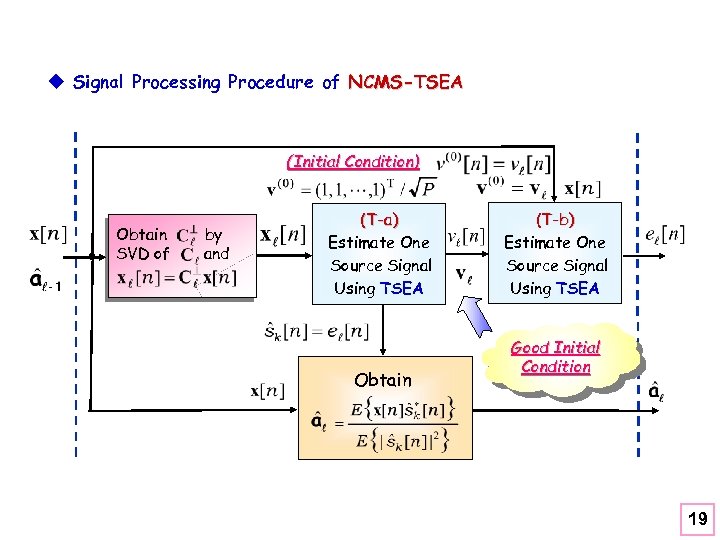
u Signal Processing Procedure of NCMS-TSEA (Initial Condition) Obtain SVD of by and (T-a) Estimate One Source Signal Using TSEA Obtain (T-b) Estimate One Source Signal Using TSEA Good Initial Condition 19

5. Simulation Results --- Part 1 u Parameters Used: l : zero-mean, independent binary sequence of l : generated by filtering l with equal probability : real white Gaussian noise vector through the chosen FIR filters l SNR: l 50 independent runs l Output (extracted) signal to interference-plus-noise ratio (Output SINR) 20

¿ Part A: Performance of NCMS-FKMA and NCMS-TSEA l mixing matrix (taken from Chang et al. , 1998 [9]) (P=5, K=4) l Four cases are considered as follows: Case 1: Output SINR versus SNR for different data length Case 2: Output SINR versus different data length Case 3: Output SINR versus (or . . ) for all. Case 4: (a) Output SINR versus L. (b) versus L. 21
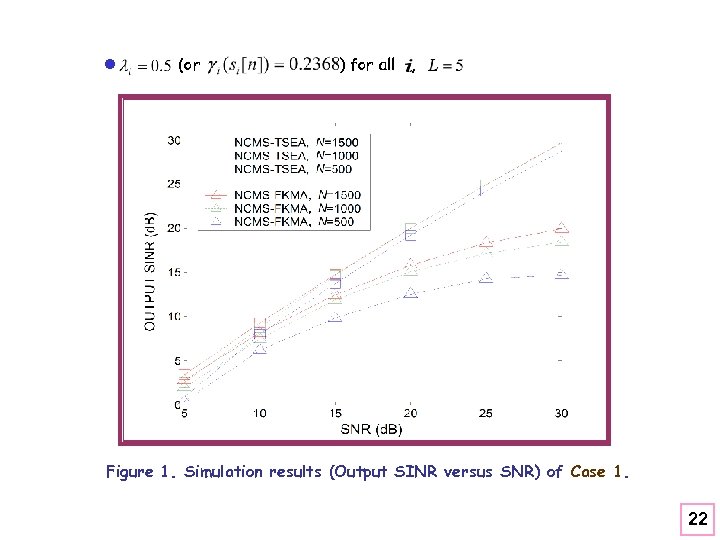
l (or ) for all , Figure 1. Simulation results (Output SINR versus SNR) of Case 1. 22
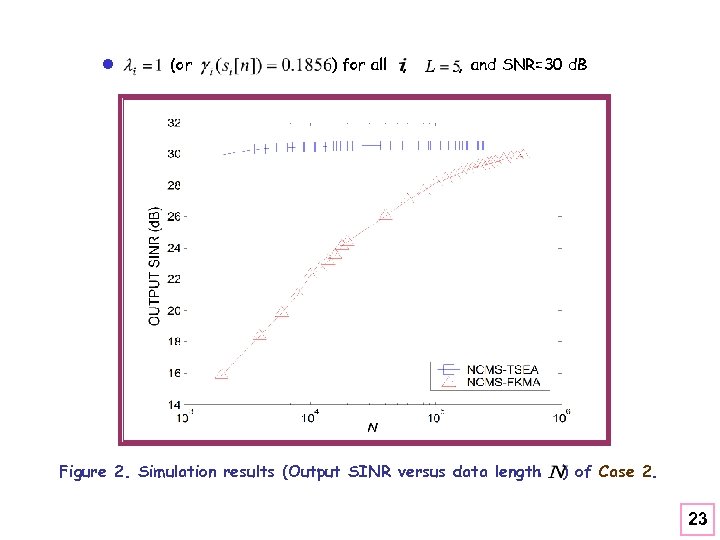
l (or ) for all , , and SNR=30 d. B Figure 2. Simulation results (Output SINR versus data length ) of Case 2. 23
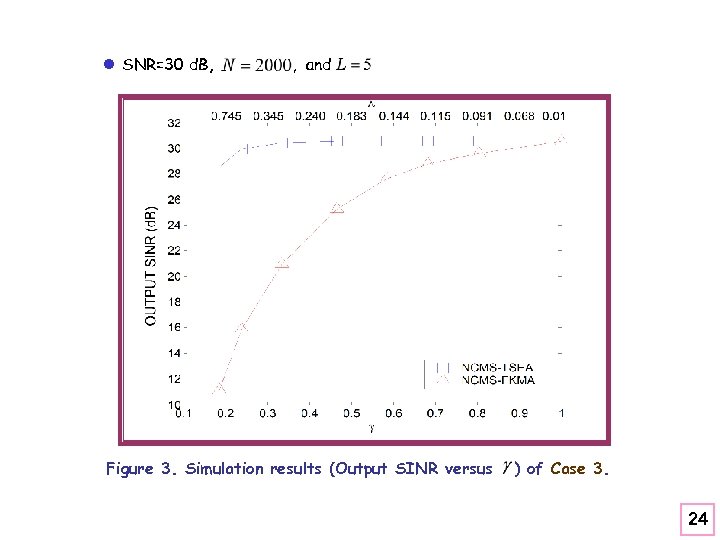
l SNR=30 d. B, , and Figure 3. Simulation results (Output SINR versus ) of Case 3. 24
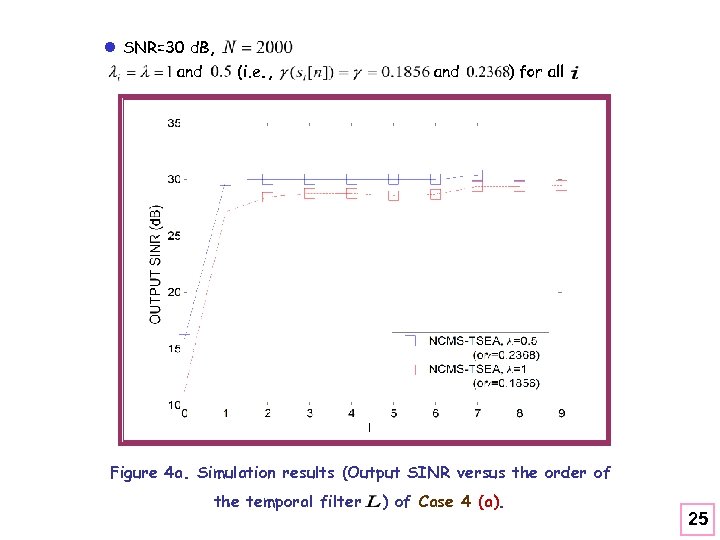
l SNR=30 d. B, and (i. e. , and ) for all Figure 4 a. Simulation results (Output SINR versus the order of the temporal filter ) of Case 4 (a). 25
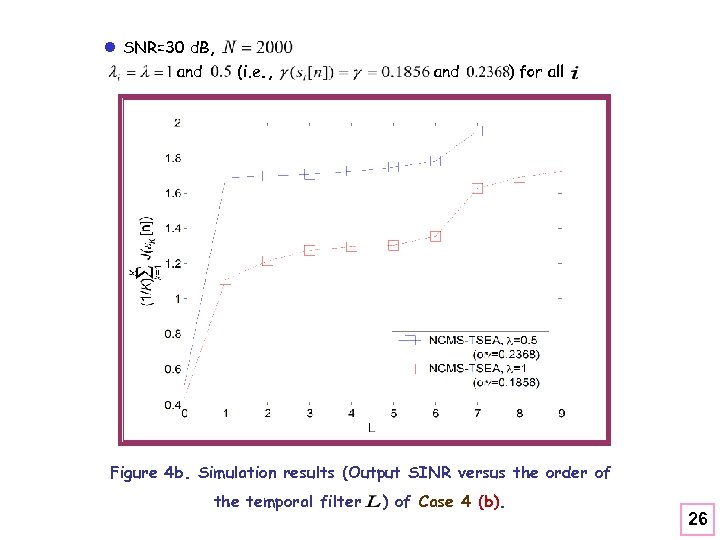
l SNR=30 d. B, and (i. e. , and ) for all Figure 4 b. Simulation results (Output SINR versus the order of the temporal filter ) of Case 4 (b). 26

¿ Part B: Performance Comparison l The same mixing matrix l Data length = 2000 and in Part A and =5 l Comparison with the MSC-FKMA, AMUSE SOBI algorithm (Tong et al. 1990 [1]) and (Belouchrani et al. 1997 [2]) l Three cases are considered as follows: Case A: Output SINR 1 versus SNR for Case B: Output SINR versus SNR for Case C: Output SINR versus and for SNR = 20 d. B and . . 27
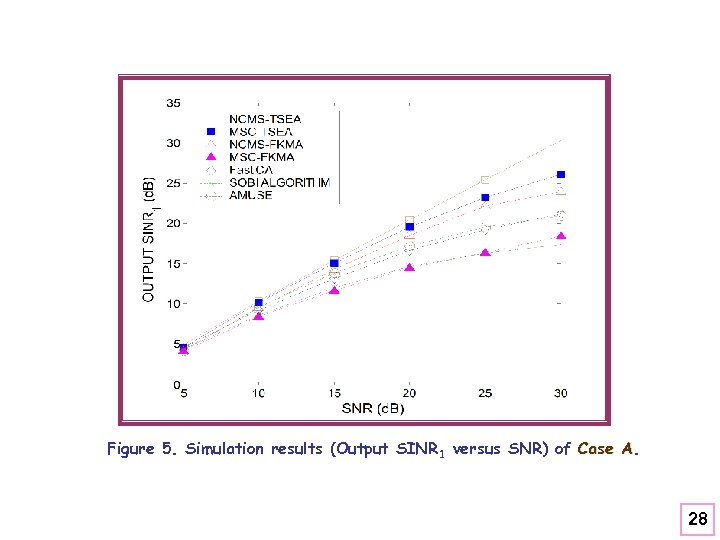
Figure 5. Simulation results (Output SINR 1 versus SNR) of Case A. A 28
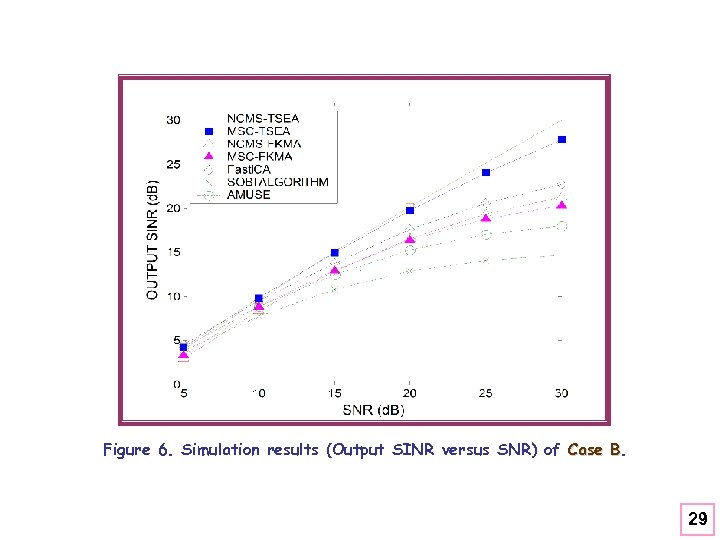
Figure 6. Simulation results (Output SINR versus SNR) of Case B. B 29
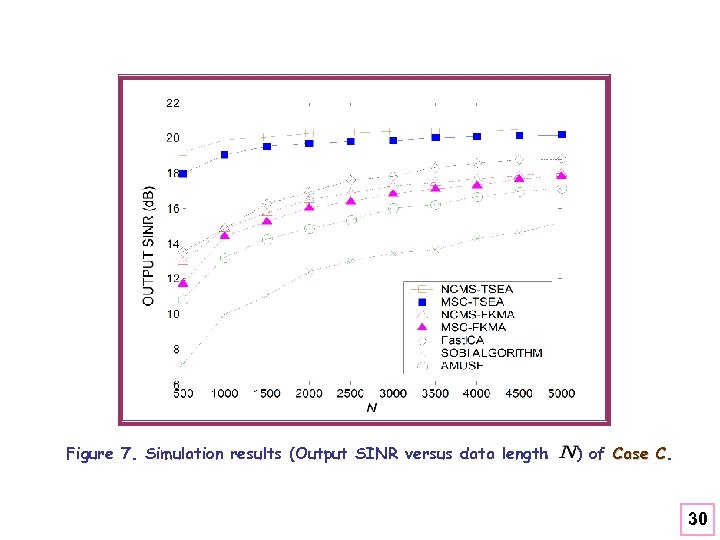
Figure 7. Simulation results (Output SINR versus data length ) of Case C. C 30

Case D: Output SINR versus l : a 3 x 2 mixing matrix by removing the last two rows and columns of the mixing matrix in Part A. (P=3, K=2) Data length =1000, SNR=30 d. B and =3. Comparison with the MSC-FKMA, AMUSE and SOBI algorithm 31
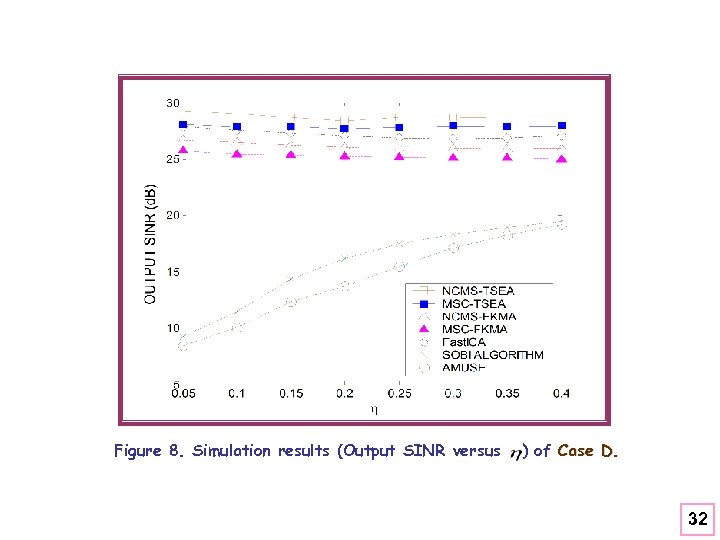
Figure 8. Simulation results (Output SINR versus ) of Case D. 32
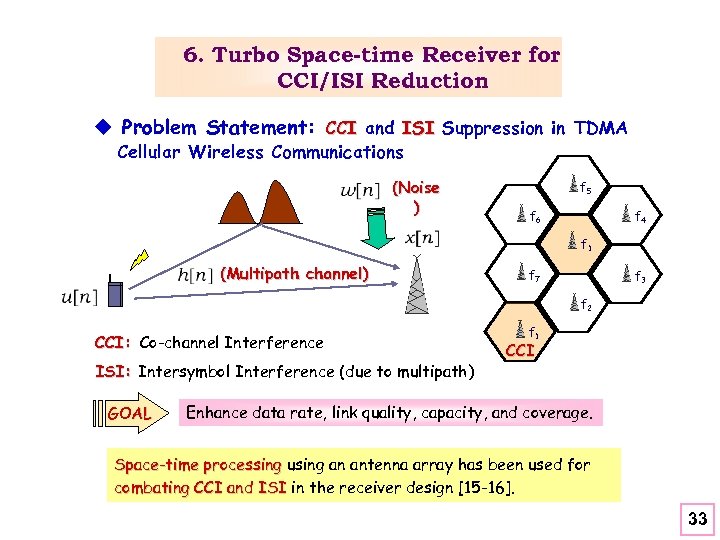
6. Turbo Space-time Receiver for CCI/ISI Reduction u Problem Statement: CCI and ISI Suppression in TDMA Cellular Wireless Communications (Noise ) f 5 f 6 f 4 f 1 (Multipath channel) f 7 f 3 f 2 CCI: Co-channel Interference ISI: Intersymbol Interference (due to multipath) GOAL f 1 CCI Enhance data rate, link quality, capacity, and coverage. Space-time processing using an antenna array has been used for combating CCI and ISI in the receiver design [15 -16]. 33
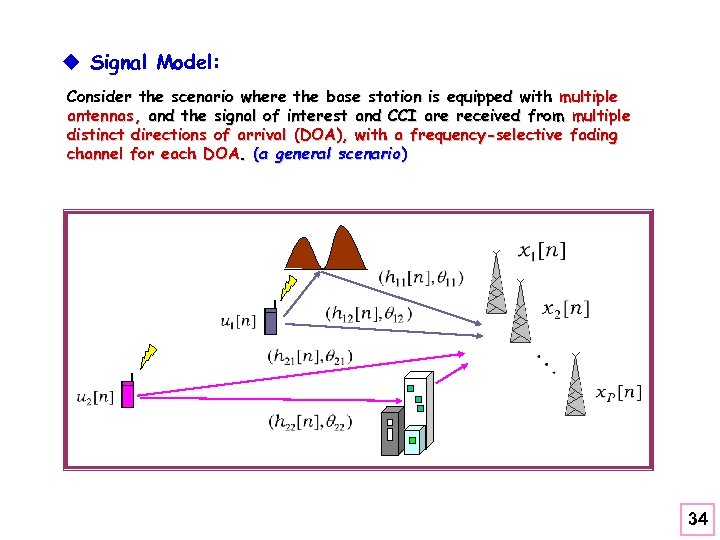
u Signal Model: Consider the scenario where the base station is equipped with multiple antennas, and the signal of interest and CCI are received from multiple distinct directions of arrival (DOA), with a frequency-selective fading channel for each DOA. (a general scenario) 34

The received signal from the desired user and CCIs (users) can be expressed as an instantaneous mixture of multiple sources where ( is no. of DOAs of user k) “ISI-distorted’’ signal (colored signal) from jth DOA of user k steering vector of jth DOA of user k th-order channel impulse response of jth DOA of user k (total no. of DOAs or ’’sources”) 35

u Assumptions: (A 1) The unknown DOA matrix is of full column rank and (A 2) The data sequence of user 1 (the desired signal) is i. i. d. zero-mean non-Gaussian with , and meanwhile statistically independent of the other ( ) zero-mean i. i. d. data sequences (of CCI). (A 3) is zero-mean Gaussian, and statistically independent of for all . (total no. of DOAs or ’’sources”) correlated colored non-Gaussian sources block mutually independent colored sources 36

l Case I: Each user has a single DOA with multiple paths (Venkataraman et al. , 2003), i. e. , Mutually independent colored sources l Case II: Each user has multiple DOAs with disjoint domains of support of multipath channel impulse responses, i. e. , block mutually independent colored sources; mutually independent random variables for each n 37
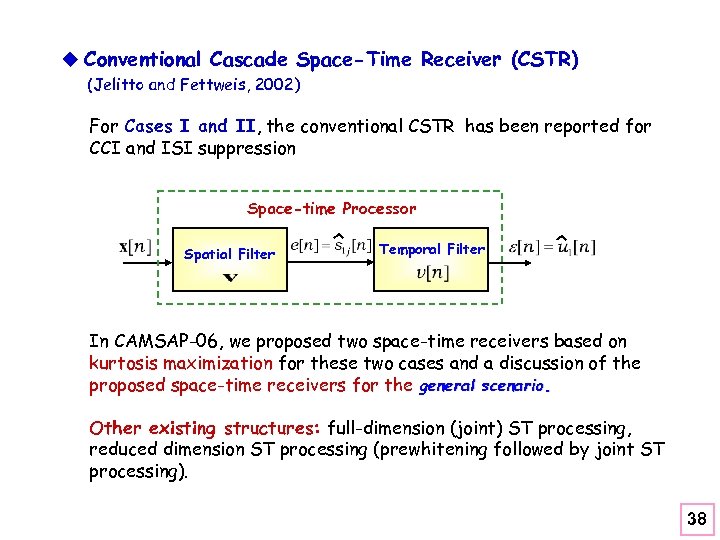
u Conventional Cascade Space-Time Receiver (CSTR) (Jelitto and Fettweis, 2002) For Cases I and II, the conventional CSTR has been reported for CCI and ISI suppression Space-time Processor Spatial Filter Temporal Filter In CAMSAP-06, we proposed two space-time receivers based on kurtosis maximization for these two cases and a discussion of the proposed space-time receivers for the general scenario. Other existing structures: full-dimension (joint) ST processing, reduced dimension ST processing (prewhitening followed by joint ST processing). 38

u Kurtosis Maximization (Ding ad Nguyen, 2000): Maximization magnutude of normalized kutorsis of l Closed-form solution for (noise-free case) is an unknown complex scale factor and : Not existent l Gradient-type iterative algorithms for finding a local optimum Not very computationally efficient : l Applicable not only for Case I but also for Case II (Peng et al. , ICICS 2005) 39
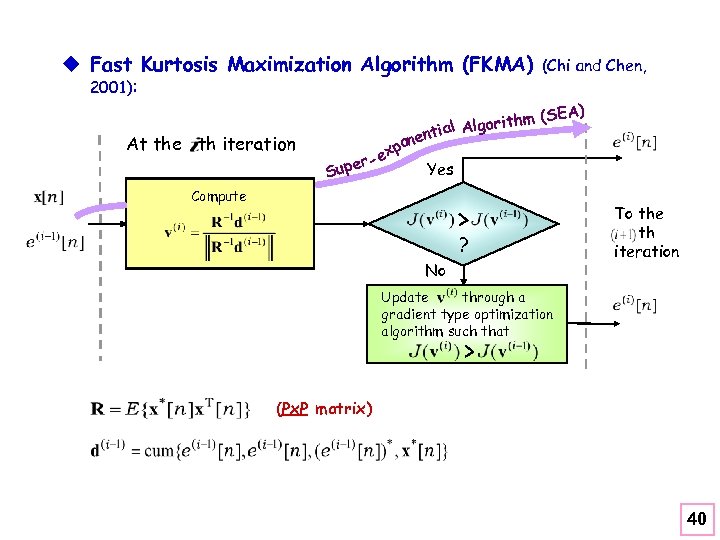
u Fast Kurtosis Maximization Algorithm (FKMA) 2001): At the th iteration (SEA) l Algorithm a enti on p ex er Sup (Chi and Chen, Yes Compute ? No To the th iteration Update through a gradient type optimization algorithm such that (Px. P matrix) 40
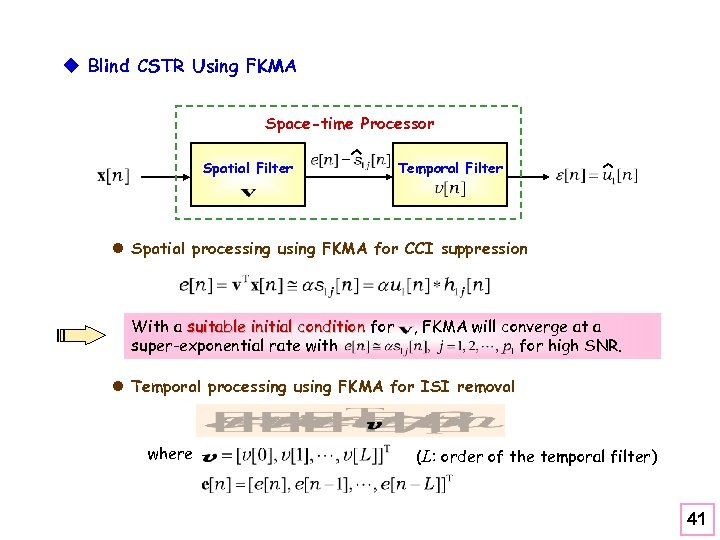
u Blind CSTR Using FKMA Space-time Processor Spatial Filter Temporal Filter l Spatial processing using FKMA for CCI suppression With a suitable initial condition for super-exponential rate with , FKMA will converge at a for high SNR. l Temporal processing using FKMA for ISI removal where (L: order of the temporal filter) 41

l Usually, the ISI-distorted (desired) signal the CCI, (i. e. , , has higher power than all ). So (DOA estimate by delay-and-sum) implying that can be used as the initial condition for the spatial filter needed by the FKMA. l It can be easily shown that (Chi et al. , 2003) where The performance of the spatial filter (to suppress CCI) using FKMA is worse for smaller and worse for larger , leading to limited performance of the temporal filter of the blind CSTR. 42

Blind Turbo Space-Time Receiver (TSTR) u Space-Time Filter for Source Extraction (Chi et al. 2003, 2006): u Design Criterion: Optimum (noise-free case) Maximization 43
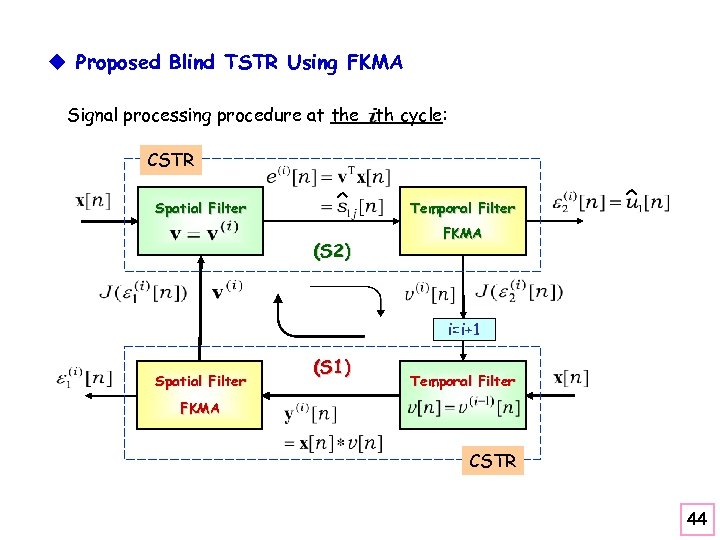
u Proposed Blind TSTR Using FKMA Signal processing procedure at the th cycle: CSTR Spatial Filter Temporal Filter (S 2) FKMA i=i+1 Spatial Filter (S 1) Temporal Filter FKMA CSTR 44

Why? Performance of blind TSTR is superior to blind CSTR. Interpretations: 1) Temporal Processing : Increasing is equivalent to increasing 2) Spatial Processing: 45

Remarks: l It can be proven that for all , implying the guaranteed convergence of the proposed blind TSTR. Typically, the number of cycles spent by the TSTR before convergence, is equal to 2 or 3. The computational load of the blind 3 TSTR is approximately 2 or 3 times that of the blind CSTR. l Because the design of and that of are coupled in a constructive and boosting manner, the proposed blind TSTR outperforms the blind manner CSTR for all , and meanwhile their performance difference is larger for larger. l Compared with the blind CSTR, the proposed blind TSTR is insensitive to the value of (i. e. , robust against channel with multiple paths or severe ISI). 46

Performance of the blind TSTR: where CASE I: CCI suppression by Multiple DOAs suppressed also by CASE II: CCI suppression by GENERAL CASE: CCI suppression by the spatial filter and the temporal filter combine the signals from all the DOAs in a constructive and boosting fashion 47

7. Simulation Results --Part 2 u Scenario of Case I l : zero-mean, independent binary sequence of with equal probability l l , , (array size) : Diagonal matrix : white Gaussian noise vector l SNR: l 50 independent runs 48
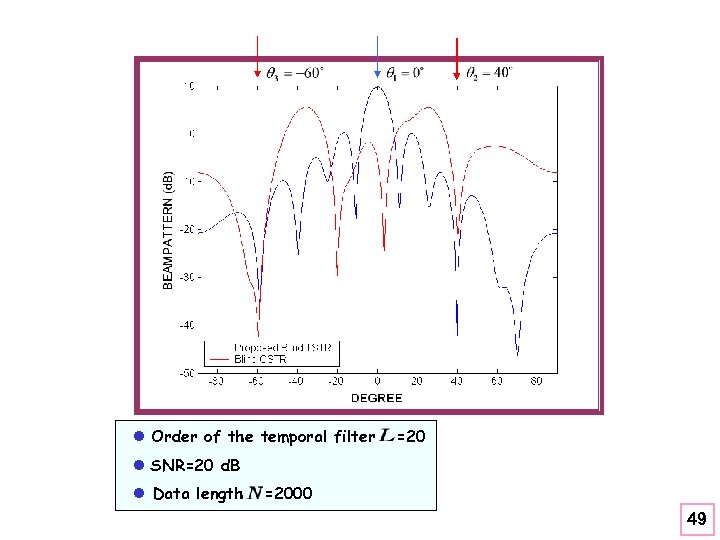
l Order of the temporal filter =20 l SNR=20 d. B l Data length =2000 49
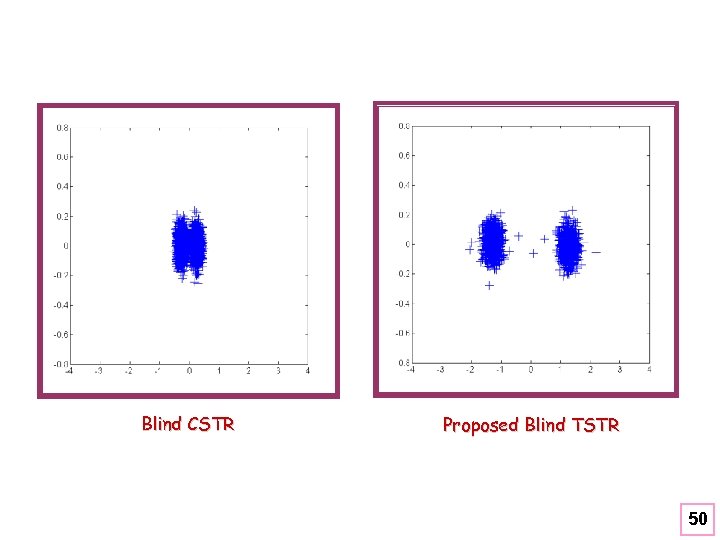
Blind CSTR Proposed Blind TSTR 50
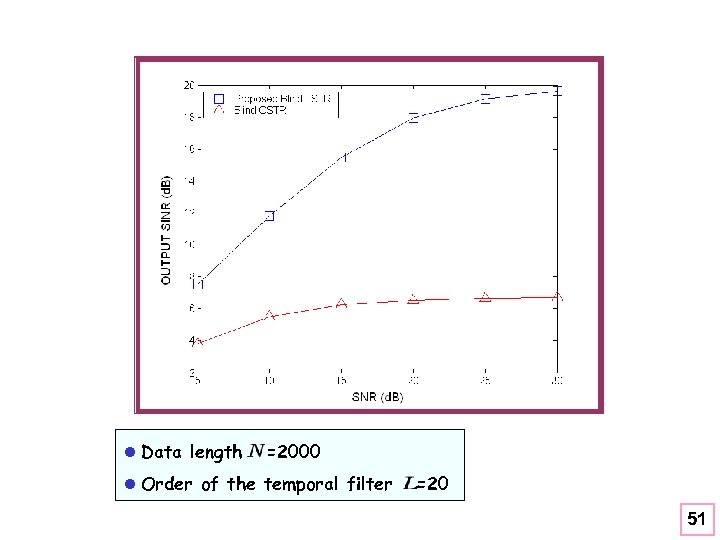
l Data length =2000 l Order of the temporal filter =20 51
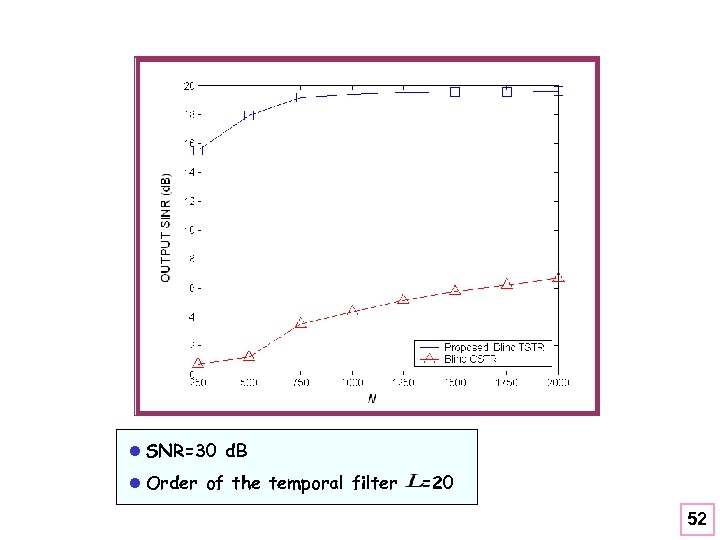
l SNR=30 d. B l Order of the temporal filter =20 52
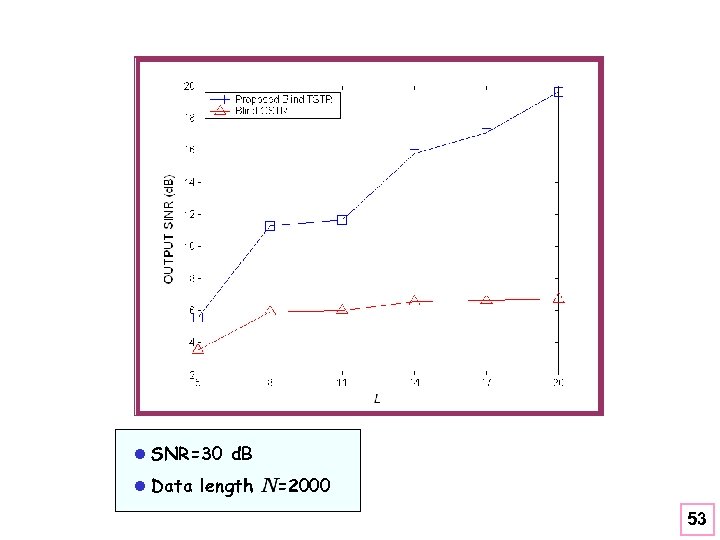
l SNR=30 d. B l Data length =2000 53

u Scenario of Case II l : zero-mean, independent binary sequence of with equal probability l l (array size) : Diagonal matrix : real white Gaussian noise vector l SNR: l 50 independent runs 54
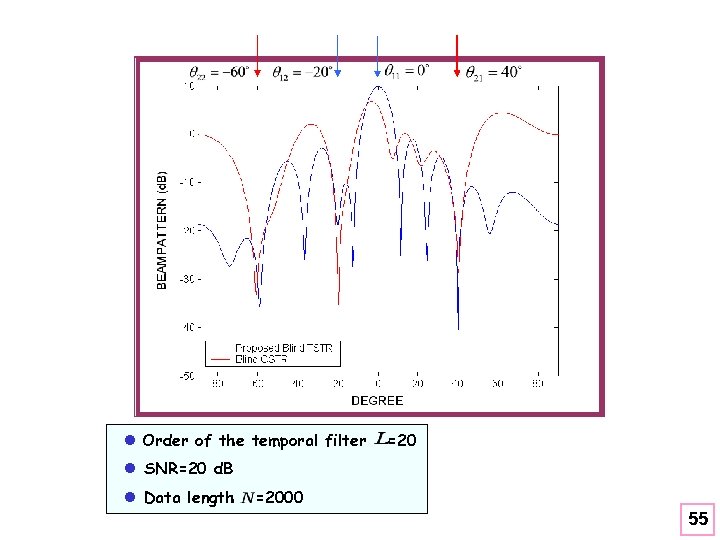
l Order of the temporal filter =20 l SNR=20 d. B l Data length =2000 55
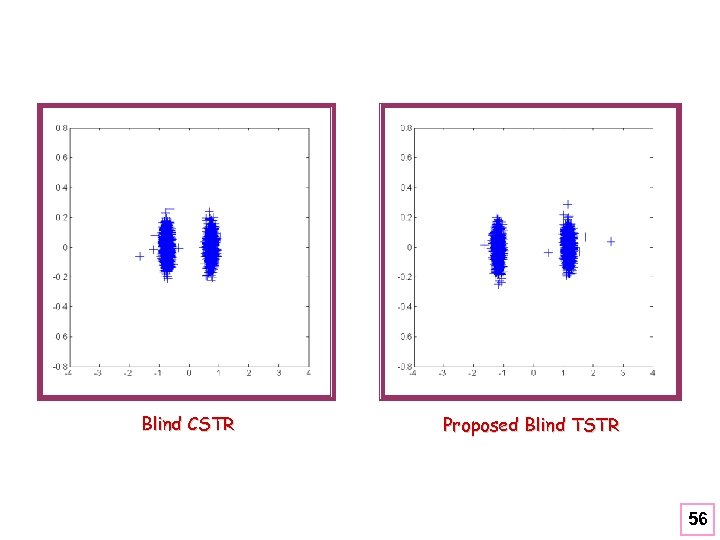
Blind CSTR Proposed Blind TSTR 56
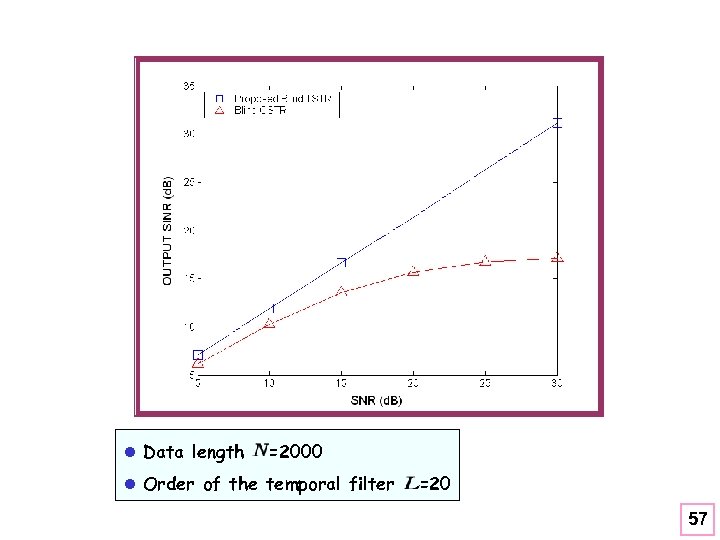
l Data length =2000 l Order of the temporal filter =20 57
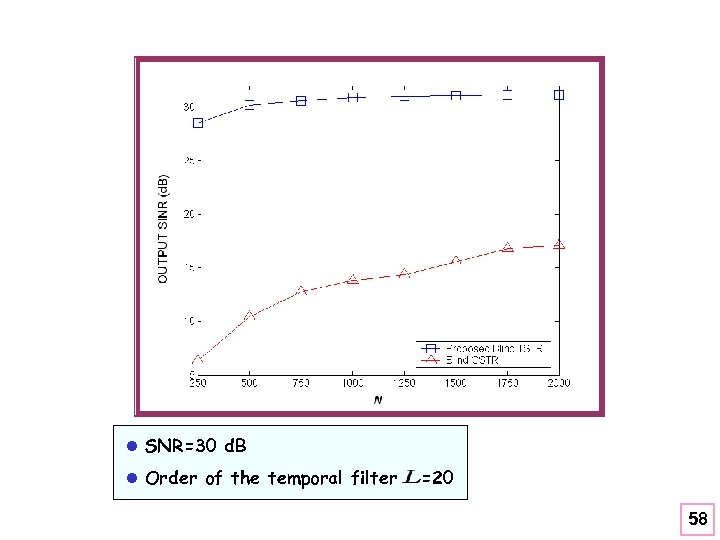
l SNR=30 d. B l Order of the temporal filter =20 58
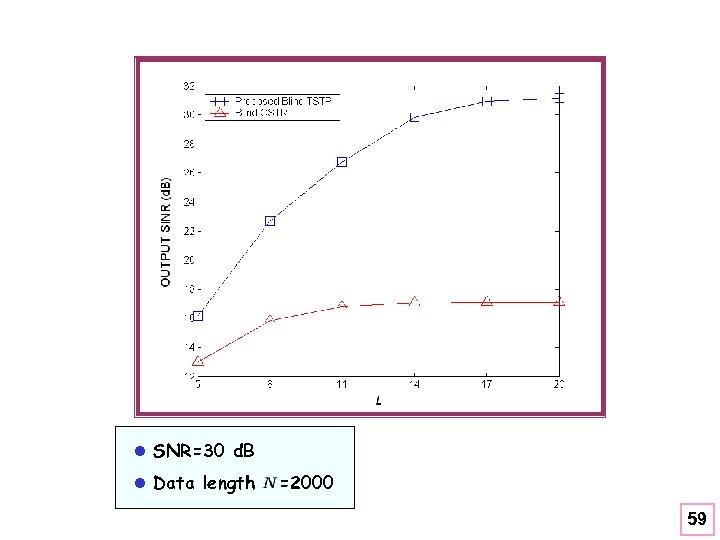
l SNR=30 d. B l Data length =2000 59

u Scenario of the general case l : zero-mean, independent binary sequence of with equal probability l l (array size) : Block-diagonal matrix : white Gaussian noise vector l SNR: l 50 independent runs 60
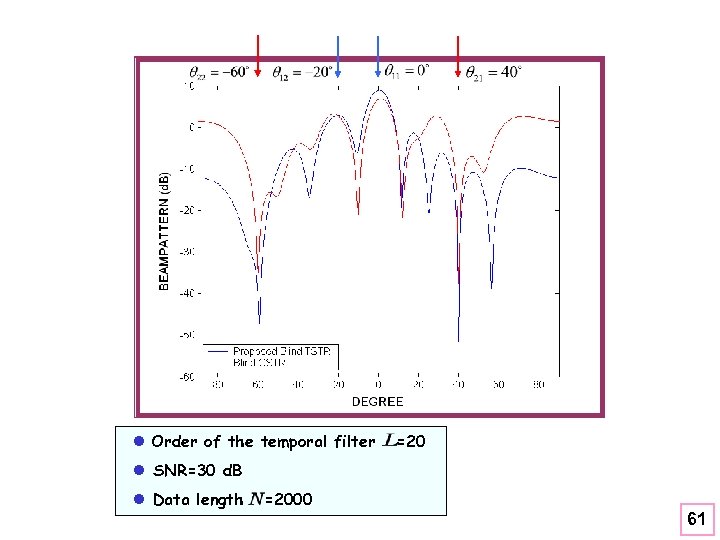
l Order of the temporal filter =20 l SNR=30 d. B l Data length =2000 61
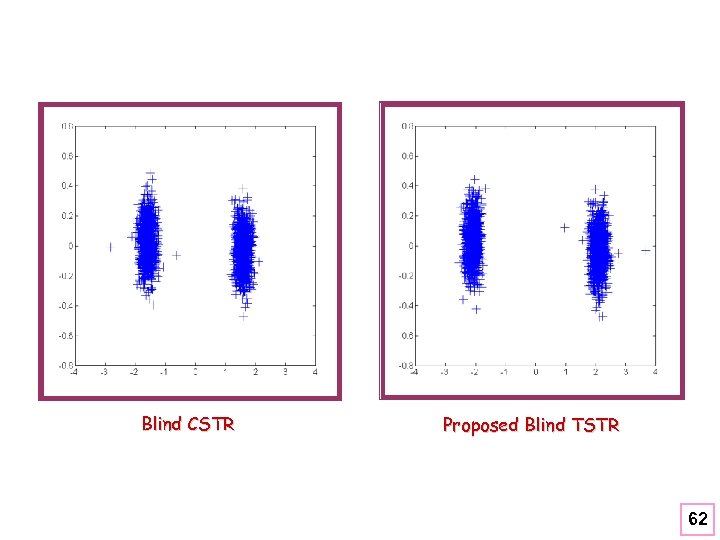
Blind CSTR Proposed Blind TSTR 62
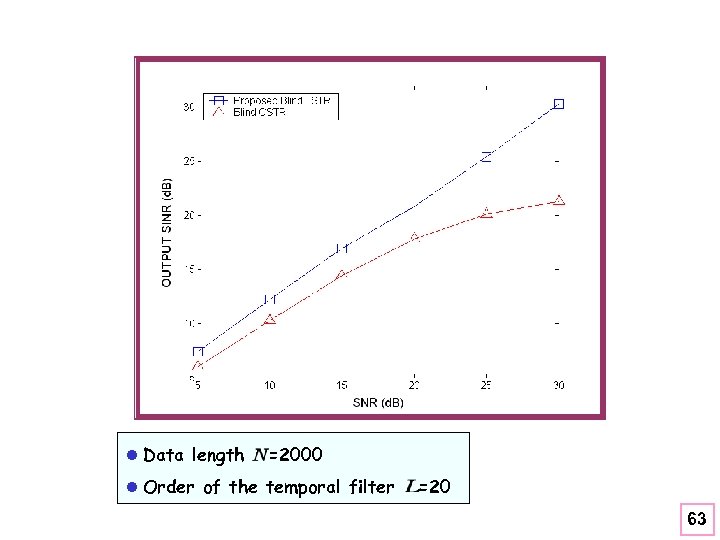
l Data length =2000 l Order of the temporal filter =20 63
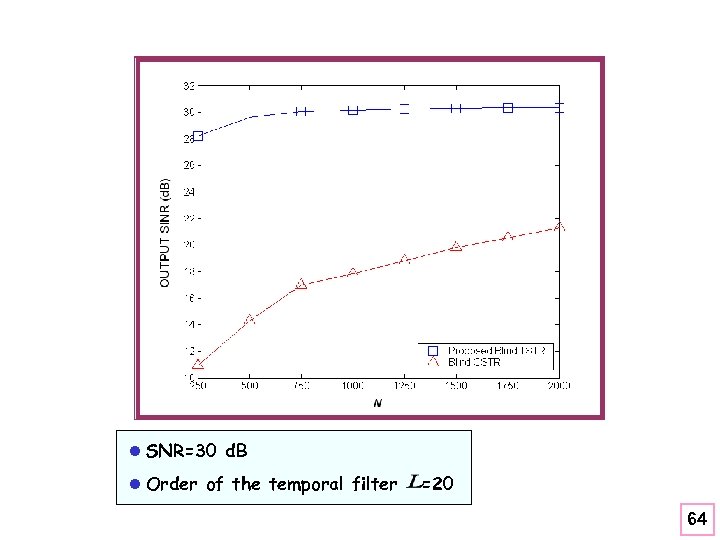
l SNR=30 d. B l Order of the temporal filter =20 64
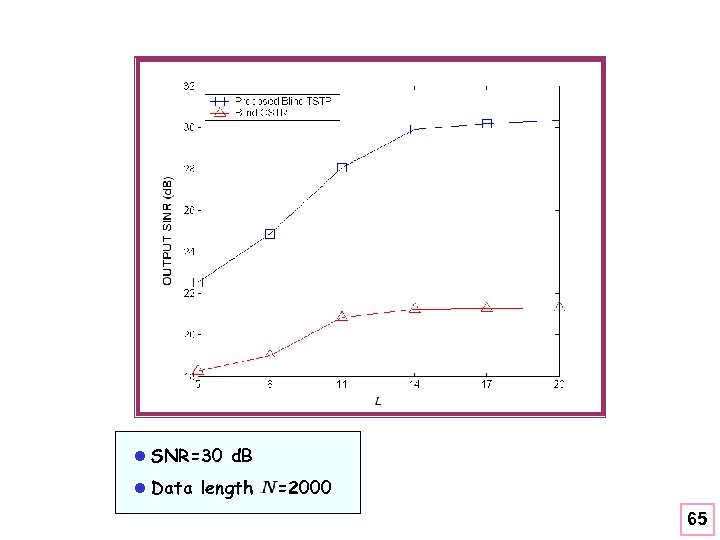
l SNR=30 d. B l Data length =2000 65

8. Conclusions l FKMA only involves spatial processing for extraction of one non-Gaussian (i. i. d. or colored) source from source mixtures. It performs well with super-exponential convergence rate, but its performance depends on the parameter. l We have introduced a novel blind source extraction algorithm, TSEA, which operates cyclically using the FKMA for both of the TSEA temporal processing and spatial processing. The proposed TSEA outperforms the FKMA for in addition to sharing convergence speed and computational efficiency of the later at each cycle. l Because of performance degradation resultant from the error propagation in the MSC procedure, we further introduced two non-cancellation BSS algorithms, namely, NCMS-FKMA and NCMS-TSEA, that can extract a distinct source at each stage without error propagation. 66

l The two BSS algorithms, NCMS-FKMA and NCMS-TSEA perform better than the existing MSC-FKMA and the MSC-TSEA, respectively, with moderately higher computational complexities. l FKMA and TSEA are under investigation for CCI and ISI in MIMO wireless communications (e. g. , OFDM and multi-rate CDMA) and other applications such as 2 -D MIMO systems in biomedical signal processing (with certain constraints or partial correlation between source signals). l Some works of Part 1/Part 2 will be published in C. -Y. Chi and C. -H. Peng, “Turbo source extraction algorithm and noncancellation source separation algorithms by kurtosis maximization, ” IEEE Trans. Signal Processing, vol. 54, no. 8, pp. 2929 -2942, Aug. 2006. C. -H. Peng, C. -Y. Chi and C. -W. Chang, “Blind multiuser detection by kurtosis maximization for asynchronous multi-rate DS/CDMA systems, ” EURASIP Journal on Applied Signal Processing, vol. 2006, Article ID 84930, 17 pages, 2006. doi: 10. 1155/ASP/2006/84930. (special issue: Multisenor Processing for Signal Extraction and Applications) 67

l Background materials of the talk can be found in the following book: C. -Y. Chi, C. -C. Feng, C. -H. Chen and C. -Y. Chen, Blind Equalization and System Identification, London: Springer-Verlag, 2006. Identification Thank you very much 68
![References [1] L. Tong, R. -W. Liu, V. C. Soon, and Y. -F. Huang, References [1] L. Tong, R. -W. Liu, V. C. Soon, and Y. -F. Huang,](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-71.jpg)
References [1] L. Tong, R. -W. Liu, V. C. Soon, and Y. -F. Huang, ``Indeterminacy and identifiability of blind identification, '' IEEE Trans. Circuits and Systems, vol. 38, pp. 499 -509, May 1991. [2] A. Belouchrani, K. Abed-Meraim, J. -F. Cardoso, and E. Moulines, ``A blind source separation technique using second-order statistics, '' IEEE Trans. Signal Processing, vol. 45, pp. 434 -444, Feb. 1997. [3] C. –Y. Chi, C. -J. Chen, F. -Y. Wang, C. -Y. Chen and C. -H. Peng, ``Turbo source separation algorithm using HOS based inverse filter criteria, '' Proc. IEEE International Symposium on Signal Processing and Information Technology, Darmstadt, Germany, Dec. 14 -17, 2003. [4] C. –Y. Chi and C. -Y. Chen, ``Blind beamforming and maximum ratio combining by kurtosis maximization for source separation in multipath, '' Proc. IEEE Workshop on Signal Processing Advances in Wireless Communications, Taoyuan, Taiwan, Mar. 20 -23, 2001, pp. 243 -246. [5] C. -Y. Chi and C. -Y. Chen , C. -H. Chen and C. -C. Feng, ``Batch processing algorithms for blind equalization using higher-order statistics, '' IEEE Signal Processing Magazine, vol. 20, pp. 25 -49, Jan. 2003. 69
![[6] J. M. Mendel, ``Tutorial on higher-order statistic (spectra) in signal processing and system [6] J. M. Mendel, ``Tutorial on higher-order statistic (spectra) in signal processing and system](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-72.jpg)
[6] J. M. Mendel, ``Tutorial on higher-order statistic (spectra) in signal processing and system theory: theoretical results and some applications, '' Proc. IEEE, vol. 79, pp. 278 -305, Mar. 1991. [7] C. -Y. Chi, C. -H. Chen and C. -Y. Chen, ``Blind MAI and ISI suppression for DS/CDMA systems using HOS-based inverse filter criteria, '' IEEE Trans. Signal Processing, vol. 50, pp. 1368 -1381, June 2002. [8] Z. Ding and T. Nguyen, ``Stationary points of a kurtosis maximization algorithm for blind signal separation and antenna beamforming, '' IEEE Trans. Signal Processing, vol. 48, pp. 1587 -1596, June 2000. [9] C. Chang, Z. Ding, S. F. Yau, and F. H. Y. Chan, ``A matrix-pencil approach to blind separation of non-white sources in white noise, '' Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing, Seattle, WA, May 12 -15, 1998, pp. 2485 -2488. [10] D. J. Moelker, A. Shah and Y. Bar-Ness, ``The generalized maximum SINR array processor for personal communication systems in a multipath environment, '' Proc. IEEE International Symposium on Personal, Indoor, and Mobil Radio Communications, vol. 2, Taipei, Oct. 15 -18, 1996, pp. 531 -534. [11] V. Venkataraman, R. E. Cagley and J. J. Shynk, ``Adaptive beamforming for interference rejection in an OFDM system, '' IEEE Conference Record of the Thirty-Seventh Asilomar Conference on SSC, Nov. 9 -12, 2003, vol. 1, pp. 507 -511. 70
![[12] J. -F. Cardoso, ``Source separation using higher order moments, '' Proc. IEEE International [12] J. -F. Cardoso, ``Source separation using higher order moments, '' Proc. IEEE International](https://present5.com/presentation/eaf0e194b06aaa0da0483b08bffa3863/image-73.jpg)
[12] J. -F. Cardoso, ``Source separation using higher order moments, '' Proc. IEEE International Conference on Acoustics, Speech, and Signal Processing, Glasgow, UK, May 23 -26, 1989, pp. 2109 -2112. [13] A. Hyvärinen, J. Karhunen, and E. Oja, Independent Component Analysis. New York: Wiley. Interscience, 2001. [14] A. Hyvärinen and E. Oja, ``A fixed-point algorithm for independent component analysis, '' Neural Computation, vol. 9, pp. 1482 -1492, 1997. [15] J. Jelitto and G. Fettweis, ``Reduced dimension space-time processing for multi-antenna wireless systems, '' IEEE Wireless Communications Mag. , vol. 9, pp. 18 -25, Dec. 2002. [16] Jen-Wei Liang and A. J. Paulraj, ``Two stage CCI/ISI reduction with space-time processing in TDMA cellular networks, '' Proc. 30 th Asilomar Conference on Signals, Systems, and Computers, vol. 1, Pacific Grove, CA, Nov. 3 -6, 1996, pp. 607 -611. 71
eaf0e194b06aaa0da0483b08bffa3863.ppt