Blackbodies and Lasers Prof Rick Trebino Georgia Tech

Blackbodies and Lasers* Prof. Rick Trebino, Georgia Tech www. frog. gatech. edu Boltzmann’s Law Stimulated Emission Gain Inversion The Laser Four-level System Threshold Some lasers * Light Amplification by Stimulated Emission of Radiation

Calculations in Physics: Semi-Classical physics The least precise calculations are performed completely classically and using Newton’s Laws. The most precise computations are performed fully quantummechanically, using the precise potential, solving Schrodinger’s Equation for it, and including superpositions of states, when appropriate. But they are usually very difficult—or impossible. Intermediate cases involve semi-classical computations, in which an atom’s energy levels are computed quantum-mechanically, but superpositions are neglected. Light waves may be treated classically or as photons. We’ll now do two semi-classical calculations, one of the blackbody radiation spectrum and another of laser threshold, in which we’ll treat molecules as energy levels and light as photons.

Another Big Simplification: The Two-Level System All atoms and molecules have infinitely many states and their corresponding energy levels. That’s also too complicated. This doesn’t always work. Excited level Energy So, if a photon whose energy matches a particular transition energy is present, physicists usually just consider two states and their corresponding energy levels. Ground level

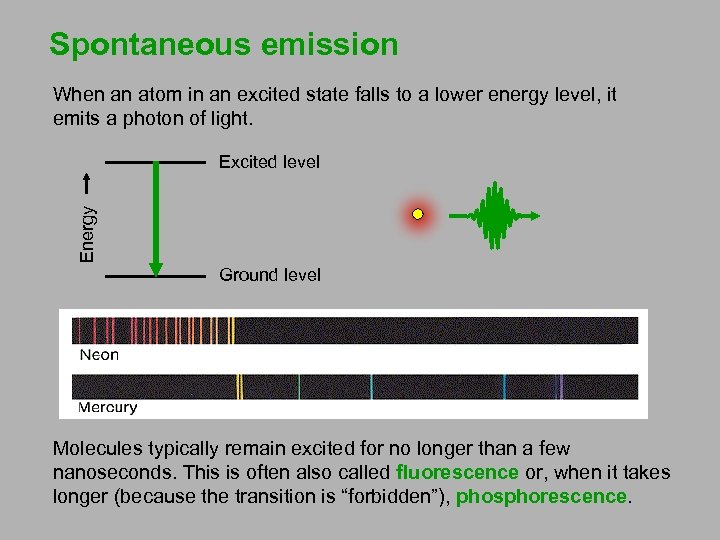
Spontaneous emission When an atom in an excited state falls to a lower energy level, it emits a photon of light. Energy Excited level Ground level Molecules typically remain excited for no longer than a few nanoseconds. This is often also called fluorescence or, when it takes longer (because the transition is “forbidden”), phosphorescence.

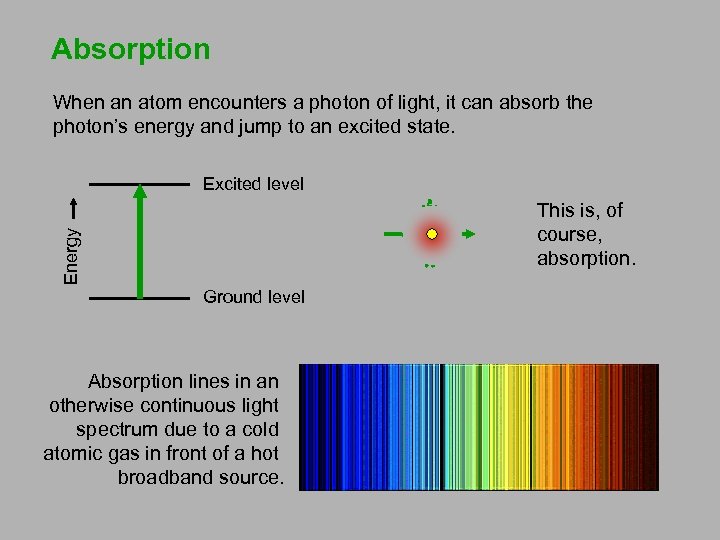
Absorption When an atom encounters a photon of light, it can absorb the photon’s energy and jump to an excited state. Excited level Energy This is, of course, absorption. Ground level Absorption lines in an otherwise continuous light spectrum due to a cold atomic gas in front of a hot broadband source.

Einstein showed that another process, stimulated emission, can also occur. When a photon encounters an atom in an excited state, the photon can induce the atom to emit its energy as another photon of light, resulting in two identical photons. Energy Excited level Ground level Einstein first proposed stimulated emission in 1916.

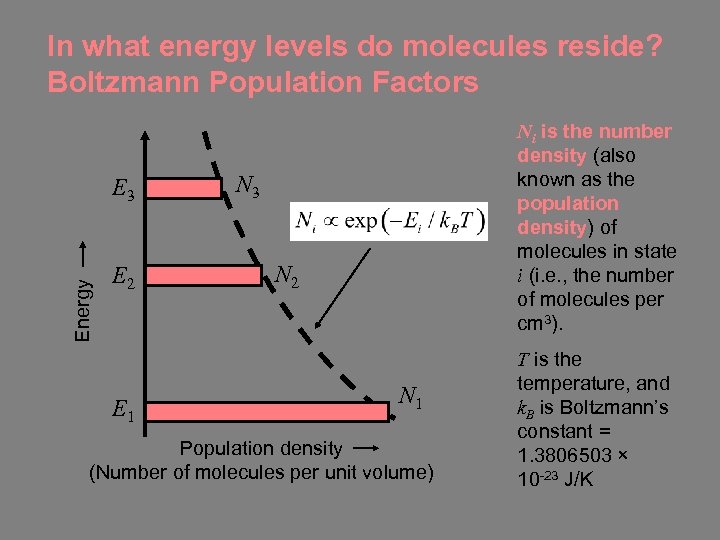
In what energy levels do molecules reside? Boltzmann Population Factors Energy E 3 E 2 E 1 Ni is the number density (also known as the population density) of molecules in state i (i. e. , the number of molecules per cm 3). N 3 N 2 N 1 Population density (Number of molecules per unit volume) T is the temperature, and k. B is Boltzmann’s constant = 1. 3806503 × 10 -23 J/K

The Maxwell-Boltzman Distribution In the absence of collisions, molecules tend to remain in the lowest energy state available. Collisions can knock a molecule into a higher-energy state. The higher the temperature, the more this happens. High T Energy Low T 3 2 1 1 Molecules In equilibrium, the ratio of the populations of two states is: N 2 / N 1 = exp(-DE/k. BT), where DE = E 2 – E 1 = hn As a result, higher-energy states are always less populated than the ground state, and absorption is stronger than stimulated emission.

Blackbody Radiation Blackbody radiation is emitted from a hot body. It's anything but black! The name comes from the assumption that the body absorbs at every frequency and hence would look black at low temperature. It results from a combination of spontaneous emission, stimulated emission, and absorption occurring in a medium at a given temperature. It assumes that the box is filled with many different molecules that, together, have transitions (absorptions) at every wavelength.

Einstein A and B Coefficients In 1916, Einstein considered the various transition rates between molecular states (say, 1 and 2) involving light of intensity, I: at frequency n Spontaneous emission rate = A N 2 Absorption rate = B 12 N 1 I Stimulated emission rate = B 21 N 2 I In equilibrium, the rate of upward transitions equals the rate of downward transitions: A N 2 + B 21 N 2 I = Down = Up = B 12 N 1 I Dividing by N 1 (A + B 21 I ) yields N 2/N 1: Recalling the Maxwell. Boltzmann Distribution (B 12 I ) / (A + B 21 I ) = N 2 / N 1 = exp(–DE/k. BT)

Blackbody Radiation Now solve for the intensity in: (B 12 I) / (A + B 21 I) = exp(-DE/k. BT) Multiply by (A + B 21 I) exp(DE/k. BT): B 12 I exp(DE/k. BT) = A + B 21 I Solve for I: I = A / [B 12 exp(DE/k. BT) – B 21] Dividing numerator and denominator by B 21: I = (A/B 21) / [(B 12/B 21) exp(DE/k. BT) – 1] Now, when T ® ¥, I should also. As T ® ¥, exp(DE/k. BT) ® 1. So: And: (B 12/B 21) – 1 = 0 B 12 = B 21 º B ¬ Coeff up = coeff down! I = (A/B) / [exp(DE/k. BT) – 1]

Blackbody Radiation I = (A/B) / [exp(DE/k. BT ) – 1] We can eliminate A/B based on other information and, writing in terms of the intensity per unit frequency, In : also using DE = hn This is the total intensity per unit frequency (that is, in a range from n to n + dn ) emitted by an arbitrary blackbody. We considered only two levels, but our approach was general and so applies to any two levels and hence to the entire spectrum. Notice that it’s independent of the size of the object. To obtain the emitted power, multiply by the surface area of the blackbody.

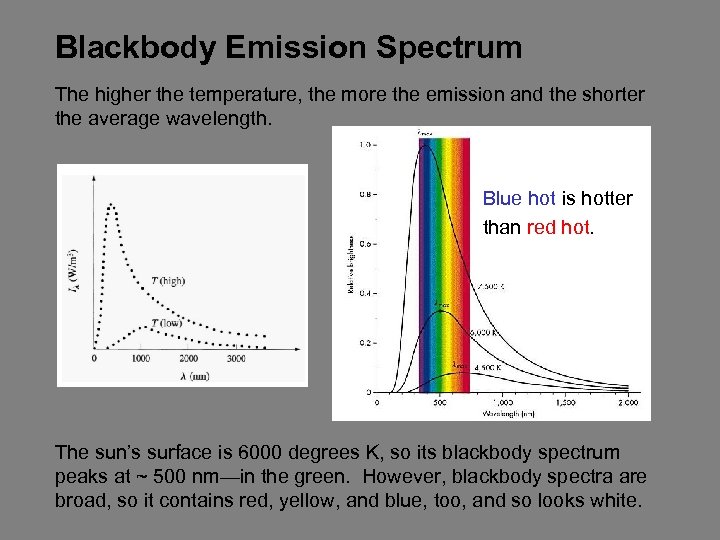
Blackbody Emission Spectrum The higher the temperature, the more the emission and the shorter the average wavelength. Blue hot is hotter than red hot. The sun’s surface is 6000 degrees K, so its blackbody spectrum peaks at ~ 500 nm—in the green. However, blackbody spectra are broad, so it contains red, yellow, and blue, too, and so looks white.

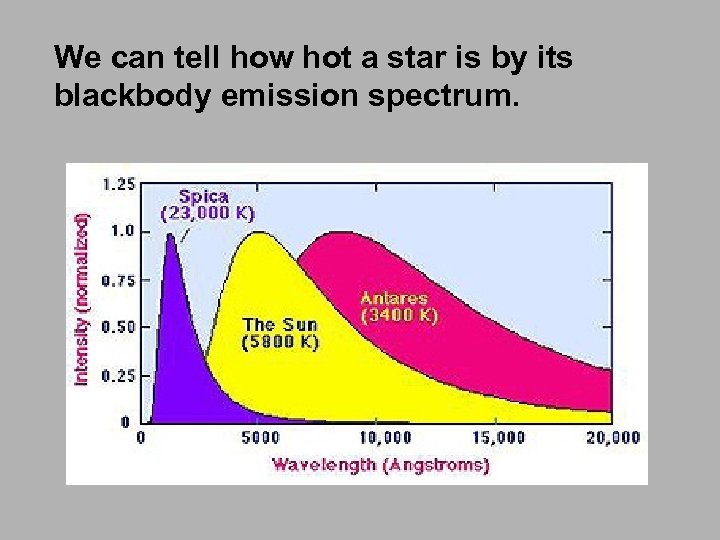
We can tell how hot a star is by its blackbody emission spectrum.

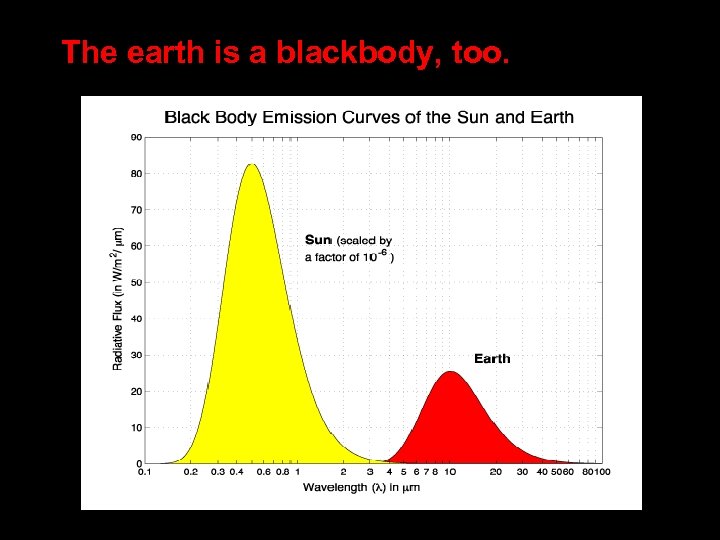
The earth is a blackbody, too.

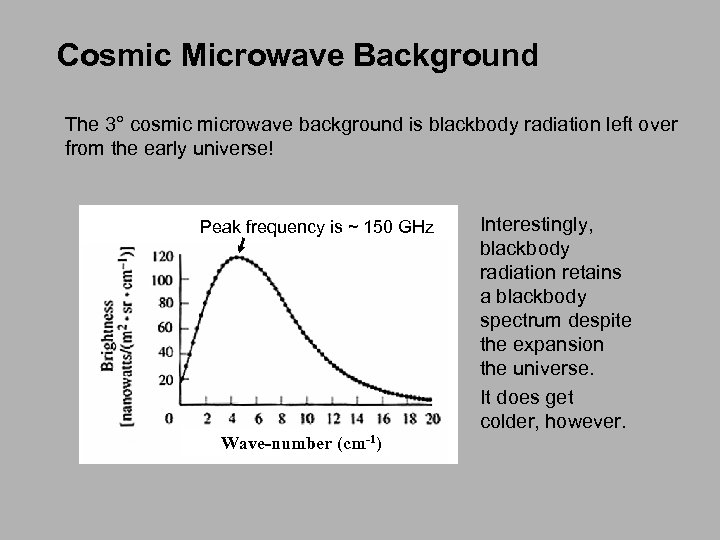
Cosmic Microwave Background The 3° cosmic microwave background is blackbody radiation left over from the early universe! Peak frequency is ~ 150 GHz Wave-number (cm-1) Interestingly, blackbody radiation retains a blackbody spectrum despite the expansion the universe. It does get colder, however.

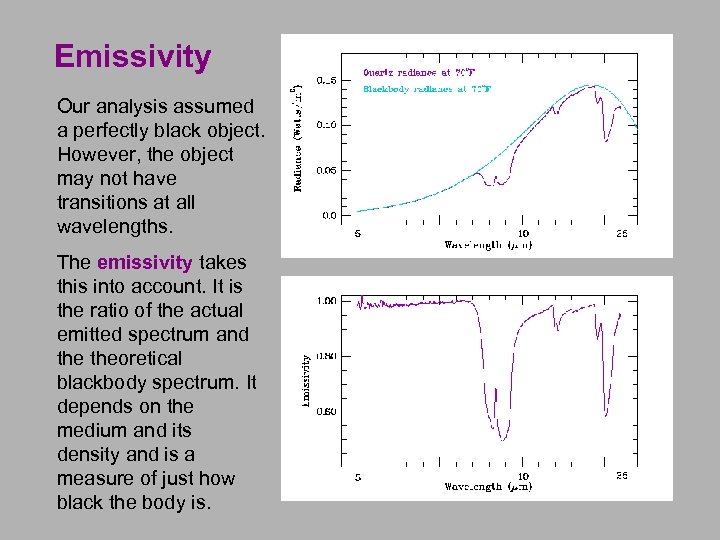
Emissivity Our analysis assumed a perfectly black object. However, the object may not have transitions at all wavelengths. The emissivity takes this into account. It is the ratio of the actual emitted spectrum and theoretical blackbody spectrum. It depends on the medium and its density and is a measure of just how black the body is.

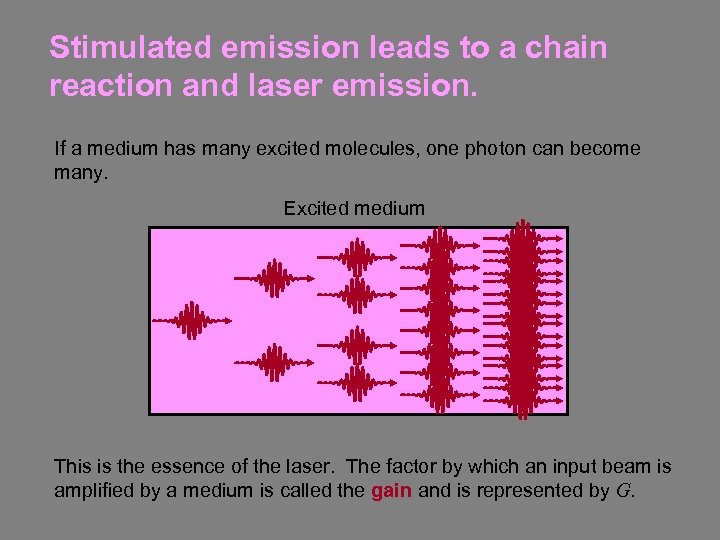
Stimulated emission leads to a chain reaction and laser emission. If a medium has many excited molecules, one photon can become many. Excited medium This is the essence of the laser. The factor by which an input beam is amplified by a medium is called the gain and is represented by G.

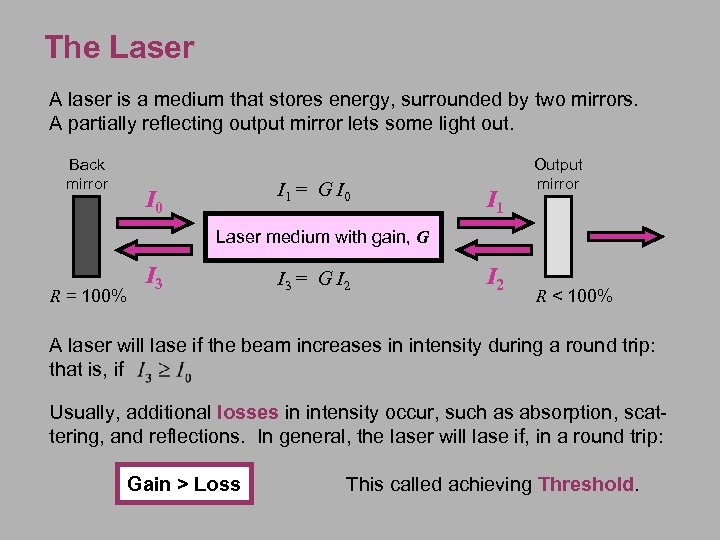
The Laser A laser is a medium that stores energy, surrounded by two mirrors. A partially reflecting output mirror lets some light out. Back mirror I 1 = G I 0 I 1 Output mirror Laser medium with gain, G R = 100% I 3 = G I 2 R < 100% A laser will lase if the beam increases in intensity during a round trip: that is, if Usually, additional losses in intensity occur, such as absorption, scattering, and reflections. In general, the laser will lase if, in a round trip: Gain > Loss This called achieving Threshold.

Inversion In order to achieve G > 1, stimulated emission must exceed absorption: B N 2 I > B N 1 I Inversion N 2 > N 1 This condition is called inversion. It does not occur naturally (it’s forbidden by the Boltzmann distribution). It’s inherently a non-equilibrium state. Energy Or, equivalently, “Negative temperature” Molecules In order to achieve inversion, we must hit the laser medium very hard in some way and choose our medium correctly.

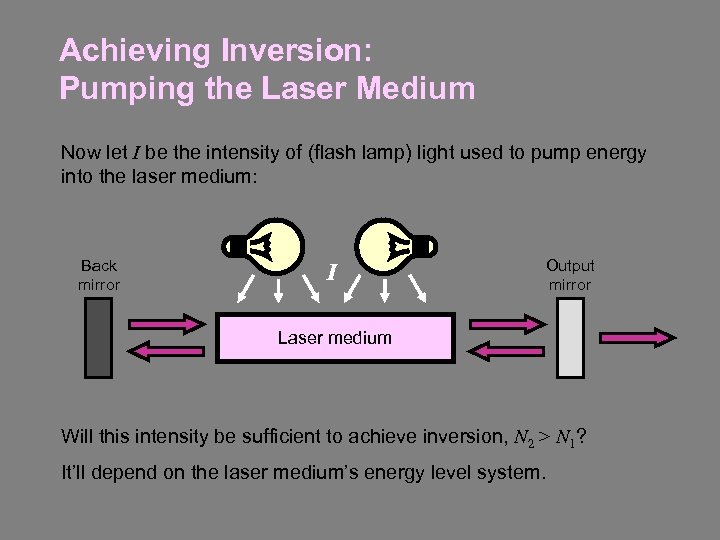
Achieving Inversion: Pumping the Laser Medium Now let I be the intensity of (flash lamp) light used to pump energy into the laser medium: Back mirror I Output mirror Laser medium Will this intensity be sufficient to achieve inversion, N 2 > N 1? It’ll depend on the laser medium’s energy level system.

Rate Equations for a Two-Level System 2 Pump Rate equations for the densities of the two states: Absorption Stimulated emission N 2 Laser 1 N 1 Spontaneous emission Pump intensity If the total number of molecules is N:

Why Inversion is Impossible in a Two-Level System 2 N 2 Laser 1 In steady-state: where: Isat is the saturation intensity. DN is always positive, no matter how high I is! It’s impossible to achieve an inversion in a two-level system! N 1

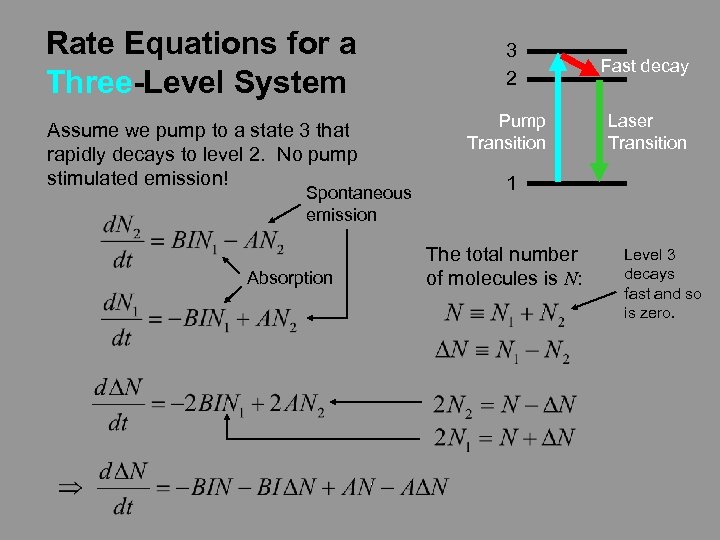
Rate Equations for a Three-Level System Assume we pump to a state 3 that rapidly decays to level 2. No pump stimulated emission! Spontaneous emission Absorption 3 2 Fast decay Pump Transition Laser Transition 1 The total number of molecules is N: Level 3 decays fast and so is zero.

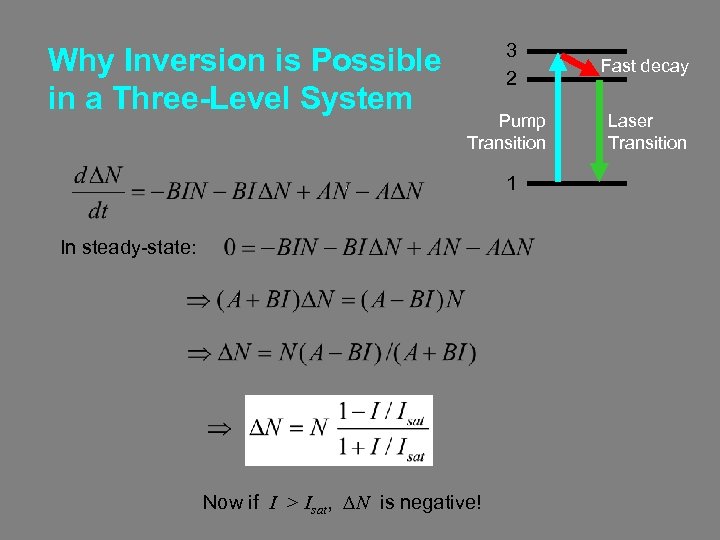
Why Inversion is Possible in a Three-Level System 3 2 Fast decay Pump Transition Laser Transition 1 In steady-state: Now if I > Isat, DN is negative!

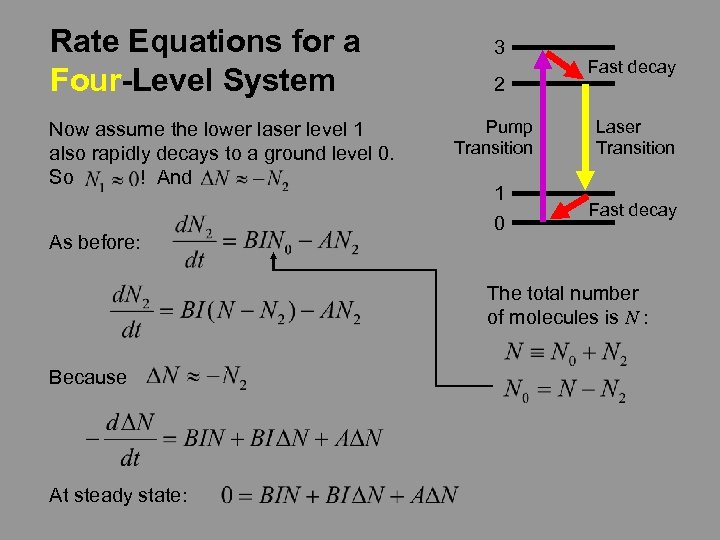
Rate Equations for a Four-Level System Now assume the lower laser level 1 also rapidly decays to a ground level 0. So ! And As before: 3 2 Fast decay Pump Transition Laser Transition 1 0 Fast decay The total number of molecules is N : Because At steady state:

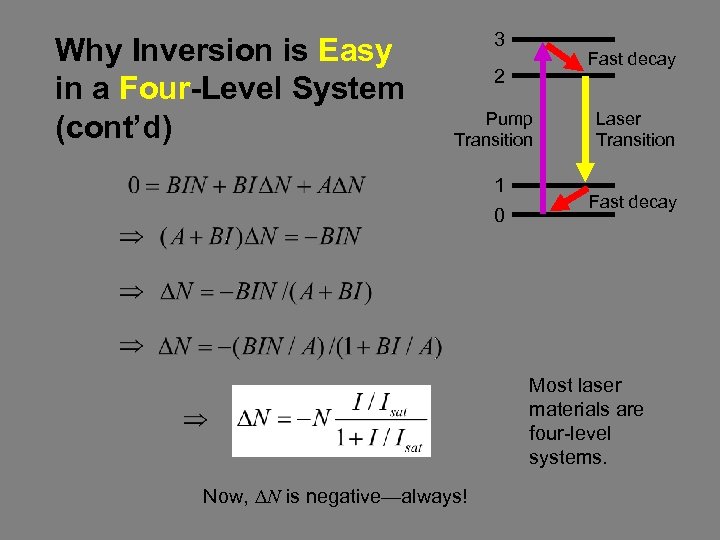
Why Inversion is Easy in a Four-Level System (cont’d) 3 Fast decay 2 Pump Transition Laser Transition 1 0 Fast decay Most laser materials are four-level systems. Now, DN is negative—always!

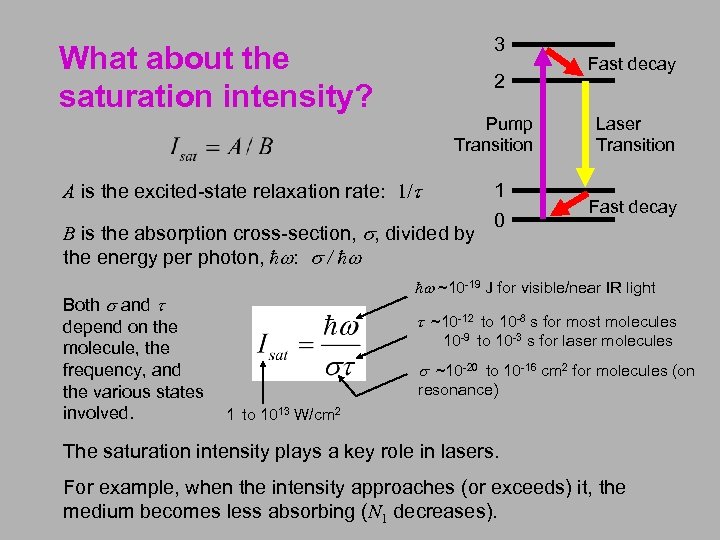
3 What about the saturation intensity? 2 Pump Transition Laser Transition 1 0 Fast decay A is the excited-state relaxation rate: 1/t B is the absorption cross-section, s, divided by the energy per photon, ħw: s / ħw Both s and t depend on the molecule, the frequency, and the various states involved. 1 to 1013 W/cm 2 Fast decay ħw ~10 -19 J for visible/near IR light t ~10 -12 to 10 -8 s for most molecules 10 -9 to 10 -3 s for laser molecules s ~10 -20 to 10 -16 cm 2 for molecules (on resonance) The saturation intensity plays a key role in lasers. For example, when the intensity approaches (or exceeds) it, the medium becomes less absorbing (N 1 decreases).

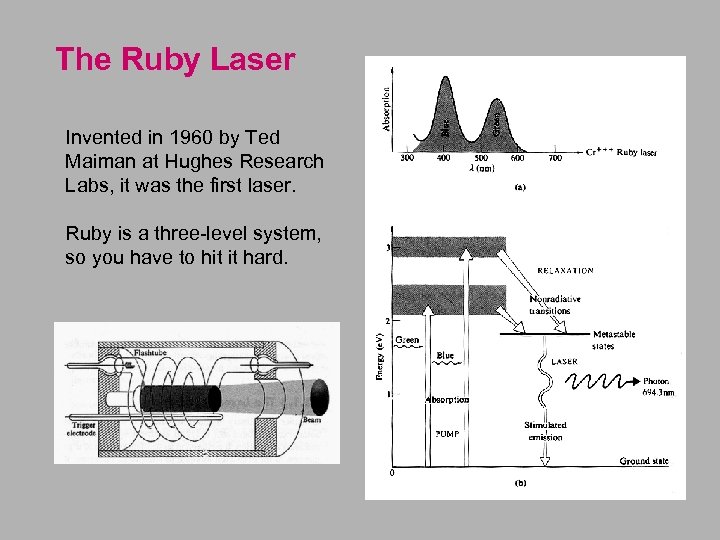
The Ruby Laser Invented in 1960 by Ted Maiman at Hughes Research Labs, it was the first laser. Ruby is a three-level system, so you have to hit it hard.

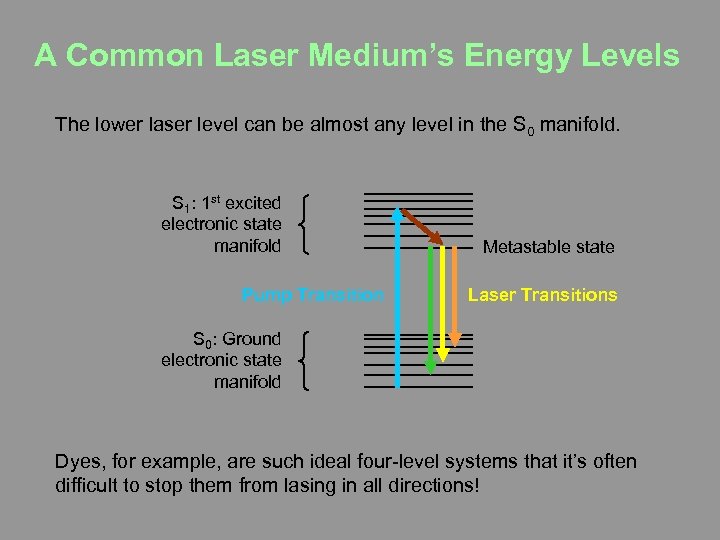
A Common Laser Medium’s Energy Levels The lower laser level can be almost any level in the S 0 manifold. S 1: 1 st excited electronic state manifold Pump Transition Metastable state Laser Transitions S 0: Ground electronic state manifold Dyes, for example, are such ideal four-level systems that it’s often difficult to stop them from lasing in all directions!

Dye Lasers Dye lasers are an ideal four-level system, and a given dye will lase over a range of ~100 nm.

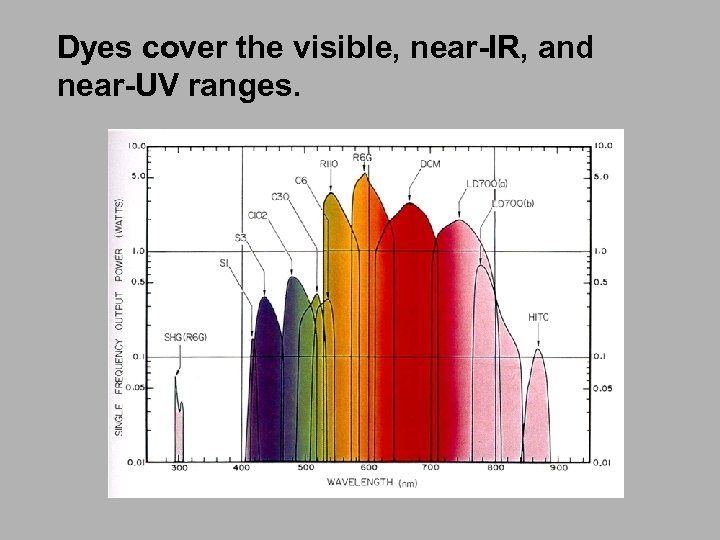
Dyes cover the visible, near-IR, and near-UV ranges.

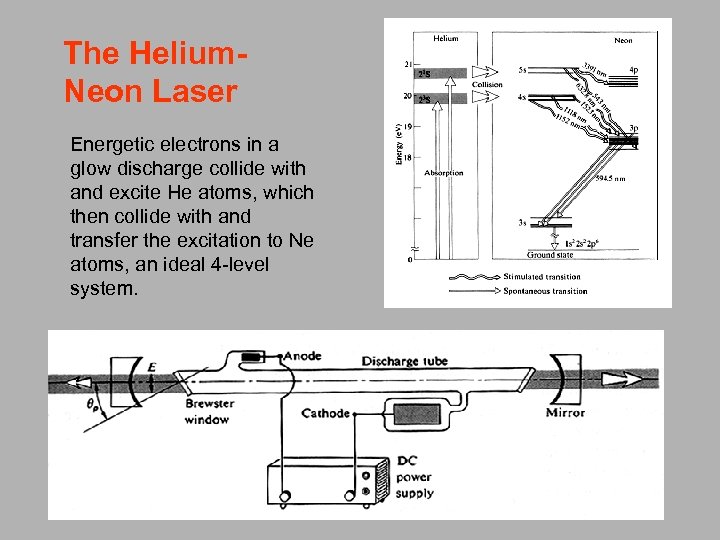
The Helium. Neon Laser Energetic electrons in a glow discharge collide with and excite He atoms, which then collide with and transfer the excitation to Ne atoms, an ideal 4 -level system.

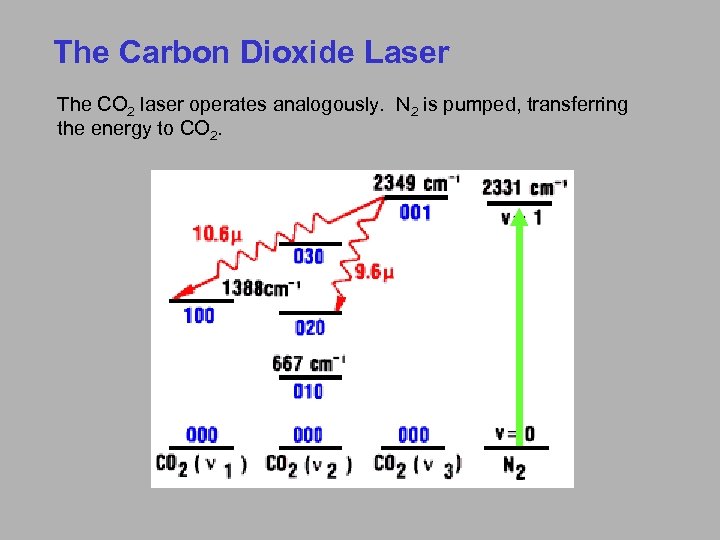
The Carbon Dioxide Laser The CO 2 laser operates analogously. N 2 is pumped, transferring the energy to CO 2.

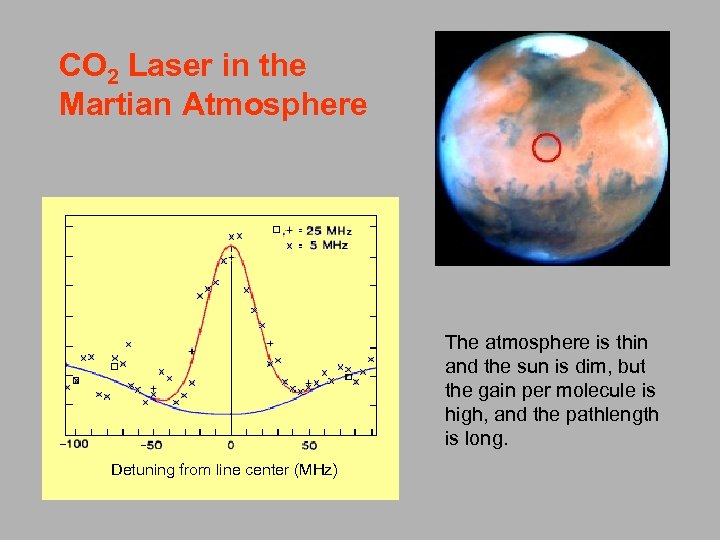
CO 2 Laser in the Martian Atmosphere The atmosphere is thin and the sun is dim, but the gain per molecule is high, and the pathlength is long. Detuning from line center (MHz)

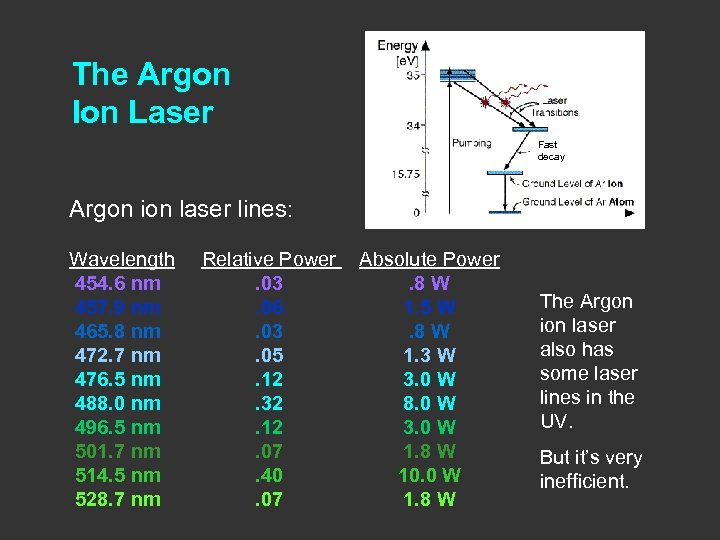
The Argon Ion Laser Fast decay Argon ion laser lines: Wavelength 454. 6 nm 457. 9 nm 465. 8 nm 472. 7 nm 476. 5 nm 488. 0 nm 496. 5 nm 501. 7 nm 514. 5 nm 528. 7 nm Relative Power Absolute Power . 03. 8 W. 06 1. 5 W. 03. 8 W. 05 1. 3 W. 12 3. 0 W. 32 8. 0 W. 12 3. 0 W. 07 1. 8 W. 40 10. 0 W. 07 1. 8 W The Argon ion laser also has some laser lines in the UV. But it’s very inefficient.

The Krypton Ion Laser Krypton ion laser lines: Wavelength 406. 7 nm 413. 1 nm 415. 4 nm 468. 0 nm 476. 2 nm 482. 5 nm 520. 8 nm 530. 9 nm 568. 2 nm 647. 1 nm 676. 4 nm Power . 9 W 1. 8 W. 28 W. 5 W. 4 W. 7 W 1. 5 W 1. 1 W 3. 5 W 1. 2 W

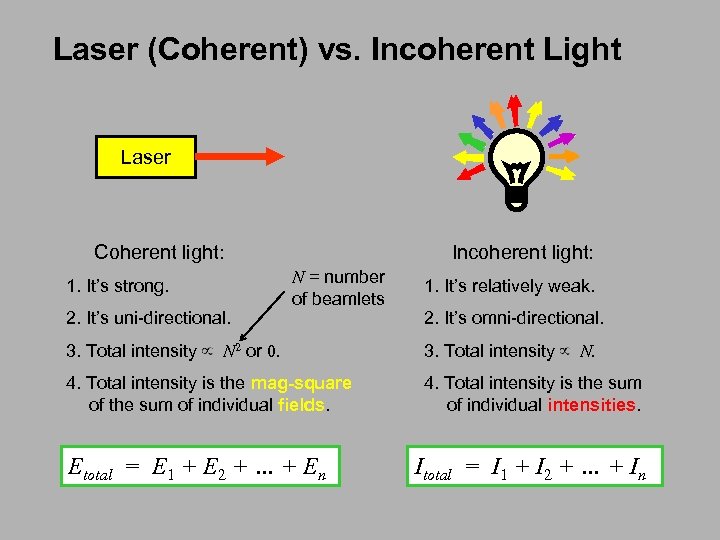
Laser (Coherent) vs. Incoherent Light Laser Coherent light: 1. It’s strong. 2. It’s uni-directional. Incoherent light: N = number of beamlets 1. It’s relatively weak. 2. It’s omni-directional. 3. Total intensity N 2 or 0. 3. Total intensity N. 4. Total intensity is the mag-square of the sum of individual fields. 4. Total intensity is the sum of individual intensities. Etotal = E 1 + E 2 + … + En Itotal = I 1 + I 2 + … + In