Black-Scholes Equation April 15, 2008
Contents • Options • Black Scholes PDE • Solution Method 1
Derivatives • There are many financial instruments, stocks, bonds, … • A derivative is a financial instrument whose value is derived from the value of some other instrument(s) • Forward contract: an agreement now to receive a specified goods at a future time and at a specified price. • Swap: agreement to exchange certain commodities • Option: 2
Options • European Option: At a pre-specified time, called the expiry or expiration date, T, the holder of the option has the right, but not the obligation, to exchange a prespecified asset, called the underlying asset, S, at a prespecified price, called the strike, K. • European Call Option: Buy the asset, pay the strike. • European Put Option: Sell the asset, receive the strike. • American Option: exercise can take place any time before the expiration date. 3
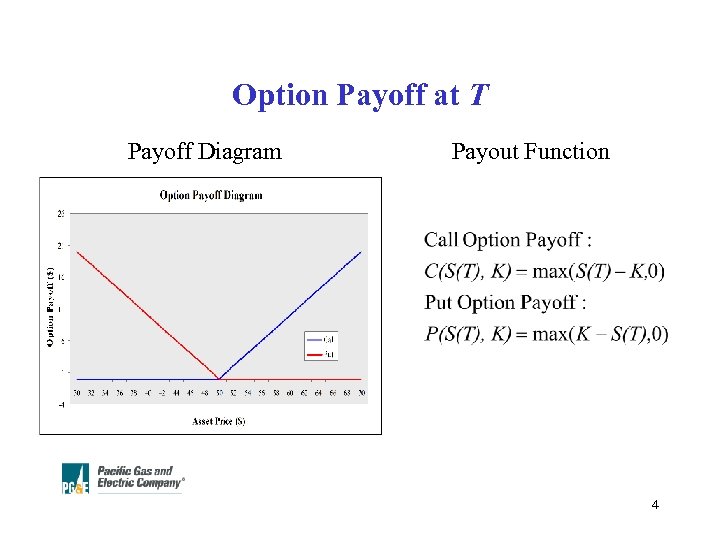
Option Payoff at T Payoff Diagram Payout Function 4
Why PG&E cares about Option Value • Serving the load: Load varies from forecast, option gives one the flexibility to cover the shortfalls. • Hedging risks: Reduces the risks of load and prices. • Reducing cost: Less expensive way to serve the load. 5
Option Value • The value of the option depends on T, K, risk-free discount rate r, and assumptions on S. • Bachelier’s assumption (1900): change in S is a random walk. • Black-Scholes assumed where m is called the drift, s is the volatility, both constants, and d. X is a normally distributed random variable with mean 0 and variance dt. 6
Black-Scholes Equation • With the above assumptions, Black and Scholes derived that, for any option whose value V(S, t) depending on S and t only, V(S, t) satisfies (1) • The terminal conditions for Call and Put are • The boundary conditions for Call and Put are 7
Black-Scholes Solution • To solve equation (1), we make the following change of variables: • This leads to the following (2) 8
Black-Scholes Solution • To further simplify the equation, let • We get • Choosing Equation (2) becomes the heat equation (3) 9
Black-Scholes Solution • The heat equation has the solution (4) where • For Call, we have • Substituting the initial condition in (4) yields the value of the call option. 10
Black-Scholes Solution • Finally, (5) where 11
Black-Scholes Solution • Using the simple, distribution free relation the value of put can be found as • Combining with equation (5) we can write where h=1 if it is a call, h=-1 if it is a put. 12
American Option • For American Option, the same differential equation, terminal condition and boundary conditions hold • To permit early exercise, we impose • Analytical solution? 13
References 1. F. Black, M. Scholes, The pricing of options and corporate liabilities, Jour. Political Economy, vol. 81 (1973), pp. 637 -654. 2. P. Wilmott, S. Howison, J. Dewynne, The Mathematics of Financial Derivatives, A Student Introduction, Cambridge University Press, 1995. 14
Скачать презентацию Black-Scholes Equation April 15 2008 Contents
1580bb944ed9460254ae0914ff8579dc.ppt