Black-box oracle Feed me a weighted graph G

Black-box (oracle) Feed me a weighted graph G and I will tell you the weight of the max-weight matching of G.

Black-box (oracle) 5 2 2 Feed me a weighted graph G and I will tell you the weight of the max-weight matching of G.

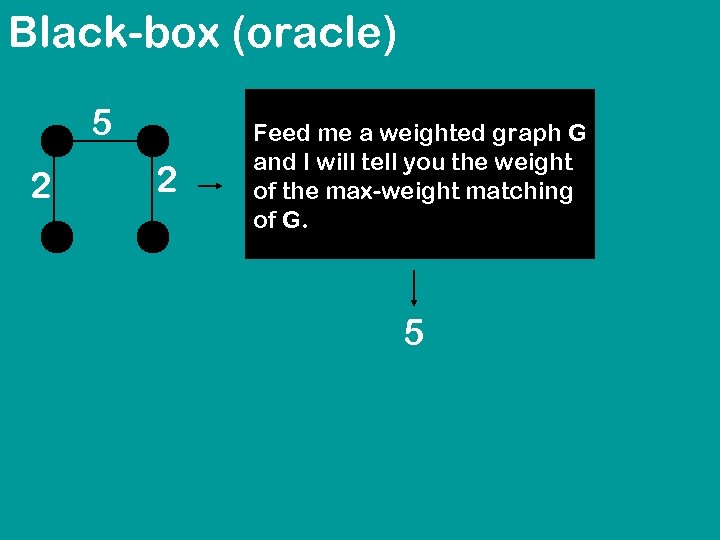
Black-box (oracle) 5 2 2 Feed me a weighted graph G and I will tell you the weight of the max-weight matching of G. 5

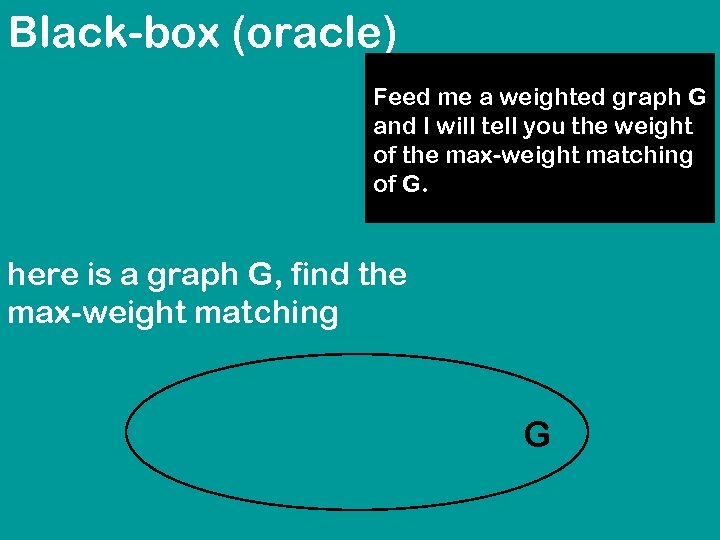
Black-box (oracle) Feed me a weighted graph G and I will tell you the weight of the max-weight matching of G. here is a graph G, find the max-weight matching G

Black-box (oracle) here is a graph G, find the max-weight matching Feed me a weighted graph G and I will tell you the weight of the max-weight matching of G. pick a vertex u V(G) for each edge {u, v} E(G) w undefined if oracle(G-u-v) + w(u, v) = oracle (G) then w v if w is undefined then recurse on (G-u) else print({u, w}); recurse on (G-u-v)

3 -SAT x = variable x = negation of a variable literals clause = disjunction of literals x y z x z

3 -SAT INSTANCE: collection C of clauses, each clause has at most 3 literals QUESTION: does there exist an assignment of true/false to the variables which satisfies all the clauses in C

3 -SAT INSTANCE: collection C of clauses, each clause has at most 3 literals QUESTION: does there exist an assignment of true/false to the variables which satisfies all the clauses in C x y z x y x

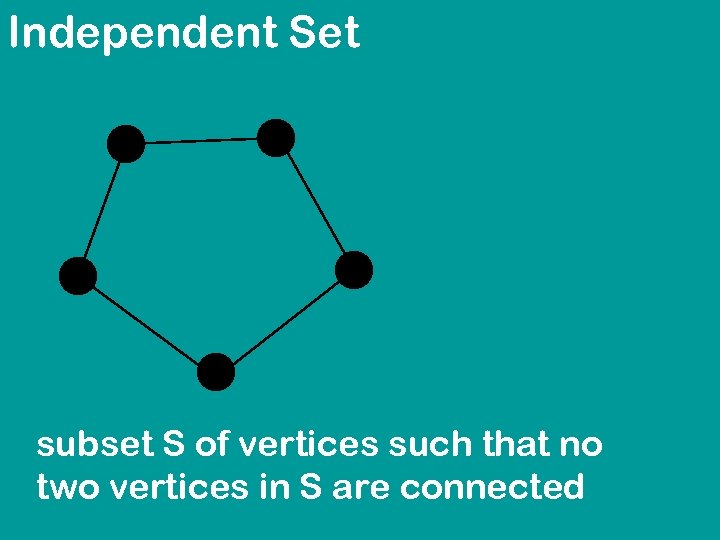
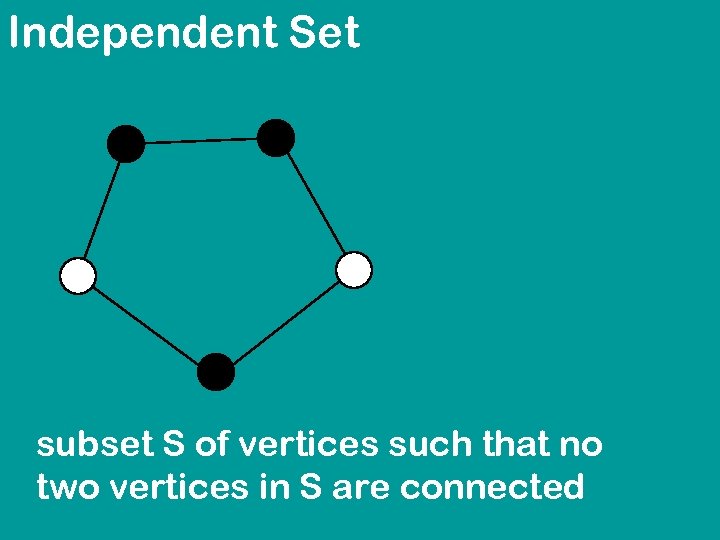
Independent Set subset S of vertices such that no two vertices in S are connected

Independent Set OPTIMIZATION VERSION: INSTANCE: graph G SOLUTION: independent set S in G MEASURE: maximize the size of S DECISION VERSION: INSTANCE: graph G, number K QUESTION: does G have independent set of size K

Independent Set 3 -SAT “is easier than” if we have a black-box for 3 -SAT then we can solve Independent Set in polynomial time Independent Set reduces to 3 -SAT

Independent Set 3 -SAT if we have a black-box for 3 -SAT then we can solve Independent Set in polynomial time Give me a 3 -SAT formula and I will tell you if it is satisfiable We would like to solve the Independent Set problem using the black box in polynomial time.

Independent Set 3 -SAT Give me a 3 -SAT formula and I will tell you if it is satisfiable Graph G, K 3 -SAT formula F efficient transformation (i. e. , polynomial – time) G has independent set of size K F is satisfiable

Independent Set 3 -SAT Give me a 3 -SAT formula and I will tell you if it is satisfiable Graph G, K V = {1, . . . , n} E = edges 3 -SAT formula F variables x 1, . . , xn xi xj for ij E + we need to ensure that K of the xi are TRUE

3 -SAT Independent Set Give me a graph G and a number K and I will tell you if G has independent set of size K 3 -SAT formula F graph G, number K

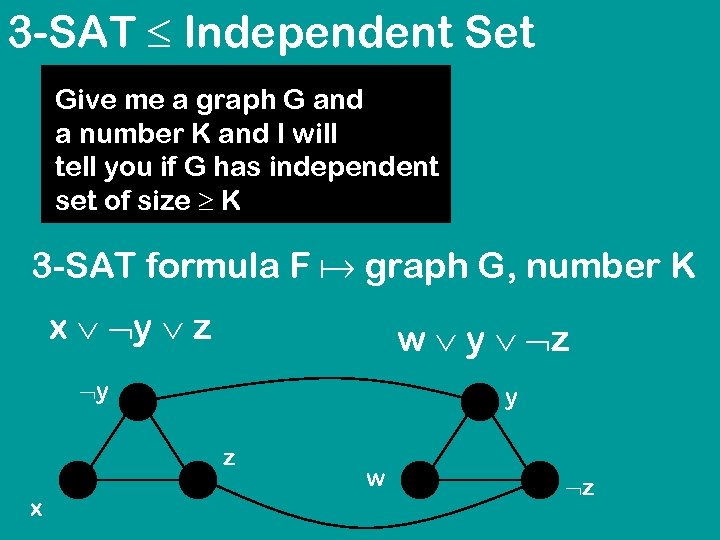
3 -SAT Independent Set Give me a graph G and a number K and I will tell you if G has independent set of size K 3 -SAT formula F graph G, number K x y z w y z y y z x w z

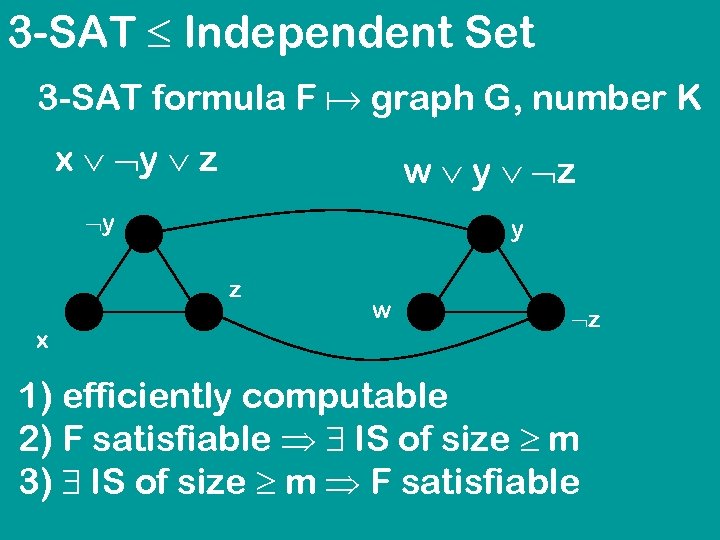
3 -SAT Independent Set 3 -SAT formula F graph G, number K x y z w y z y y z x w z 1) efficiently computable 2) F satisfiable IS of size m 3) IS of size m F satisfiable

3 -SAT Independent Set 3 -SAT if 3 -SAT is in P then Independent Set is in P if Independent Set is in P then 3 -SAT is in P 3 -SAT Independent Set

Many more reductions Clique Subset-Sum 3 -COL Planar 3 -COL Hamiltonian path 3 -SAT Independent Set

P and NP P = decision problems that can be solved in polynomial time. NP = decision problems for which the YES answer can be certified and this certificate can be verified in polynomial time.

NP = decision problems for which the YES answer can be certified and this certificate can be verified in polynomial time. 3 -SAT Independent Set NOT-3 -SAT ?

NP = decision problems for which the YES answer can be certified and this certificate can be verified in polynomial time. COOK’S THEOREM Every problem A NP A 3 -SAT

NP = decision problems for which the YES answer can be certified and this certificate can be verified in polynomial time. B is NP-hard if every problem A NP A B B is NP-complete if B is NP-hard, and B is in NP

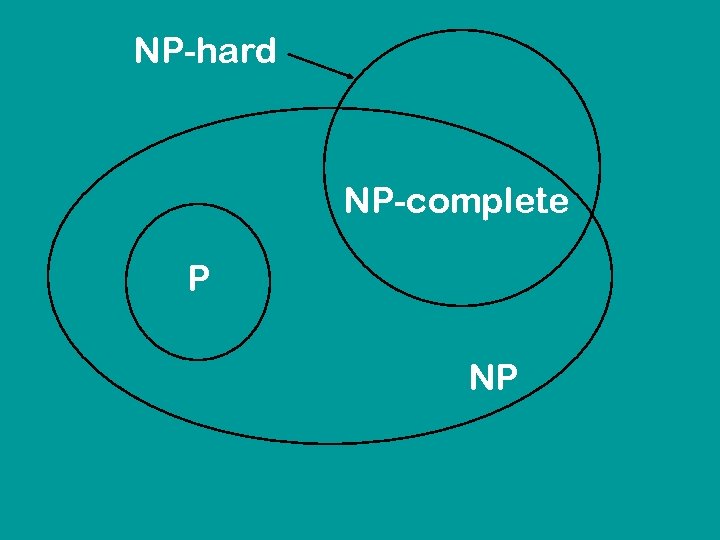
NP-hard NP-complete P NP

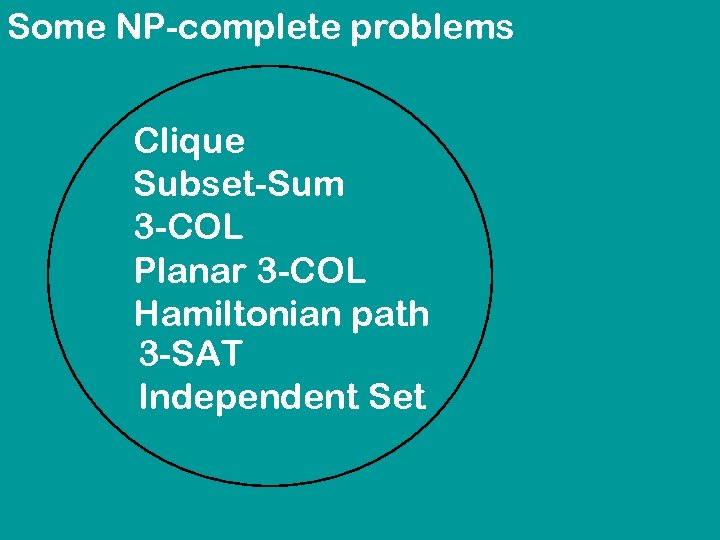
Some NP-complete problems Clique Subset-Sum 3 -COL Planar 3 -COL Hamiltonian path 3 -SAT Independent Set

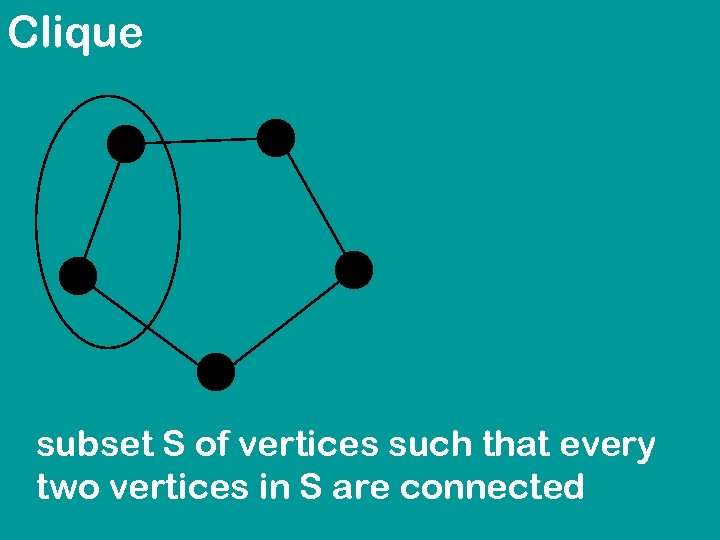
Clique subset S of vertices such that every two vertices in S are connected

Clique INSTANCE: graph G, number K QUESTION: does G have a clique of size K?

Subset-Sum INSTANCE: numbers a 1, . . . , an, B QUESTIONS: is there S {1, . . . , n} such that a =B i S i

3 -COL INSTANCE: graph G QUESTION: can the vertices of G be assigned colors red, green, blue so that no two neighboring vertices have the same color?

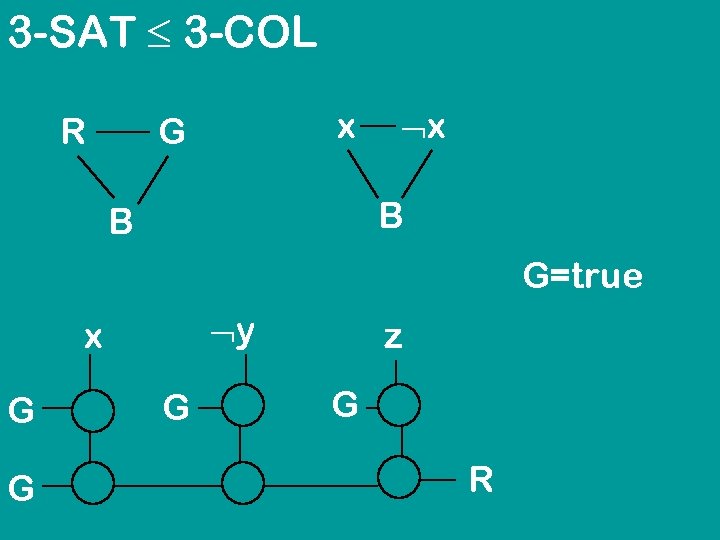
3 -SAT 3 -COL R x G x B B G=true y x G G G z G R

Planar-3 -COL INSTANCE: planar graph G QUESTION: can the vertices of G be assigned colors red, green, blue so that no two neighboring vertices have the same color?

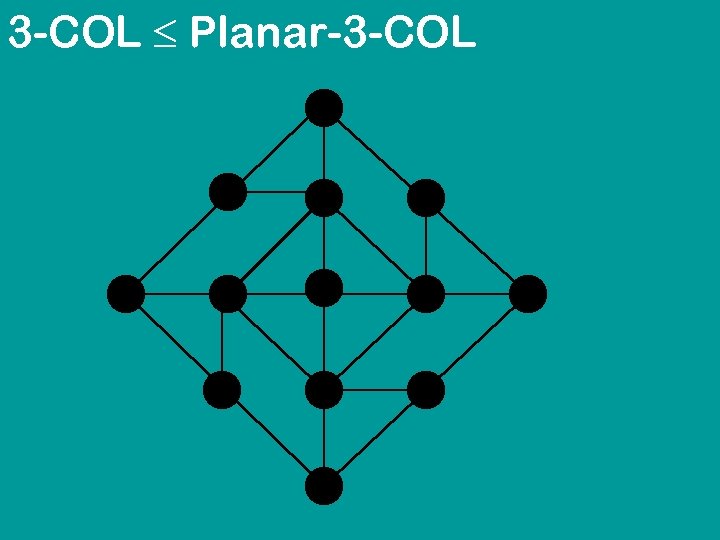
3 -COL Planar-3 -COL

4 -COL INSTANCE: graph G QUESTION: can the vertices of G be assigned one of 4 colors so that no two neighboring vertices have the same color?

3 -COL 4 -COL

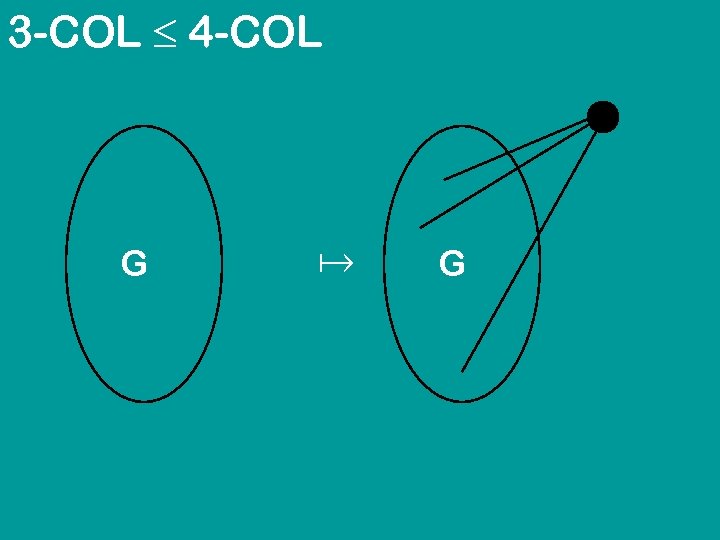
3 -COL 4 -COL G G

planar 4 -COL INSTANCE: planar graph G QUESTION: can the vertices of G be assigned one of 4 colors so that no two neighboring vertices have the same color? planar 3 -COL planar 4 -COL ? ? ?

4 -COL 3 -COL 4 -COL NP Cook 4 -COL 3 -SAT 3 -COL Thus: 4 -COL 3 -COL

2 -COL 3 -COL

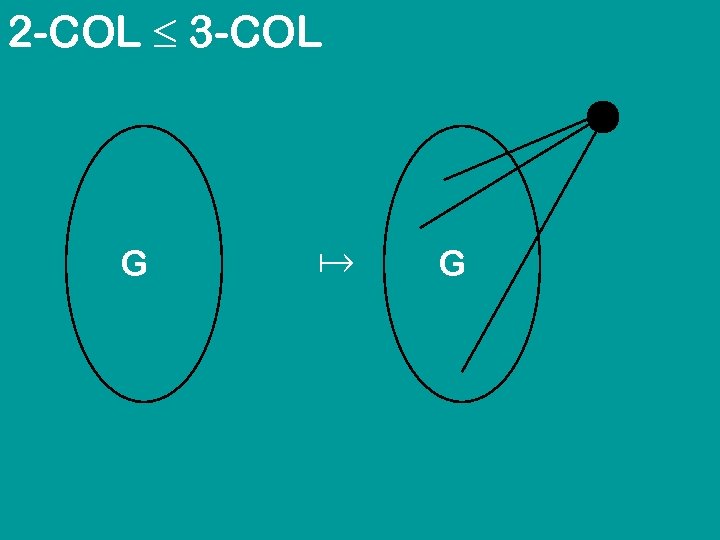
2 -COL 3 -COL G G

3 -COL 2 -COL ? ? ? 2 -COL in P