352b326ca55c80f6d3fad2f4989dd209.ppt
- Количество слайдов: 51

Black Box and Generalized Algorithms for Planning in Uncertain Domains Thesis Proposal, Dept. of Computer Science, Carnegie Mellon University H. Brendan Mc. Mahan 1

Outline n The Problem and Approach Motivating Examples ¨ Goals and Techniques ¨ MDPs and Uncertainty ¨ n n Example Algorithms Proposed Future Work 2

Mars Rover Mission Planning Human control not realistic n Collect data while conserving power and bandwidth n First Experiments in the Robotic Investigation of Life in the Atacama Desert of Chile. D. Wettergreen, et al. 2005. Recent Progress in Local and Global Traversability for Planetary Rovers. S. Singh, et al. 2000. 3

Autonomous Helicopter Control 6+ continuous state dimensions n Complex, non-linear dynamics n High failure cost n Inverted Autonomous Helicopter Flight via Reinforcement Learning A. Ng, et al. Autonomous Helicopter Control using Reinforcement Learning Policy Search Methods J. Bagnell and J. Schneider 4
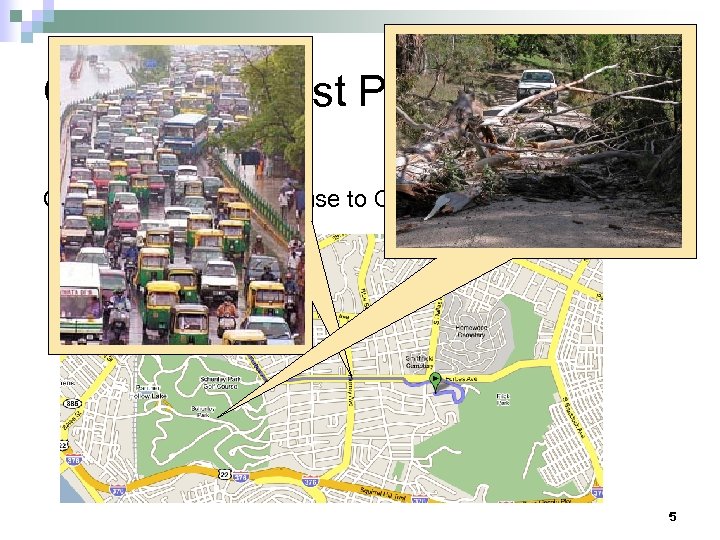
Online Shortest Path Problem Getting from my (old) house to CMU each day: 5

Other Domains 6

Goal Planning n multiple decisions over time to achieve goals or minimize cost in Uncertain Domains n NOT deterministic, fully observable, perfectly modeled 7
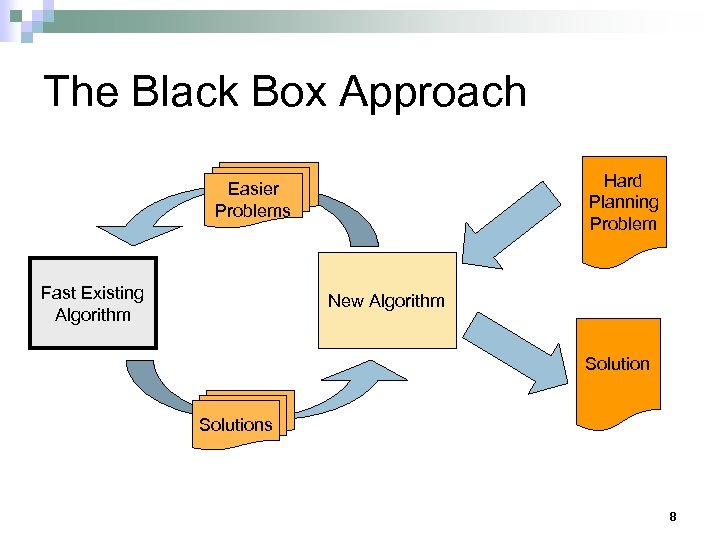
The Black Box Approach Hard Planning Problem Easier Problems Fast Existing Algorithm New Algorithm Solutions 8
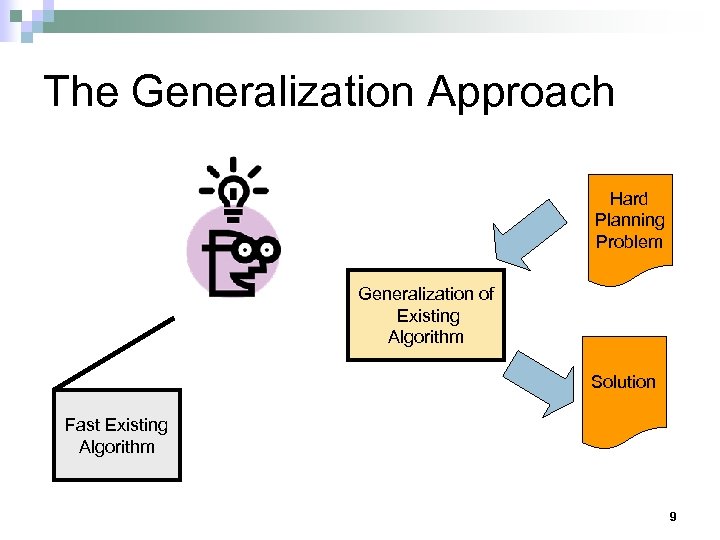
The Generalization Approach Hard Planning Problem Generalization of Existing Algorithm Solution Fast Existing Algorithm 9
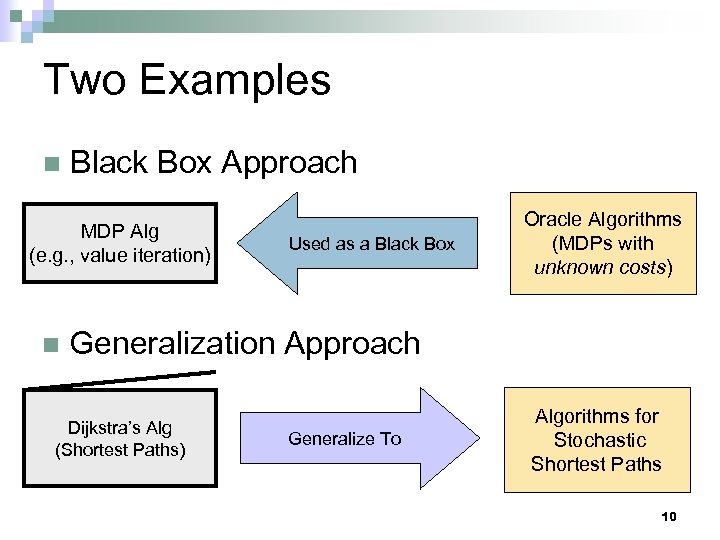
Two Examples n Black Box Approach MDP Alg (e. g. , value iteration) n Used as a Black Box Oracle Algorithms (MDPs with unknown costs) Generalization Approach Dijkstra’s Alg (Shortest Paths) Generalize To Algorithms for Stochastic Shortest Paths 10

Benefits of using Black Boxes n Use fast/optimized/mature implementations n Pick implementation for specific domain n Will be able to use algorithms not even invented yet n Theoretical advantages 11
Benefits of Generalization New intuitions n Some performance guarantees for free n 12
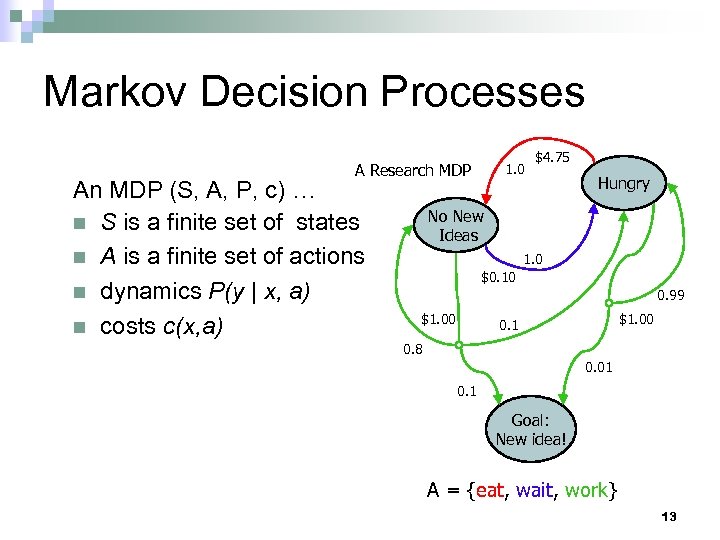
Markov Decision Processes A Research MDP An MDP (S, A, P, c) … n S is a finite set of states n A is a finite set of actions n dynamics P(y | x, a) n costs c(x, a) 1. 0 $4. 75 Hungry No New Ideas 1. 0 $0. 10 0. 99 $1. 00 0. 1 0. 8 0. 01 0. 1 Goal: New idea! A = {eat, wait, work} 13
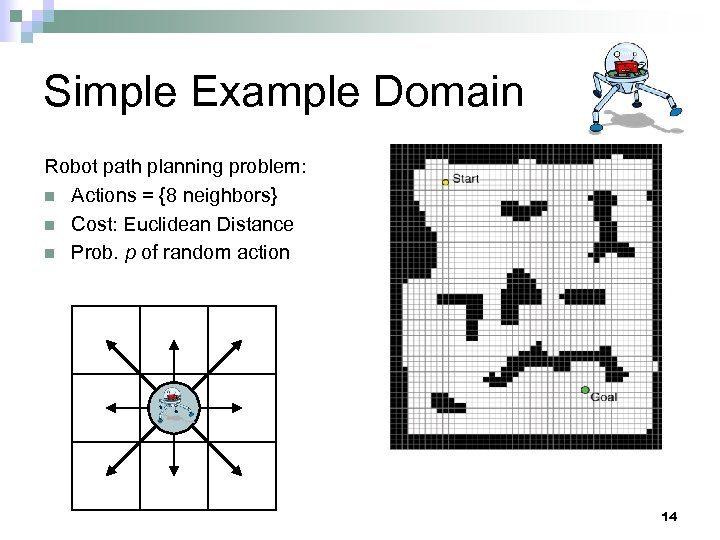
Simple Example Domain Robot path planning problem: n Actions = {8 neighbors} n Cost: Euclidean Distance n Prob. p of random action 14

Types of Uncertainty Outcome Uncertainty (MDPs) n Partial Observability (POMDPs) n Model Uncertainty (families of MDPs, RL) n n Modeling Other Agents (Agent Uncertainty? ) 15

The Curse of Dimensionality n The size of |S| is exponential in the number of state variables: <x, y, vx, vy, battery_power, door_open, another_door_open, goal_x, goal_y, bob_x, bob_y, …> 16

Outline n n The Problem and Approach Example Algorithms MDPs with Unknown Costs ¨ Generalizing Dijkstra’s Algorithm ¨ n Proposed Future Work 17

Unknown Costs, Offline Version A game with two players: n The Planner chooses a policy for a MDP with known dynamics n The Sentry chooses a cost function from a set K = {c 1, …, ck} of possible cost functions. 18
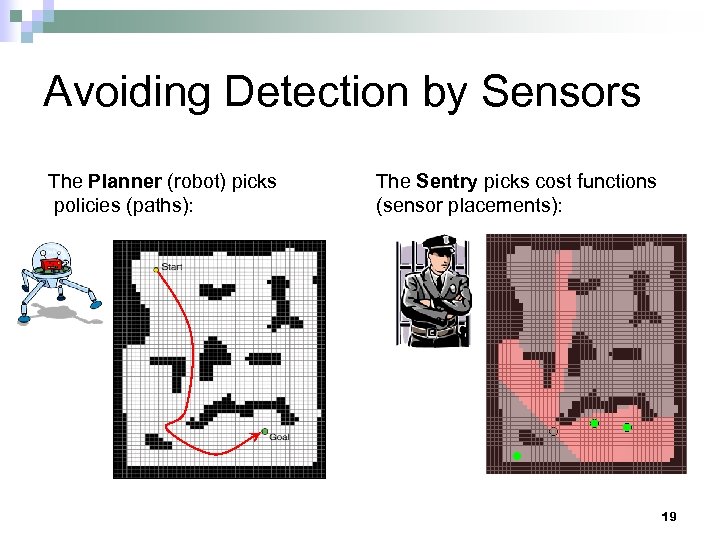
Avoiding Detection by Sensors The Planner (robot) picks policies (paths): The Sentry picks cost functions (sensor placements): 19
Matrix Game Formulation An optimal mixed strategy for Matrix game M: a distribution the planner is n Planner (rows) selects a policy over deterministic polices (paths). n Sentry (columns) selects a cost c n M( , c) = [total cost of under costs c] Goal: Find a minimax solution to M 20

Interpretations Model Uncertainty: → unknown cost function n Partial Observability: → fixed, unobservable cost function n Agent Uncertainty: → an adversary picks the cost function n 21

How to Solve It n Problem: Matrix M is exponentially big n Solution: Can be represented compactly as a Linear Program (LP) n Problem: LP still takes much too long to solve Solution: The Single Oracle Algorithm, taking advantage of fast black box MDP algorithms n 22

Single Oracle Algorithm F is a small set of policies n M’ is the matrix game where the Planner must play from F. n n We can solve M’ efficiently, it is only |F| x |K| in size! |F| = 2 23

Single Oracle Algorithm If only … n we knew it was sufficient for the Planner to randomize among a small set of strategies n and we could find that set of strategies. 24
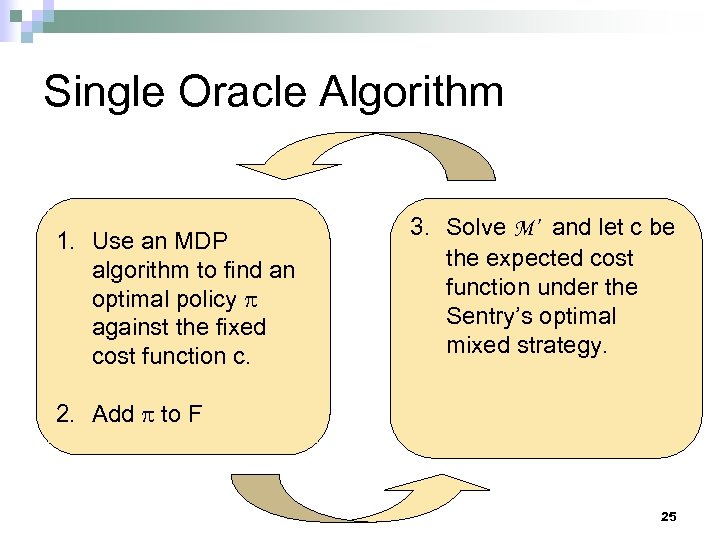
Single Oracle Algorithm 1. Use an MDP algorithm to find an optimal policy against the fixed cost function c. 3. Solve M’ and let c be the expected cost function under the Sentry’s optimal mixed strategy. 2. Add to F 25
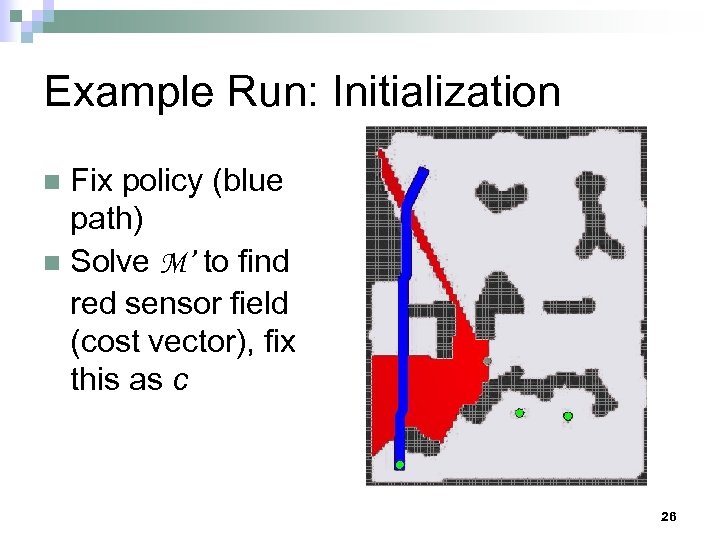
Example Run: Initialization Fix policy (blue path) n Solve M’ to find red sensor field (cost vector), fix this as c n 26
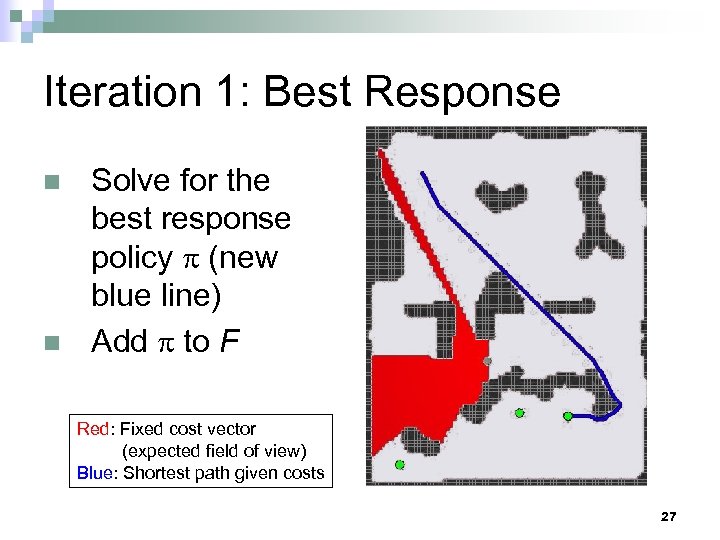
Iteration 1: Best Response n n Solve for the best response policy (new blue line) Add to F Red: Fixed cost vector (expected field of view) Blue: Shortest path given costs 27
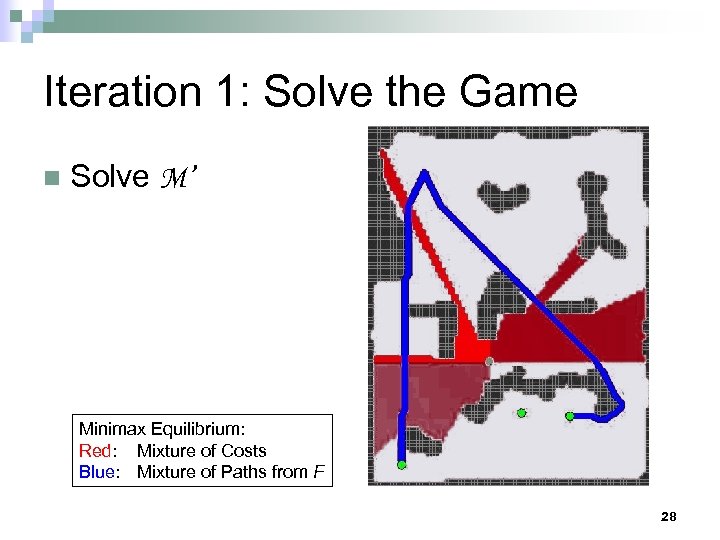
Iteration 1: Solve the Game n Solve M’ Minimax Equilibrium: Red: Mixture of Costs Blue: Mixture of Paths from F 28
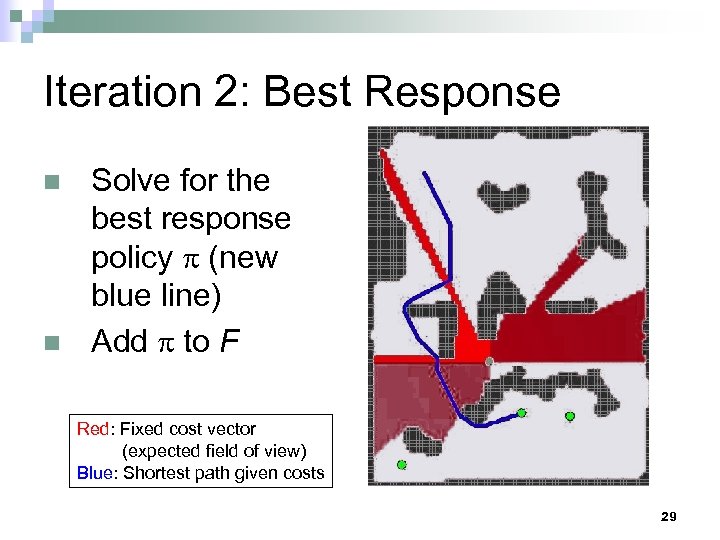
Iteration 2: Best Response n n Solve for the best response policy (new blue line) Add to F Red: Fixed cost vector (expected field of view) Blue: Shortest path given costs 29
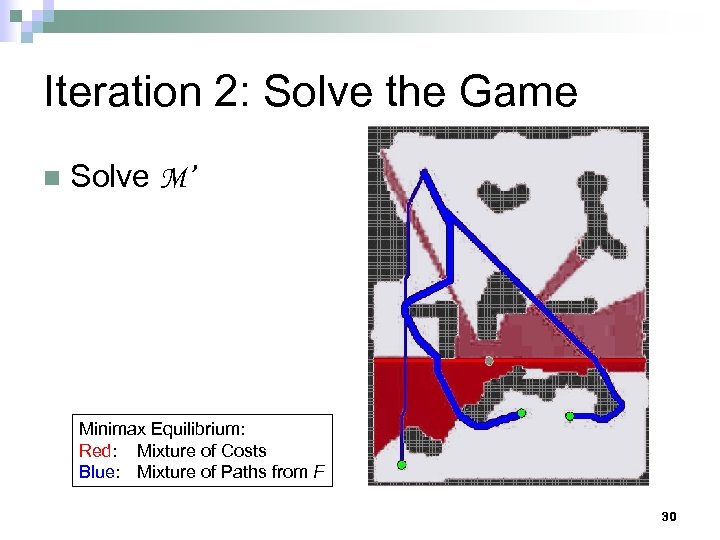
Iteration 2: Solve the Game n Solve M’ Minimax Equilibrium: Red: Mixture of Costs Blue: Mixture of Paths from F 30
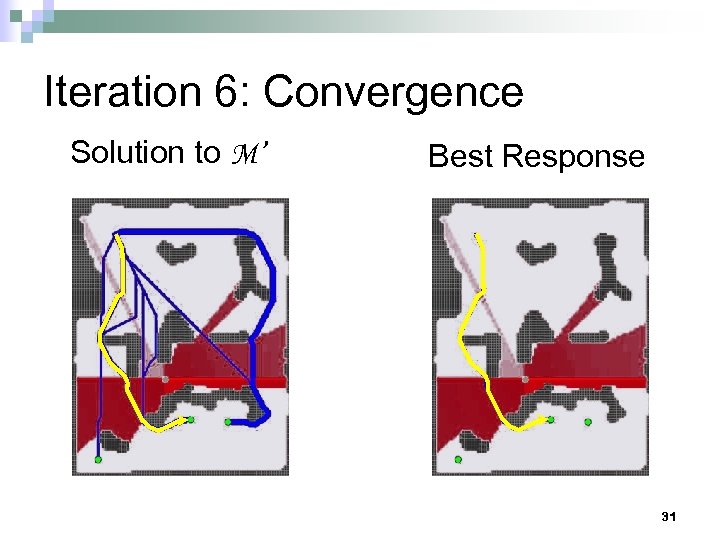
Iteration 6: Convergence Solution to M’ Best Response 31

Unknown Costs, Online Version Go from my house to CMU each day n Model as a graph n 32
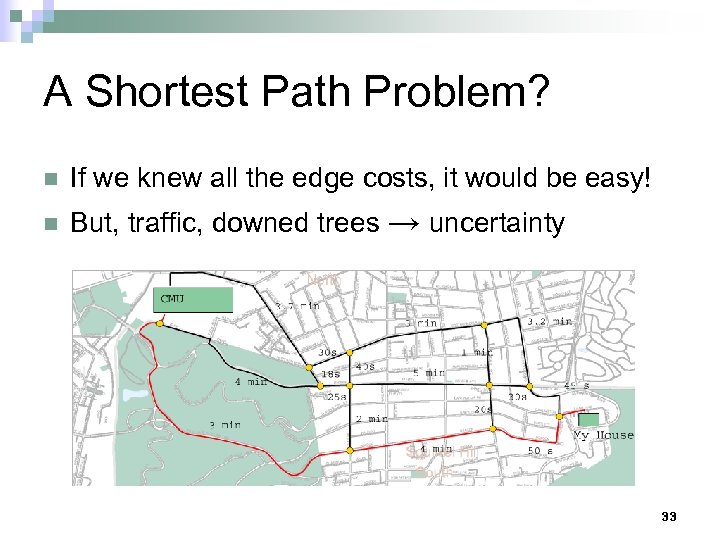
A Shortest Path Problem? n If we knew all the edge costs, it would be easy! n But, traffic, downed trees → uncertainty 33

BGA Algorithm: Limited Observations Keep estimates of edge lengths n • Most days, follow of algorithm: Each day, observe the total length. FPL 1 the path pick shortest path with respect to estimated we actually took to get to CMU little noise. lengths plus a • Occasionally, play a “random” path in order to make sure we have good estimates of the edge lengths. 1 [Kalai and Vempala, 2003] 34
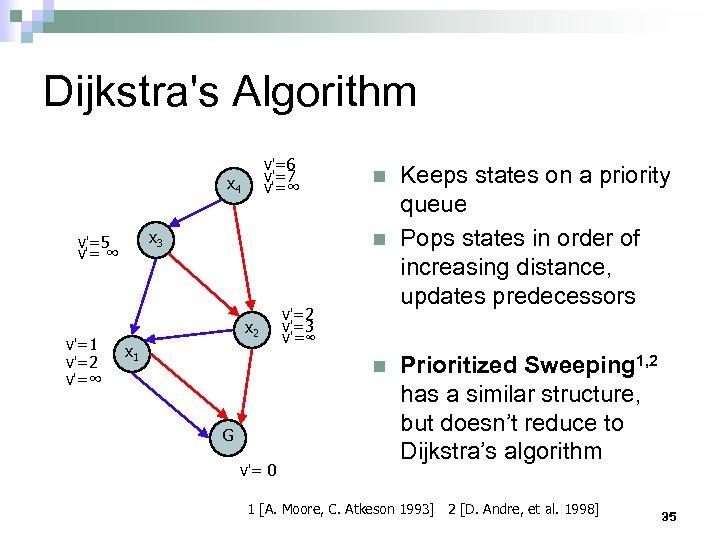
Dijkstra's Algorithm v'=6 v'=7 v'=∞ x 4 x 3 v'=5 v'= ∞ v'=1 v'=2 v'=∞ n n x 2 x 1 v'=2 v'=3 v'=∞ n G v'= 0 Keeps states on a priority queue Pops states in order of increasing distance, updates predecessors Prioritized Sweeping 1, 2 has a similar structure, but doesn’t reduce to Dijkstra’s algorithm 1 [A. Moore, C. Atkeson 1993] 2 [D. Andre, et al. 1998] 35
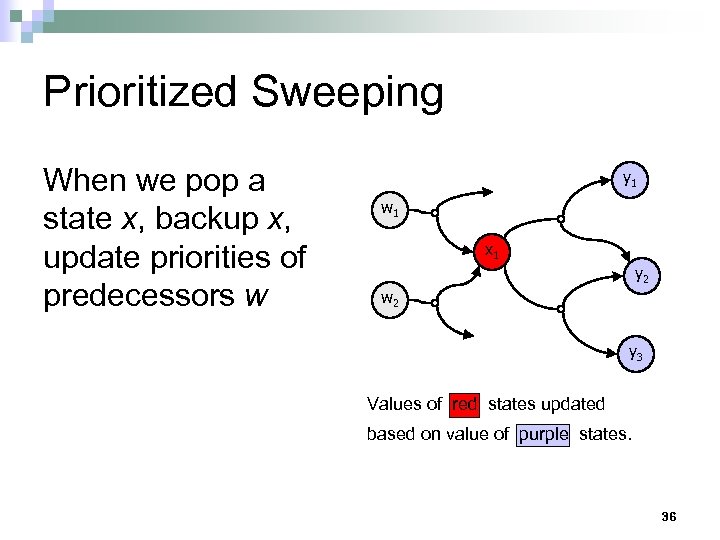
Prioritized Sweeping When we pop a state x, backup x, update priorities of predecessors w y 1 w 1 x 1 y 2 w 2 y 3 Values of red states updated based on value of purple states. 36
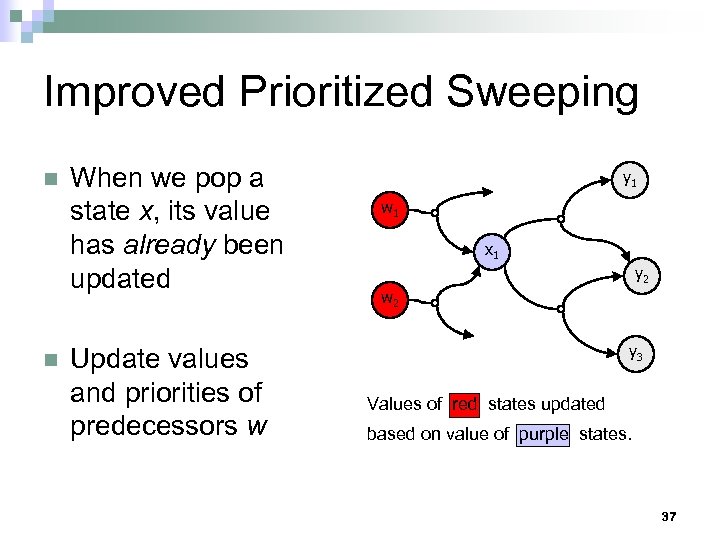
Improved Prioritized Sweeping n n When we pop a state x, its value has already been updated Update values and priorities of predecessors w y 1 w 1 x 1 y 2 w 2 y 3 Values of red states updated based on value of purple states. 37

Priority Function Intuitions Update the state: n with lowest value (closest to goal) n whose value is most accurately known ¨ For Dijkstra’s algorithm, the updated (popped) state’s optimal value is known ¨ This is the state whose value will change the least in the future. n whose value has changed the most since it was last updated. 38
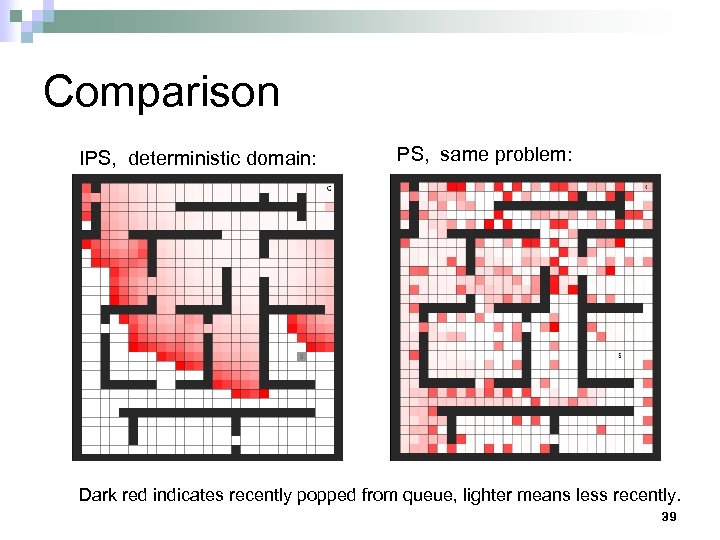
Comparison IPS, deterministic domain: PS, same problem: Dark red indicates recently popped from queue, lighter means less recently. 39

Outline n n n The Problem and Approach Example Algorithms Proposed Future Work Bounded RTDP and extensions ¨ Large action spaces ¨ Details of proposed contributions ¨ 40
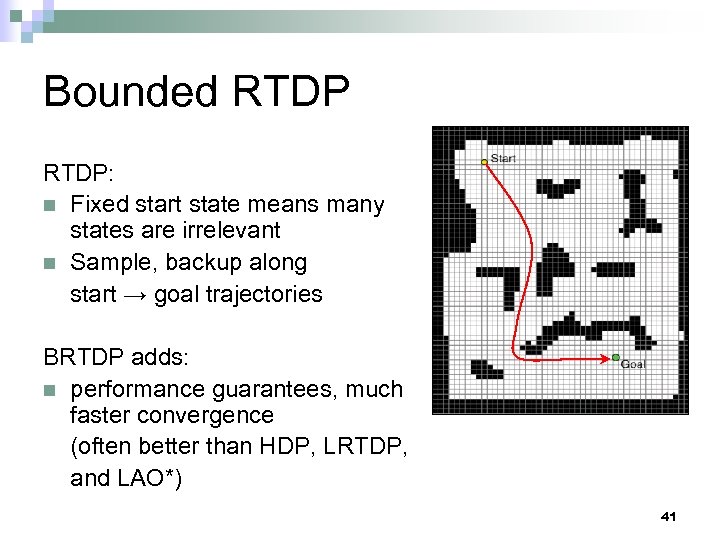
Bounded RTDP: n Fixed start state means many states are irrelevant n Sample, backup along start → goal trajectories BRTDP adds: n performance guarantees, much faster convergence (often better than HDP, LRTDP, and LAO*) 41

Dijkstra and BRTDP Dijkstra-style scheduling of backups for BRTDP n Sample multiple trajectories n Use priority queue to schedule backups of states on all trajectories 42
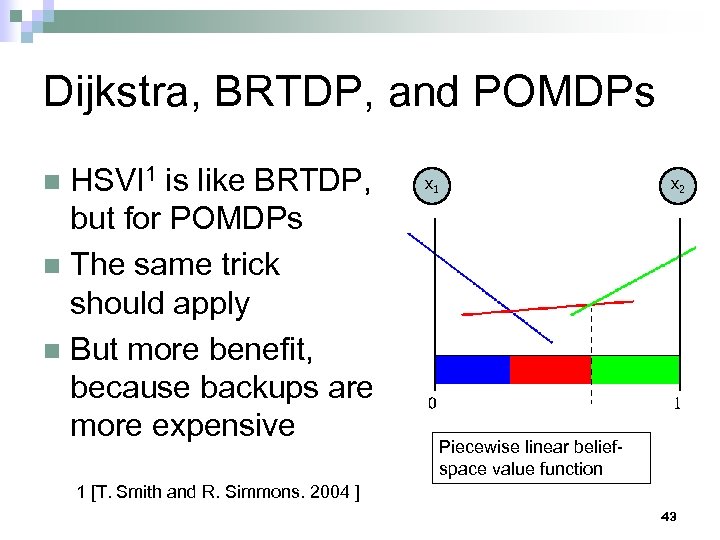
Dijkstra, BRTDP, and POMDPs HSVI 1 is like BRTDP, but for POMDPs n The same trick should apply n But more benefit, because backups are more expensive n x 1 x 2 Piecewise linear beliefspace value function 1 [T. Smith and R. Simmons. 2004 ] 43

Large Action Spaces n (Prioritized) Policy Iteration already has an advantage n Better tradeoff between policy evaluation, policy improvement? Structured sets of actions? Application of Experts/Bandits algorithms? n n 44

Details: Proposed Contributions n n Discussion of algorithms already developed: Oracle Algorithms, BGA, IPS, BRTDP, and several others. At least two significant new algorithmic contributions: BRTDP + Dijkstra algorithm, extension to POMDPs ¨ Improved version of PPI to handle large action spaces ¨ Something else: generalizations of conjugate-gradient linear solvers to MDPs, extensions of the technique for finding upper bounds introduced in the BRTDP paper, algorithms for efficiently solving restricted classes of POMDPs. . . ¨ 45

Details: Proposed Contributions n At least one significant new theoretical contribution: ¨ Approximation algorithm for Canadian Traveler’s Problem or Stochastic TSP ¨ Results connecting online algorithms / MDP techniques to stochastic optimization ¨ New contributions on bandit-style online algorithms, perhaps applications to MDPs 46
Summary Motivating Problems Generalization: Reducing to Dijkstra Black Boxes: MDPs with unknown Costs Future Work: BRTDP + Dijkstra, Large action spaces 47

Questions? 48
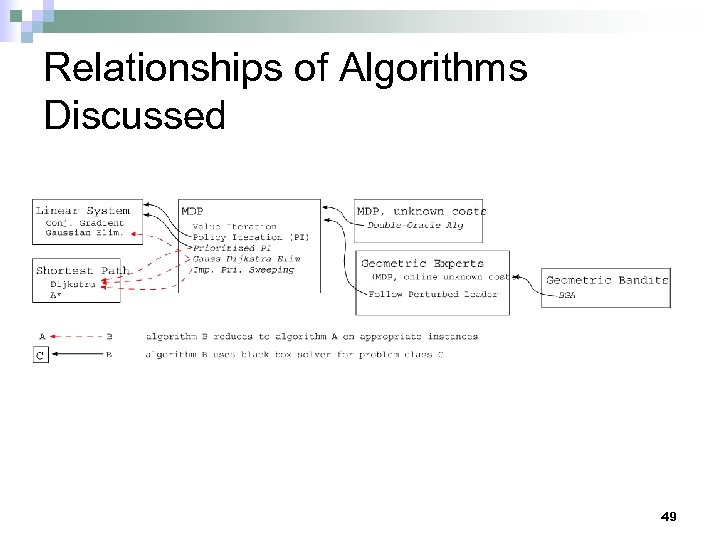
Relationships of Algorithms Discussed 49

Iteration 3: Best Response n n Solve for the best response policy (new blue line) Add to F Red: Fixed cost vector (expected field of view) Blue: Shortest path given costs 50
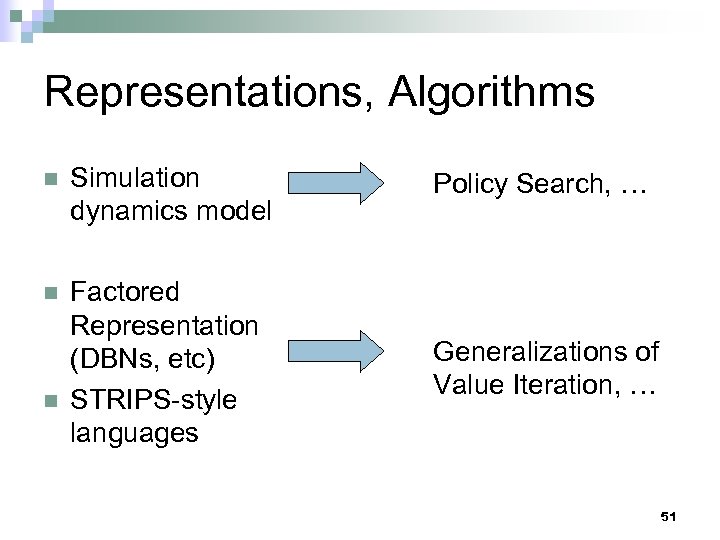
Representations, Algorithms n Simulation dynamics model Policy Search, … n Factored Representation (DBNs, etc) STRIPS-style languages Generalizations of Value Iteration, … n 51
352b326ca55c80f6d3fad2f4989dd209.ppt