252f4082c4b3eb1495dcef483add4b92.ppt
- Количество слайдов: 62

Black-body Radiation & the Quantum Hypothesis Max Planck Micro-world Macro-world Lect 13
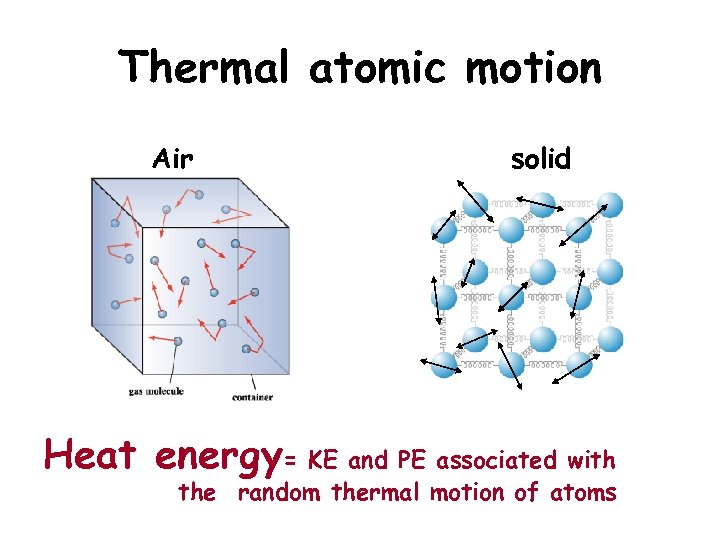
Thermal atomic motion Air solid Heat energy= KE and PE associated with the random thermal motion of atoms
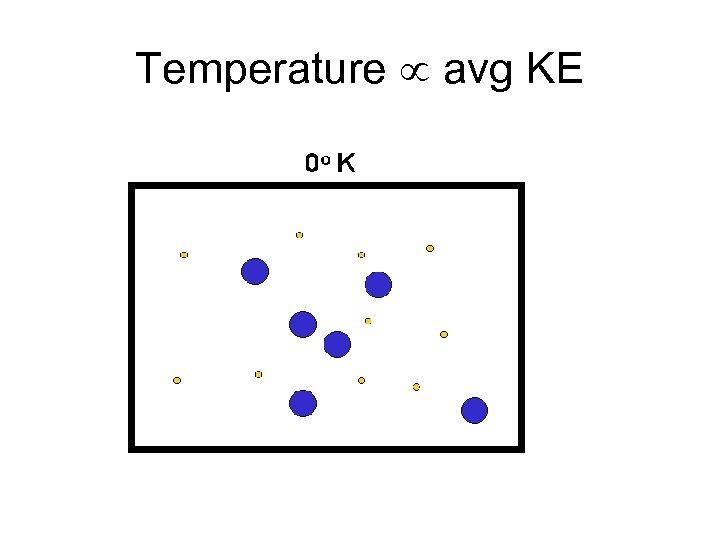
Temperature avg KE
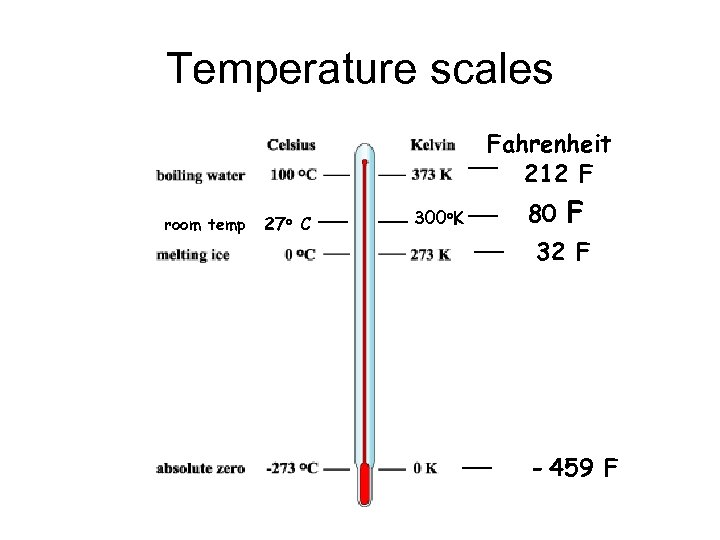
Temperature scales Fahrenheit 212 F room temp 27 o C 300 o. K 80 F 32 F - 459 F
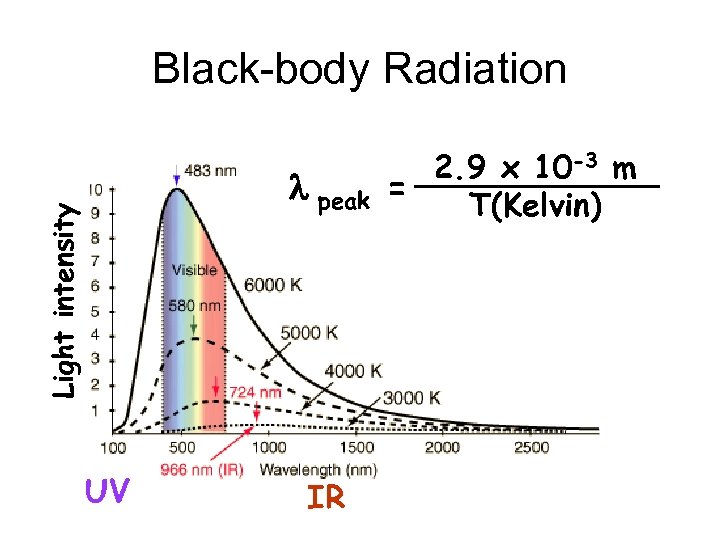
Black-body Radiation Light intensity l peak UV IR 2. 9 x 10 -3 m = T(Kelvin)
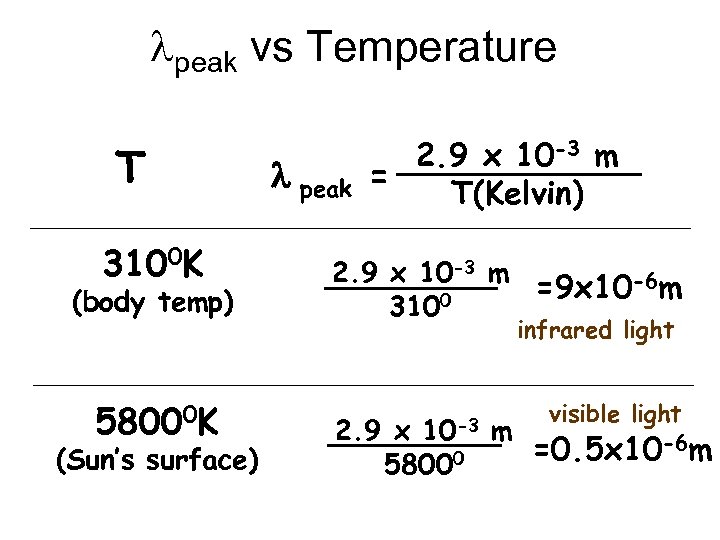
lpeak vs Temperature T 3100 K (body temp) 58000 K (Sun’s surface) l peak 2. 9 x 10 -3 m = T(Kelvin) 2. 9 x 10 -3 m =9 x 10 -6 m 3100 infrared light 10 -3 visible light 2. 9 x m =0. 5 x 10 -6 m 58000
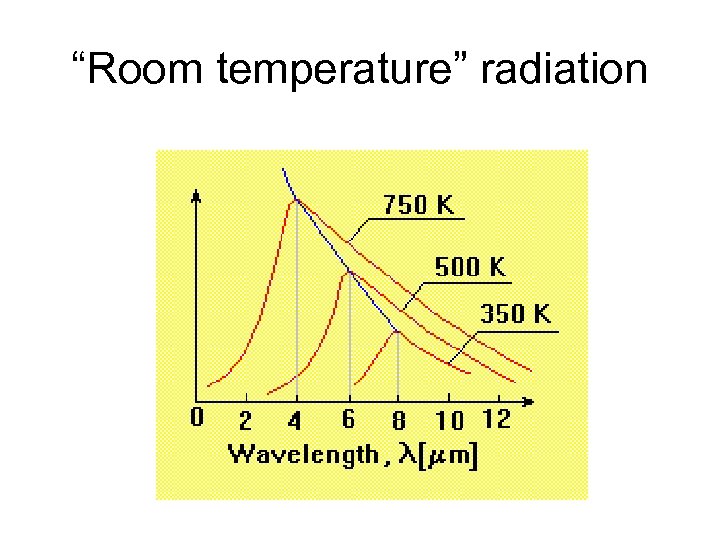
“Room temperature” radiation

Photo with an IR camera

IR Cat

IR house
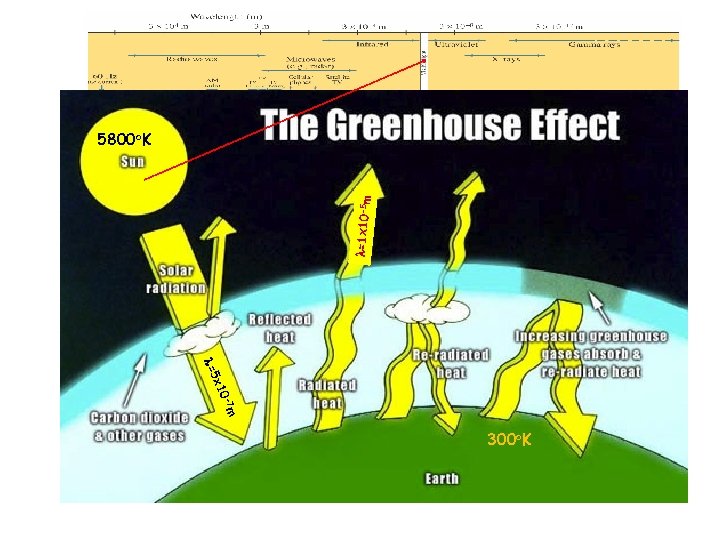
l=1 x 10 -5 m 5800 o. K -7 m x 10 l=5 300 o. K
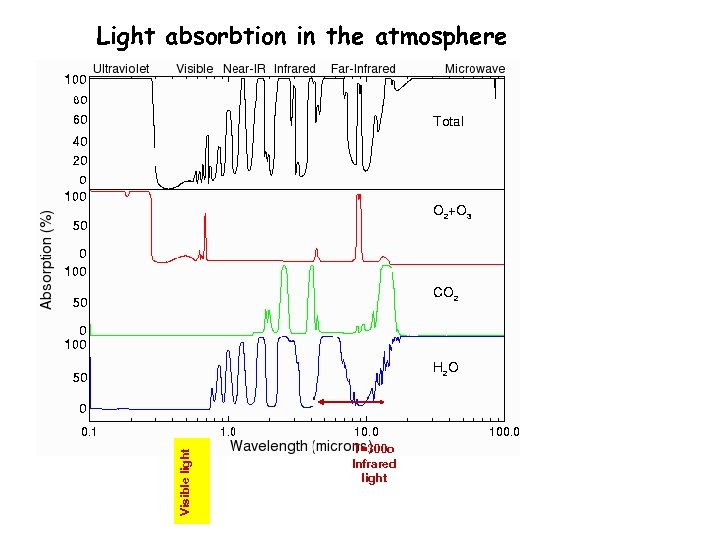
Visible light Light absorbtion in the atmosphere T=300 o Infrared light

Back to Planck, etc…
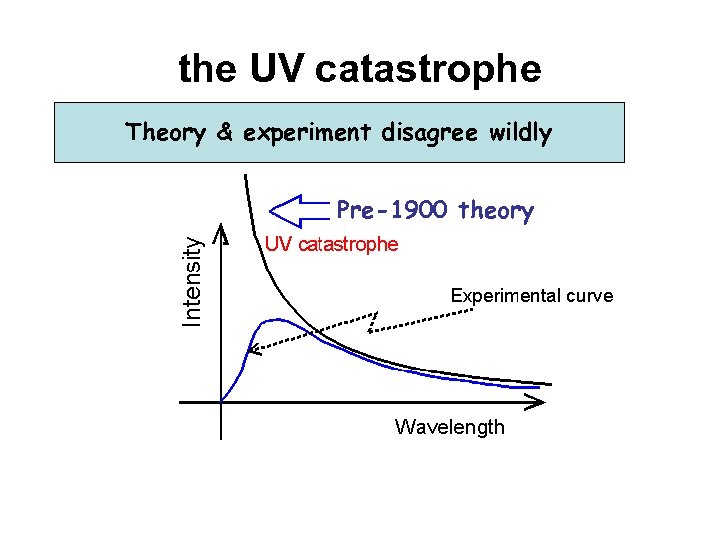
the UV catastrophe Theory & experiment disagree wildly Pre-1900 theory

Planck’s solution EM energy cannot be radiated or absorbed in any arbitrary amounts, but only in discrete “quantum” amounts. The energy of a “quantum” depends on frequency as Equantum = h f h = 6. 6 x 10 -34 Js “Planck’s constant”

Other “quantum” systems

The quantum of the US monetary system We don’t worry about effects of quantization Because the penny’s value is so small (~10와)

Suppose the quantum were a $1000 bill A quantum this large would have an enormous effect on “normal” transactions

The quantum of the US Income tax system
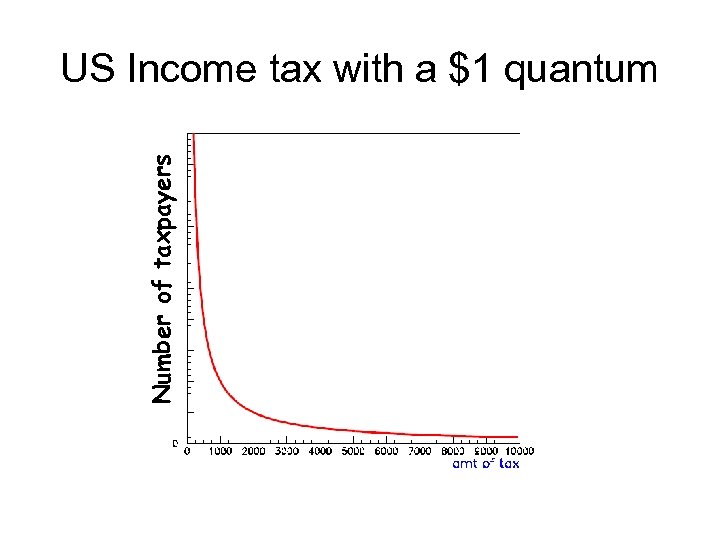
Number of taxpayers US Income tax with a $1 quantum
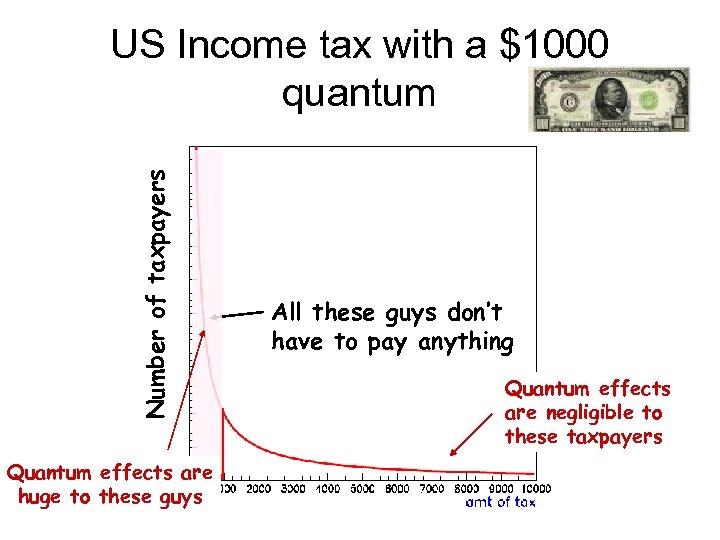
Number of taxpayers US Income tax with a $1000 quantum Quantum effects are huge to these guys All these guys don’t have to pay anything Quantum effects are negligible to these taxpayers
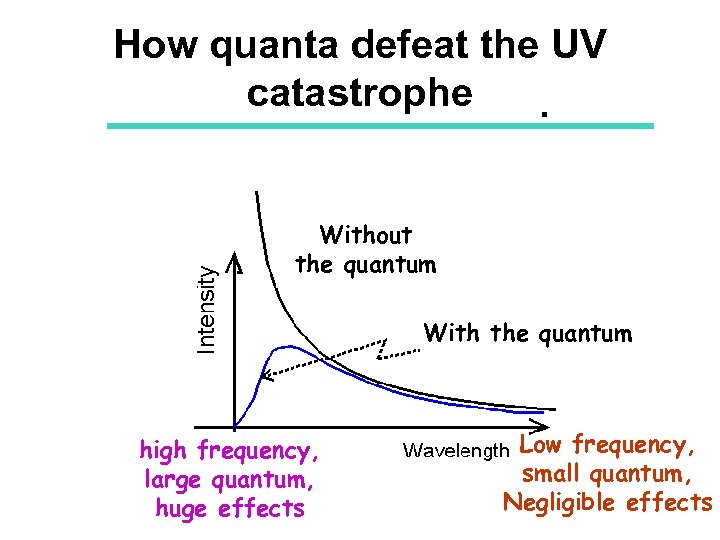
How quanta defeat the UV catastrophe Without the quantum With the quantum high frequency, large quantum, huge effects Low frequency, small quantum, Negligible effects
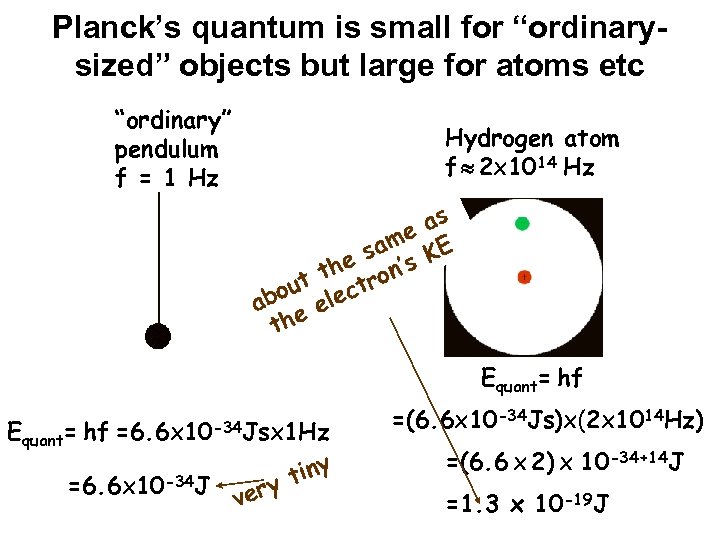
Planck’s quantum is small for “ordinarysized” objects but large for atoms etc “ordinary” pendulum f = 1 Hz Hydrogen atom f 2 x 1014 Hz e am e s n’s th ro out lect ab ee th as KE Equant= hf =6. 6 x 10 -34 Jsx 1 Hz =6. 6 x 10 -34 J y ver tiny =(6. 6 x 10 -34 Js)x(2 x 1014 Hz) =(6. 6 x 2) x 10 -34+14 J =1. 3 x 10 -19 J

Typical energies in “ordinary” life Typical energy of a tot on a swing: Etot = mghmax 20 kgx ==20 kgx 10 m/s 22 x = 20 kgx 10 m/s x 1 m = 200 kgm 2/s 2 = 200 J hmax much, much larger than Equant=6. 6 x 10 -34 J
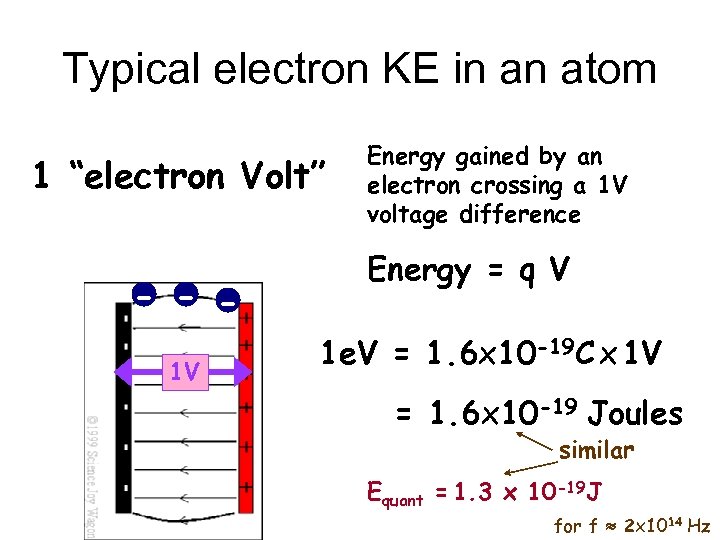
Typical electron KE in an atom 1 “electron Volt” - - 1 V Energy gained by an electron crossing a 1 V voltage difference Energy = q V 1 e. V = 1. 6 x 10 -19 C x 1 V = 1. 6 x 10 -19 Joules similar Equant = 1. 3 x 10 -19 J for f 2 x 1014 Hz

Classical vs Quantum world In everyday life, quantum effects can be safely ignored This is because Planck’s constant is so small At atomic & subatomic scales, quantum effects are dominant & must be considered Laws of nature developed without consideration of quantum effects do not work for atoms

photons “Quantum Jump”
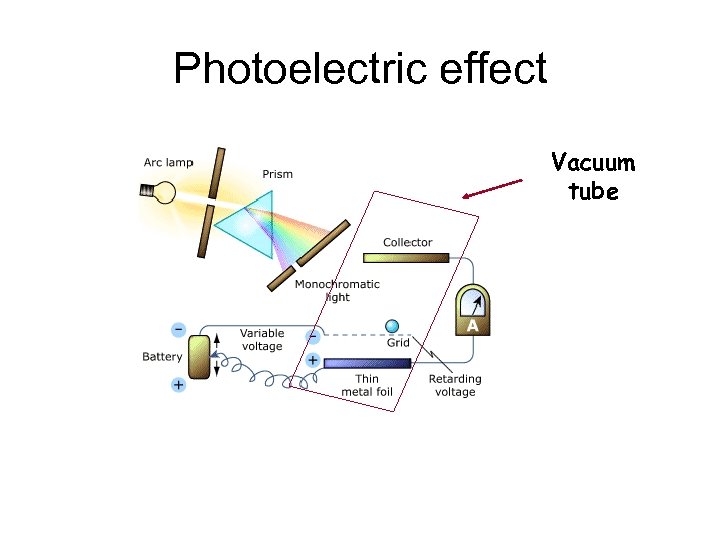
Photoelectric effect Vacuum tube
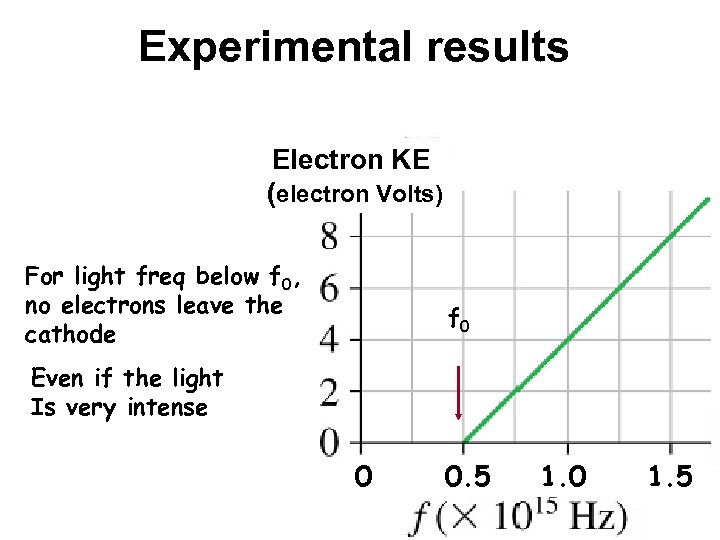
Experimental results Electron KE (electron Volts) For light freq below f 0, no electrons leave the cathode f 0 Even if the light Is very intense 0 0. 5 1. 0 1. 5
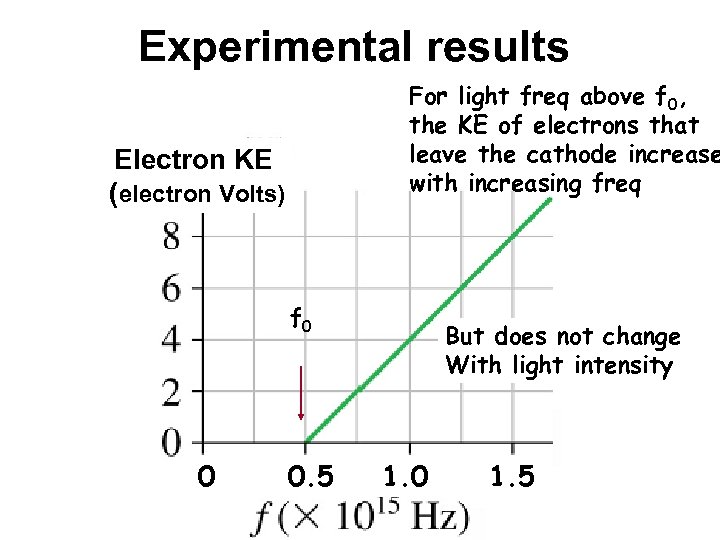
Experimental results For light freq above f 0, the KE of electrons that leave the cathode increase with increasing freq Electron KE (electron Volts) f 0 0 0. 5 But does not change With light intensity 1. 0 1. 5
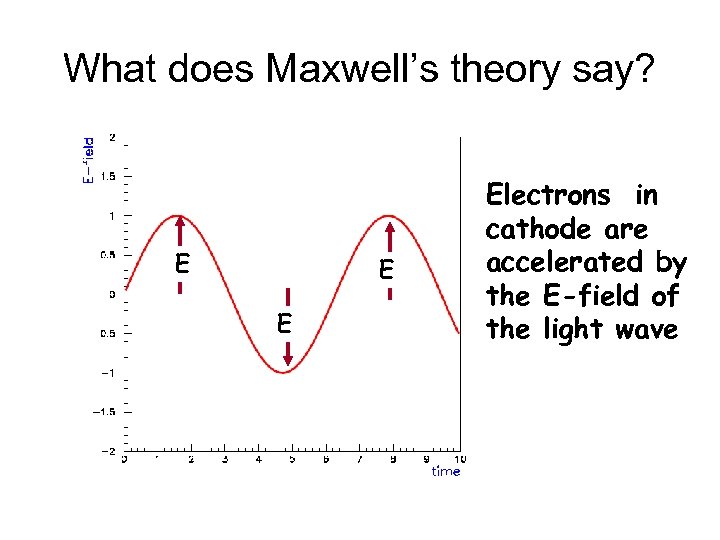
What does Maxwell’s theory say? E Electrons in cathode are accelerated by the E-field of the light wave
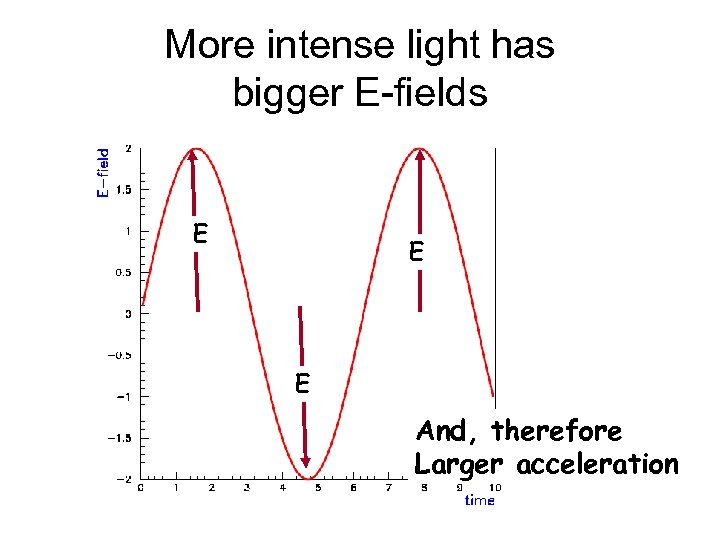
More intense light has bigger E-fields E E E And, therefore Larger acceleration

Electron KE should depend on E-field strength light intensity Electron’s motion s ob s ti ha tw No d rve e
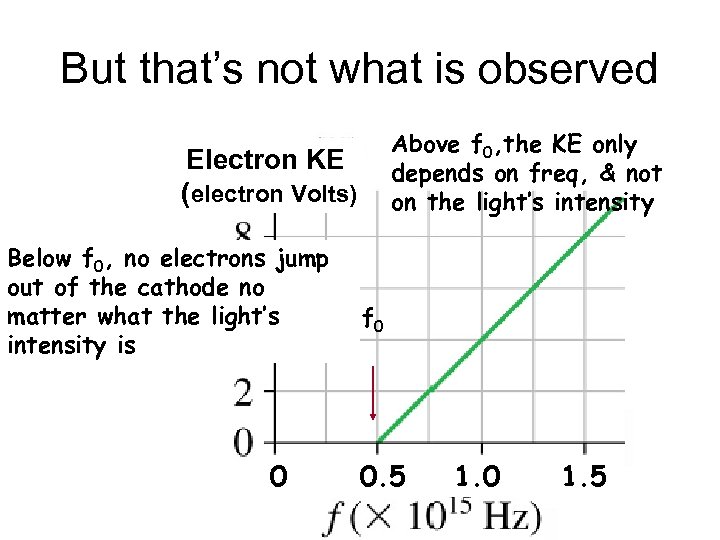
But that’s not what is observed Above f 0, the KE only depends on freq, & not on the light’s intensity Electron KE (electron Volts) Below f 0, no electrons jump out of the cathode no matter what the light’s intensity is 0 f 0 0. 5 1. 0 1. 5
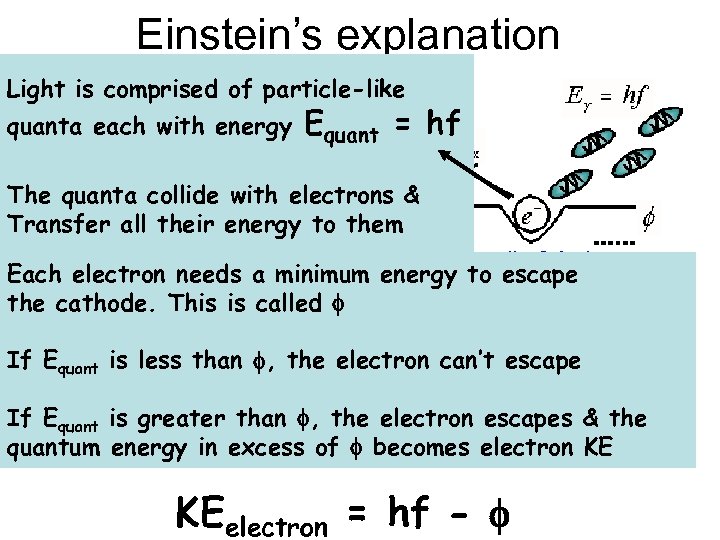
Einstein’s explanation Light is comprised of particle-like quanta each with energy Equant = hf The quanta collide with electrons & Transfer all their energy to them Each electron needs a minimum energy to escape the cathode. This is called f If Equant is less than f, the electron can’t escape If Equant is greater than f, the electron escapes & the f quantum energy in excess of f becomes electron KE KEelectron = hf - f

Light quanta “photons” Einstein’s light quanta were given the name “photons” by Arthur Compton

Photon Energy for red light Red light: f = 4. 0 x 1014 Hz (Hz = 1/s) Ephoton = hf = (6. 6 x 10 -34 Js) x (4. 0 x 1014 Hz) = 2. 6 x 10 -19 J = 2. 6 e. V 1. 6 x 10 -19 J =1. 6 e. V

Photon Energies for visible light color: Red Yellow Green Blue Violet freq 4. 0 x 1014 Hz 5. 0 x 1014 Hz 6. 0 x 1014 Hz 6. 7 x 1014 Hz 7. 5 x 1014 Hz Equant = hf 2. 6 x 10 -19 J 3. 3 x 10 -19 J 4. 0 x 10 -19 J 4. 4 x 10 -19 J 5. 0 x 10 -19 J 1. 6 e. V 2. 1 e. V 2. 5 e. V 2. 8 e. V 3. 1 e. V
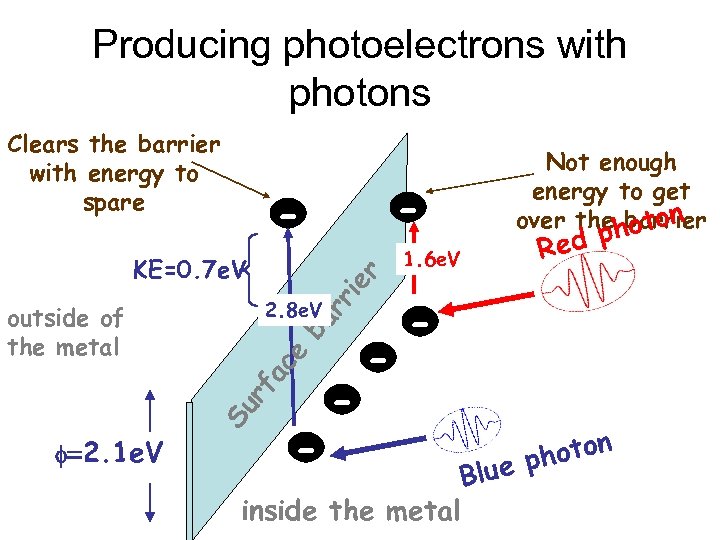
Producing photoelectrons with photons Clears the barrier with energy to spare rr ie r KE=0. 7 e. V ce ba 2. 8 e. V Su rf a outside of the metal - - f=2. 1 e. V - - - 1. 6 e. V Not enough energy to get over thehoton barrier ed p R - inside the metal o phot Blue n
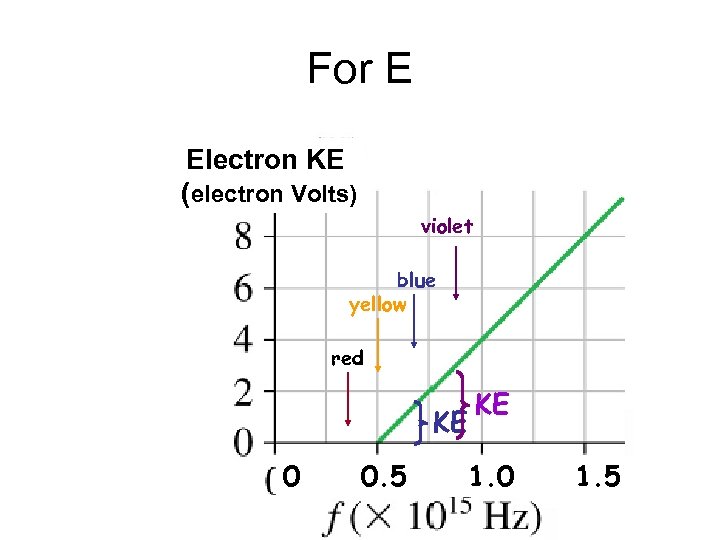
For E Electron KE (electron Volts) violet blue yellow red KE 0 0. 5 KE 1. 0 1. 5

Photons are weird particles v=c (always) g= 1 1 – v 2/c 2 = 1 1 – 1 1 1 – c 2/c 2 = = (always)

What is the photon’s rest mass? E=mc 2 m = g m 0 = 0 E c 2 m= m g = m =0 Rest mass = 0

Photon’s momentum For any particle: p=mv for a photon: m= E 2 c p = E 2 c c & v=c E = c
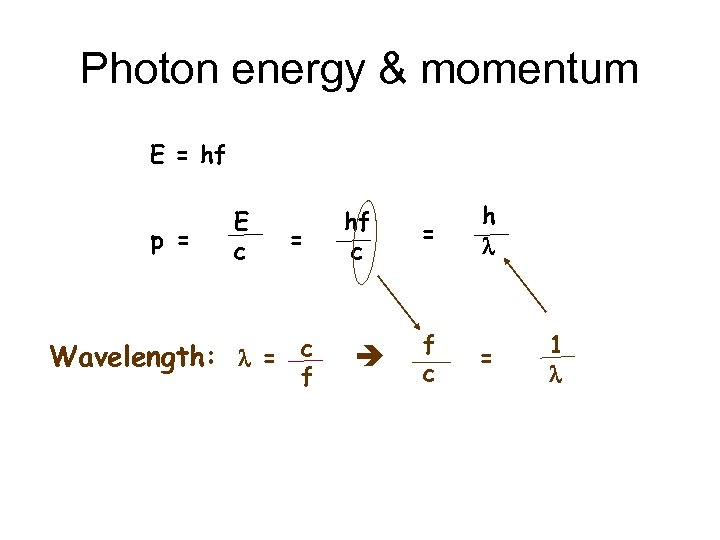
Photon energy & momentum E = hf p = E c = Wavelength: l = c f hf c = h l f c = 1 l
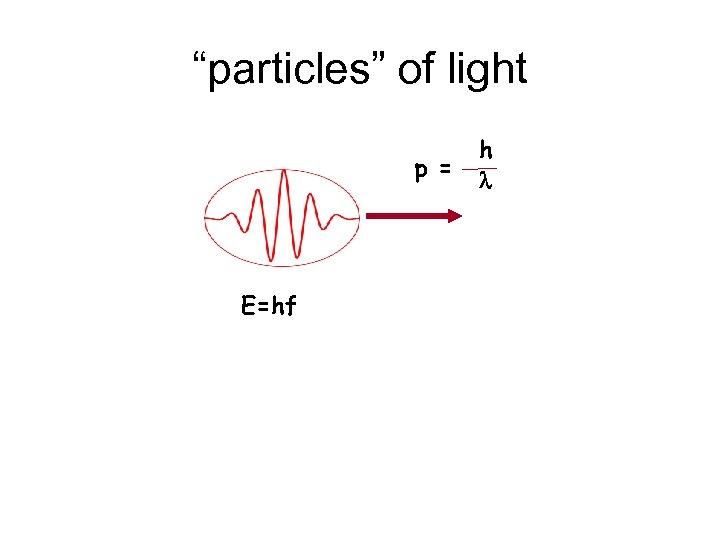
“particles” of light p = E=hf h l
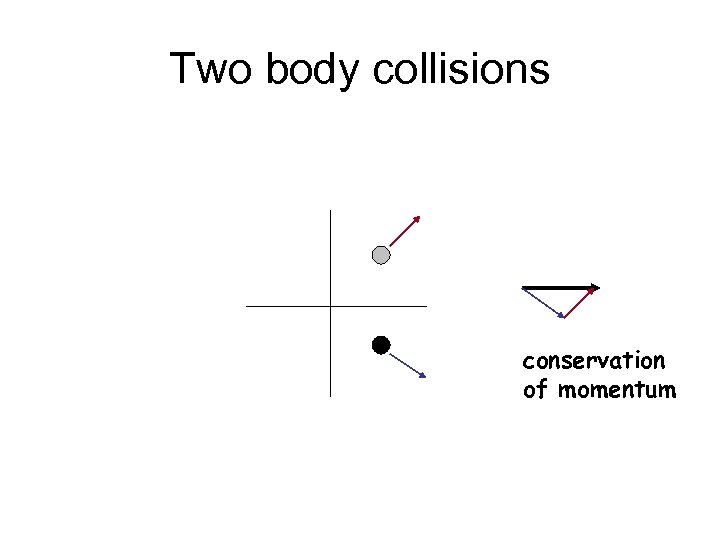
Two body collisions conservation of momentum

Compton scattering Scatter X-rays from electrons p=h/li - p= h/ l f Recoil electron & scattered photon conserve momentum

Compton’s expt proved the existence of photons & won him the 1927 Nobel Prize (Physics)

4 x 10 -11 e. V g-rays X-rays Ultraviolet Infrared micro waves TV/FM AM radio waves Photon “spectrum” 4 x 10 -7 e. V 4 x 10 -3 e. V 4 x 103 e. V visible light 1. 6 – 3. 1 e. V 4 x 106 e. V

Wave? Particles? ?
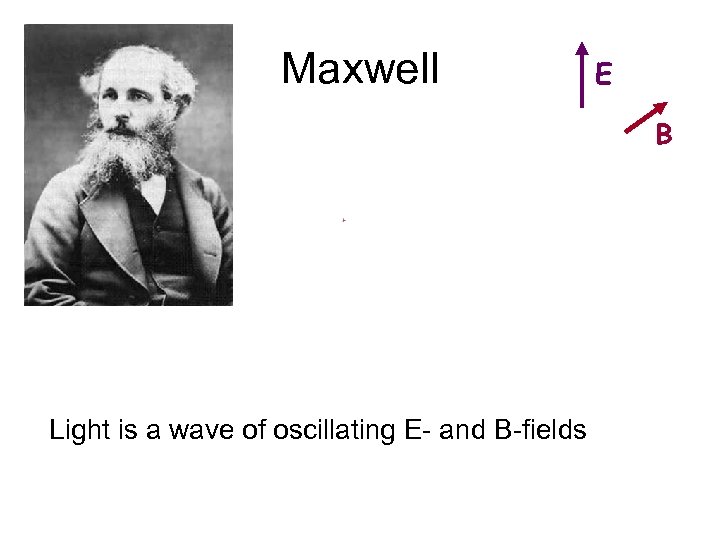
Maxwell E B James Clerk Maxwell Light is a wave of oscillating E- and B-fields

Einstein p = h l E=hf Light is comprised of particle-like quanta called photons

Who’s right? ? Waves explain diffraction & interference Photons explain photoelectric effect & Compton scattering
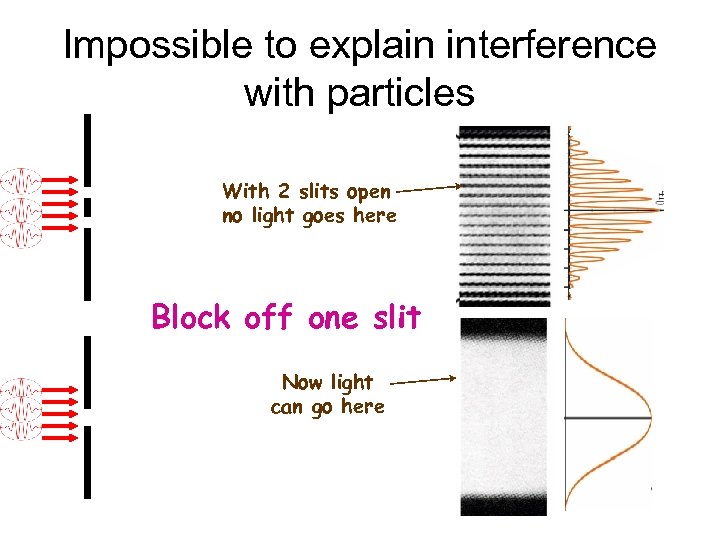
Impossible to explain interference with particles With 2 slits open no light goes here Block off one slit Now light can go here
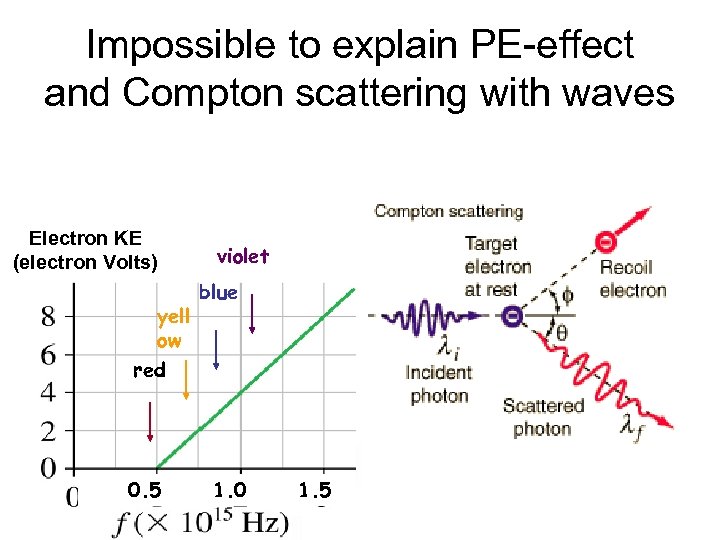
Impossible to explain PE-effect and Compton scattering with waves Electron KE (electron Volts) yell ow violet blue red 0. 5 1. 0 1. 5

Make an interference pattern with low intensity light One photon at a time goes through the two-slit apparatus

-Light behaves like a wave when it propagates through space -And as a particle when it interacts with matter

Photon photography



252f4082c4b3eb1495dcef483add4b92.ppt