БИОИНФОРМАТИКА Карпов Павел Андреевич Лекция 3

БИОИНФОРМАТИКА Карпов Павел Андреевич Лекция № 3

Множественное выравнивание последовательностей • Множественное выравнивание последовательностей (multiple sequence alignment) это выравнение трех и более билолгических последовательностей, обычно белков, ДНК, или РНК. • По сути является попарным выравниваем всех последовательностей в неком наборе и нахождение наиболее «оптимального» общего выравнивания. • Применяется преимущественно для нахождения консервативных участков (мотивов) в наборе последовательностей. • Используется в процессах установления эволюционных связей путем построения филогенетических деревьев. Так как множественное выравниваение является NP-полной задачей, различные ее решения базируются на эвристиках, генетических и иных алгоритмах комбинаторной оптимизации.

Фрагмент множественного выравнивания аминокислотных последовательностей в программе Bio. Edit

Попарное (парное) выравнивание Парное выравнивание последовательностей каталитического комплекса Bub 1 C (каталитический домен и прилегающая к нему N–концевая пристройка) [Kang et al. , 2008] протеинкиназы Bub 1 (Uni. Prot: O 43683; BUB 1_HUMAN) из Homo sapiens и последовательности соответствующей растительным гомологам из риса: EEC 82122. 1 - белок с неизвестной функцией из Oryza sativa Indica и EEE 67244. 1 - белок с неизвестной функцией из Oryza sativa Japonica). Примечание: ##### - нуклеотид (АТФ) -связывающая область (BUB 1_HUMAN: 793 -801); $ - активный сайт (BUB 1_HUMAN: D 917); ¥ - сайт связывания АТФ (BUB 1_HUMAN: K 821)

Парное выравнивание • Парное выравнивание используется для нахождения совпадающих участков двух последовательностей. Различают глобальное и локальное выравнивание. • Глобальное выравнивание применяется к «похожим» последовательностям приблизительно одинаковой длины и наглядно показывает разницу между этими последовательностями. Глобальное: SQ 1: FTFTALILLAVAV SQ 2: F--TAL-LLA-AV • Локальное выравнивание применяется для преимущественно отличающихся друг от друга последовательностей, которые предположительно могут содержат одинаковые участки. Локальное: SQ 1: FTFTALILL-AVAV SQ 2: --FTAL-LLAAV--

Clustal. W и Clustal. X • Clustal. W — Программа для множественного выравнивания последовательностей ДНК и белков. Работает в два этапа. • Первый — попарное выравнивание всех со всеми для оценки сходства. • Второй этап — после построения филогенетического дерева выравнивание глобальное. • В отличие от программы Clustal. X, использующей графический интерфейс, Clustal. W работает через командную строку или он-лайн.

EBI web server http: //www. ebi. ac. uk/Tools/msa/clustalw 2/

Swiss Institute of Bioinformatics http: //www. ch. embnet. org/software/Clustal. W. html

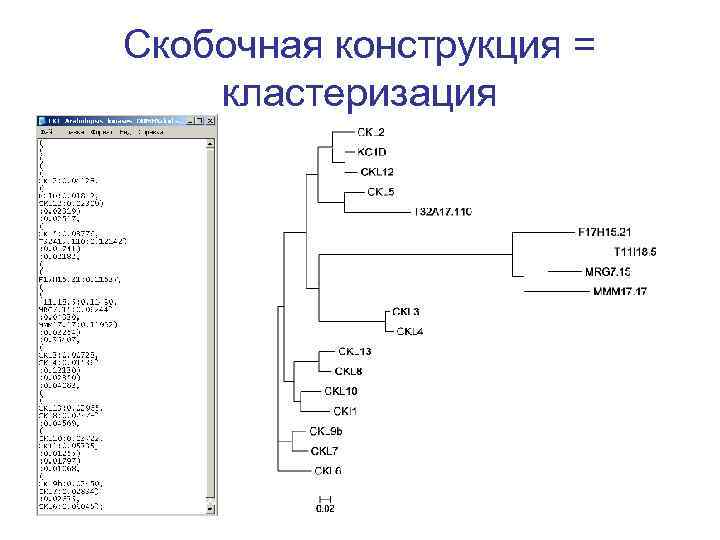
Скобочная конструкция = кластеризация

MUSCLE - Multiple Sequence Alignment http: //www. ebi. ac. uk/Tools/msa/muscle/

T-Coffee

МАТРИЦЫ ЗАМЕН АМИНОКИСЛОТ • GONNET (Gonnet et al. , 1992) • PAM (Point Accepted Mutation) (Dayhoff et al. , 1978) • BLOSUM (BLOcks SUbstitution Matrix) (Henikoff, 1992)

Матрицы PAM (Point Accepted Mutation) • Матрицы PAM вычислены путем анализа • выравнивании очень сходных белков, единица PAM - вероятность замены одной • аминокислоты на другую в период, в который фиксируется 1 мутация аминокислоты на • 100 аминокислот. Наиболее используемая матрица PAM 250, например, отражает • стоимость подобия между последовательностями с 20%-ной степенью гомологии. • Dayhoff, M. O. , Schwartz, R. M. , Orcutt, B. C. ( 1978) A model of evolutionary change in proteins. In "Atlas of Protein Sequence and Structure" 5(3) M. O. Dayhoff (ed. ), 345 - 352.

PAM 250 PAM (Point Accepted Mutation) matrices were proposed by Dayhoff et al in 1978 based on observations of alignments of closely related proteins. The frequencies of substitution of each pair of amino acids were extracted from alignments of proteins of small evolutionary distance, below 1% divergence. PAM matrices are based on mutations observed throughout a global alignment, this includes both highly conserved and highly mutable regions. The PAM 250 matrix is appropriate for searching for alignments of sequences that have diverged by 250 PAMs, 250 mutations per 100 amino acids of sequence. Because of back mutations and silent mutations this corresponds to sequences that are about 20 percent identical.

Матрицы BLOSUM (Blocks Substitution Matrix) • Матрицы BLOSUM вычислены путем анализа выровненных лишенных делеций сегментов • последовательностей, единица BLOSUM - логарифм отношения шансов встречи • определенной пары аминокислот во множественном выравнивании. Наиболее • используемая матрица BLOSUM 62 отражает логарифм отношения шансов встречи • определенной пары аминокислот в последовательностях с 62%-ной степенью сходстав. • Henikoff, S. and Henikoff, J. (1992) Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA. 89(biochemistry): 10915 - 10919. 1992.

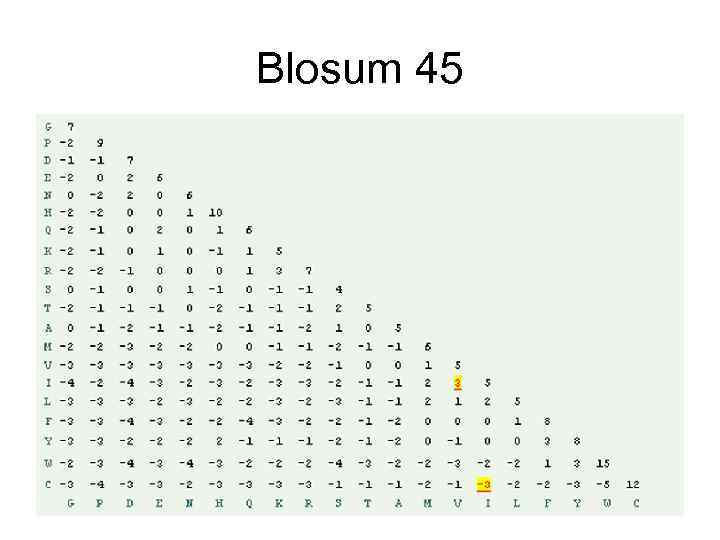
Blosum 45

Blosum 62 BLOSUM (Blocks Substitution Matrix) matrices are based on local alignments. BLOSUM 62 is a matrix calculated from comparison of sequences with no more than 62% divergence. BLOSUM 62 is the default matrix in BLAST 2. 0 and it performs well in detecting closer relationships. BLOSUM 62 is a scoring matrix where every possible identity and substitution is assigned a score based on the observed frequencies of such occurences in alignments of related proteins. -Identities are assigned the most positive scores. -Frecuently observed substitutions receive positive scores. -Seldom observed substitutions are given negative scores.

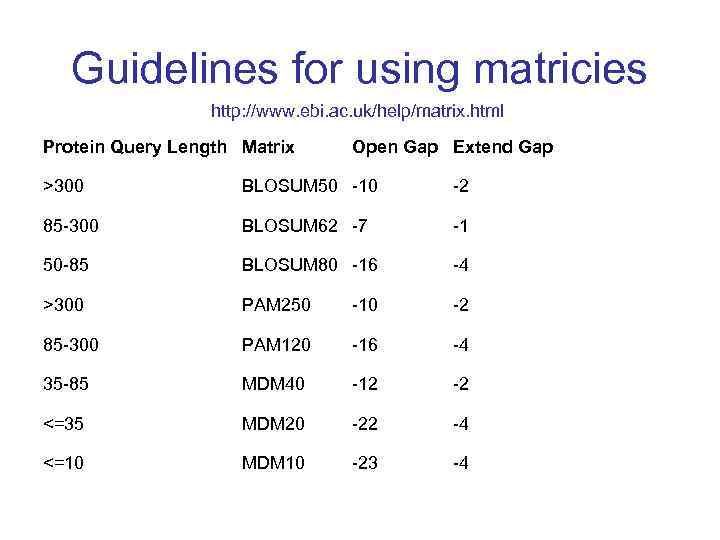
Guidelines for using matricies http: //www. ebi. ac. uk/help/matrix. html Protein Query Length Matrix Open Gap Extend Gap >300 BLOSUM 50 -10 -2 85 -300 BLOSUM 62 -7 -1 50 -85 BLOSUM 80 -16 -4 >300 PAM 250 -10 -2 85 -300 PAM 120 -16 -4 35 -85 MDM 40 -12 -2 <=35 MDM 20 -22 -4 <=10 MDM 10 -23 -4

Соответствие матриц PAM и Blosum • • • PAM 100 ==> Blosum 90 PAM 120 ==> Blosum 80 PAM 160 ==> Blosum 60 PAM 200 ==> Blosum 52 PAM 250 ==> Blosum 45

Матрицы GONNET • GONNET базируются на дистанциях PAM, единица этих матриц – десятикратный логарифм отношения вероятностей закономерного и случайного выравнивания аминокислот. Нововведение матриц GONNET – стандартизованная оценка значений штрафов на делецию определенных аминокислот. • Gonnet G. H. , Cohen M. A. , Benner S. A. (1992). Exhaustive matching of the entire protein sequence database. Science 1992 Jun 5; 256(5062): 1443 -5.

The GONNET matrix was proposed by Gonnet, Cohen and Benner (1992). The Gonnet matrix is a scoring matrix based on the alignment of the entire SWISS-PROT database. They used classical distance measures to estimate an alignment of the proteins. They then used this data to estimate a new distance matrix. This was used to refine the alignment, estimate a new distance matrix and so on iteratively.

Матрицы DNA • IUB - это весовая матрица разработанная для сравнения нуклеотидных последовательностей в программе BESTFIT (использует алгоритм Смита. Ватермана для поиска лучшего локального выравнивания 2 -х последовательностей). В IUB символы ‘X’ и ‘N’ трактуются как совпадения или не совпадения символов. Вес всех совпадений = 1. 9; вес всех не совпадений = 0. • CLUSTALW. Совпадения имеют вес = 1. 0, а все несовпадения = 0.

Построение множественных выравниваний и их анализ Развитие представлений об эволюции белков Создание коллекций мотивов в аминокислотных последовательностях

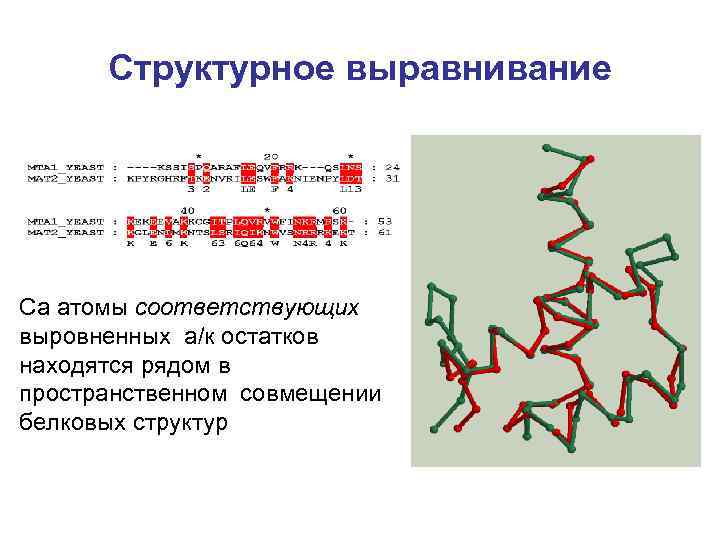
Структурное выравнивание Сa атомы соответствующих выровненных а/к остатков находятся рядом в пространственном совмещении белковых структур

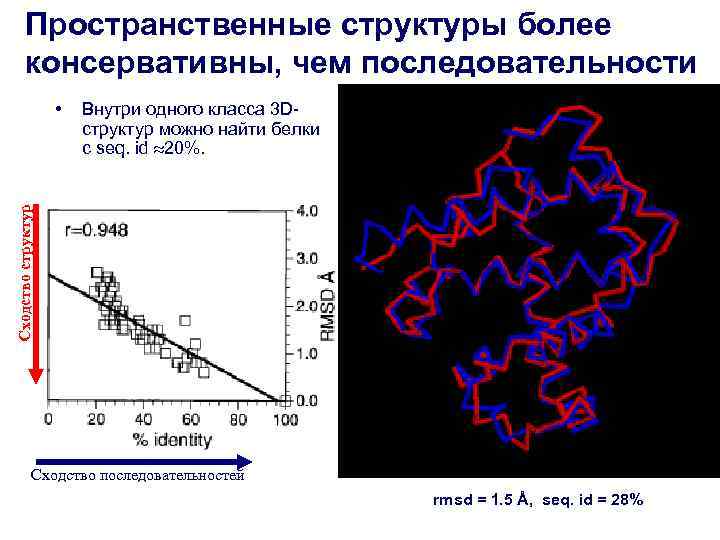
Пространственные структуры более консервативны, чем последовательности • Внутри одного класса 3 D- структур можно найти белки с seq. id 20%. Сходство структур Сходство последовательностей rmsd = 1. 5 Å, seq. id = 28%

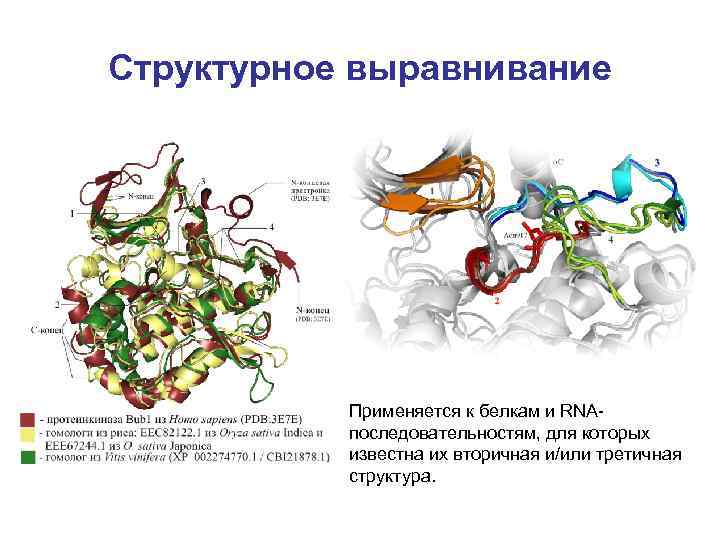
Структурное выравнивание Применяется к белкам и RNAпоследовательностям, для которых известна их вторичная и/или третичная структура.

Семейства белков Паттерны и профили

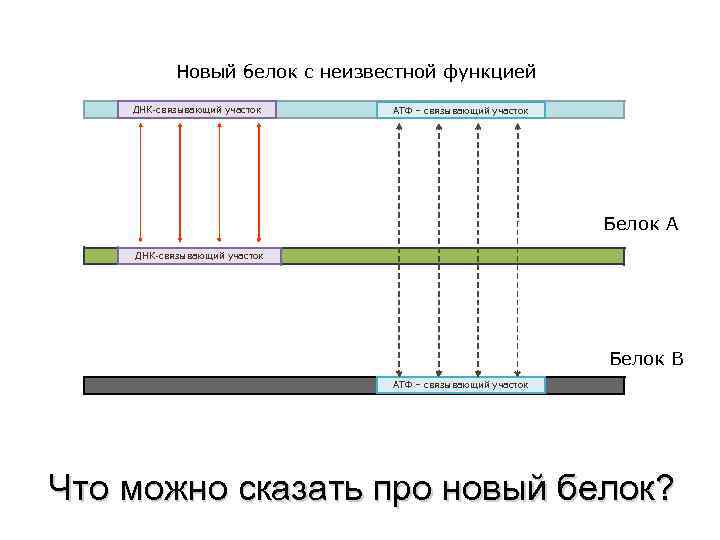
Новый белок с неизвестной функцией ДНК-связывающий участок АТФ – связывающий участок Белок А ДНК-связывающий участок Белок В АТФ – связывающий участок Что можно сказать про новый белок?

Мотив ? • Мотив в аминокислотной последовательности - набор консервативных остатков, важных для функции белка и расположенных на определенном (обычно коротком) расстоянии друг от друга в последовательности. • Мотив структуры (структурный мотив) – часто встречающийся в белках элемент пространственной структуры ( спираль, -шпилька, -поворот). В общем случае, структурные мотивы не обязательно соответствуют мотивам в аминокислотным последовательностях. Один домен может содержать один или несколько мотивов в аминокислотной последовательности. Мотив может не входить в домены. Не в любом выравнивании легко найти мотив.

Домен – единица эволюции, структуры и функции белков. Домен – компактная, относительно независимо сворачивающаяся структура, относительно консервативная в процессе эволюции. Белки могут состоять из одного или многих доменов. nitrogen fixation positive activator protein

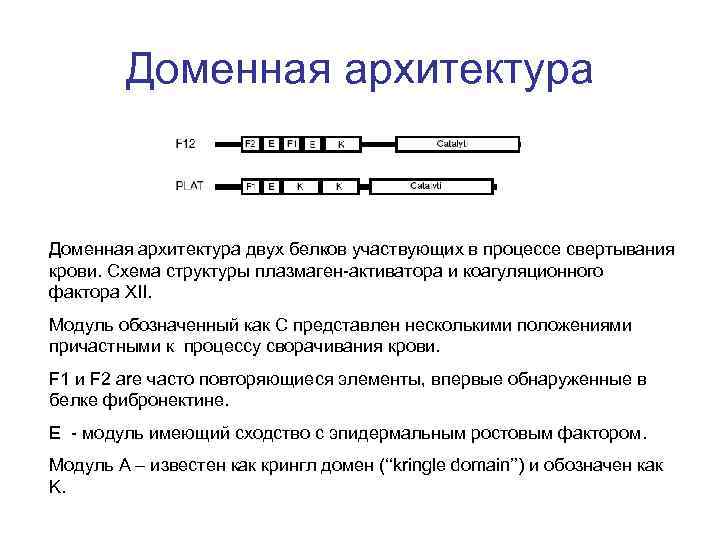
Доменная архитектура двух белков участвующих в процессе свертывания крови. Схема структуры плазмаген-активатора и коагуляционного фактора XII. Модуль обозначенный как С представлен несколькими положениями причастными к процессу сворачивания крови. F 1 и F 2 are часто повторяющиеся элементы, впервые обнаруженные в белке фибронектине. E - модуль имеющий сходство с эпидермальным ростовым фактором. Модуль A – известен как крингл домен (‘‘kringle domain’’) и обозначен как K.

Семейство - группа белков, имеющая общее происхождение. Аминокислотные последовательности выравниваются по всей длине со значимым весом и имеют сходную доменную структуру. Мнения расходятся, когда речь идет о критериях: насколько должны быть похожи белки одного семейства (id>=30%, id>= 50%) ? ? ? должны белки одного семейства иметь в точности одну и ту же доменную структуру? Superfamily Family Subfamily Не корректнее ли говорить о семействах доменов?

Основные понятия и термины • Место, сайт (site) • Мотив (motif) – • Домен (domain) – • Семейство – • Суперсемейство - ? • Паттерн (pattern) – • Позиционно специфическая матрица весов (PSSM) – • Профиль–HМM • Подпись (signature) – • «Oтпечатки пальцев» (fingerprints) – • Кластер -

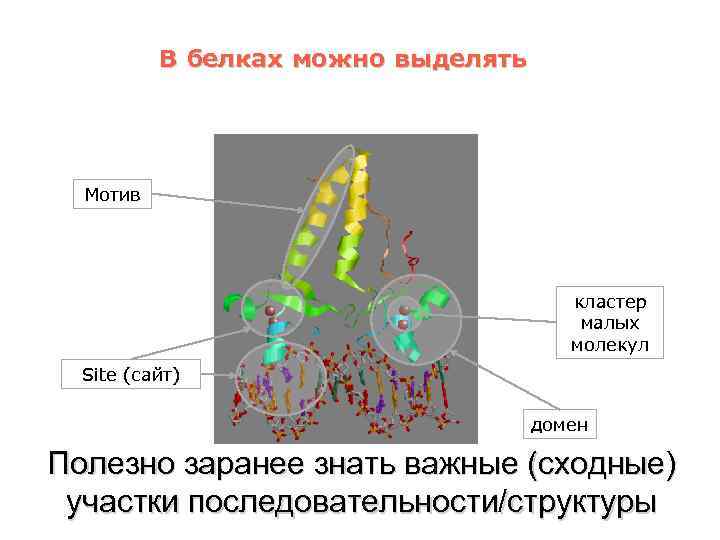
В белках можно выделять Мотив кластер малых молекул Site (сайт) домен Полезно заранее знать важные (сходные) участки последовательности/структуры

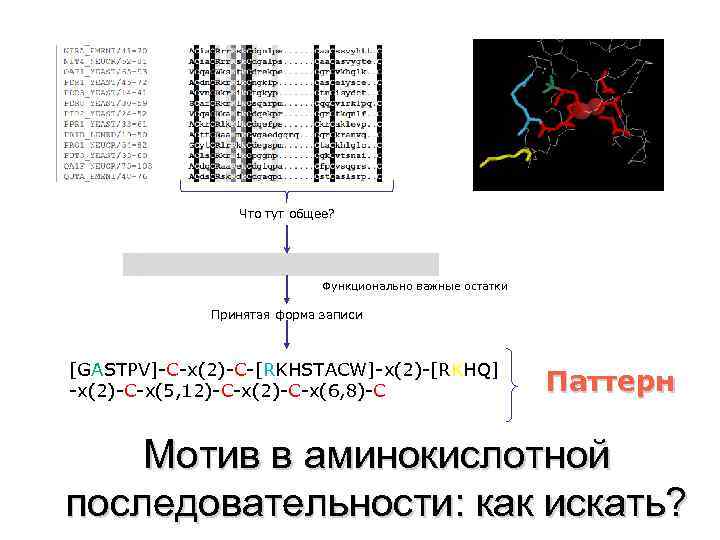
Что тут общее? ? С? ? СR? ? K? ? C? ? ? C Функционально важные остатки Принятая форма записи [GASTPV]-C-x(2)-C-[RKHSTACW]-x(2)-[RKHQ] -x(2)-C-x(5, 12)-C-x(6, 8)-C Паттерн Мотив в аминокислотной последовательности: как искать?

Пример простого мотива Алкогольдегидрогеназа 6 (человек) 68 - 82: GHEg. AGIvesi. Geg. V Алкогольдегидрогеназа класса 3 (рис) 70 - 84: GHEa. AGIvesv. Geg. V Алкогольдегидрогеназа, специфичная к пропанолу (кишечная палочка) 57 - 71: GHEg. IGVvaev. Gpg. V Распознающее правило типа «паттерн» : G - H - E - x - {EL} - G - {AP} - x(4) - [GA] - x(2) - [IVSAC] Паттерн – регулярное выражение UNIX’a: Например, выражение [AC]-x-V-x(4)-{ED} читается как Ala или Cys- х-Val- х- х- х - х- (любой остаток, но не Glu и не Asp)

Выравнивание хорошо изученного семейства Функционально важные остатки 4 -5 консервативных остатков x [AT] {CR} K(3) X(2, 4) < > любая а/к Ala или Thr кроме Cys и Arg K-K-K x-x или x-x-x-x / A(2, 4) N- конец C- конец Паттерн Поиск в Uni. Prot Если много лишнего, то увеличиваем паттерн [AC]-x-V-x(4)-{ED} Если находим только «правильные» , то ОК Как создать паттерн?

БД белковых доменов, семейств и функциональных сайтов Содержит описание объектов + описание паттернов, профилей и правил для их обнаружения. Релиз 20. 47 14 -Apr-2009 1547 документов, 1308 паттернов, 845 профилей + 846 Pro. Rule PROSITE ─ биологически значимые сайты, паттерны и профили, http: //www. expasy. ch/prosite/

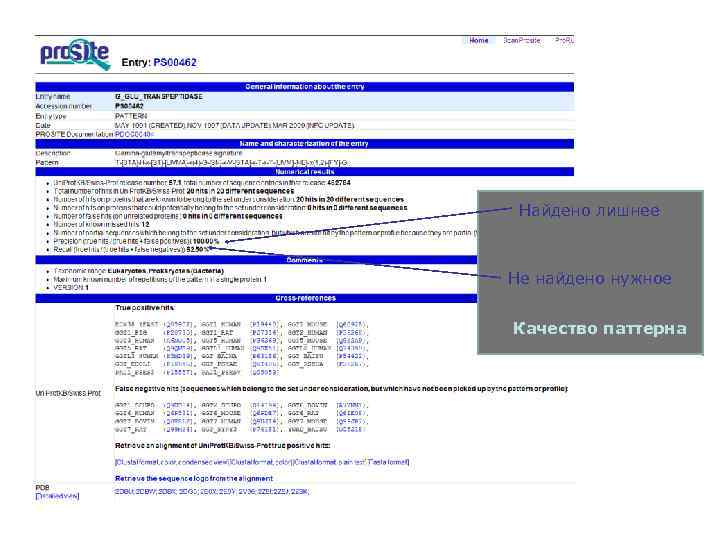
Найдено лишнее Не найдено нужное Качество паттерна

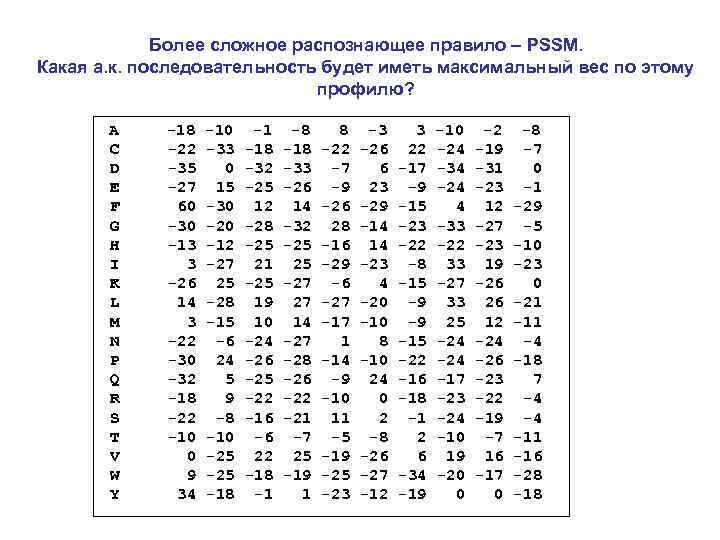
Более сложное распознающее правило – PSSM. Какая а. к. последовательность будет иметь максимальный вес по этому профилю? A C D E F G H I K L M N P Q R S T V W Y -18 -22 -35 -27 60 -30 -13 3 -26 14 3 -22 -30 -32 -18 -22 -10 0 9 34 -10 -33 0 15 -30 -20 -12 -27 25 -28 -15 -6 24 5 9 -8 -10 -25 -18 -1 -18 -32 -25 12 -28 -25 21 -25 19 10 -24 -26 -25 -22 -16 -6 22 -18 -1 -8 -18 -33 -26 14 -32 -25 25 -27 27 14 -27 -28 -26 -22 -21 -7 25 -19 1 8 -22 -7 -9 -26 28 -16 -29 -6 -27 -17 1 -14 -9 -10 11 -5 -19 -25 -23 -3 -26 6 23 -29 -14 14 -23 4 -20 -10 8 -10 24 0 2 -8 -26 -27 -12 3 22 -17 -9 -15 -23 -22 -8 -15 -9 -9 -15 -22 -16 -18 -1 2 6 -34 -19 -10 -24 -34 -24 4 -33 -22 33 -27 33 25 -24 -17 -23 -24 -10 19 -20 0 -2 -19 -31 -23 12 -27 -23 19 -26 26 12 -24 -26 -23 -22 -19 -7 16 -17 0 -8 -7 0 -1 -29 -5 -10 -23 0 -21 -11 -4 -18 7 -4 -4 -11 -16 -28 -18

Pfam • http: //www. sanger. ac. uk/Software/Pfam/index. shtml • Большая коллекция множественных выравниваний, доменов, семейств и профилей-HMM для них. • Состоит из 2 -х частей: § Pfam. A – курируемая часть, покрывает 74% Uni. Prot § Pfam. B – большое число маленьких семейств из автоматически сгенерированной базы доменов Pro. Dom, не вошедших в Pfam. A. • Удобна для анализа доменной структуры белков.

http: //pfam. sanger. ac. uk/search

http: //smart. embl-heidelberg. de/