Бинарные деревья поиска Кормен, Лейзерсон, Ривест, Штайн. Алгоритмы: построение и анализ. 2 -е изд. Глава 12 Шеремета Ирина
Что такое бинарное дерево поиска? Деревья поиска представляют собой структуры данных, которые поддерживают многие операции с динамическими множествами, включая: ь поиск элемента ь поиск минимального и максимального значения ь поиск предшествующего и последующего значения ь вставку и удаление Свойство бинарного дерева поиска: если x – узел бинарного дерева поиска, а узел y находится в левом поддереве x, то если узел y находится в правом поддереве x, то
Способы обхода дерева ь ь ь Центрированный (симметричный) обход дерева (inorder tree walk) обход в прямом порядке (preorder tree walk) обход обратном порядке (postorder tree walk) Центрированный обход Псевдокод Язык С Inorder_Tree_Walk(x) 1 if 2 then Inorder_Tree_Walk(left[x]) 3 print key[x] 4 Inorder_Tree_Walk(right[x]) void Inorder_Tree_Walk(struct TNode *x) { if (x != NULL) { Inorder_Tree_Walk(x->left); printf("%d ", x->key); Inorder_Tree_Walk(x->right); } } Теорема. Если x – корень поддерева, в котором имеется n узлов, то функция Inorder_Tree_Walk(x) выполняется за время
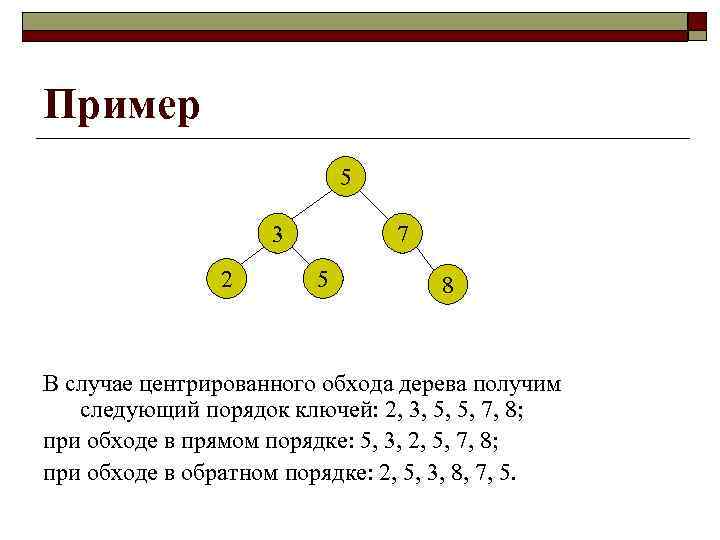
Пример 5 3 2 7 5 8 В случае центрированного обхода дерева получим следующий порядок ключей: 2, 3, 5, 5, 7, 8; при обходе в прямом порядке: 5, 3, 2, 5, 7, 8; при обходе в обратном порядке: 2, 5, 3, 8, 7, 5.
Поиск Алгоритм поиска начинается с корня дерева и проходит вниз по дереву. Для каждого узла x на пути вниз его ключ key[x] сравнивается с переданным в качестве параметра ключом k. Если ключи одинаковы, поиск завершается. Если k меньше key[x], поиск продолжается в левом поддереве x; если больше – то поиск переходит в правое поддерево. Псевдокод Язык С Tree_Search(x, k) struct TNode *Tree_Search(struct TNode *x, int k) { if (x == NULL || k == x->key) return x; if (k < x->key) return Tree_Search(x->left, k); 1 if x = 2 3 if k < 4 then 5 NIL или k = key[x] then return x key[x] return Tree_Search(left[x], k) else return Tree_Search(right[x], k) else return Tree_Search(x->right, k); } Узлы, которые мы посещаем при рекурсивном поиске, образуют нисходящий путь от корня дерева, так что время работы функции Tree_Search равно O(h), где h – высота дерева.
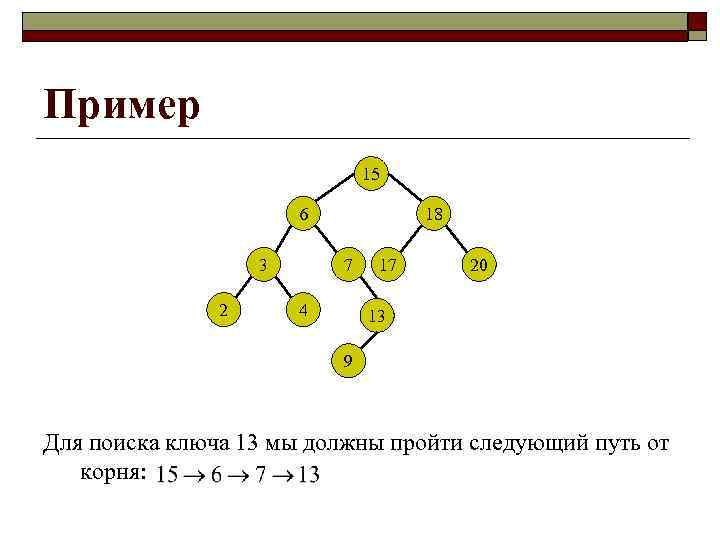
Пример 15 6 3 2 18 7 4 17 20 13 9 Для поиска ключа 13 мы должны пройти следующий путь от корня:
Поиск минимума и максимума Элемент с минимальным (максимальным) значением ключа легко найти, следуя по указателям left (right) от корневого узла до тех пор, пока не встретится значение NIL. Псевдокод Язык С Tree_Minimum(x) 1 while 2 do 3 return x struct TNode *Tree_Minimum(struct TNode *x) { while (x->left != NULL) x = x->left; return x; } Tree_Maximum(x) 1 while 2 do 3 return x struct TNode *Tree_Maximum(struct TNode *x) { while (x->right != NULL) x = x->right; return x; } Обе представленные процедуры находят минимальный (максимальный) элемент за время O(h), где h – высота дерева, поскольку, как и в процедуре Tree_Search, последовательность проверяемых узлов образует нисходящий путь от корня дерева.
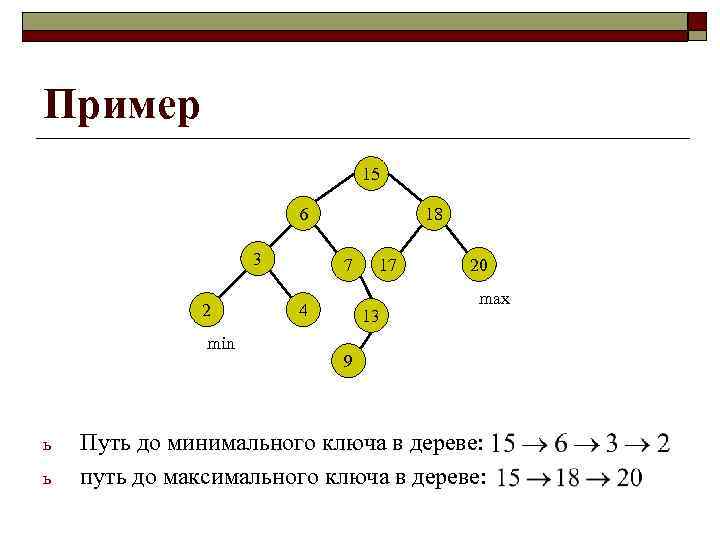
Пример 15 6 3 2 min ь ь 18 7 4 17 13 20 max 9 Путь до минимального ключа в дереве: путь до максимального ключа в дереве:
Предшествующий и последующий элементы Поиск последующего элемента разбивается на 2 части. Если правое (левое) поддерево x непустое, то следующий за x элемент является крайним левым узлом в правом поддереве, который обнаруживается вызовом процедуры Tree_Minimum(right[x]). Если правое поддерево узла x пустое, и у x имеется следующий за ним элемент y, то y является наименьшим предком x, чей левый наследник также является предком x. Для того чтобы найти y, мы просто поднимаемся вверх по дереву до тех пор, пока не встретим узел, который является левым дочерним узлом своего родителя. Время работы алгоритма в дереве высотой h составляет O(h), поскольку мы либо движемся по пути вниз от исходного узла, либо по пути вверх.
![Реализация Предшествующий Последующий Tree_Successor(x) 1 if 2 then return Tree_Minimum(right[x]) 3 4 while и](https://present5.com/presentation/101343894_78123946/image-10.jpg "Реализация Предшествующий Последующий Tree_Successor(x) 1 if 2 then return Tree_Minimum(right[x]) 3 4 while и")
Реализация Предшествующий Последующий Tree_Successor(x) 1 if 2 then return Tree_Minimum(right[x]) 3 4 while и 5 do 6 7 return y Tree_Predecessor(x) 1 if 2 then return Tree_Maximum(left[x]) 3 4 while и 5 do 6 7 return y struct TNode *Tree_Successor(struct TNode *x) { struct TNode *y; if (x->right != NULL) return Tree_Minimum(x->right); y = x->p; while (y != NULL && x == y->right) { x = y; y = y->p; } return y; } struct TNode *Tree_Predecessor(struct TNode *x) { struct TNode *y; if (x->left != NULL) return Tree_Maximum(x->left); y = x->p; while (y != NULL && x == y->left) { x = y; y = y->p; } return y; }
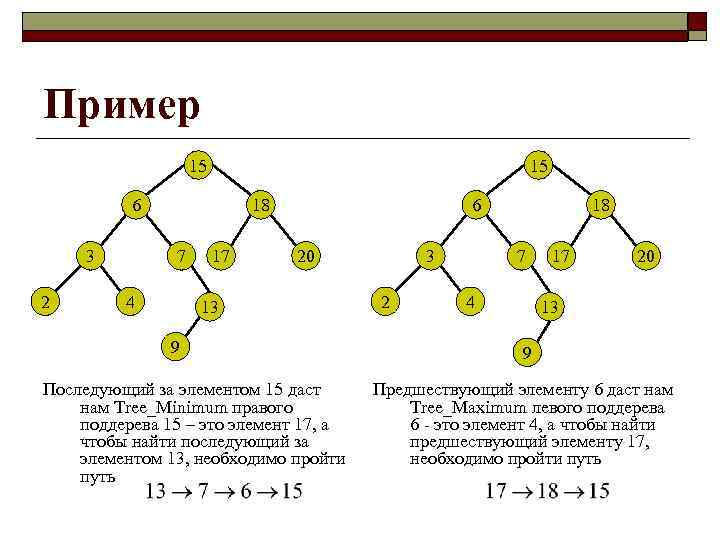
Пример 15 15 6 3 2 18 7 4 17 6 20 13 9 Последующий за элементом 15 даст нам Tree_Minimum правого поддерева 15 – это элемент 17, а чтобы найти последующий за элементом 13, необходимо пройти путь 3 2 18 7 4 17 20 13 9 Предшествующий элементу 6 даст нам Tree_Maximum левого поддерева 6 - это элемент 4, а чтобы найти предшествующий элементу 17, необходимо пройти путь
Вставка Алгоритм вставки элемента в бинарное дерево начинает работу с корневого узла дерева и проходит по нисходящему пути. Указатель x отмечает проходимый путь, а указатель y указывает на родительский по отношению к x узел. В цикле эти указатели перемещаются вниз по дереву влево или вправо в зависимости от результата сравнения ключей key[x] и key[z] до тех пор, пока x не станет равным NIL. Это значение находится именно в той позиции, куда следует поместить z. Время работы: O(h) в дереве высотой h.
Реализация Псевдокод Язык С Tree_Insert(T, z) void Tree_Insert(struct TNode *z) { struct TNode *x, *y; y = NULL; x = root; while (x != NULL) { y = x; if (z->key < x->key) x = x->left; else x = x->right; } z->p = y; if (y == NULL) root = z; else if (z->key < y->key) y->left = z; else y->right = z; } 1 2 3 while 4 do 5 if key[z] < key[x] 6 then 7 else 8 9 10 11 12 13 if y = NIL then else if key[z] < key[y] then else
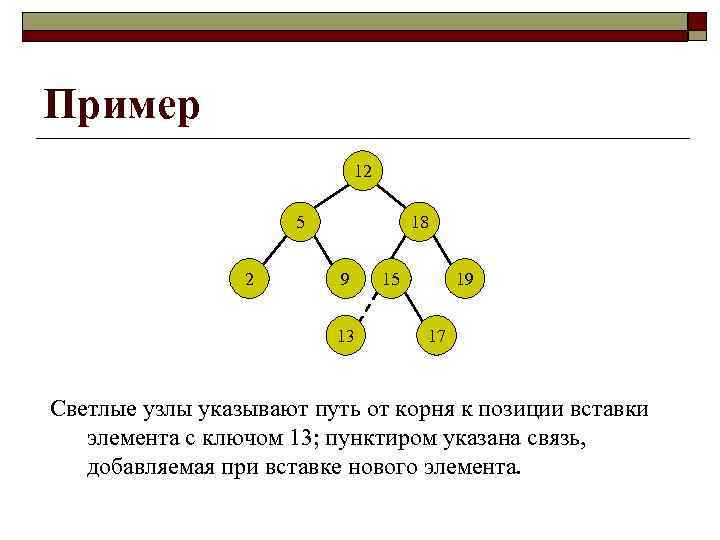
Пример 12 18 5 2 9 13 15 19 17 Светлые узлы указывают путь от корня к позиции вставки элемента с ключом 13; пунктиром указана связь, добавляемая при вставке нового элемента.
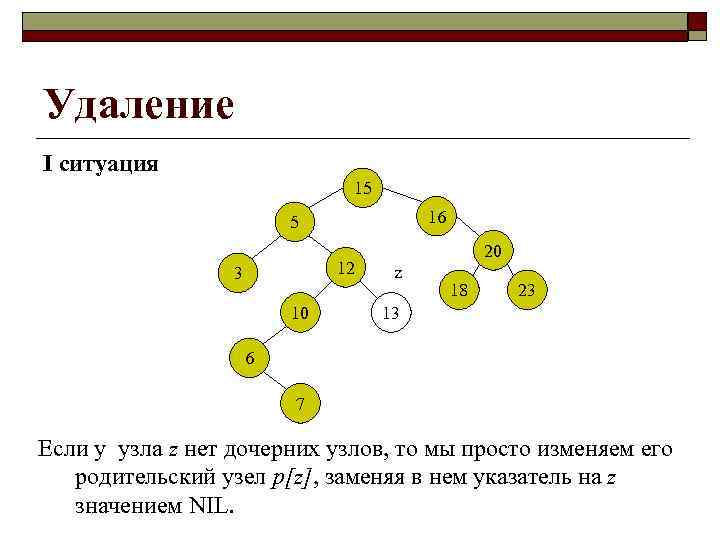
Удаление I ситуация 15 16 5 12 3 10 20 z 18 23 13 6 7 Если у узла z нет дочерних узлов, то мы просто изменяем его родительский узел p[z], заменяя в нем указатель на z значением NIL.
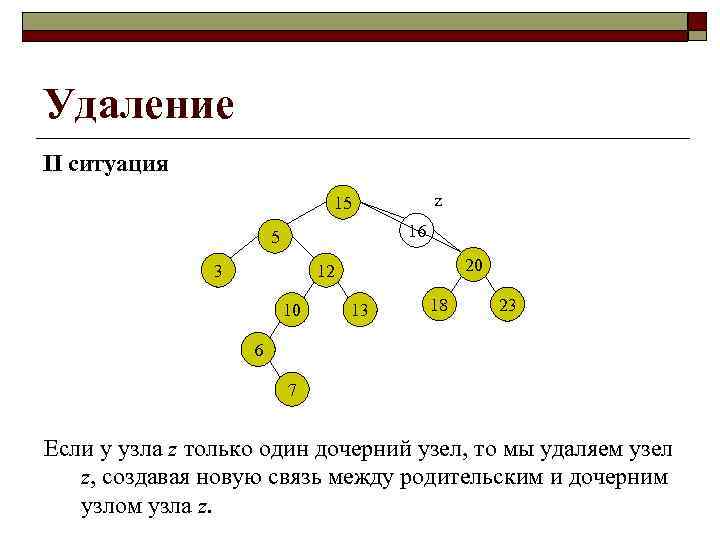
Удаление II ситуация z 15 16 5 3 20 12 10 13 18 23 6 7 Если у узла z только один дочерний узел, то мы удаляем узел z, создавая новую связь между родительским и дочерним узлом узла z.
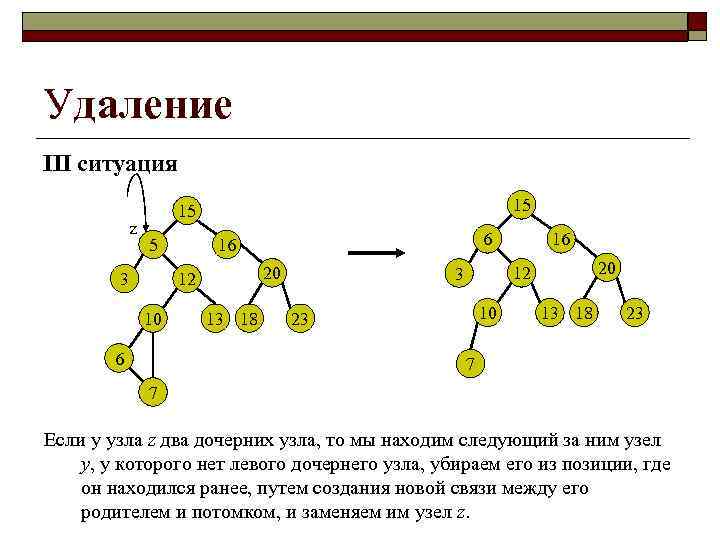
Удаление III ситуация z 15 15 5 20 12 3 10 6 6 16 13 18 16 20 12 3 10 23 13 18 23 7 7 Если у узла z два дочерних узла, то мы находим следующий за ним узел y, у которого нет левого дочернего узла, убираем его из позиции, где он находился ранее, путем создания новой связи между его родителем и потомком, и заменяем им узел z.
Псевдокод Язык С Tree_Delete(T, z) struct TNode *Tree_Delete(struct TNode *z) { struct TNode *x, *y; if (z->left == NULL || z->right == NULL) y = z; else y = Tree_Successor(z); if (y->left != NULL) x = y->left; else x = y->right; if (x != NULL) x->p = y->p; if (y->p == NULL) root = x; else if (y == y->p->left) y->p->left = x; else y->p->right = x; if (y != z) z->key = y->key; return y; } 1 if left[z] = NIL или right[z] = NIL 2 then 3 else 4 if 5 then 6 else 7 if 8 then 9 if p[y] = NIL 10 then 11 else if y = left[p[y]] 12 then 13 else 14 if 15 then 16 return y
Время работы Операции вставки и удаления в бинарном дереве поиска высоты h могут быть выполнены за время O(h).
Спасибо за внимание!
Скачать презентацию Бинарные деревья поиска Кормен Лейзерсон Ривест Штайн Алгоритмы
#12. Бинарные деревья поиска (Шеремета).ppt