БИМАТРИЧНЫЕ ИГРЫ БИМАТРИЧНАЯ ИГРА конечная бескоалиционная

БИМАТРИЧНЫЕ ИГРЫ

БИМАТРИЧНАЯ ИГРА – конечная бескоалиционная игра двух игроков, задается двумя матрицами одинакового размера , являющимися матрицами выигрышей игроков Аи. В. Стратегией игрока А является выбор строки матриц, стратегией игрока В - выбор столбца. Если игрок А выбирает , а игрок В выбирает , то они получают соответственно выигрыши и и мы можем задать игру в виде двух платёжных матриц:

Таким образом биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока А, столбец – стратегии игрока В, элементы первой матрицы выигрыши игрока А, элементы второй матрицы – выигрыши игрока В)

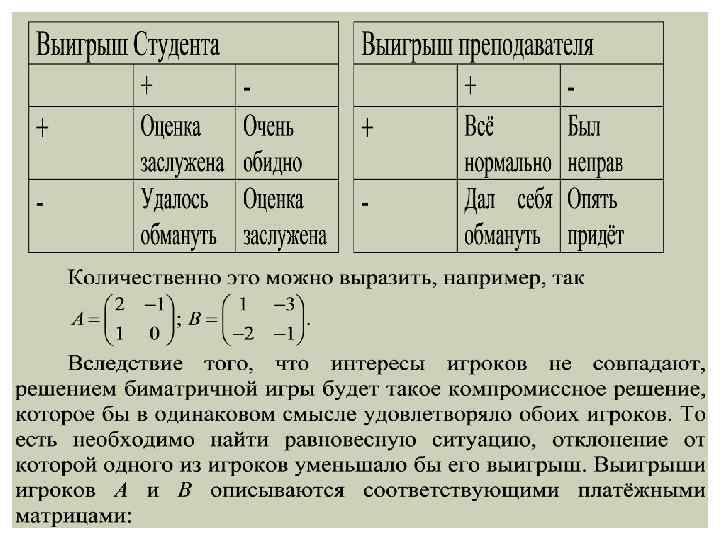
Рассмотрим следующую задачу: 1. «Дилемма узников» . Два узника находятся в предварительном заключении по подозрению в совершении преступления. Степень их осуждения определяется тем, заговорят они или будут молчать. Если оба будут молчать, то наказанием будет лишь срок предварительного заключения (потери каждого узника равны (-1)). Если оба сознаются, то получат срок, учитывающий признание как смягчающее обстоятельство (потери каждого из узников составляет (-6)). Если же заговорит только один из узников, а другой будет молчать, то заговоривший будет выпущен на свободу (его потери равны 0), а сохранивший молчание получит максимально возможное наказание (его потери будут равны (-9)).

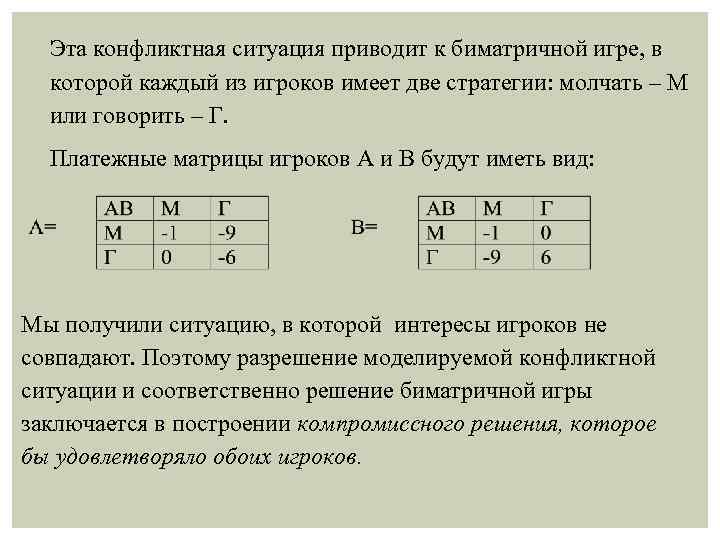
Эта конфликтная ситуация приводит к биматричной игре, в которой каждый из игроков имеет две стратегии: молчать – М или говорить – Г. Платежные матрицы игроков А и В будут иметь вид: Мы получили ситуацию, в которой интересы игроков не совпадают. Поэтому разрешение моделируемой конфликтной ситуации и соответственно решение биматричной игры заключается в построении компромиссного решения, которое бы удовлетворяло обоих игроков.

Биматричные игры 2 х2. Ситуация равновесия. Рассмотрим биматричную игру 2 х2. В этом случае платежные матрицы игроков имеют вид:

Средние выигрыши игроков А и В при использовании ими смешанных стратегий будут равны: математическое ожидание выигрыша или средний выигрыш игрока А: математическое ожидание выигрыша или средний выигрыш игрока В:

Определение 1. Будем говорить, что пара чисел: определяет равновесную ситуацию, если для любых р и q одновременно выполняются следующие неравенства:

Определение 2. Ситуация, определяемая смешанной стратегией (р*, q*), является равновесной, если отклонение от нее одного из игроков при условии, что другой сохраняет свой выбор, приводит к тому, что выигрыш отклонившегося игрока может только уменьшиться. Тем самым, получается что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку. Теорема (Дж. Нэш). Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.

Джон Нэш родился 13 июня 1928 года в Блюфилде, штат Виржиния, в строгой протестантской семье. Отец работал инженером в компании Appalachian Electric Power, мать до замужества успела 10 лет проработать школьной учительницей. В школе учился средне, а математику вообще не любил — в школе её преподавали скучно. Когда Нэшу было 14 лет, к нему в руки попала книга Эрика Т. Белла «Творцы математики» .

«Прочитав эту книгу, я сумел сам, без посторонней помощи, доказать малую теорему Ферма» — пишет Нэш в автобиографии. Так его математический гений заявил о себе. Но это было только начало. Затем последовала учёба в Политехническом институте Карнеги (ныне частный Университет Карнеги-Меллона), где Нэш пробовал изучать химию, прослушал курс международной экономики, а потом окончательно утвердился в решении заняться математикой. В 1948 году, окончив институт с двумя дипломами — бакалавра и магистра, — он поступил в Принстонский университет. Институтский преподаватель Нэша Ричард Даффин снабдил его одним из самых лаконичных рекомендательных писем. В нем была единственная строчка: «Этот человек — гений!»

В Принстоне Джон Нэш услышал о теории игр, в ту пору только представленной Джоном фон Нейманом и Оскаром Моргенштерном. Теория игр поразила его воображение, да так, что в 20 лет Джон Нэш сумел создать основы научного метода, сыгравшего огромную роль в развитии мировой экономики. В 1949 году 21 -летний учёный написал диссертацию о теории игр. Сорок пять лет спустя он получил за эту работу Нобелевскую премию по экономике. Вклад Нэша описали так: «За фундаментальный анализ равновесия в теории некооперативных игр» .

Определение 3. Ситуация в игре, приемлемая для всех игроков, называется ситуацией равновесия по Нэшу (равновесной ситуацией). Иными словами, ситуация х называется равновесной, если для любого игрока і N выполняется условие (*). В случае антагонистической игры равновесные стратегии игроков совпадают с их оптимальными стратегиями Если некоторая пара чисел (р*, q*) определяет равновесную ситуацию , то справедлива теорема:

Теорема. Выполнение неравенств равносильно выполнению неравенств

Таким образом, если пара ( р*, q*) определяет равновесную ситуацию, то неравенство: должно выполняться для двух чистых стратегий игрока A (p = 0 и р = 1) и неравенство: для двух чистых стратегий игрока В (q = 0 и q = 1). Рассмотрим разности:

Полагая: Получаем:

Пример 3. «Семейный спор» Два партнера договариваются о совместном проведении одного из двух действий, (1) и (2), каждое из которых требует их совместного участия. В случае осуществления первого из этих двух действий выигрыш первого партнера (игрок А) будет вдвое выше выигрыша второго партнера (игрок В). Если осуществляется второе из этих двух действий выигрыш игрока А будет вдвое меньше выигрыша игрока В. Если же партнеры выполнят различные действия, то выигрыш каждого из них будет равен нулю. Эта конфликтная ситуация приводит к биматричной игре, в которой каждый из игроков имеет по две стратегии. Выигрыши игроков А и В соответственно описываются следующими платёжными матрицами:

Рассмотренная биматричная игра часто рассматривается, как одновременный выбор супругами совместного развлечения: посещение оперного спектакля или хоккейного матча. При этом в посещении оперного театра жена заинтересована в большей степени, чем муж, а при посещении стадиона наблюдается обратная картина. В случае, если договориться не удаётся, день оказывается вообще испорченным.

Рассмотрим равновесную ситуацию и составим систему неравенств для этой задачи: Проанализируем систему неравенств и представим на единичном квадрате найденные ситуации

Возможны следующие случаи:

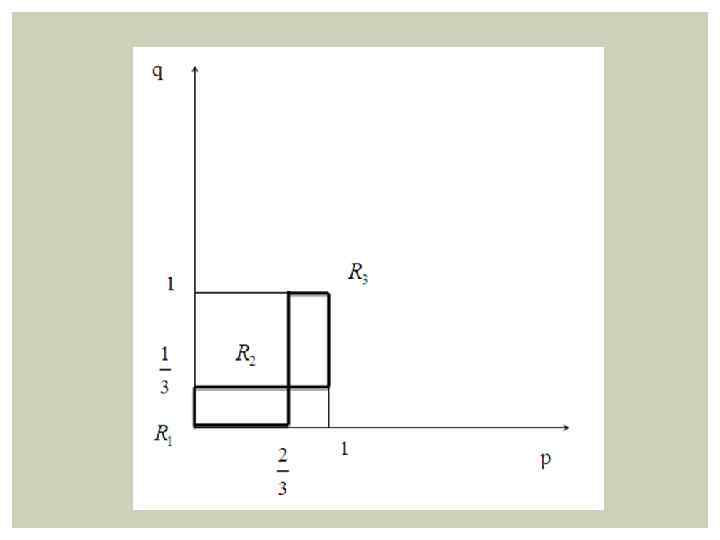
Полученные зигзаги изображены на рисунке