
БИЛЕТ № 26 Человек на качелях Студент гр. ММм-11 А. Алексенцева

Содержательная постановка 2

Концептуальная постановка Построить модель оптимального управления приседаниями с целью наискорейшей раскачки качелей (максимизации амплитуды колебаний) в рамках теории механических колебаний. При приседаниях будет происходить изменение положения центра масс человека, за счёт чего он и будет раскачиваться. Примем следующие гипотезы: 1. Человек на качелях – математический маятник с нитью переменной длины; 2. Длина нити изменяется по закону 3. Никакие случайные факторы на процесс не влияют; не учитываем температуру, влажность, атмосферное давление и т. д; 4. Влияние окружающей среды на систему сводится к воздействию силы тяжести g. 3

Концептуальная постановка Исходные данные: • рост человека ; • длина качели ; • сила тяжести Требуется найти: • оптимальную частоту приседаний 4

Математическая постановка Поведение линейной возмущающей силе системы без трения при гармонической -- угловая частота изменения нагрузки описывается уравнением движения угловая частота системы коэффициент упругости системы 5

Математическая постановка Выражение для вращательного момента Момент инерции маятника Описывается уравнением движения Ограничимся рассмотрением малых колебаний 6
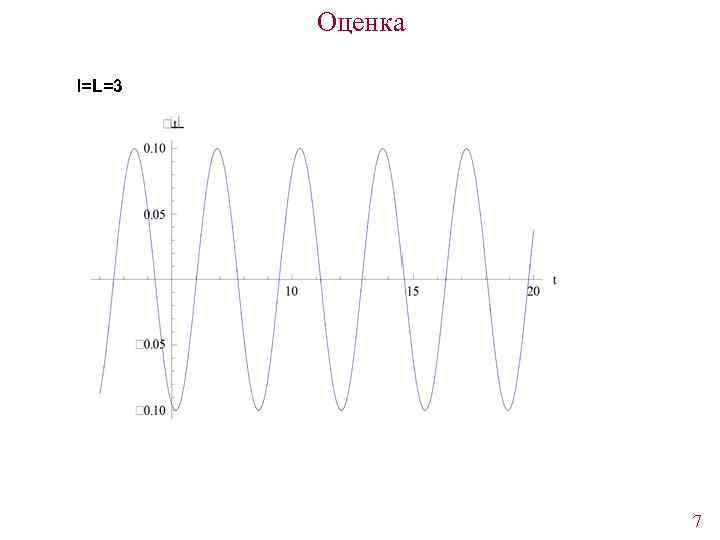
Оценка l=L=3 7
![Оценка l=3 -1. 5 Sin[0. 1 t] 8 Оценка l=3 -1. 5 Sin[0. 1 t] 8](https://present5.com/presentation/14491813_181686480/image-8.jpg)
Оценка l=3 -1. 5 Sin[0. 1 t] 8
![Оценка l=3 -1. 5 Sin[t] 9 Оценка l=3 -1. 5 Sin[t] 9](https://present5.com/presentation/14491813_181686480/image-9.jpg)
Оценка l=3 -1. 5 Sin[t] 9
![Оценка l=3 -1. 5 Sin[3 t] 10 Оценка l=3 -1. 5 Sin[3 t] 10](https://present5.com/presentation/14491813_181686480/image-10.jpg)
Оценка l=3 -1. 5 Sin[3 t] 10
![Оценка l=3 -1. 5 Sin[4 t] 11 Оценка l=3 -1. 5 Sin[4 t] 11](https://present5.com/presentation/14491813_181686480/image-11.jpg)
Оценка l=3 -1. 5 Sin[4 t] 11
![Оценка l=3 -1. 5 Sin[10 t] 12 Оценка l=3 -1. 5 Sin[10 t] 12](https://present5.com/presentation/14491813_181686480/image-12.jpg)
Оценка l=3 -1. 5 Sin[10 t] 12

Возможные пути усложнения модели 1. 2. 3. 4. 5. Учёт случайных факторов; Изменение закона для длины нити; Учёт упругости стержня качели; Учёт геометрии тела; Учёт трения…. 13

Выводы Сделаны концептуальная и математическая постановки задачи, предложены варианты усложнения модели. Численное решение ДУ – в пакете Mathematica. Известно, что для увеличения амплитуды вынужденных колебаний частота возмущающей силы должна совпасть с собственной частотой колебательной системы. Полученные результаты согласуются с этим утверждением. При амплитуда колебаний стремится к бесконечности. 14

Благодарю за внимание!