51fe800194de4bc093a84f2e9f5aba8d.ppt
- Количество слайдов: 42

Bilateral Mesh Denoising Shachar Fleishman Iddo Drori Daniel Cohen-Or Tel Aviv University

Denoising • Input (scanned) model – Additive noise + =
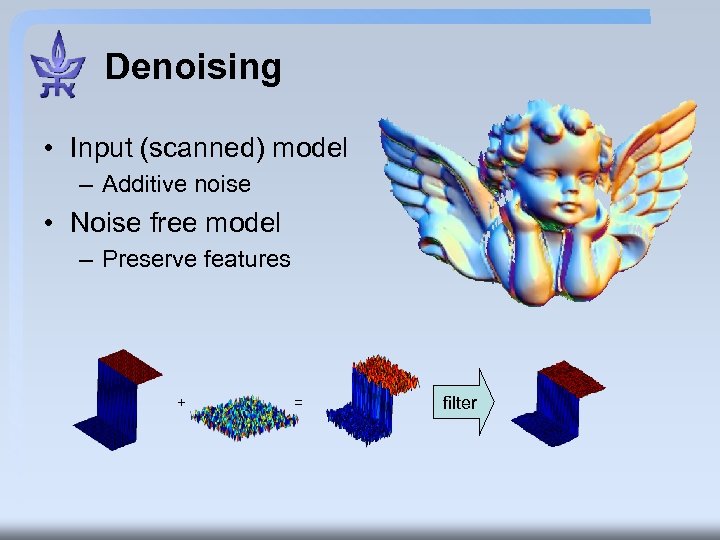
Denoising • Input (scanned) model – Additive noise • Noise free model – Preserve features + = filter
![Image denoising • Wavelet denoising [Donoho ’ 95] • Anisotropic diffusion [Perona & Malik Image denoising • Wavelet denoising [Donoho ’ 95] • Anisotropic diffusion [Perona & Malik](https://present5.com/presentation/51fe800194de4bc093a84f2e9f5aba8d/image-4.jpg)
Image denoising • Wavelet denoising [Donoho ’ 95] • Anisotropic diffusion [Perona & Malik ’ 90] • Bilateral filter [Smith & Brady ’ 97], [Tomasi & Manduchi ’ 98] • [Black et al. ’ 98] – Anisotropic diffusion – Robust statistics • [Elad ’ 01], [Durand & Dorsey ’ 02] relate – Anisotropic diffusion – Robust statistics – Bilateral filter

Original and noisy ( 2=900) images Images courtesy of Michael Elad

TV filtering: 50 iterations 10 iterations (MSE=146. 3339) (MSE=131. 5013) Images courtesy of Michael Elad

Wavelet Denoising (soft) Using DB 5 Using DB 3 (MSE=144. 7436) (MSE=150. 7006) Images courtesy of Michael Elad

Filtering via the Bilateral 2 iterations with 11 11 Sub-gradient based 5 5 (MSE=89. 2516) (MSE=93. 4024) Images courtesy of Michael Elad

Mesh denoising, smoothing and fairing • Adapt image denoising algorithms to meshes – Wiener filter [Peng et al. ’ 01] – Isotropic diffusion [Desbrun et al. ’ 99] – Anisotropic diffusion of height fields [Desbrun et al. ’ 00] – Anisotropic diffusion on meshes [Clarenz et al. ’ 00, Xu & Bajaj ’ 03] – Bilateral filter [Choudhury & Tumblin ’ 03] [Jones et al. ’ 03]

Bilateral mesh denoising • Fast • Simple • Intuitive parameter selection

Bilateral filtering • Gaussian filter * =
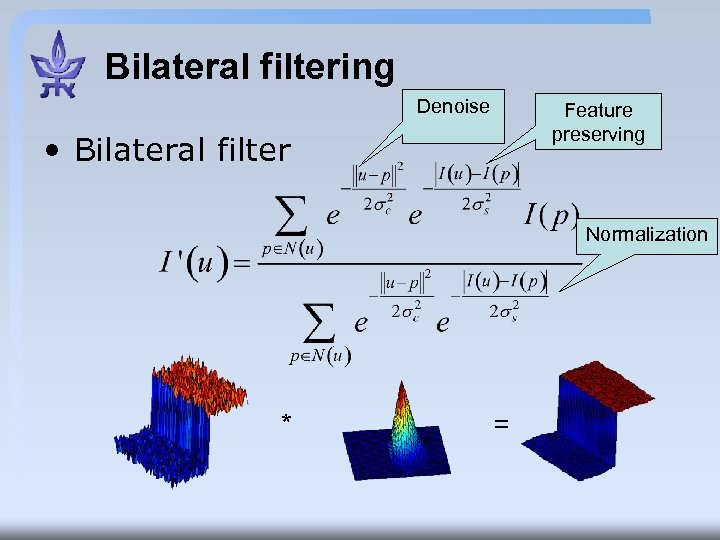
Bilateral filtering Denoise Feature preserving • Bilateral filter Normalization * =

Bilateral filtering of meshes
Bilateral filtering of meshes

Bilateral filtering of meshes • Height above surface is equivalent to the gray level values in images

Bilateral filtering of meshes • Height above surface is equivalent to the gray level values in images • Apply the bilateral filter to heights

Bilateral filtering of meshes • Height above surface is equivalent to the gray level values in images • Apply the bilateral filter to heights • Move the vertex to its new height

Bilateral filtering of meshes • Height above surface is equivalent to the gray level values in images • Apply the bilateral filter to heights • Move the vertex to its new height • In practice: – Sharp features
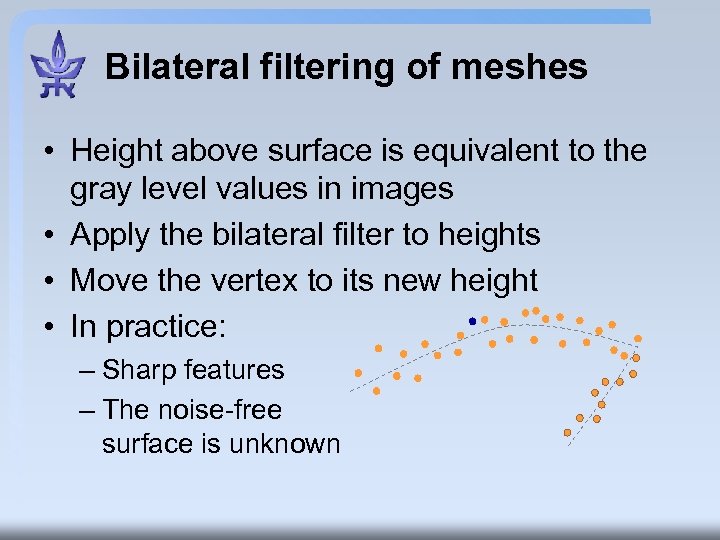
Bilateral filtering of meshes • Height above surface is equivalent to the gray level values in images • Apply the bilateral filter to heights • Move the vertex to its new height • In practice: – Sharp features – The noise-free surface is unknown

Solution • A plane that passes through the point is the estimator to the smooth surface • Plane L=(p, n) n P L
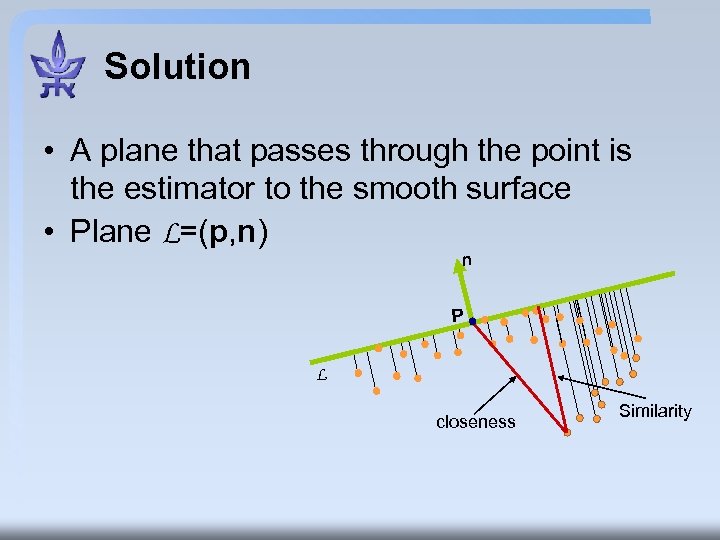
Solution • A plane that passes through the point is the estimator to the smooth surface • Plane L=(p, n) n P L closeness Similarity
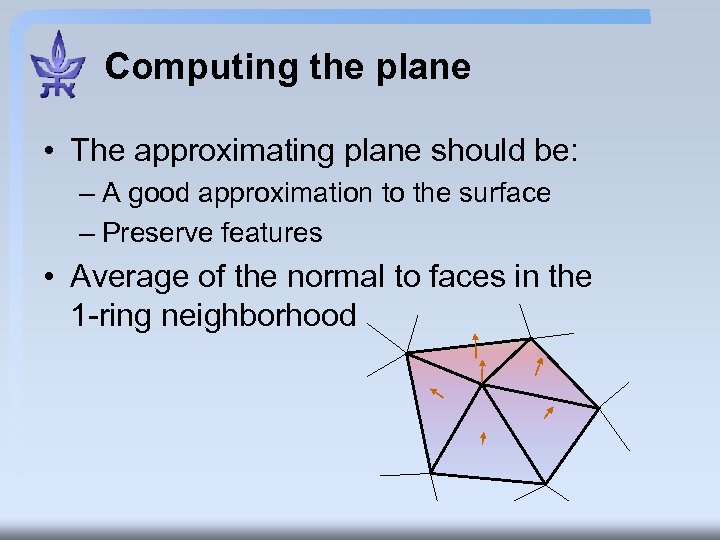
Computing the plane • The approximating plane should be: – A good approximation to the surface – Preserve features • Average of the normal to faces in the 1 -ring neighborhood
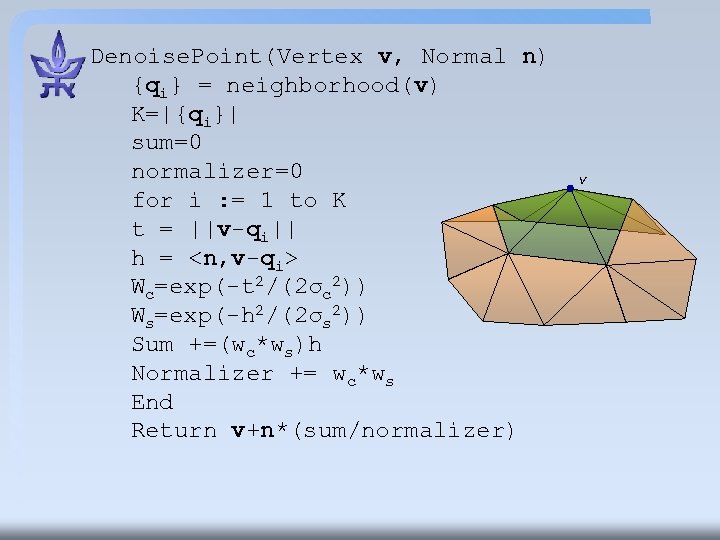
Denoise. Point(Vertex v, Normal n) {qi} = neighborhood(v) K=|{qi}| sum=0 normalizer=0 for i : = 1 to K t = ||v-qi|| h = <n, v-qi> Wc=exp(-t 2/(2σc 2)) Ws=exp(-h 2/(2σs 2)) Sum +=(wc*ws)h Normalizer += wc*ws End Return v+n*(sum/normalizer) v
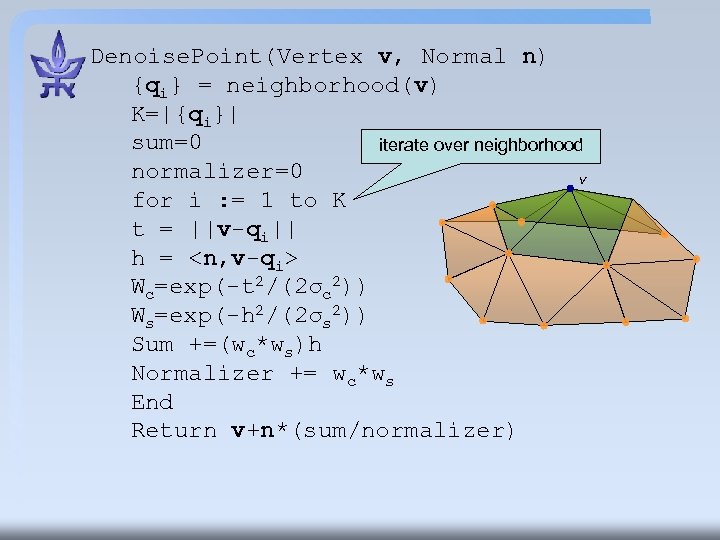
Denoise. Point(Vertex v, Normal n) {qi} = neighborhood(v) K=|{qi}| sum=0 iterate over neighborhood normalizer=0 v for i : = 1 to K t = ||v-qi|| h = <n, v-qi> Wc=exp(-t 2/(2σc 2)) Ws=exp(-h 2/(2σs 2)) Sum +=(wc*ws)h Normalizer += wc*ws End Return v+n*(sum/normalizer)
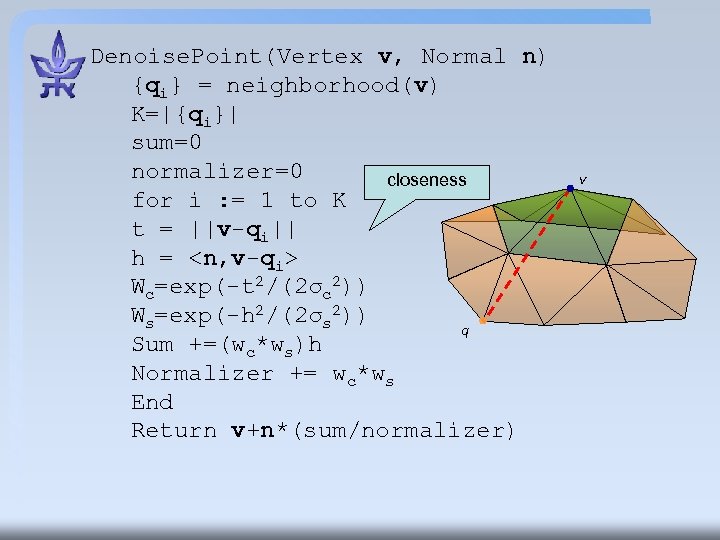
Denoise. Point(Vertex v, Normal n) {qi} = neighborhood(v) K=|{qi}| sum=0 normalizer=0 closeness for i : = 1 to K t = ||v-qi|| h = <n, v-qi> Wc=exp(-t 2/(2σc 2)) Ws=exp(-h 2/(2σs 2)) q Sum +=(wc*ws)h Normalizer += wc*ws End Return v+n*(sum/normalizer) v
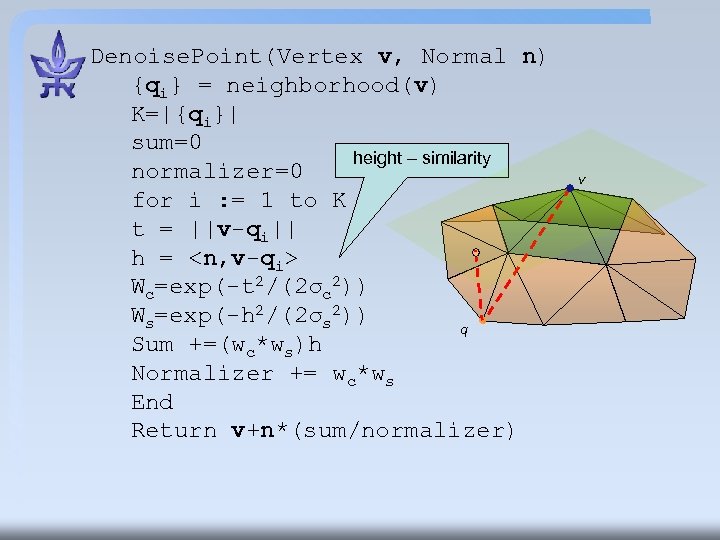
Denoise. Point(Vertex v, Normal n) {qi} = neighborhood(v) K=|{qi}| sum=0 height – similarity normalizer=0 for i : = 1 to K t = ||v-qi|| h = <n, v-qi> Wc=exp(-t 2/(2σc 2)) Ws=exp(-h 2/(2σs 2)) q Sum +=(wc*ws)h Normalizer += wc*ws End Return v+n*(sum/normalizer) v
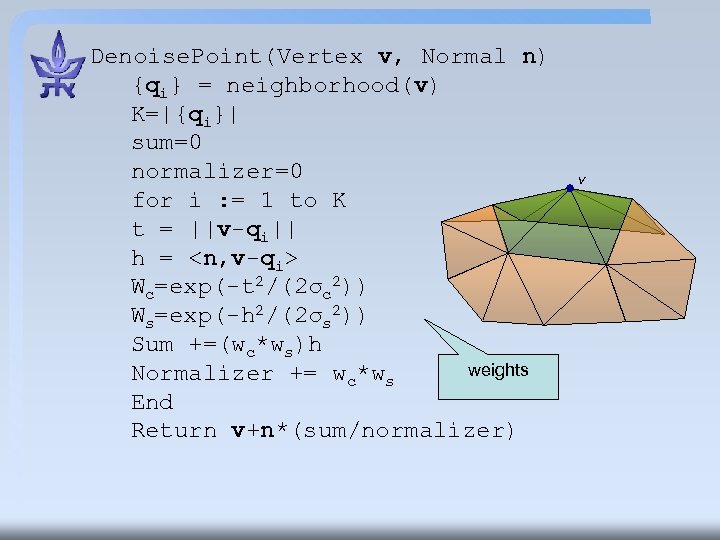
Denoise. Point(Vertex v, Normal n) {qi} = neighborhood(v) K=|{qi}| sum=0 normalizer=0 for i : = 1 to K t = ||v-qi|| h = <n, v-qi> Wc=exp(-t 2/(2σc 2)) Ws=exp(-h 2/(2σs 2)) Sum +=(wc*ws)h weights Normalizer += wc*ws End Return v+n*(sum/normalizer) v
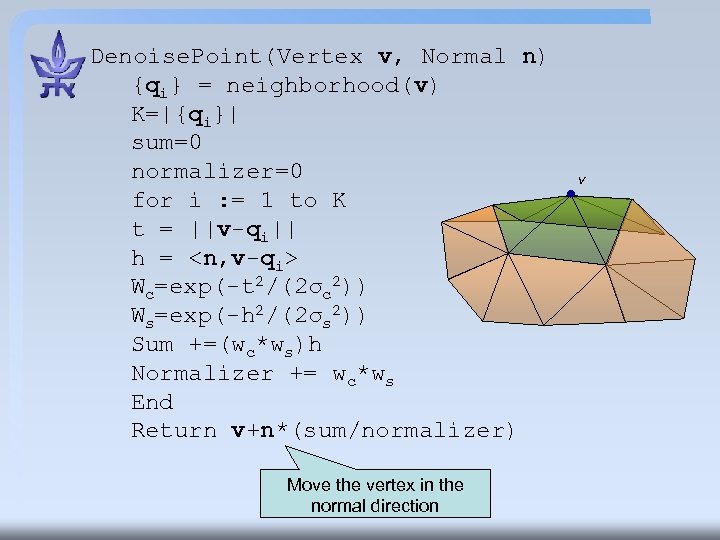
Denoise. Point(Vertex v, Normal n) {qi} = neighborhood(v) K=|{qi}| sum=0 normalizer=0 for i : = 1 to K t = ||v-qi|| h = <n, v-qi> Wc=exp(-t 2/(2σc 2)) Ws=exp(-h 2/(2σs 2)) Sum +=(wc*ws)h Normalizer += wc*ws End Return v+n*(sum/normalizer) Move the vertex in the normal direction v
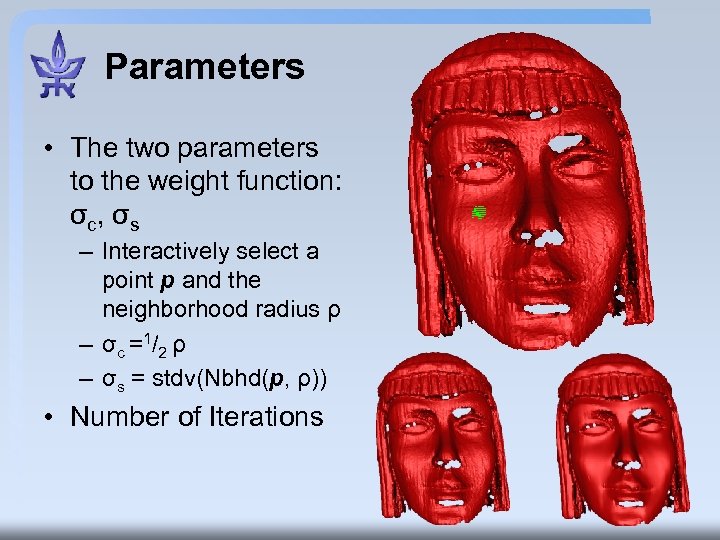
Parameters • The two parameters to the weight function: σc, σs – Interactively select a point p and the neighborhood radius ρ – σ c = 1/ 2 ρ – σs = stdv(Nbhd(p, ρ)) • Number of Iterations
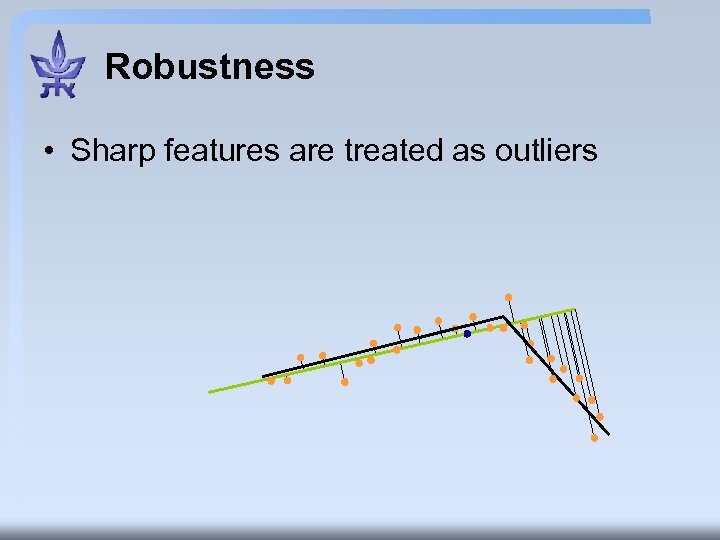
Robustness • Sharp features are treated as outliers

Robustness • Sharp features are treated as outliers • The bilateral filter does not recover smoothed signal
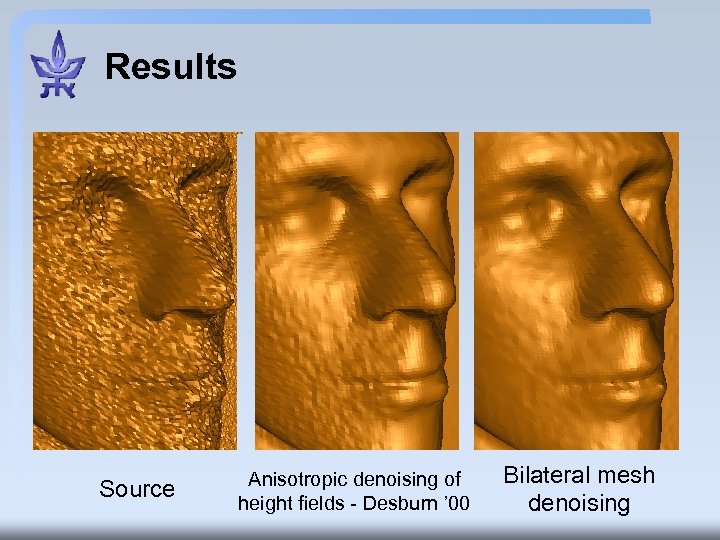
Results Source Anisotropic denoising of height fields - Desburn ’ 00 Bilateral mesh denoising
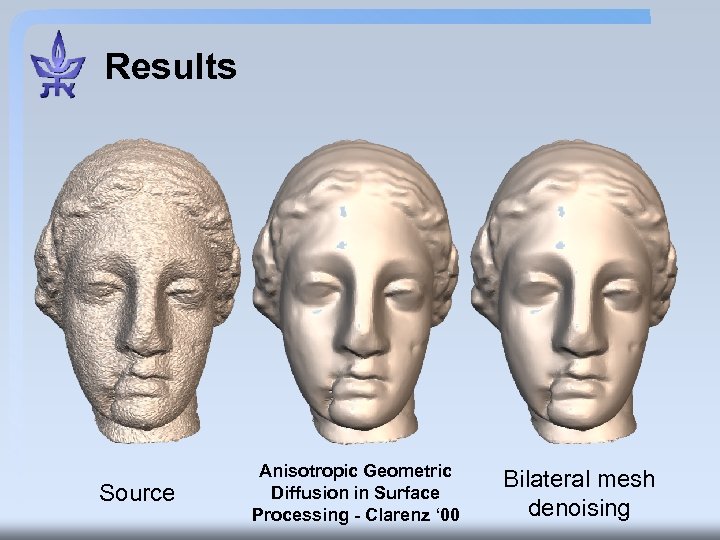
Results Source Anisotropic Geometric Diffusion in Surface Processing - Clarenz ‘ 00 Bilateral mesh denoising
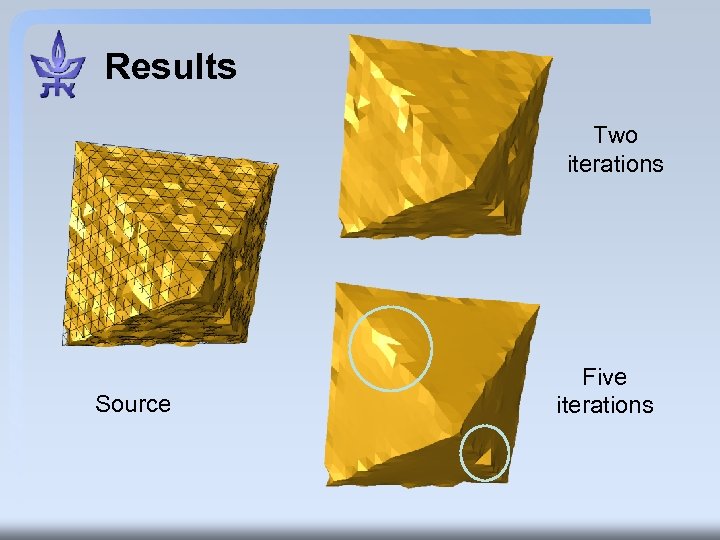
Results Two iterations Source Five iterations


Future Work • Adapt the algorithm to point sets • Robust estimator of normals

Acknowledgements • Models and images courtesy of Jean-Yves Bouguet, Mathieu Desbrun, Alexander Belyaev, Christian Rossl from Max Planck Insitut fur Informatik, Udo Diewald and Michael Elad • Israel Science Foundation funded by the Israel Academy of Sciences and Humanities • Israeli Ministry of Science • A grant from the German Israel Foundation (GIF).
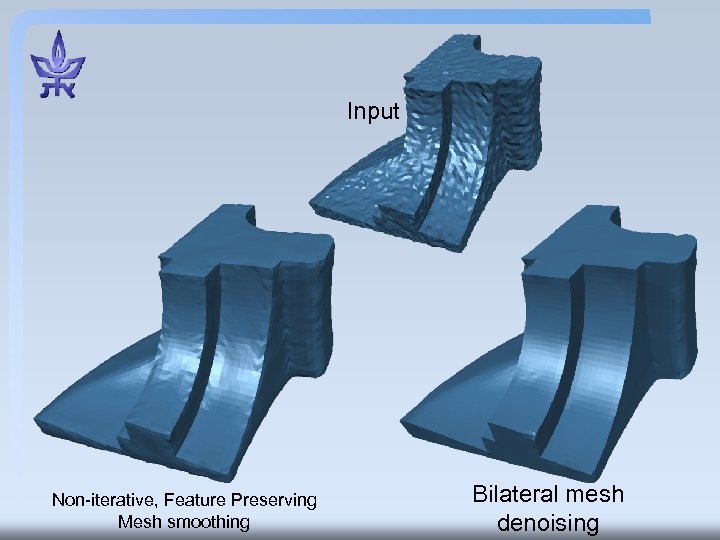
Input Non-iterative, Feature Preserving Mesh smoothing Bilateral mesh denoising
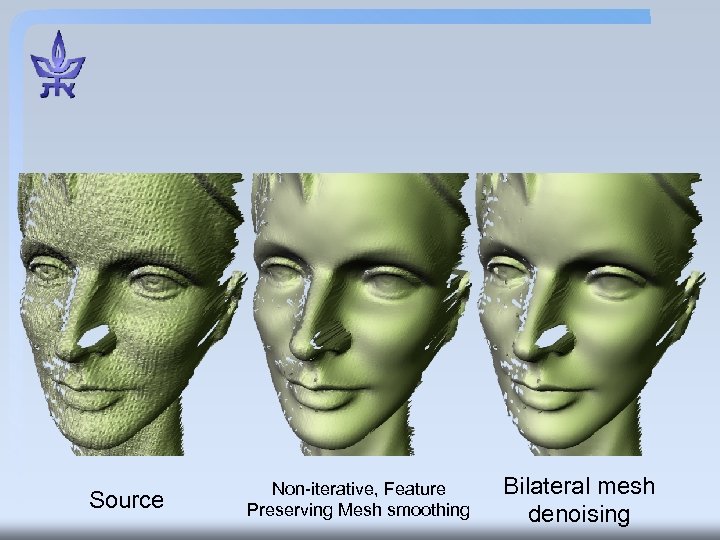
Source Non-iterative, Feature Preserving Mesh smoothing Bilateral mesh denoising
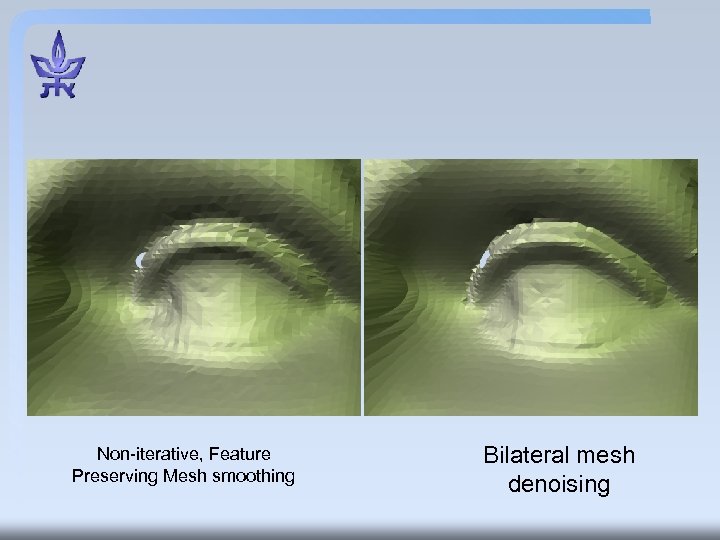
Non-iterative, Feature Preserving Mesh smoothing Bilateral mesh denoising
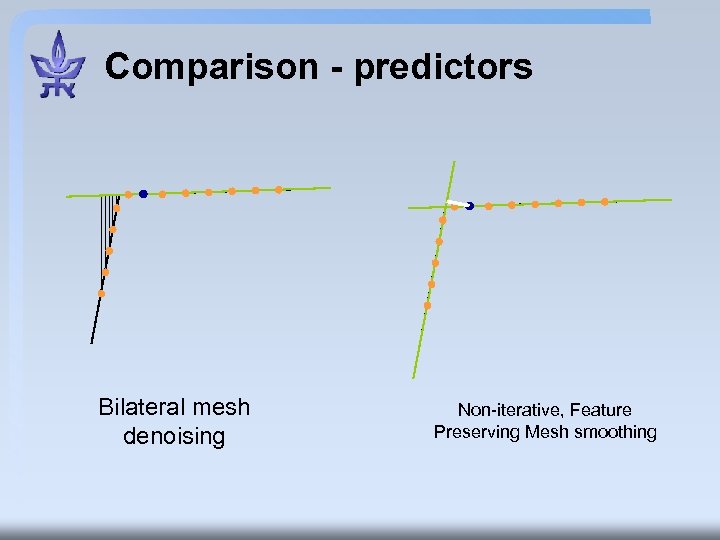
Comparison - predictors Bilateral mesh denoising Non-iterative, Feature Preserving Mesh smoothing

New results Bilateral mesh denoising Extended Bilateral mesh denoising
51fe800194de4bc093a84f2e9f5aba8d.ppt