2b5d3858ba787c2ae154b2376134aef6.ppt
- Количество слайдов: 47

BIBLIOGRAFIA • Bernard J. Hamrock, Elementos de máquinas. Ed. Mc Graw Hill. • Robert L. Norton, Diseño de máquinas. Ed. Prentice Hall. • Shigley, Diseño en Ingeniería Mecánica, Ed. Mc Graw-Hill

Load, Stress and Strain When I am working on a problem, I never think about beauty. I only think of how to solve the problem. But when I have finished, if the solution is not beautiful, I know it is wrong. Richard Buckminster Fuller Image: A dragline lifts a large load in a mining operation.
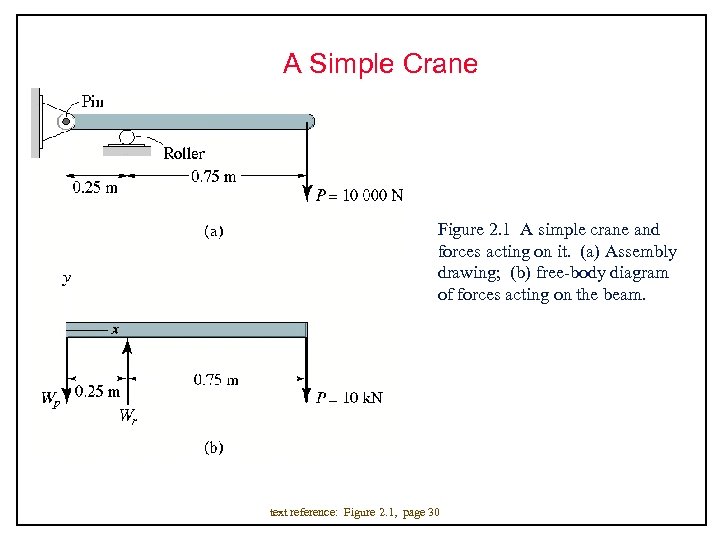
A Simple Crane Figure 2. 1 A simple crane and forces acting on it. (a) Assembly drawing; (b) free-body diagram of forces acting on the beam. text reference: Figure 2. 1, page 30
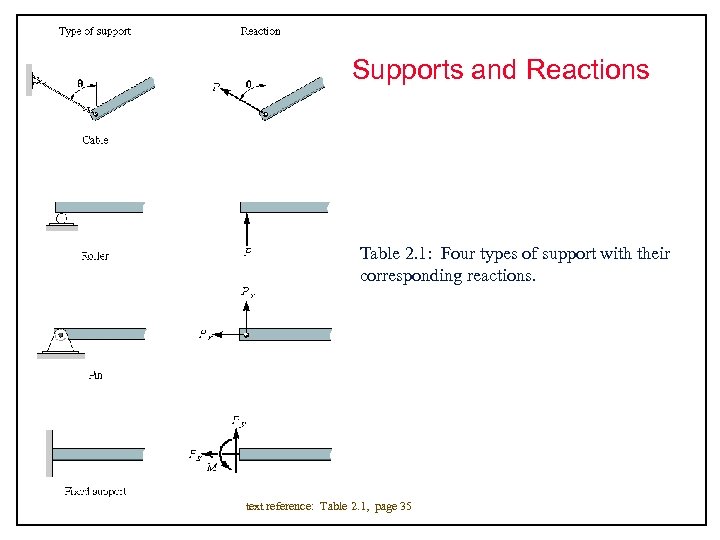
Supports and Reactions Table 2. 1: Four types of support with their corresponding reactions. text reference: Table 2. 1, page 35
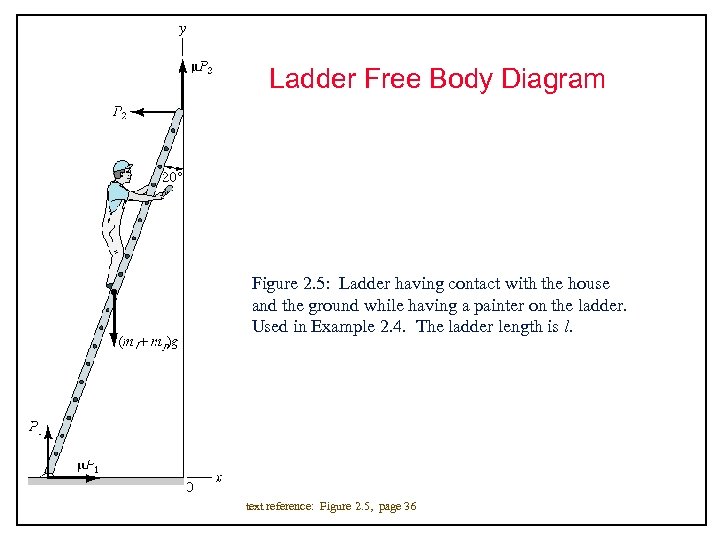
Ladder Free Body Diagram Figure 2. 5: Ladder having contact with the house and the ground while having a painter on the ladder. Used in Example 2. 4. The ladder length is l. text reference: Figure 2. 5, page 36
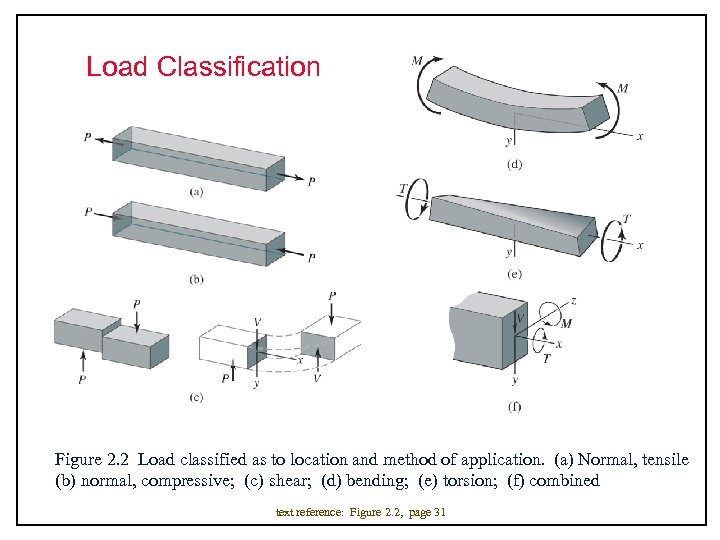
Load Classification Figure 2. 2 Load classified as to location and method of application. (a) Normal, tensile (b) normal, compressive; (c) shear; (d) bending; (e) torsion; (f) combined text reference: Figure 2. 2, page 31
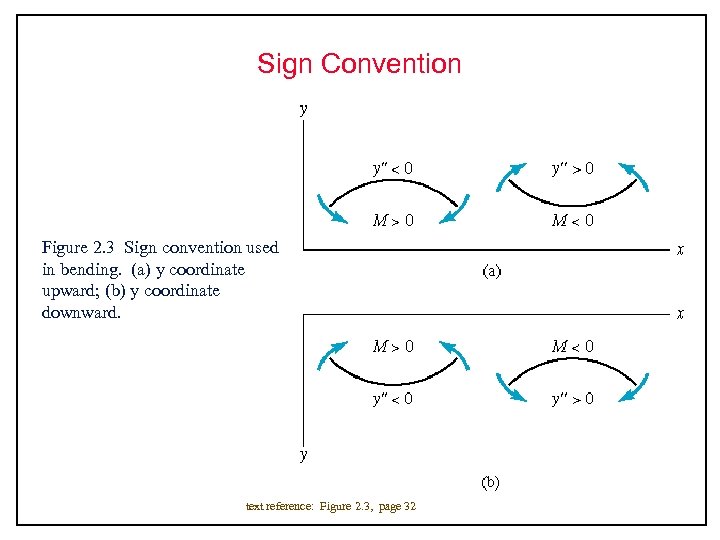
Sign Convention Figure 2. 3 Sign convention used in bending. (a) y coordinate upward; (b) y coordinate downward. text reference: Figure 2. 3, page 32
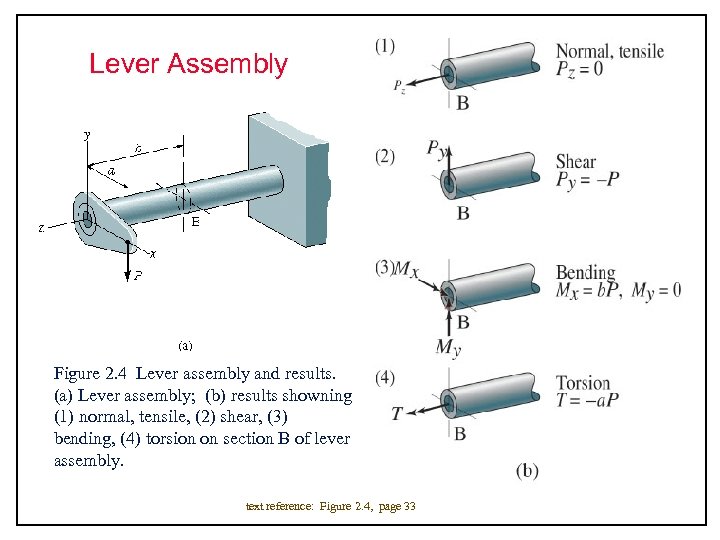
Lever Assembly Figure 2. 4 Lever assembly and results. (a) Lever assembly; (b) results showning (1) normal, tensile, (2) shear, (3) bending, (4) torsion on section B of lever assembly. text reference: Figure 2. 4, page 33
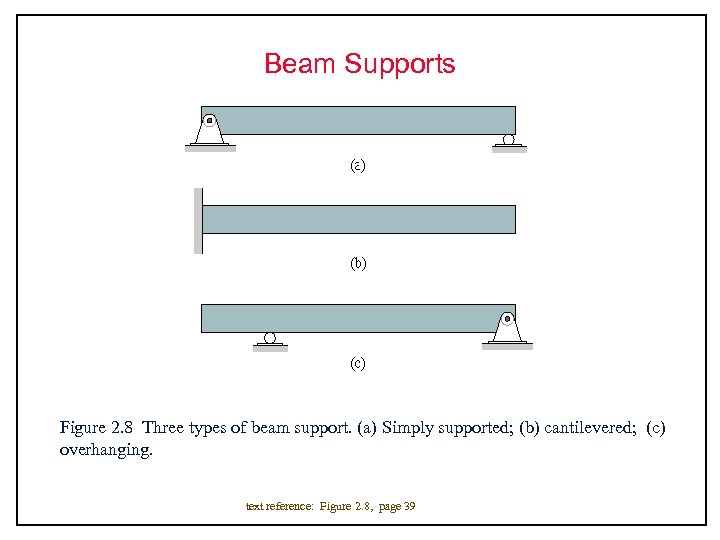
Beam Supports Figure 2. 8 Three types of beam support. (a) Simply supported; (b) cantilevered; (c) overhanging. text reference: Figure 2. 8, page 39
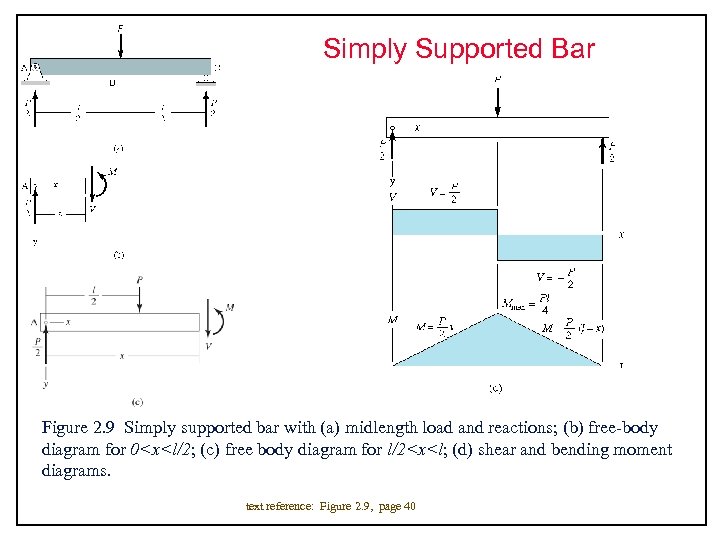
Simply Supported Bar Figure 2. 9 Simply supported bar with (a) midlength load and reactions; (b) free-body diagram for 0<x<l/2; (c) free body diagram for l/2<x<l; (d) shear and bending moment diagrams. text reference: Figure 2. 9, page 40

Singularity Functions (Part 1) Table 2. 2 Six singularity and load intensity functions with corresponding graphs and expressions. text reference: Table 2. 2, page 43
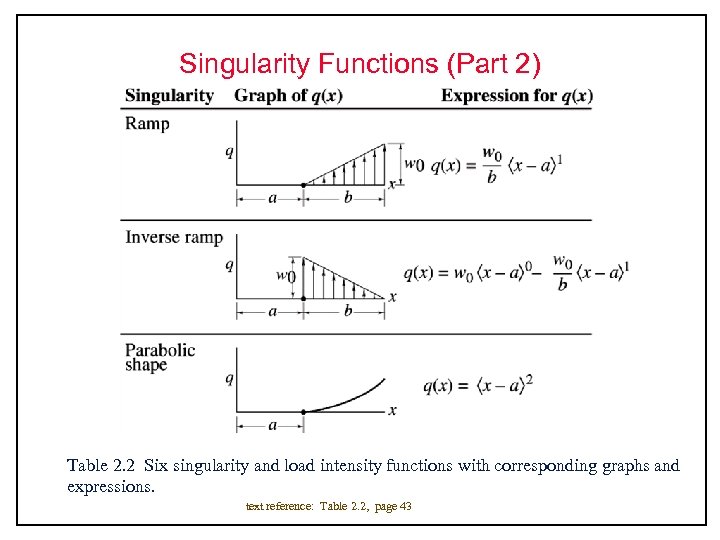
Singularity Functions (Part 2) Table 2. 2 Six singularity and load intensity functions with corresponding graphs and expressions. text reference: Table 2. 2, page 43
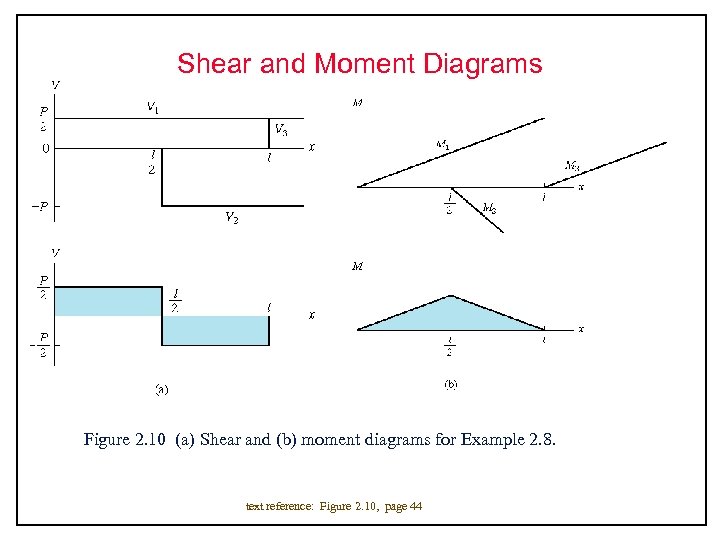
Shear and Moment Diagrams Figure 2. 10 (a) Shear and (b) moment diagrams for Example 2. 8. text reference: Figure 2. 10, page 44
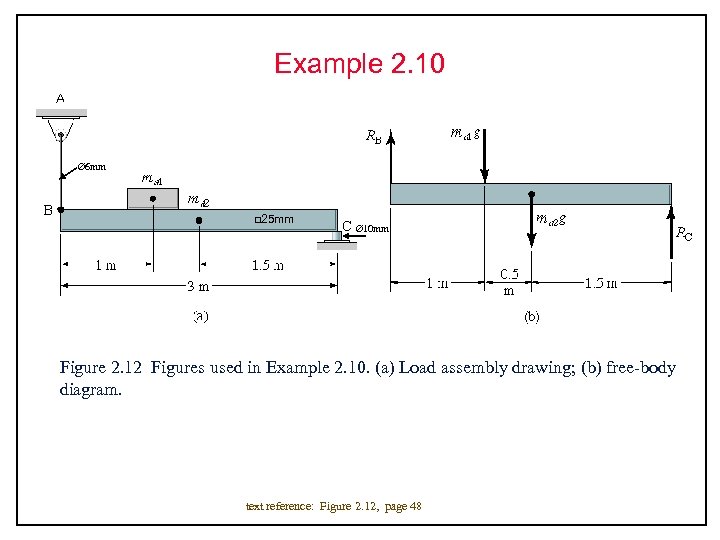
Example 2. 10 Ø 6 mm □ 25 mm Ø 10 mm Figure 2. 12 Figures used in Example 2. 10. (a) Load assembly drawing; (b) free-body diagram. text reference: Figure 2. 12, page 48
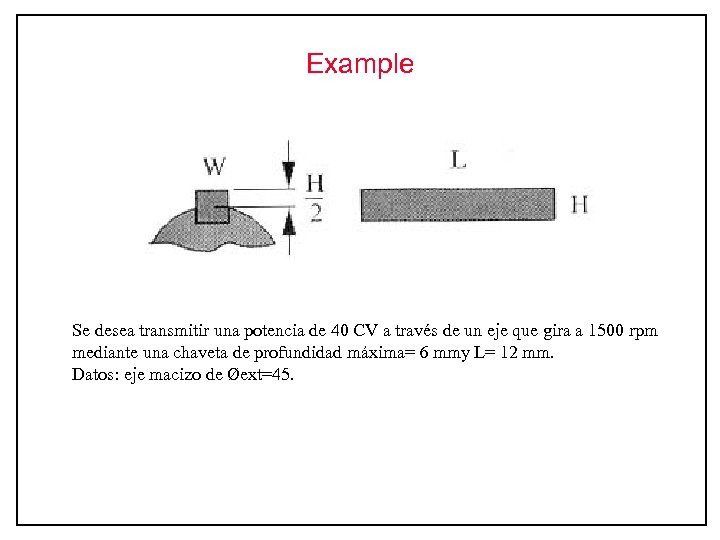
Example Se desea transmitir una potencia de 40 CV a través de un eje que gira a 1500 rpm mediante una chaveta de profundidad máxima= 6 mmy L= 12 mm. Datos: eje macizo de Øext=45.
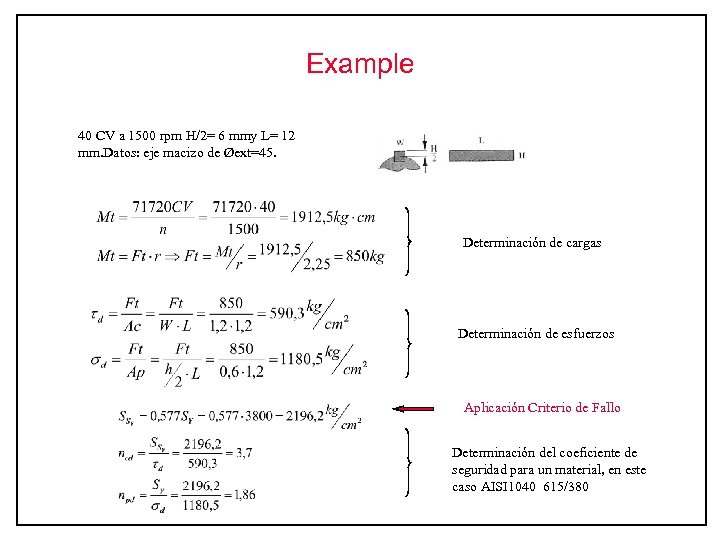
Example 40 CV a 1500 rpm H/2= 6 mmy L= 12 mm. Datos: eje macizo de Øext=45. Determinación de cargas Determinación de esfuerzos Aplicación Criterio de Fallo Determinación del coeficiente de seguridad para un material, en este caso AISI 1040 615/380
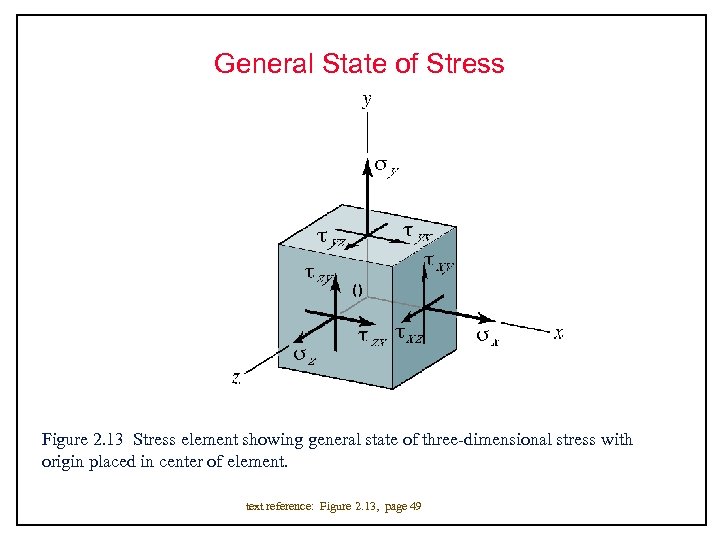
General State of Stress Figure 2. 13 Stress element showing general state of three-dimensional stress with origin placed in center of element. text reference: Figure 2. 13, page 49
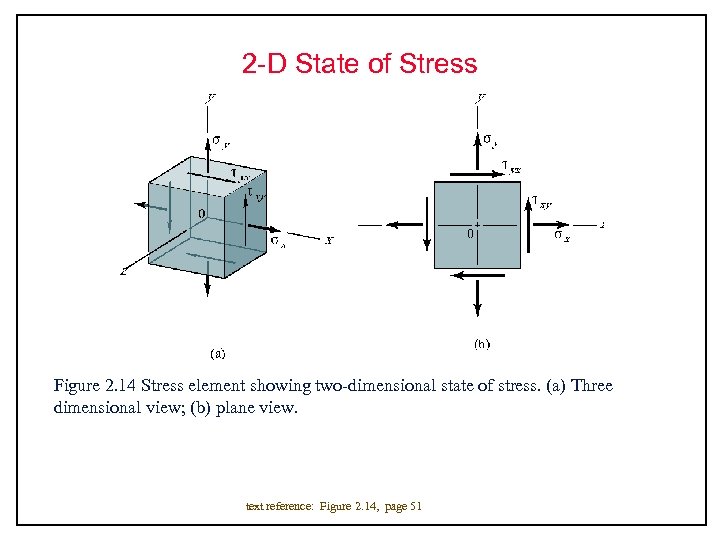
2 -D State of Stress Figure 2. 14 Stress element showing two-dimensional state of stress. (a) Three dimensional view; (b) plane view. text reference: Figure 2. 14, page 51
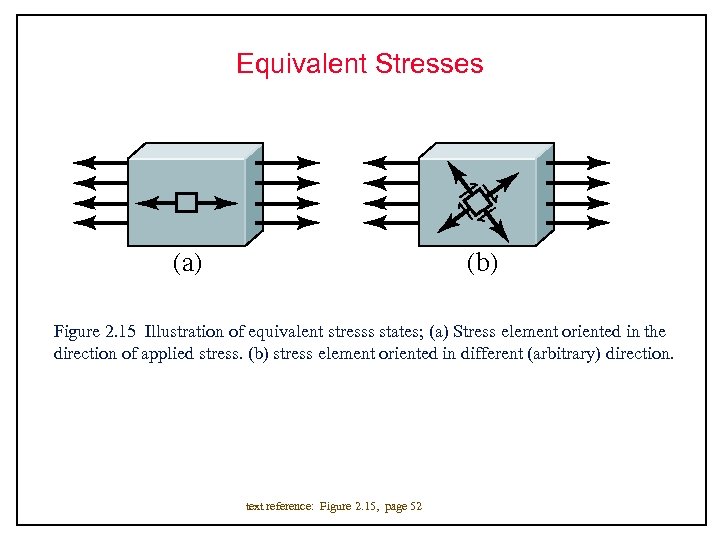
Equivalent Stresses Figure 2. 15 Illustration of equivalent stresss states; (a) Stress element oriented in the direction of applied stress. (b) stress element oriented in different (arbitrary) direction. text reference: Figure 2. 15, page 52
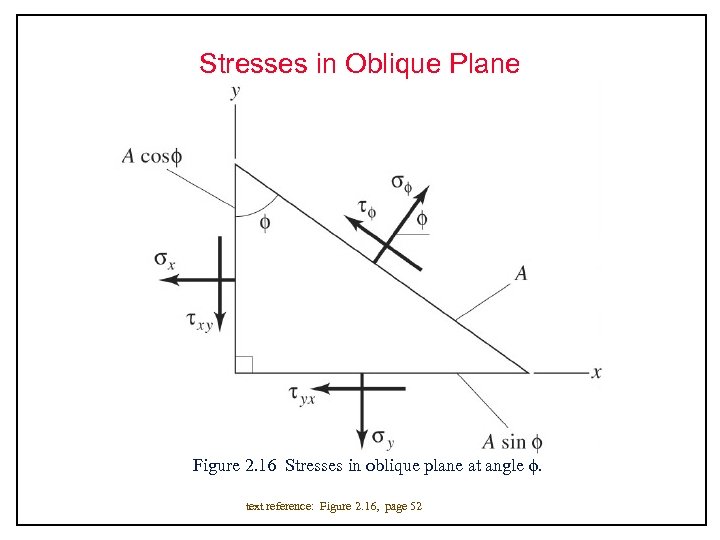
Stresses in Oblique Plane Figure 2. 16 Stresses in oblique plane at angle . text reference: Figure 2. 16, page 52

Stresses in Oblique Plane text reference: Shigley pag 28, 29
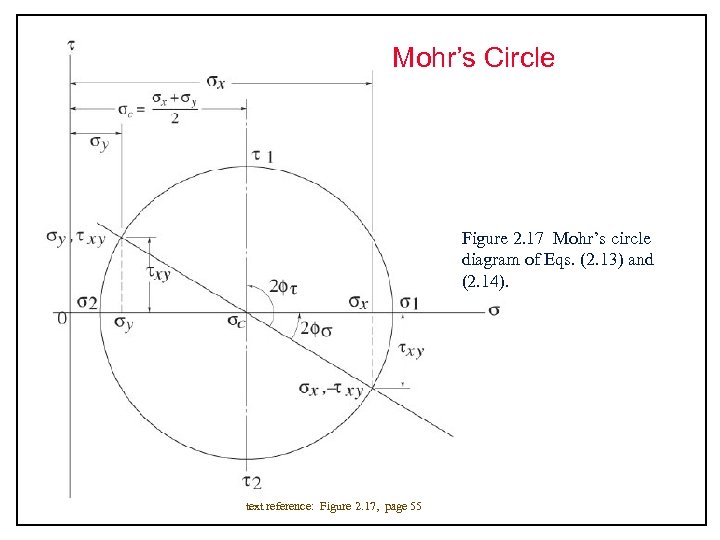
Mohr’s Circle Figure 2. 17 Mohr’s circle diagram of Eqs. (2. 13) and (2. 14). text reference: Figure 2. 17, page 55

Mohr’s Circle Example Un elemento con el siguiente estado tensional. Se desea: a) hallar los esfuerzos y las direcciones principales e indicar en el elemento su orientación correcta, con respecto al sistema xy. Se trazará otro elemento en que se muestren T 1 y T 2, determinando los esfuerzos normales correspondientes y marcando los signos letras. text reference: Shigley, page 31 -32
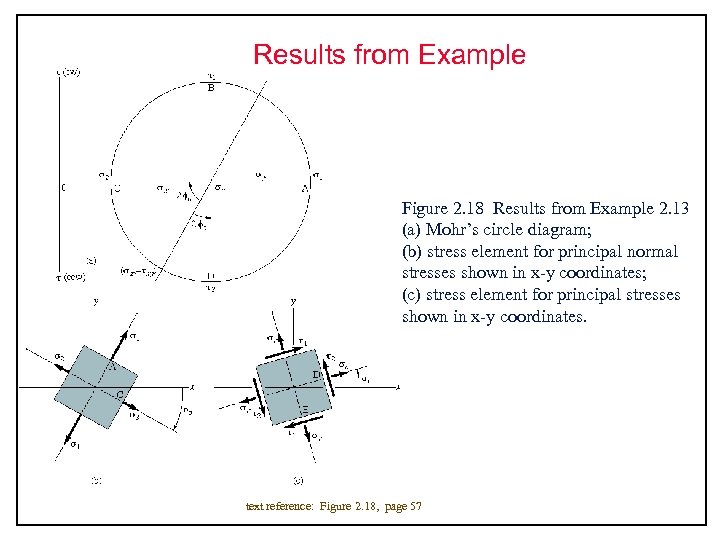
Results from Example Figure 2. 18 Results from Example 2. 13 (a) Mohr’s circle diagram; (b) stress element for principal normal stresses shown in x-y coordinates; (c) stress element for principal stresses shown in x-y coordinates. text reference: Figure 2. 18, page 57
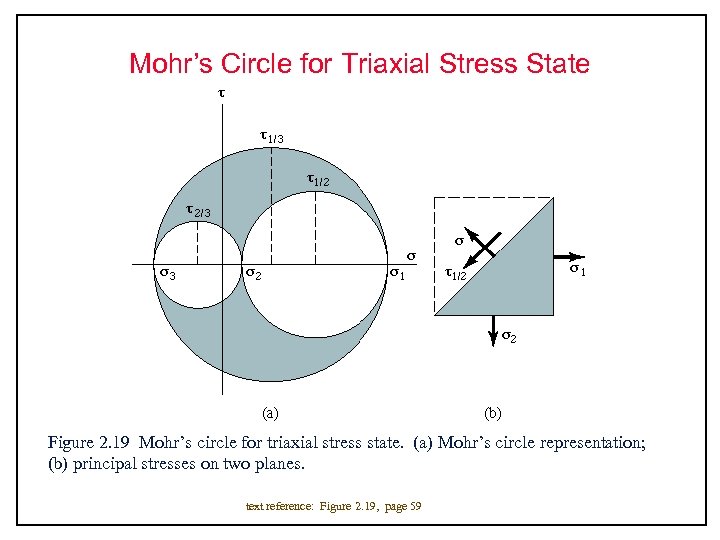
Mohr’s Circle for Triaxial Stress State Figure 2. 19 Mohr’s circle for triaxial stress state. (a) Mohr’s circle representation; (b) principal stresses on two planes. text reference: Figure 2. 19, page 59
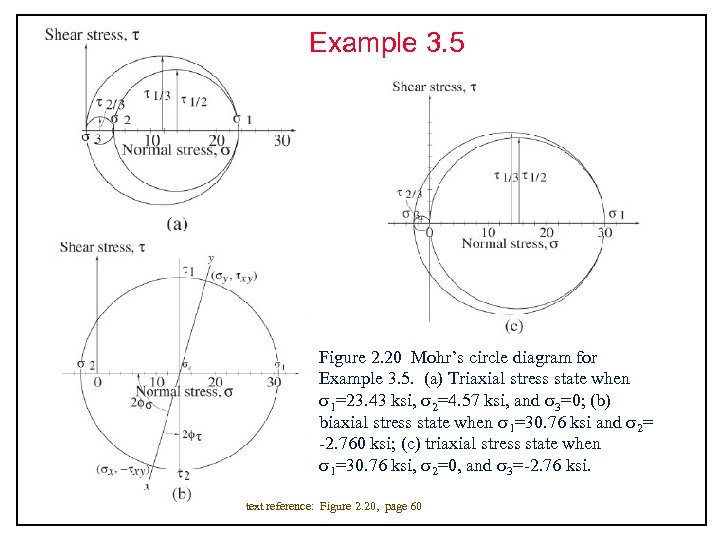
Example 3. 5 Figure 2. 20 Mohr’s circle diagram for Example 3. 5. (a) Triaxial stress state when 1=23. 43 ksi, 2=4. 57 ksi, and 3=0; (b) biaxial stress state when 1=30. 76 ksi and 2= -2. 760 ksi; (c) triaxial stress state when 1=30. 76 ksi, 2=0, and 3=-2. 76 ksi. text reference: Figure 2. 20, page 60
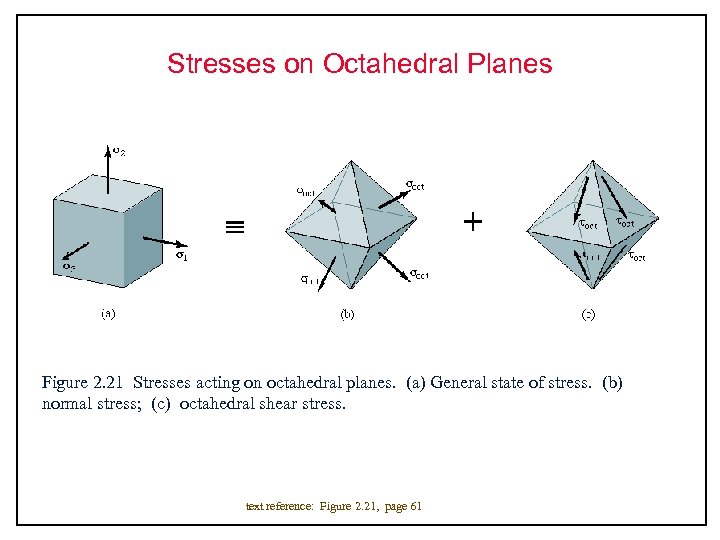
Stresses on Octahedral Planes Figure 2. 21 Stresses acting on octahedral planes. (a) General state of stress. (b) normal stress; (c) octahedral shear stress. text reference: Figure 2. 21, page 61
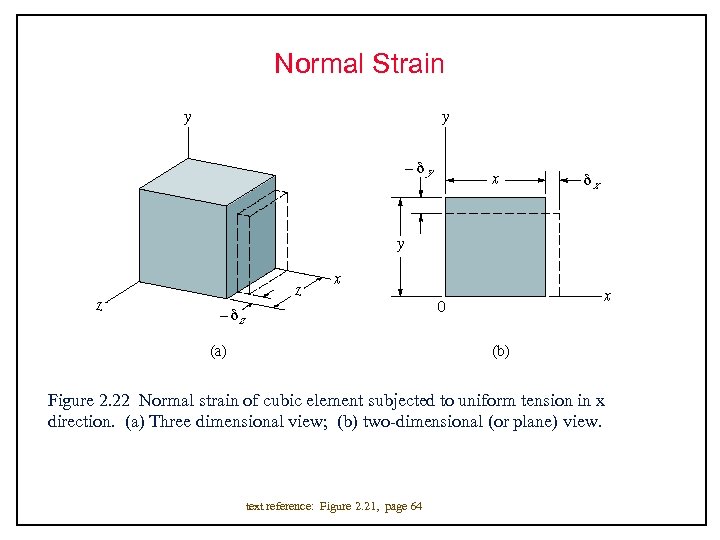
Normal Strain Figure 2. 22 Normal strain of cubic element subjected to uniform tension in x direction. (a) Three dimensional view; (b) two-dimensional (or plane) view. text reference: Figure 2. 21, page 64
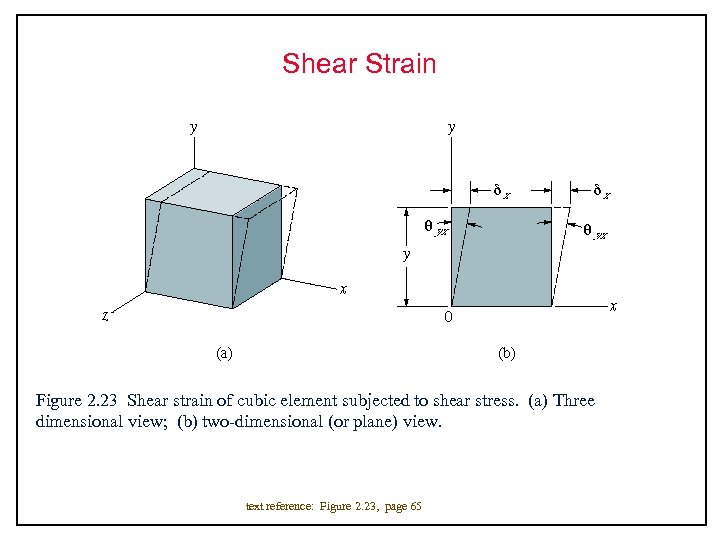
Shear Strain Figure 2. 23 Shear strain of cubic element subjected to shear stress. (a) Three dimensional view; (b) two-dimensional (or plane) view. text reference: Figure 2. 23, page 65
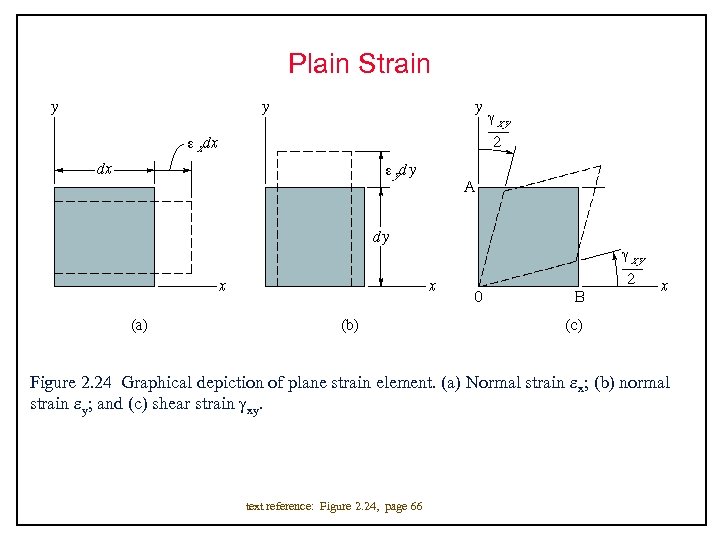
Plain Strain Figure 2. 24 Graphical depiction of plane strain element. (a) Normal strain x; (b) normal strain y; and (c) shear strain xy. text reference: Figure 2. 24, page 66
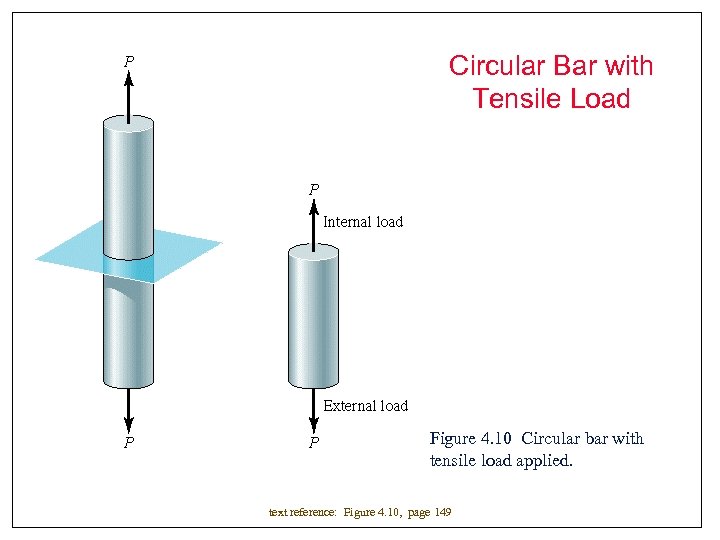
Circular Bar with Tensile Load Figure 4. 10 Circular bar with tensile load applied. text reference: Figure 4. 10, page 149

Example text reference: Figure 2. 12, page 48
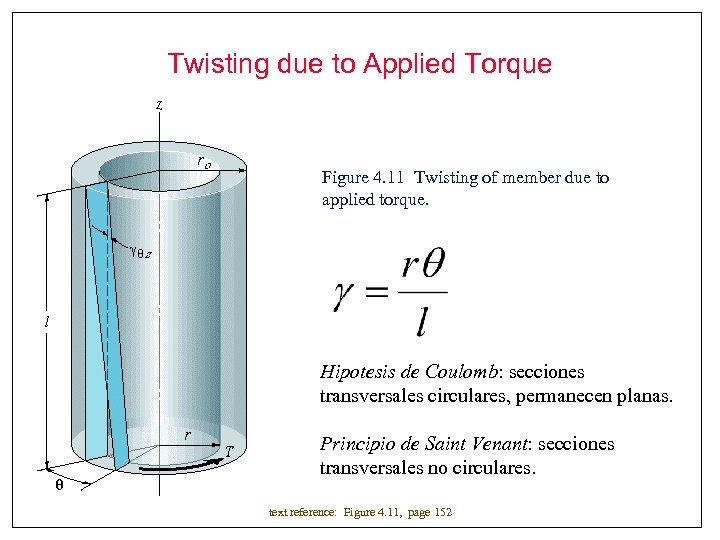
Twisting due to Applied Torque Figure 4. 11 Twisting of member due to applied torque. Hipotesis de Coulomb: secciones transversales circulares, permanecen planas. Principio de Saint Venant: secciones transversales no circulares. text reference: Figure 4. 11, page 152
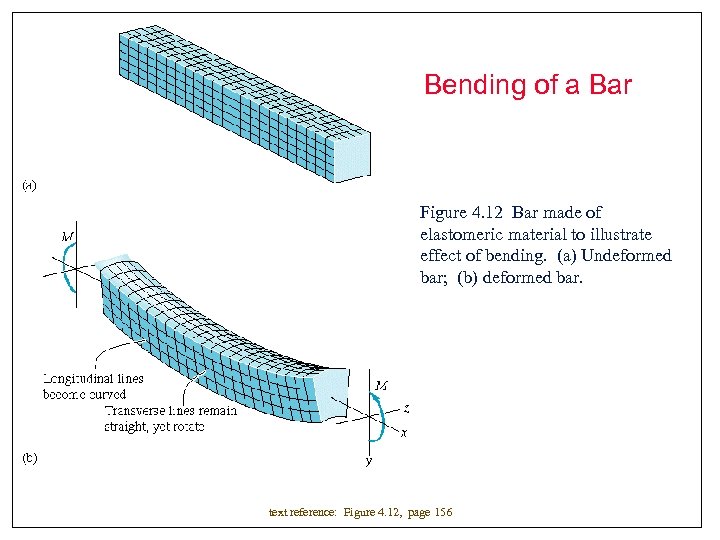
Bending of a Bar Figure 4. 12 Bar made of elastomeric material to illustrate effect of bending. (a) Undeformed bar; (b) deformed bar. text reference: Figure 4. 12, page 156
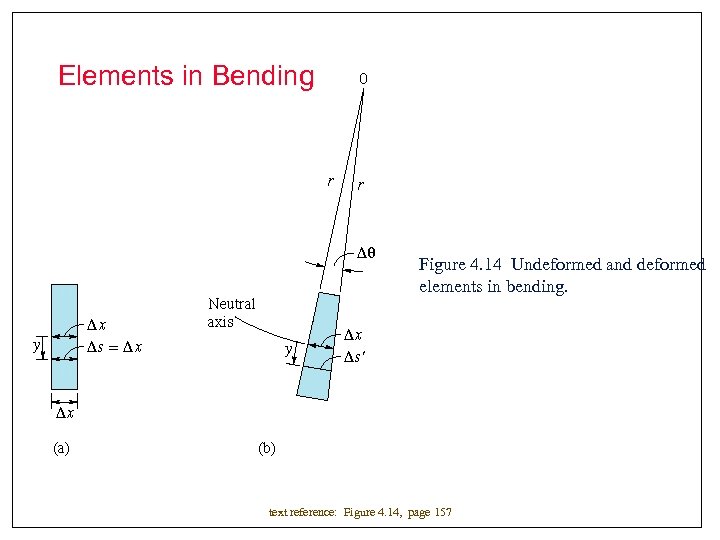
Elements in Bending Figure 4. 14 Undeformed and deformed elements in bending. text reference: Figure 4. 14, page 157
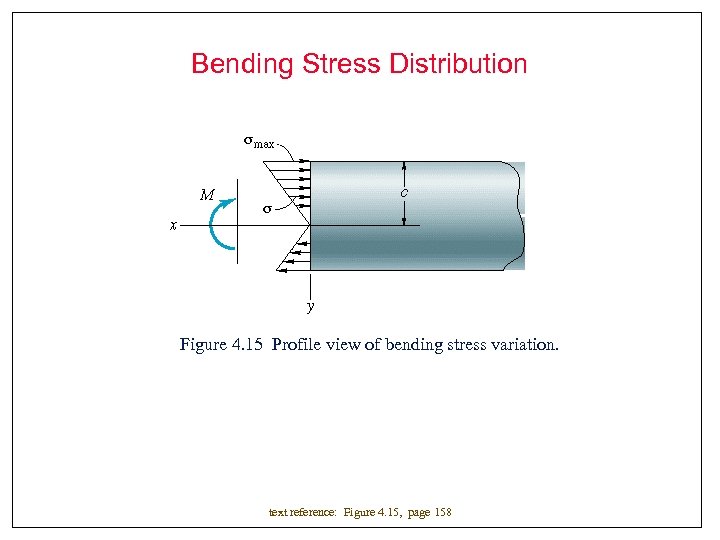
Bending Stress Distribution Figure 4. 15 Profile view of bending stress variation. text reference: Figure 4. 15, page 158
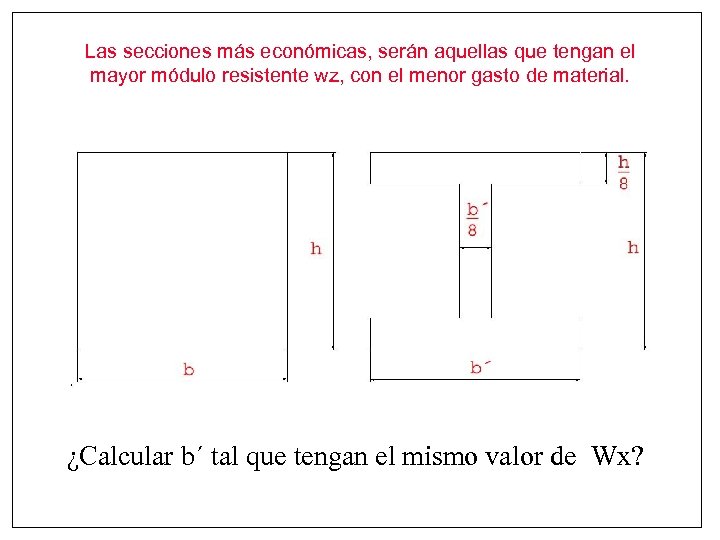
Las secciones más económicas, serán aquellas que tengan el mayor módulo resistente wz, con el menor gasto de material. ¿Calcular b´ tal que tengan el mismo valor de Wx?
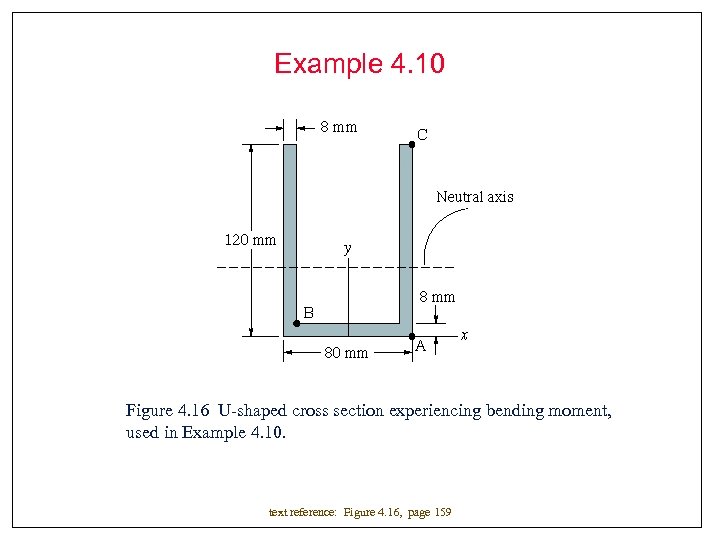
Example 4. 10 Figure 4. 16 U-shaped cross section experiencing bending moment, used in Example 4. 10. text reference: Figure 4. 16, page 159
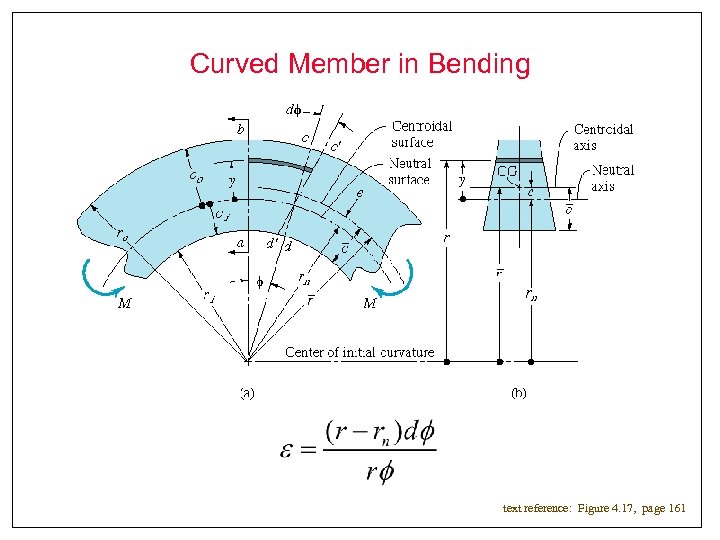
Curved Member in Bending text reference: Figure 4. 17, page 161

Curved Member in Bending Condición: sumatorio de esfuerzos en el rn=0
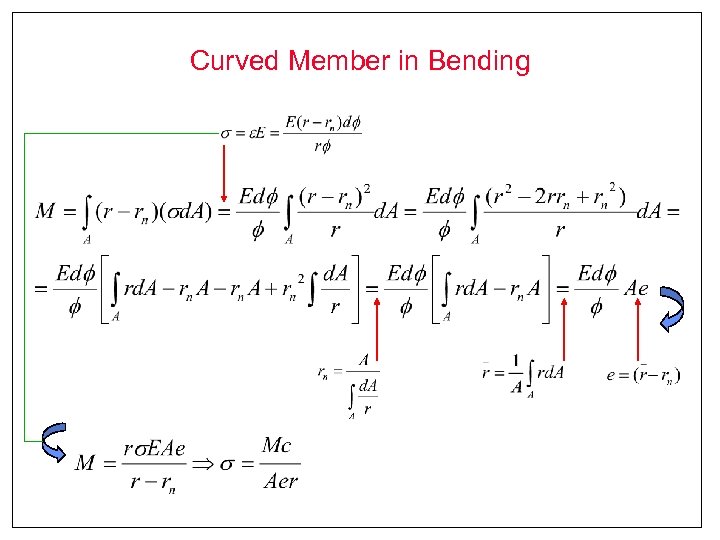
Curved Member in Bending
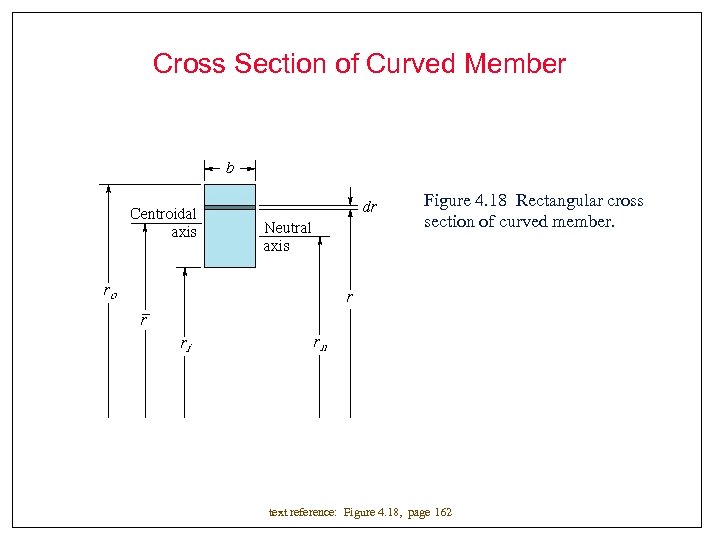
Cross Section of Curved Member Figure 4. 18 Rectangular cross section of curved member. text reference: Figure 4. 18, page 162
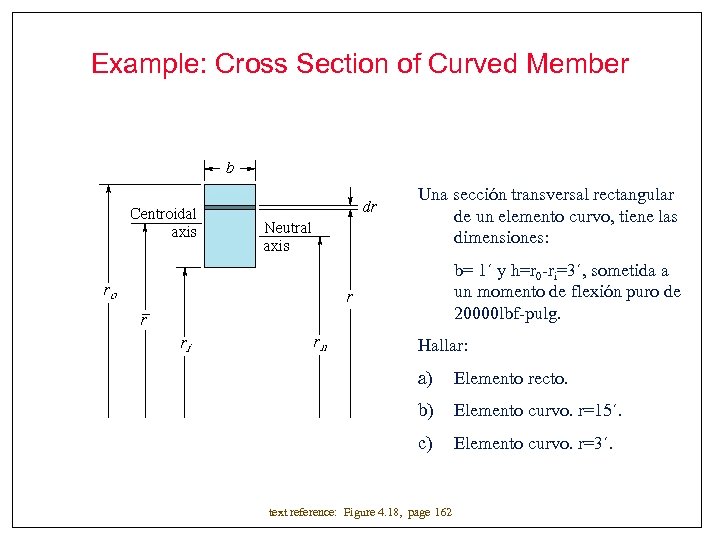
Example: Cross Section of Curved Member Una sección transversal rectangular de un elemento curvo, tiene las dimensiones: b= 1´ y h=r 0 -ri=3´, sometida a un momento de flexión puro de 20000 lbf-pulg. Hallar: a) Elemento recto. b) Elemento curvo. r=15´. c) Elemento curvo. r=3´. text reference: Figure 4. 18, page 162
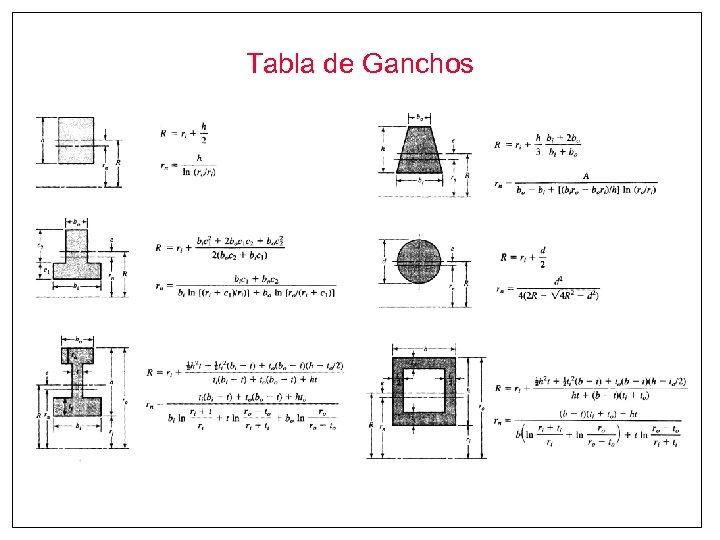
Tabla de Ganchos

Example: Cross Section of Curved Member Una sección trapezoidal de un elemento curvo, tiene las dimensiones: ri=10 cm F= 125 kg Tadm=1380 Kg/cm 2 Hallar: valor de a. text reference: Figure 4. 18, page 162
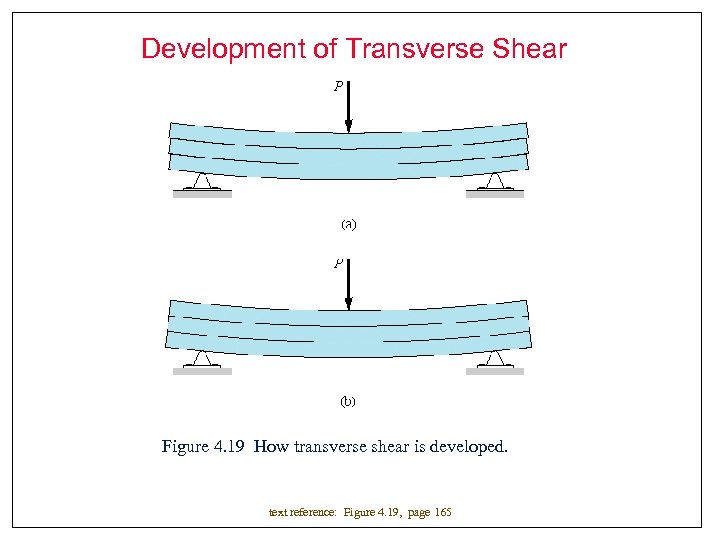
Development of Transverse Shear Figure 4. 19 How transverse shear is developed. text reference: Figure 4. 19, page 165
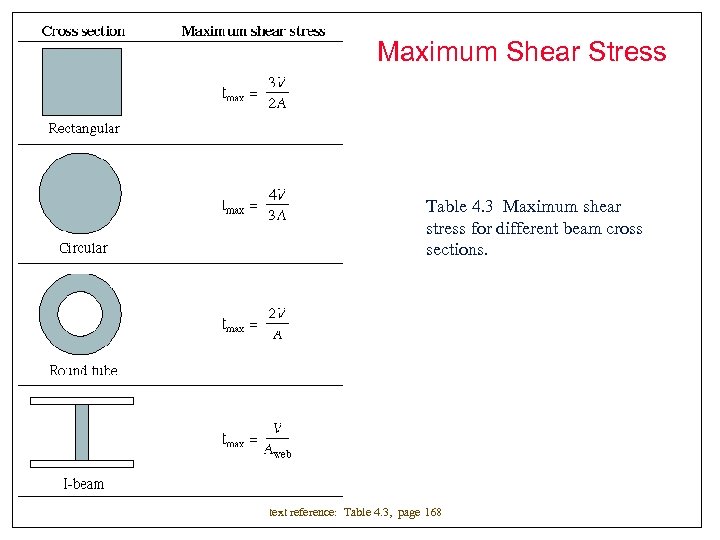
Maximum Shear Stress Table 4. 3 Maximum shear stress for different beam cross sections. text reference: Table 4. 3, page 168
2b5d3858ba787c2ae154b2376134aef6.ppt