БИ x КОМБИНАТОРИКА А 2 2 2018 Тема

БИ x , КОМБИНАТОРИКА А

2/2/2018 Тема № 9. Введение в комбинаторику «Число, место и комбинация – три взаимно перекрещивающиеся, но отличные сферы мышления, к которым можно отнести все математические идеи» . Дж. Сильвестр МБОУ г. Иркутска лицей ИГУ, ligu. edu 38. ru Лавлинский М. В. , Lavlinski. MV@mail. ru

I. Комбинаторика - Наука изучающая, комбинации, которые можно составить из заданных объектов (От лат. «combinare» – «сочетать» , «соединять» ) Г. В. Лейбниц – ввёл термин «комбинаторика» «Об искусстве комбинаторики» (1666 г. ) Г. В. Лейбниц (1646 - 1716) Комбинаторные задачи (КЗ) – задачи, направленные на подсчет числа комбинаций Методы решения КЗ: 1) Перебор вариантов 2) Правило умножения 3) Применение комбинаторных формул

II. Перебор вариантов Задача № 1. Сколько четных двузначных чисел можно составить из цифр: 0, 1, 2, 4, 5, 9? Решение: 10 20 40 50 90 12 22 42 52 92 14 24 44 54 94 Ответ: 15

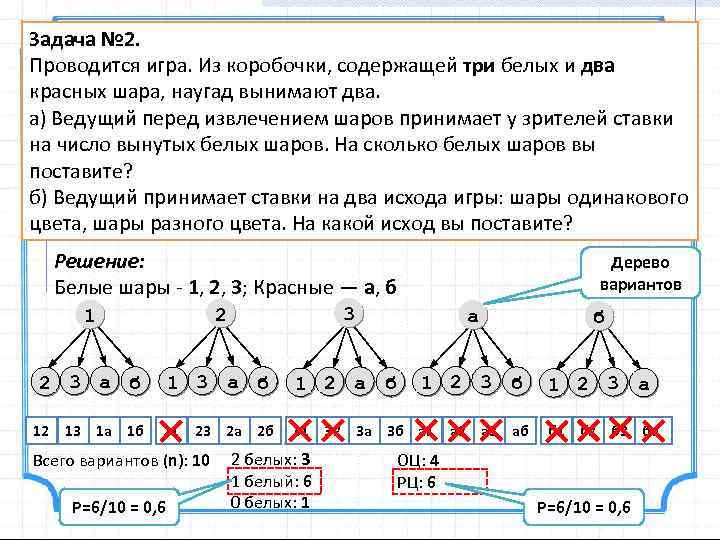
Задача № 2. Проводится игра. Из коробочки, содержащей три белых и два красных шара, наугад вынимают два. а) Ведущий перед извлечением шаров принимает у зрителей ставки на число вынутых белых шаров. На сколько белых шаров вы поставите? б) Ведущий принимает ставки на два исхода игры: шары одинакового цвета, шары разного цвета. На какой исход вы поставите? Решение: Белые шары - 1, 2, 3; Красные — а, б Дерево вариантов 1 2 3 а б 1 2 3 б 1 2 3 а 12 13 1 а 1 б 21 23 2 а 2 б 31 32 3 а 3 б а 1 а 2 а 3 аб Всего вариантов (n): 10 P=6/10 = 0, 6 2 белых: 3 1 белый: 6 0 белых: 1 б 2 б 3 ба ОЦ: 4 РЦ: 6 P=6/10 = 0, 6

III. Правило умножения Если элемент А может быть выбран k 1 способами, а элемент В – k 2 способами, то выбор «А и В» может быть осуществлен k 1 k 2 способами Задача № 4. Задача № 3. Сколько различных двузначных чисел кратных 5 двузначных чисел можно составить из цифр: 1, 3, 5, 7, 9? Решение: Дано: N = k 1 k 2 k 1 = 5 k 2 = 1 k 2 = 5 N = 5 5 = 25 N=5 1=5 Найти: N-? Ответ: 25 Найти: N-? Ответ: 5

Задача № 5. Сколько существует способов занять 1 -ое, 2 -ое и 3 -е места на чемпионате по футболу, в котором участвуют а) 10 команд Решение: N = 10 9 8 = 720 б) 11 команд? Решение: N = 11 10 9 = 990

Задача № 6. Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг. а)Сколько всего стран могут использовать такую символику? Решение: N=4 3 2 1 = 24 б) Сколько стран могут использовать такую символику с синей и красной полосами, расположенными рядом? Решение: N = 2 (3 2 1) = 12 (т. к. возможно синяя-красная, или красная-синяя)

Задача № 6. Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг. в) Сколько всего стран могут использовать такую символику с нижней белой полосой? Решение: N=3 2 1=6 г) Сколько стран могут использовать такую символику с верхней белой полосой? Решение: N=3 2 1=6

Задача № 7. Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы Миша и Оля оказались рядом? Решение: Способ 1. См. задачу 6 Способ 2. k 1 = 6 (Способы посадить Мишу) k 2 = 1 или 2 (Способы посадить Олю рядом) Это зависит от того, куда мы посадили Мишу 1) Миша сидит на краю N 1 = 2 1 4 3 2 1 = 48 способов 2) Миша сидит не на краю N 2 = 4 1 4 3 2 1 = 192 способа 3) N = 48 + 192 = 240 Ответ: 240

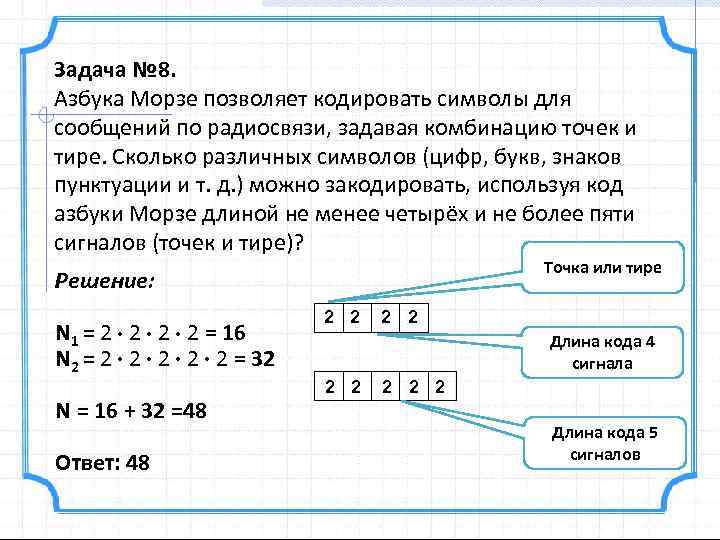
Задача № 8. Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т. д. ) можно закодировать, используя код азбуки Морзе длиной не менее четырёх и не более пяти сигналов (точек и тире)? Точка или тире Решение: N 1 = 2 2 = 16 N 2 = 2 2 2 = 32 N = 16 + 32 =48 Ответ: 48 2 2 Длина кода 4 сигнала 2 2 2 Длина кода 5 сигналов

Задача № 9. Какое наименьшее число символов должно быть в алфавите, чтобы при помощи всевозможных трехбуквенных слов, состоящих из символов данного алфавита, можно было передать не менее 9 различных сообщений? Решение: N= х х х ≥ 9 х=3 Ответ: 3 х х х 3 -ех буквенные слова

Задача № 10. Каждая ячейка памяти компьютера, работающего в троичной системе счисления, может принимать три различных значения (-1, 0, 1). Для хранения некоторой величины отвели 4 ячейки памяти. Сколько различных значений может принимать эта величина? Решение: N = 3 3 = 81 Ответ: 81 3 3

IV. Формула M - мощность алфавита –количество символов в этом алфавите Q - количество всех возможных «слов» (символьных цепочек) N – длина «слов» (без учета смысла)

Дискретная математика, 9 класс 2/2/2018 Домашнее задание 1. Конспект 2. СР «Введение в комбинаторику» 3. « 9_[ДЗ]Введение в комбинаторику. doc» МБОУ г. Иркутска лицей ИГУ, ligu. edu 38. ru