Безрукова Т В Лекция 1 Комплексный чертеж точки

Безрукова Т. В. Лекция 1 «Комплексный чертеж точки, прямой» 2012 1

ПЛАН ЛЕКЦИИ 1. a. b. c. 2. 3. Метод проекций: центральное проецирование; параллельное проецирование; ортогональное проецирование. Комплексный чертеж точки Комплексный чертеж прямой Лекция: «Комплексный чертеж точки, прямой» 2

Начертательная геометрия представляет собой раздел геометрии, в котором пространственные формы предметов и их геометрические свойства изучаются при помощи изображений на плоскости, т. е. чертежей. Требования к чертежу: Обратимость – по нему точно возможно воспроизвести форму и размеры изображаемого предмета. Простота его графического выполнения. Графические построения должны давать достаточно точные решения. Содержание курса начертательной геометрии: 1. Изучение способов построения изображений (чертежей) пространственных фигур на плоскости. 2. Изучение способов решения на чертеже задач, связанных с геометрическими образами и их пространственным взаимным расположением. 3. Развитие пространственного мышления, т. е. по плоскому изображению образа мысленно уметь представить себе их объемную форму и взаимное расположение. Геометрические образы – это точка, линия, поверхность, плоскость. При этом в НГ рассматриваются линии, а не часть пространства ими ограниченные (например, окружность, а не круг) и поверхности, не имеющие толщины и оснований, а не геометрические тела. 3

Метод проекций Для изображения предметов на плоскости используют метод проецирования. ПРОЕЦИРОВАНИЕМ Лекция: «Комплексный чертеж точки, прямой» 4

Метод проекций ДЛЯ ПОСТРОЕНИЯ ПРОЕКЦИИ КАКОЙЛИБО ФИГУРЫ НЕОБХОДИМО ЧЕРЕЗ ЕЕ ХАРАКТЕРНЫЕ ТОЧКИ ПРОВЕСТИ ПРОЕЦИРУЮЩИЕ ЛУЧИ ДО ПЕРЕСЕЧЕНИЯ ИХ С ПЛОСКОСТЬЮ ПРОЕКЦИЙ. ПОЛУЧЕННЫЕ ТАКИМ ОБРАЗОМ ТОЧКИ СОЕДИНЯЮТ ПРЯМЫМИ ИЛИ КРИВЫМИ ЛИНИЯМИ. Лекция: «Комплексный чертеж точки, прямой» 5

Метод проекций ЦЕНТРАЛЬНЫЕ ПАРАЛЛЕЛЬНЫЕ. ЦЕНТРАЛЬНОЙ ЦЕНТРАЛЬНЫМ Лекция: «Комплексный чертеж точки, прямой» 6

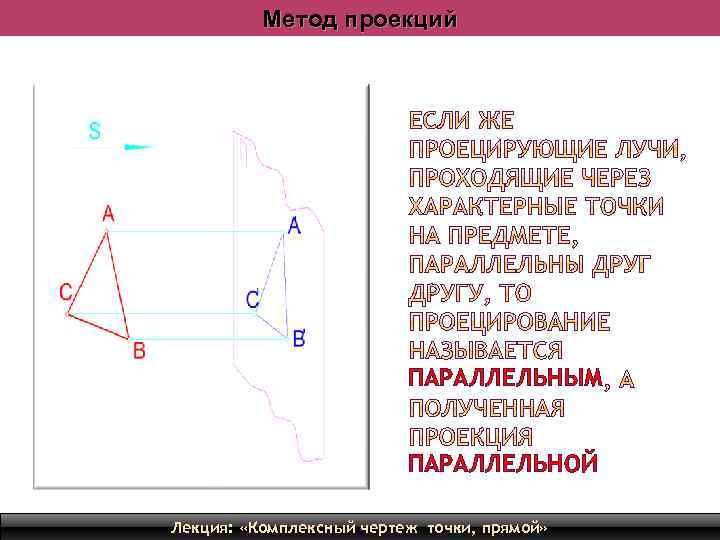
Метод проекций ПАРАЛЛЕЛЬНЫМ ПАРАЛЛЕЛЬНОЙ Лекция: «Комплексный чертеж точки, прямой» 7

Комплексный чертеж точки КОМПЛЕКСНЫМ, Лекция: «Комплексный чертеж точки, прямой»

Центральное проецирование: 1. Точка проецируется в точку. 2. Прямая проецируется в прямую. Исключение: если направление проецирующего луча совпадает с самой прямой, то проекцией прямой будет точка. 3. Если точка принадлежит прямой, то проекция точки принадлежит проекции прямой. 9

Параллельное проецирование сохраняет свойства центрального и обладает дополнительными свойствами: 4. Если прямые параллельны в пространстве, то их проекции параллельны. 5. Отношение отрезков прямой равно отношению проекций этих отрезков. 6. Отношение отрезков параллельных прямых равно отношению проекций этих отрезков. 7. Проекция геометрического образа по величине и форме не изменяется при параллельном переносе плоскости проекций. Ортогональному проецированию, помимо перечисленных выше, принадлежит еще одно свойство: 8. Проекция отрезка не может быть больше самого отрезка. 10

П 1 – горизонтальная плоскость проекций; П 2 - фронтальная плоскость проекций; П 3 – профильная плоскость проекций. А 1, А 2, А 3 - горизонтальная, фронтальная и профильная проекции точки А. h – высота точки А; f – глубина точки А; P – широта точки А. Лекция: «Комплексный чертеж точки, прямой» 11

Комплексный чертеж точки Лекция: «Комплексный чертеж точки, прямой» 12

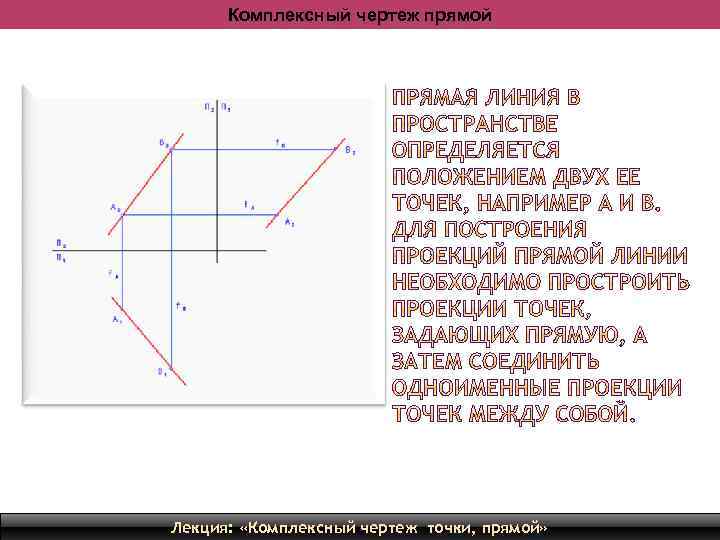
Комплексный чертеж прямой Лекция: «Комплексный чертеж точки, прямой» 13

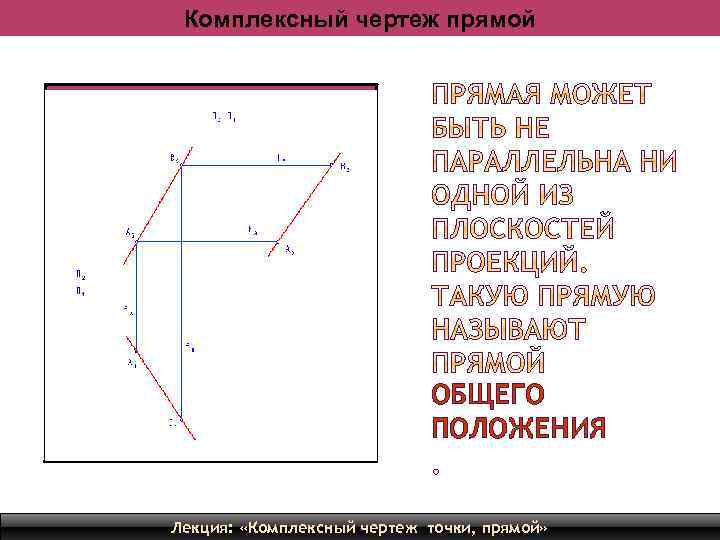
Комплексный чертеж прямой ОБЩЕГО ПОЛОЖЕНИЯ Лекция: «Комплексный чертеж точки, прямой» 14

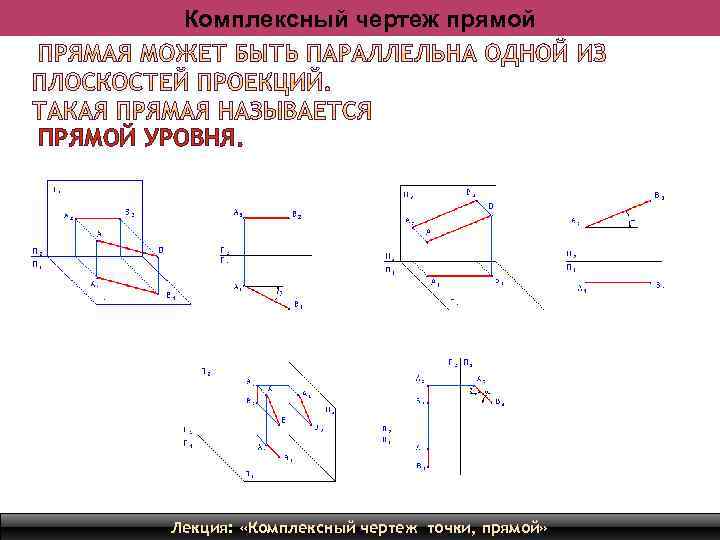
Комплексный чертеж прямой ПРЯМОЙ УРОВНЯ. Лекция: «Комплексный чертеж точки, прямой» 15

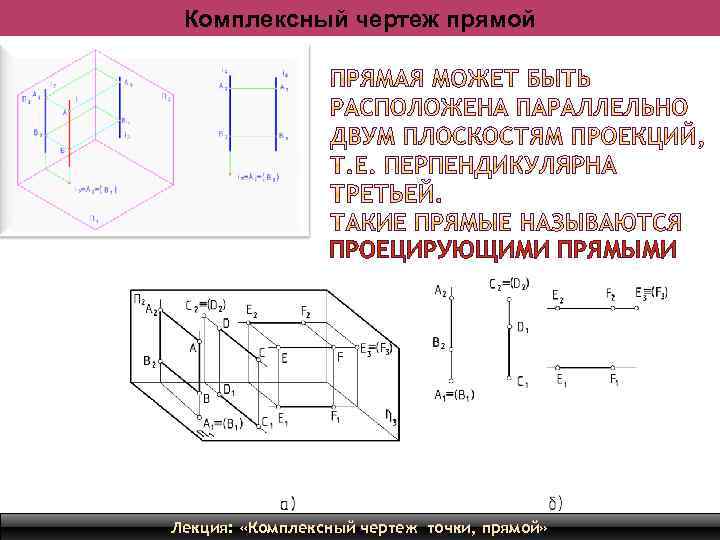
Комплексный чертеж прямой ПРОЕЦИРУЮЩИМИ ПРЯМЫМИ Лекция: «Комплексный чертеж точки, прямой» 16

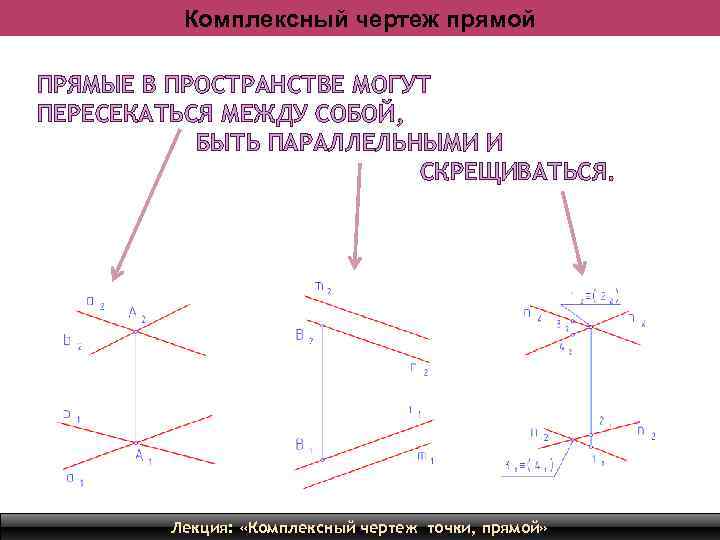
Комплексный чертеж прямой ПРЯМЫЕ В ПРОСТРАНСТВЕ МОГУТ ПЕРЕСЕКАТЬСЯ МЕЖДУ СОБОЙ, БЫТЬ ПАРАЛЛЕЛЬНЫМИ И СКРЕЩИВАТЬСЯ. Лекция: «Комплексный чертеж точки, прямой» 17

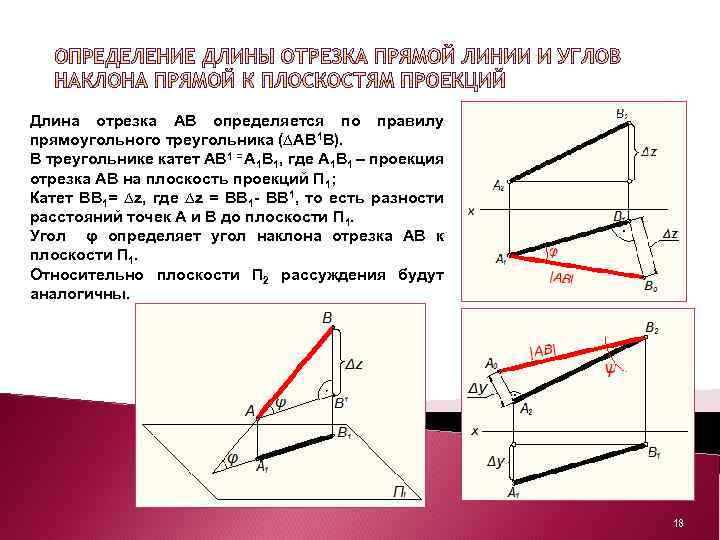
Длина отрезка АВ определяется по правилу прямоугольного треугольника (∆АВ 1 В). В треугольнике катет АВ 1 = А 1 В 1, где А 1 В 1 – проекция отрезка АВ на плоскость проекций П 1; Катет ВВ 1= ∆z, где ∆z = ВВ 1 - ВВ 1, то есть разности расстояний точек А и В до плоскости П 1. Угол φ определяет угол наклона отрезка АВ к плоскости П 1. Относительно плоскости П 2 рассуждения будут аналогичны. 18

Следом прямой линии называется точка, в которой прямая пересекается с плоскостью проекций. Так как след прямой принадлежит одной из плоскостей проекций, то одна из координат каждого следа должна быть равна нулю. Правило построения следов на эпюре Горизонтальный след М – точка пересечения прямой с 1. Для П , ее координата Z = 0. плоскостью построения горизонтального следа 1 M М прямой необходимо пересечения прямой Фронтальный след N (y. N = 0) – точка продолжить ее с фронтальную проекцию до пересечения плоскостью П 2. Профильный след и (x. Tэтой пересечение с плоскостью П 3. с осью 0 x Т в =0) – точке восстановить к оси перпендикуляр до пересечения с горизонтальной проекцией прямой. 2. Для построения фронтального следа N прямой необходимо продолжить ее горизонтальную проекцию до пересечения с осью 0 x и в этой точке восстановить к оси перпендикуляр до пересечения с фронтальной проекцией прямой. Следы прямой определяют точки , в которых прямая переходит из одной четверти в другую, позволяют отмечать видимость. 19

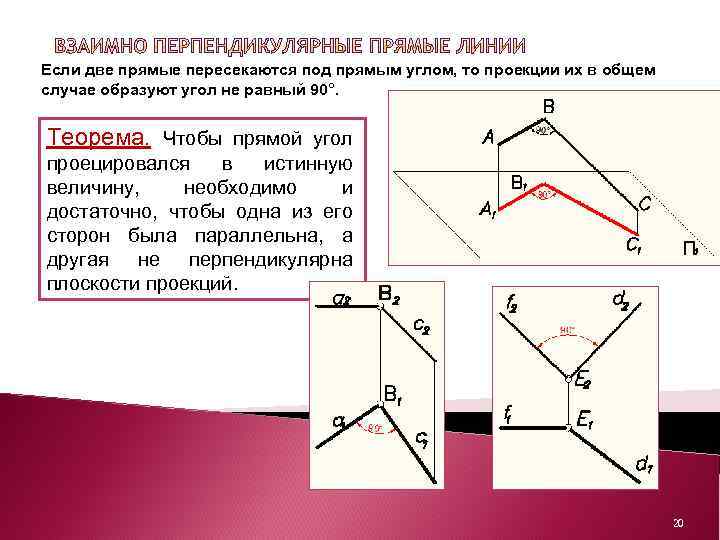
Если две прямые пересекаются под прямым углом, то проекции их в общем случае образуют угол не равный 90°. Теорема. Чтобы прямой угол проецировался в истинную величину, необходимо и достаточно, чтобы одна из его сторон была параллельна, а другая не перпендикулярна плоскости проекций. 20

При проецировании отрезка AB на П 1 получим отрезок A 1 B 1, при проецировании на П 2 – A 2 B 2. На рис. показан комплексный чертеж отрезка AB. Поскольку отношение длин отрезков, лежащих на одной прямой, при проецировании не меняется, то для деления отрезка в данном отношении достаточно разделить в этом отношении одну проекцию отрезка, и это полностью определит точку деления. На рис. показано построение точки C, делящей отрезок AB в отношении AC : CB = 3 : 2. На основе теоремы Фалеса в отношении 3 : 2 делим горизонтальную проекцию отрезка, т. е. A 1 C 1 : C 1 B 1 = 3 : 2. Так находим точку C 1. Затем по линии проекционной связи находим C 2. Точка C 2 делит фронтальную проекцию отрезка в том же отношении A 2 C 2 : C 2 B 2 = 3 : 2 (по теореме Фалеса, так как линии проекционной связи всех точек параллельны). На рис. последовательность построений показана стрелкой на линии проекционной связи – сначала строится C 1, а затем C 2.