Beyond Wavelets and JPEG 2000 Tony Lin Peking

Beyond Wavelets and JPEG 2000 Tony Lin Peking University, Beijing, China Dec. 17, 2004 1

Outline n n n Wavelets and JPEG 2000: A brief review Beyond wavelets and JPEG 2000 My exploration q q q n Directional wavelet construction Adaptive wavelet selection Inter-subband transform Outlook 2

References n Classical books on wavelets and subband q q q q q I. Daubechies, "Ten lectures on wavelets, " 1992. P. P. Vaidyanathan, "Multirate systems and filter banks, " 1992. C. K. Chui, An Introduction to Wavelets, 1992. Y. Meyer, “Wavelets: Algorithms and Applications, ” 1993. Vetterli and J. Kovacevic, "Wavelets and subband coding, " 1995. G. Strang and T. Nguyen, "Wavelet and filter banks, " 1996. C. K. Chui, Wavelets: A mathematical tool for signal analysis, 1997. C. S. Burrus, R. A. Gopinath, and H. Guo, "Introduction to wavelets and wavelet transforms: A primer, " 1998. S. Mallat, "A wavelet tour of signal processing, " second edition, 1998. 3

References n Beyond q q q David Donoho, “Beyond Wavelets, ” ten lectures, 2000. Book: G. Welland ed. , Beyond wavelets, 2003. Martin Vetterli, "Wavelets, approximation and compression: Beyond JPEG 2000, " San Diego, Aug. 2003. Martin Vetterli, "Fourier, wavelets and beyond: the search for good bases for images, " Singapore, Oct. 2004. M. N. Do, "Beyond wavelets: Directional multiresolution image representation, " 2003. 4

References n Beyond (cont. ) q q q David Donoho, "Data compression and harmonic analysis, " IEEE Trans. Info Theory, 1998. Martin Vetterli, "Wavelets, approximation, and compression, " IEEE Sig. Proc. Mag. , Sept. 2001. E. L. Pennec, S. Mallat, "Sparse geometric image representations with bandelets, " July 2003. 5

References n JPEG 2000 q q Book: D. Taubman & M. Marcellin, “JPEG 2000: Image compression fundamentals, standards and pratice, ” 2002. D. Taubman, “High performance scalable image compression with EBCOT, ” IEEE Trans. Image Proc. , 2000. Jin Li, “Image compression: mechanics of JPEG 2000, ” 2001. M. Adams, “The JPEG-2000 still image compression standard, ” 2002. 6

Main Contributors n Wavelets (Mathematics) q n Subband (EE) q n Daubechies, Mallat, Meyer, Donoho, Strang, Sweldens, … Vaidyanathan, Vetterli, … Image Compression (EE) q Shapiro (EZW), Said&Pearlman (SPIHT), Taubman (EBCOT), Jin Li (R-D optimization) 7

Part I: Wavelets and JPEG 2000: A brief review "Who controls the past, ran the Party slogan, controls the future; who controls the present, controls the past. " -- George Orwell, 1984. 8

Wavelets n n n n n Then dulcet music swelled Concordant with the life-strings of the soul; It throbbed in sweet and languid beatings there, Catching new life from transitory death; Like the vague sighings of a wind at even That wakes the wavelets of the slumbering sea. . . ---Percy Bysshe Shelley Queen Mab: A Philosophical Poem, with Notes, published by the author, London, 1813. This is given by The Oxford English Dictionary as one of the earliest instances of the word "wavelet". For an instance in current poetry in this generic sense, see Breath, by Natascha Bruckner. http: //www. math. uiowa. edu/~jorgen/shelleyquotesource. html 9

Wavelets = Wave + lets n Pure Mathematics q q q Algebra Geometry Analysis (mainly studying functions and operators) n Fourier, Harmonic, Wavelets 10

Why Wavelets Work? n n n Wavelet functions are those functions such that their integer translate and two-scale dilations, i. e. , f(2 mxn) for all integer m and n form a Riesz basis for the space of all square integrable functions ( L 2(R) ). Such functions provide a good basis for approximating signal and images. n -- From Ming-Jun Lai’s homepage Notes: q q Simple: Just do translation and dilations for f(x) Complete: Riesz basis for L 2(R) 11

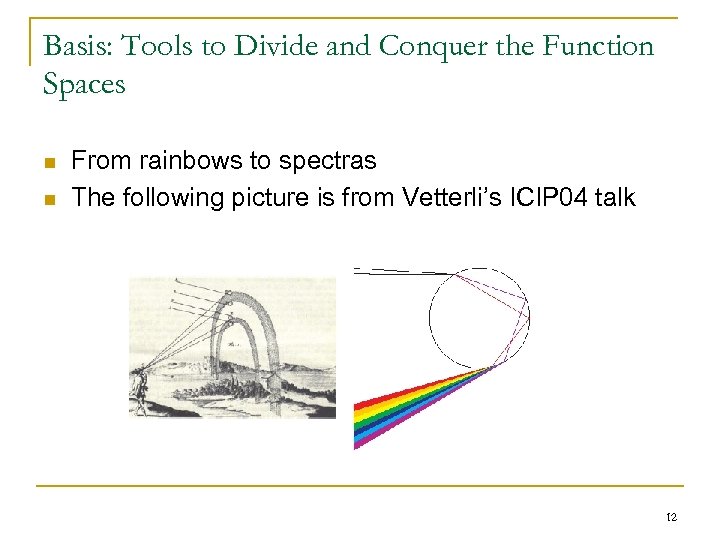
Basis: Tools to Divide and Conquer the Function Spaces n n From rainbows to spectras The following picture is from Vetterli’s ICIP 04 talk 12

Subband vs. Wavelets n n Wavelets allow the use of powerful mathematical theory in function analysis, so that many function properties can be studied and used. The values in DWT are fine-scale scaling function coefficients, rather than samples of some function. This specifies that the underlying continuous-valued functions are transformed. Wavelets involve both spatial and frequency considerations. G. Davis and A. Nosratinia, "Wavelet-Based Image Coding: An Overview", 1998. 13

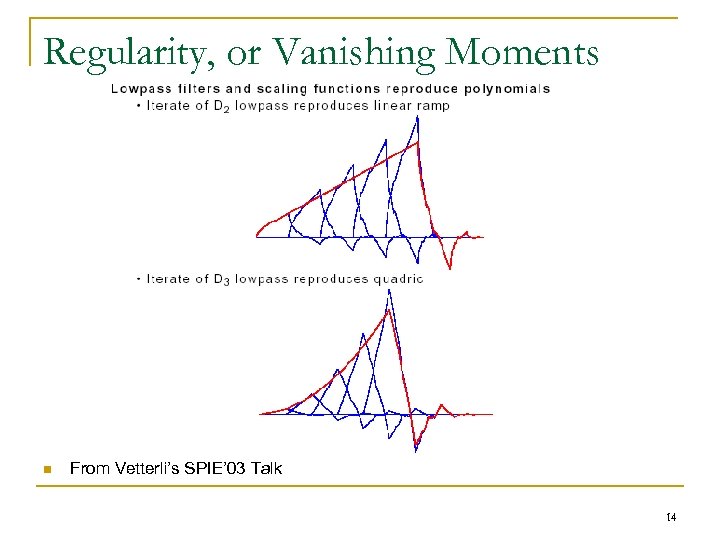
Regularity, or Vanishing Moments n From Vetterli’s SPIE’ 03 Talk 14

Orthogonal vs. Biorthogonal -- B. Usevitch, "A turorial on modern lossy wavelet image compression: foundations of JPEG 2000, " IEEE Trans. Sig. Proc. Mag. , 2001. n Orthogonal: q q n Energy conservation: simplifies the designing wavelet-based image coder Drawback: Coefficient expansion (e. g. , 8 (input) + 4 (filter) = 12 (output) ). Worse for Multiple DWTs. Biorthogonal CDF 9/7 filter: q q Nearly orthogonal Solve the “coefficient expansion” problem. n n Symmetric extensions of the input data Filters are symmetric or antisymmetric 15

DWT Implementation: Convolution vs. Lifting n Daubechies and Sweldens, “Factoring wavelet transforms into lifting steps”, J. Fourier Anal. Appl. , 1998. 16

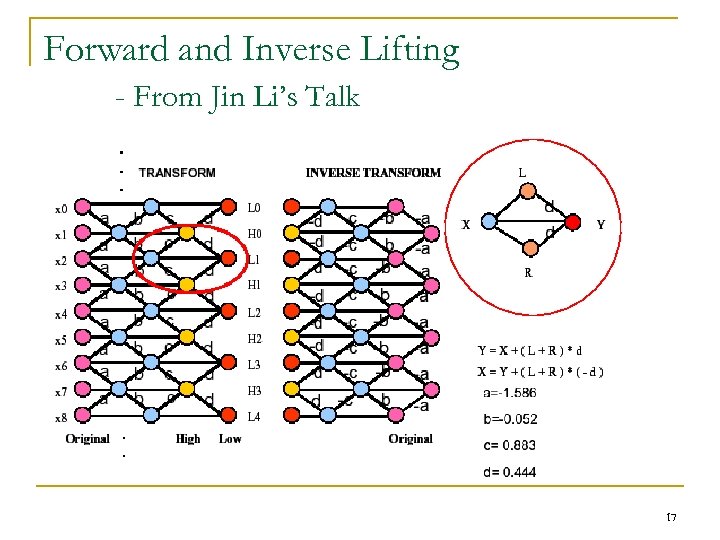
Forward and Inverse Lifting - From Jin Li’s Talk 17

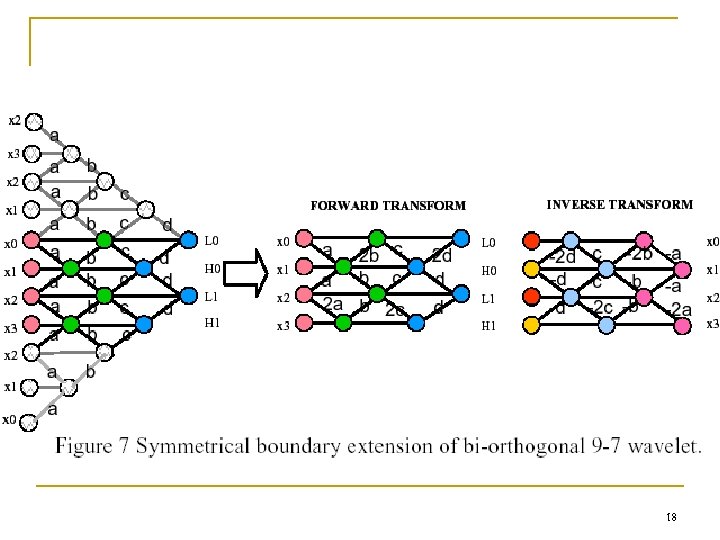
18

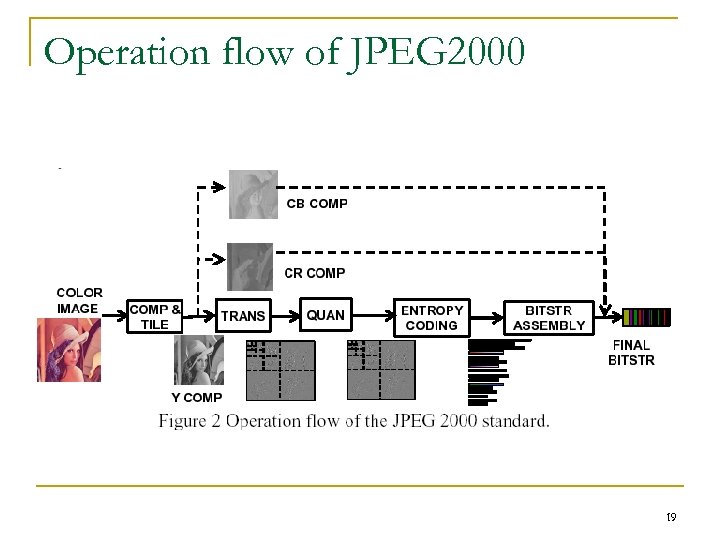
Operation flow of JPEG 2000 19

Secret 1 for the coding efficiency of JPEG 2000: -- Multiple levels of DWT LL block n Only a small portion of coefficients are needed to coded. n Why 5 -level decomposition? Because further decomposition can not improve the performance, since the LL block has been very small. n Divide and Conquer Five DWT decompositions of Barbara image 20

Secret 2 for the coding efficiency of JPEG 2000: -- EBCOT: Fractional bitplane coding and Multiple contexts to implement a high performance arithmetic coder n Divide and Conquer q q q Bitplane coding Three passes for each bitplane: Significance, refinement, cleanup Different contexts: Sig (LL+LH, HL, HH), Sign, Ref 21

Part II: Beyond wavelets and JPEG 2000 "My dream is to solve problems, with or without wavelets" -- Bruno Torresani, 1995 22

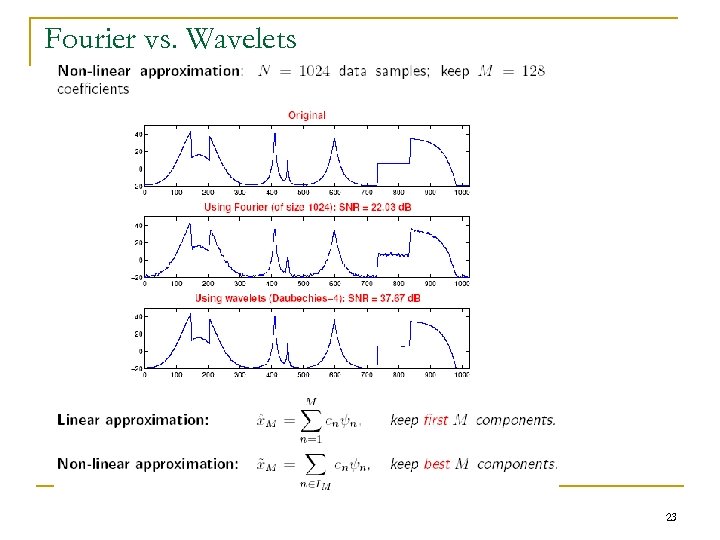
Fourier vs. Wavelets 23

The failure of Wavelets in 2 -D 24

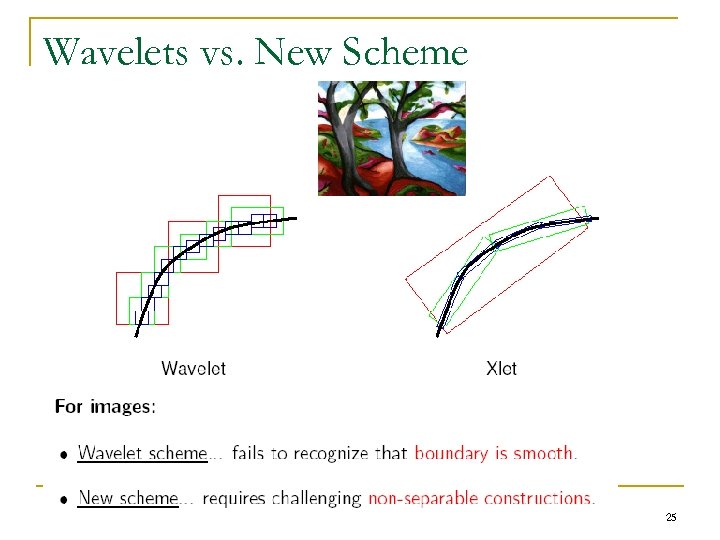
Wavelets vs. New Scheme 25

Curvelets: Breakthrough by Candes and Donoho, 1999 26

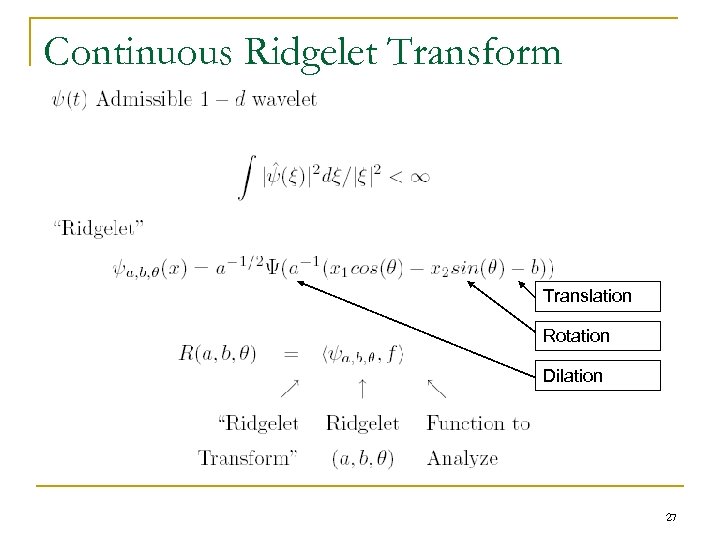
Continuous Ridgelet Transform Translation Rotation Dilation 27

Orthonormal Ridgelets 28

Curvelets: Combining wavelets and ridgelets 29

Curvelet Transform: An Example 30

Second Generation of Curvelets: Without Ridgelets, 2002 Dilation Rotation Translation 31

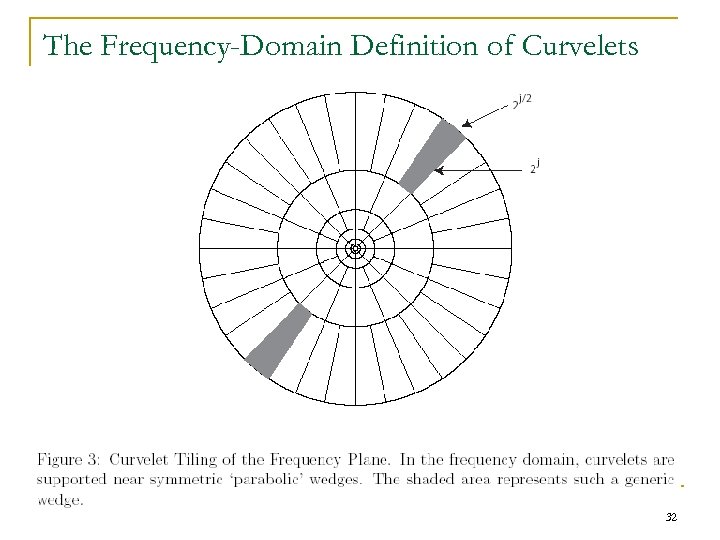
The Frequency-Domain Definition of Curvelets 32

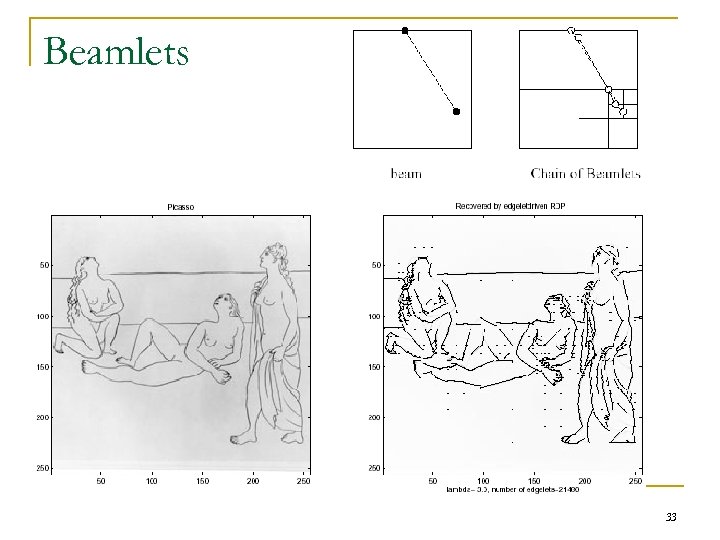
Beamlets 33

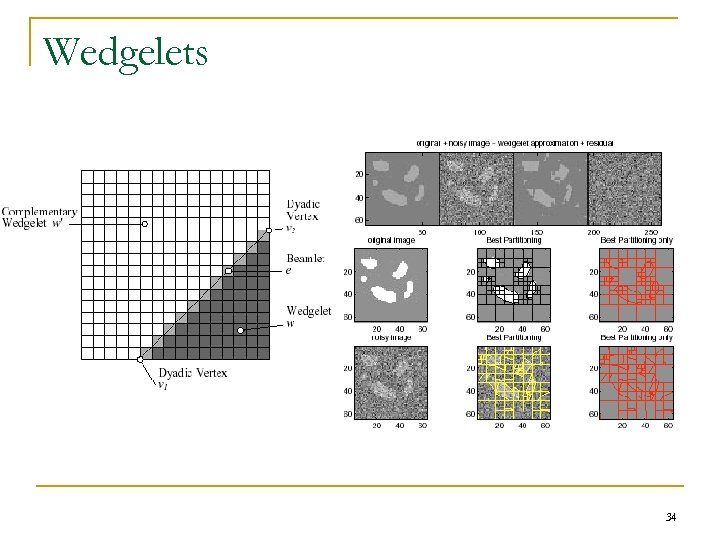
Wedgelets 34

Contourlets by M. Do and M. Vetterli 35

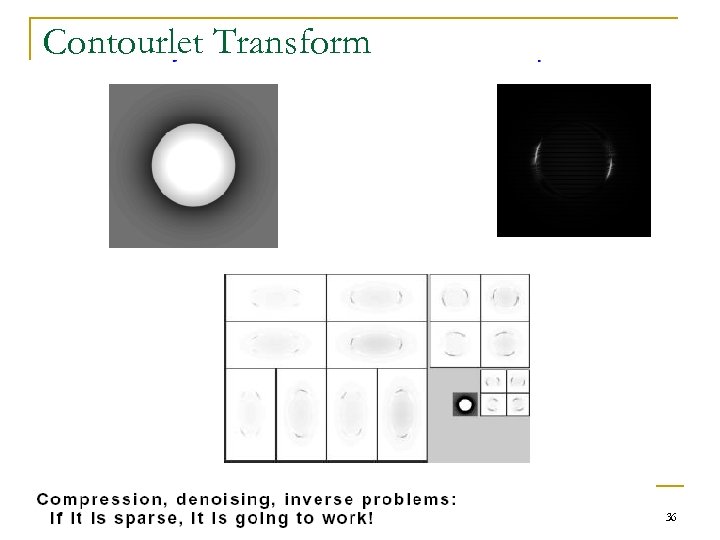
Contourlet Transform 36

Contourlet Transform (Cont. ) 37

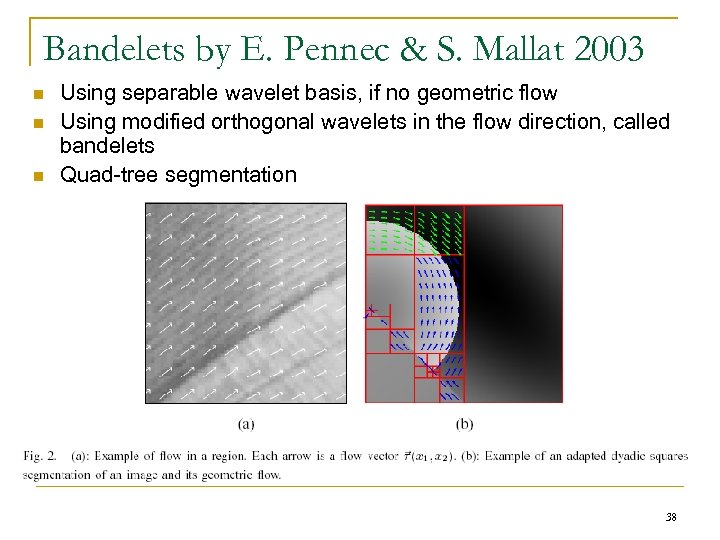
Bandelets by E. Pennec & S. Mallat 2003 n n n Using separable wavelet basis, if no geometric flow Using modified orthogonal wavelets in the flow direction, called bandelets Quad-tree segmentation 38

Example 1 39

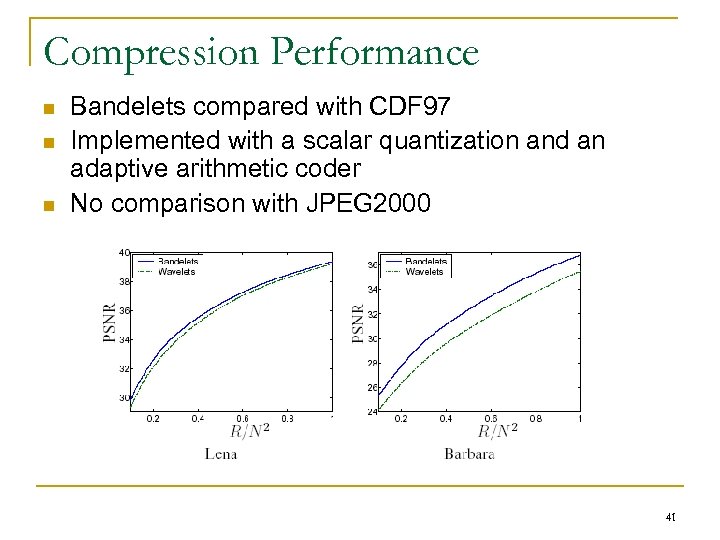
Example 2 40

Compression Performance n n n Bandelets compared with CDF 97 Implemented with a scalar quantization and an adaptive arithmetic coder No comparison with JPEG 2000 41

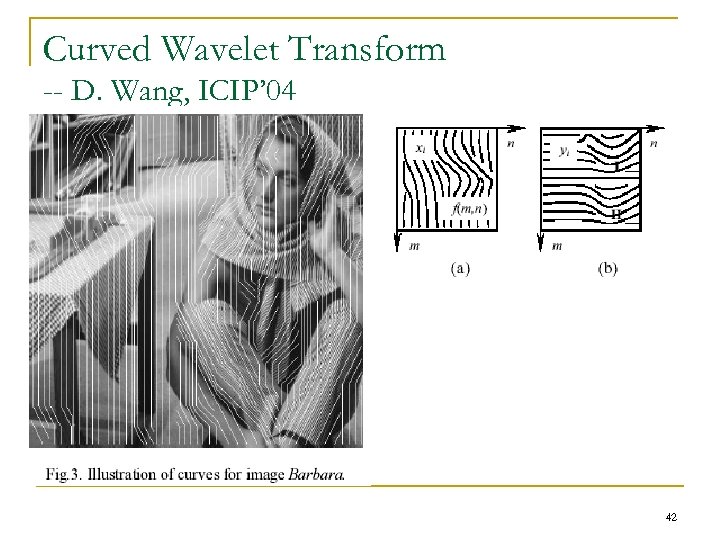
Curved Wavelet Transform -- D. Wang, ICIP’ 04 42

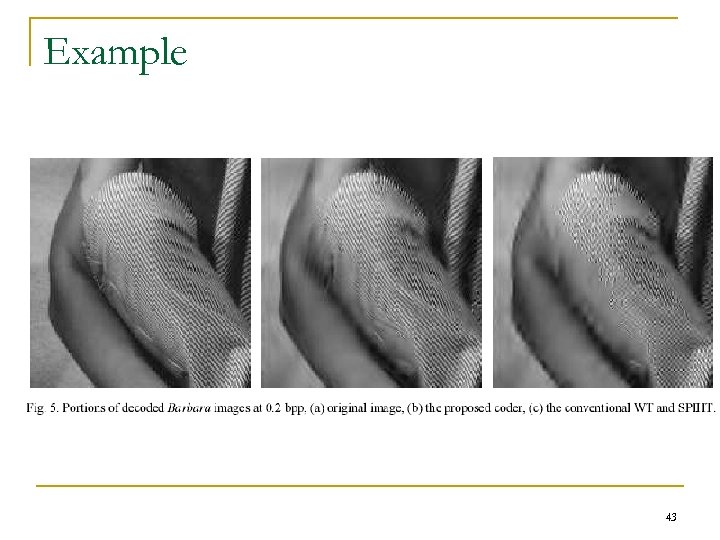
Example 43

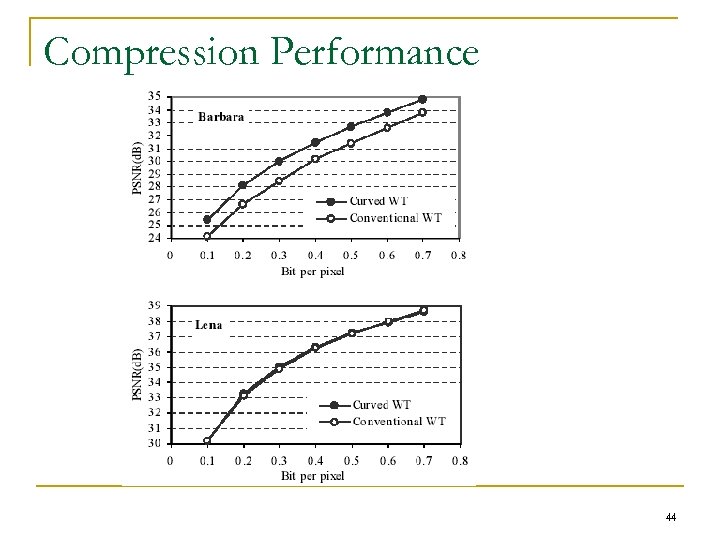
Compression Performance 44

Part III: My exploration: 1. Directional wavelet construction 2. Adaptive wavelet selection 3. Inter-subband transform "There have been too many pictures of Lena, and too many bad wavelet sessions at meetings. " -- M. Vetterli, 1995. "If you steal from one author, it's plagiarism; if you steal from many, it's research" -- Wilson Mizner, 1953. 45

Directional wavelet construction n n Find a 2 -D wavelet function such that their translations, dilations, and rotations form a basis for the space of all square integrable functions ( L 2(R) ). Build new multiresolution theory Build fast algorithms to do multiscale transforms How ? If succeed, it would be similar to the curvelets by Candes. 46

Adaptive Wavelet Selection n n Different wavelets have different support lengths, vanishing moments, and smoothness Longer and smoother wavelets for smooth image regions Shorter and more rugged wavelets for edge regions Adaptively select the best wavelet basis 47

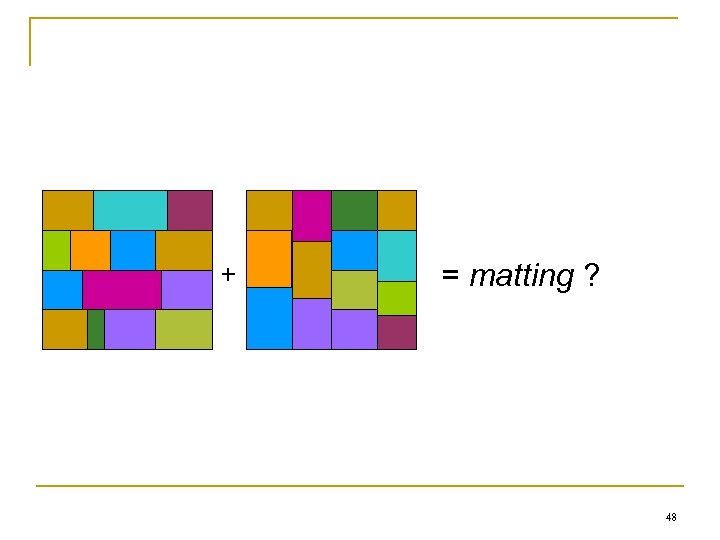
+ = matting ? 48

Shortcomings n n Difficult to find a measure to evaluate which wavelet basis is better Big overhead q q n Segmentation information The wavelet basis used in each segments Solutions 49

Further Transforms in Wavelet Domain n Curvelets, Contourlets, and Bandelets are new basis to approximate the ideal transform Wavelets are far from the ideal basis, but they are on the midway Further transforms in the wavelet domain can be benefited by the existing good properties offered by DWT 50

Inter-subband transform n n n EBCOT or JPEG 2000 uses neighbor coefficients to predict the current values EZW or SPIHT uses cross-scale correlations to do prediction Wavelet packets do further decomposition in each subband to reduce correlation …… How about the inter-subband transform that push the energy into the first or the second subbands ? 51

PCA for the three subbands (LH, HL, HH) n n n Programming with Matlab and VC+J 2000 codec Found that the PCA transform matrix is very close to Identity matrix Sometimes it provide slightly better performance than JPEG 2000, but it is not always 52

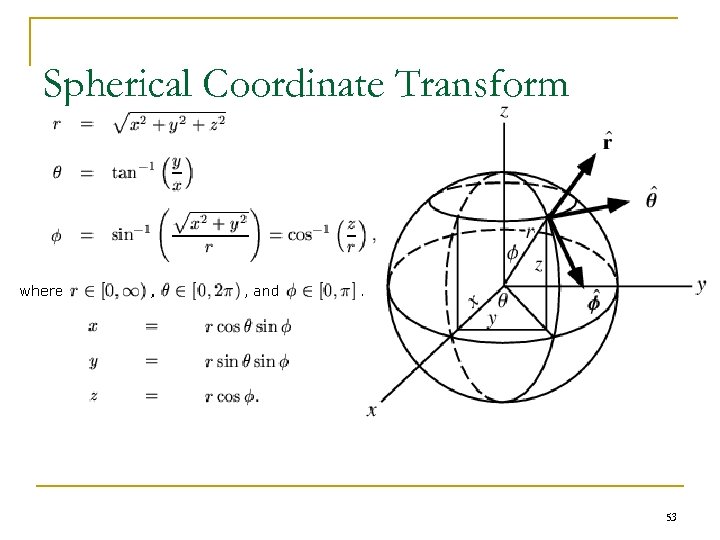
Spherical Coordinate Transform 53

Example 54

Shortcomings n n Spherical approximation Hard to design the rate-distortion allocation for the two angular subbands, because they depend on the R subband 55

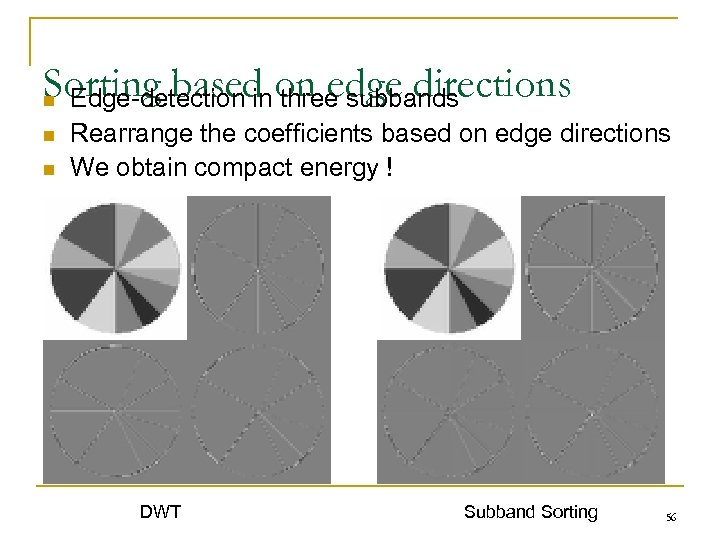
Sorting based on edge directions n Edge-detection in three subbands n n Rearrange the coefficients based on edge directions We obtain compact energy ! DWT Subband Sorting 56

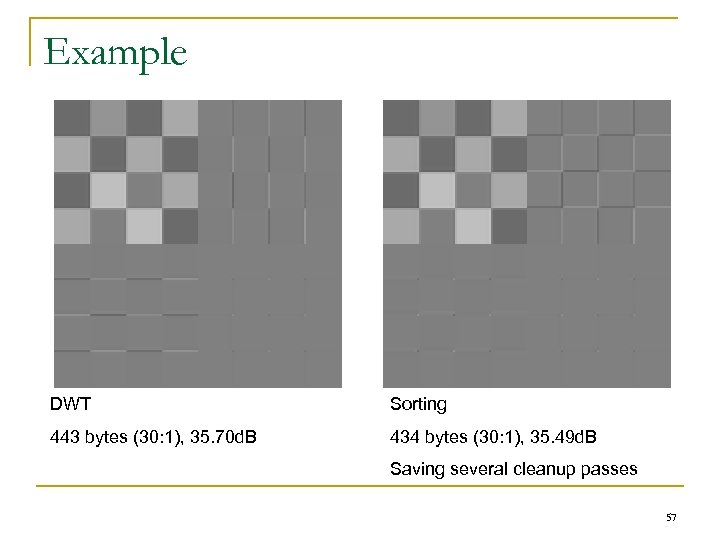
Example DWT Sorting 443 bytes (30: 1), 35. 70 d. B 434 bytes (30: 1), 35. 49 d. B Saving several cleanup passes 57

Part IV: Outlook "Predicting is hard, especially about the future. " -- Victor Borge, quoted by Philip Kotler. 58

Wish lists for next-generation basis n n n n Multiresolution or Multiscale Localization in both space and frequency Critical sampling: no coefficient expansion Easily control the filter length, smoothness, vanishing moments, and symmetry Directionality Anisotropy: spheres, ellipses, needles Adaptive basis 59

Over n There is a long way to go beyond wavelets and JPEG 2000 … n Questions 60