Глава 4-4-2.ppt
- Количество слайдов: 46

Бесконечно малые и бесконечно большие функции

О п р е д е л е н и е 1. Функция у = f (x) называется бесконечно малой (Б. М. Ф. ) n при х а, n если ее предел равен нулю n
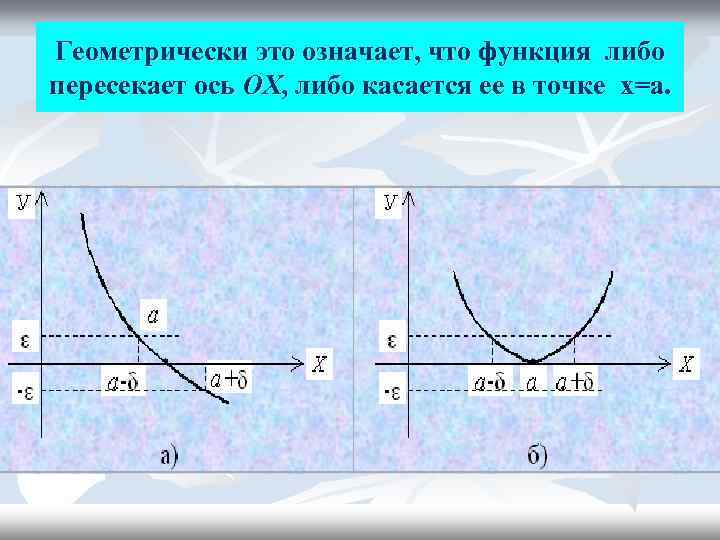
Геометрически это означает, что функция либо пересекает ось ОХ, либо касается ее в точке х=а.

О п р е д е л е н и е 2. n n n Функция у = f (x) называется бесконечно малой величиной при х , если для каждого положительного сколь угодно малого числа найдется сколь угодно большое положительное число N( ) такое, что для всех х, удовлетворяющих неравенству lxl >N будет выполняться неравенство





Свойства бесконечно малых и бесконечно больших функций и связь между ними



Связь бесконечно малой и бесконечно большой функций

Величина, обратная бесконечно малой величине, есть величина бесконечно большая, и наоборот, величина, обратная бесконечно большой величине, есть величина бесконечно малая.



Вычисление пределов, когда предел числителя и предел знаменателя равны нулю




П р а в и л о 2. n Чтобы найти предел дроби, содержащий иррациональные выражения в случае, когда пределы числителя и знаменателя равны нулю, надо перенести иррациональность из числителя в знаменатель, или наоборот. После этого следует сделать преобразования и перейти к пределу, используя известные формулы:



Раскрытие неопределенностей

П р а в и л о 1. n n Если при вычислении предела, представляющего собой разность двух функций, получим неопределенность то чтобы избавиться от неопределенности, надо, или привести функции к общему знаменателю, или, при наличии иррациональности, перенести ее из числителя в знаменатель.




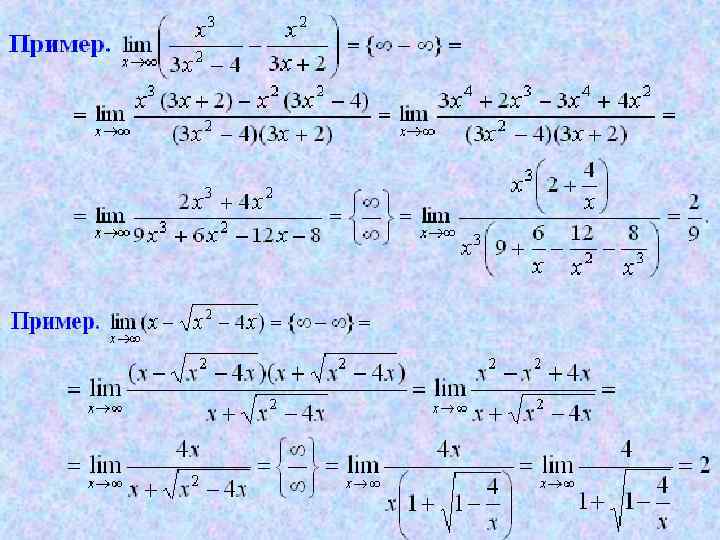

ПЕРВЫЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ

n n Функция не определена при x=0, так как числитель и знаменатель дроби обращаются в нуль. График функции изображен на рисунке. Однако, можно найти предел этой функции при х→ 0.
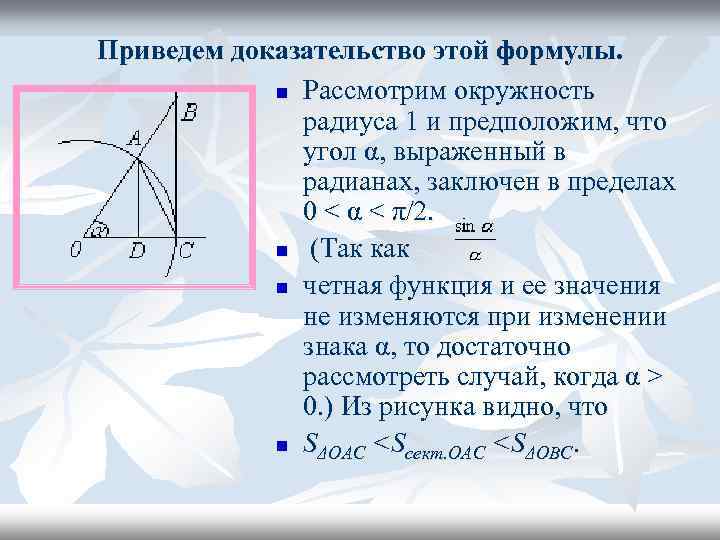
Приведем доказательство этой формулы. n Рассмотрим окружность радиуса 1 и предположим, что угол α, выраженный в радианах, заключен в пределах 0 < α < π/2. n (Так как n четная функция и ее значения не изменяются при изменении знака α, то достаточно рассмотреть случай, когда α > 0. ) Из рисунка видно, что n SΔOAC <Sсект. OAC <SΔOBC.

SΔOAC <Sсект. OAC <SΔOBC. Так как указанные площади соответственно равны n n n SΔOAC=0, 5∙OC∙OA∙sinα=0, 5 sinα, Sсект. OAC=0, 5∙OC 2∙α=0, 5α, SΔOBC=0, 5∙OC∙BC=0, 5 tgα. Следовательно, sin α < tg α. Разделим все члены неравенства на sin α > 0: Поэтому на основании теоремы о двух милиционерах заключаем, что Выведенная формула и называется первым замечательным пределом.

ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
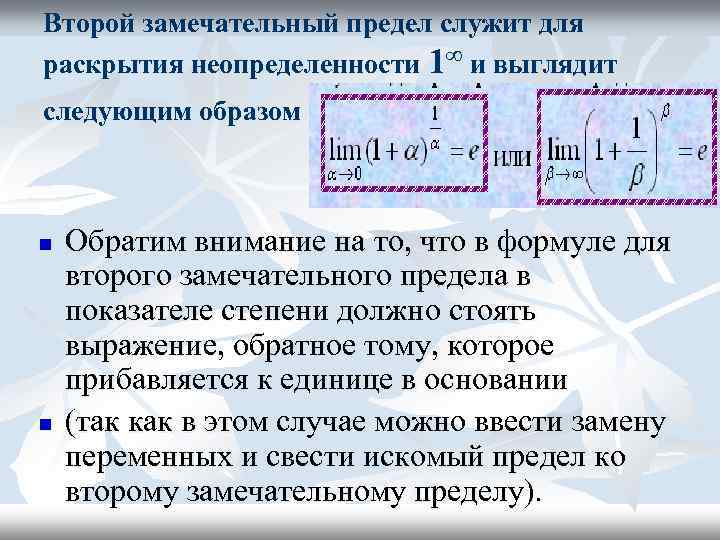
Второй замечательный предел служит для раскрытия неопределенности 1∞ и выглядит следующим образом n n Обратим внимание на то, что в формуле для второго замечательного предела в показателе степени должно стоять выражение, обратное тому, которое прибавляется к единице в основании (так как в этом случае можно ввести замену переменных и свести искомый предел ко второму замечательному пределу).

Примеры.

Сравнение функций.







Эквивалентные бесконечно малые функции приведены в табл. где


Глава 4-4-2.ppt