Бер Л. М. Дифференциальное исчисление ГОУ ВПО НИ

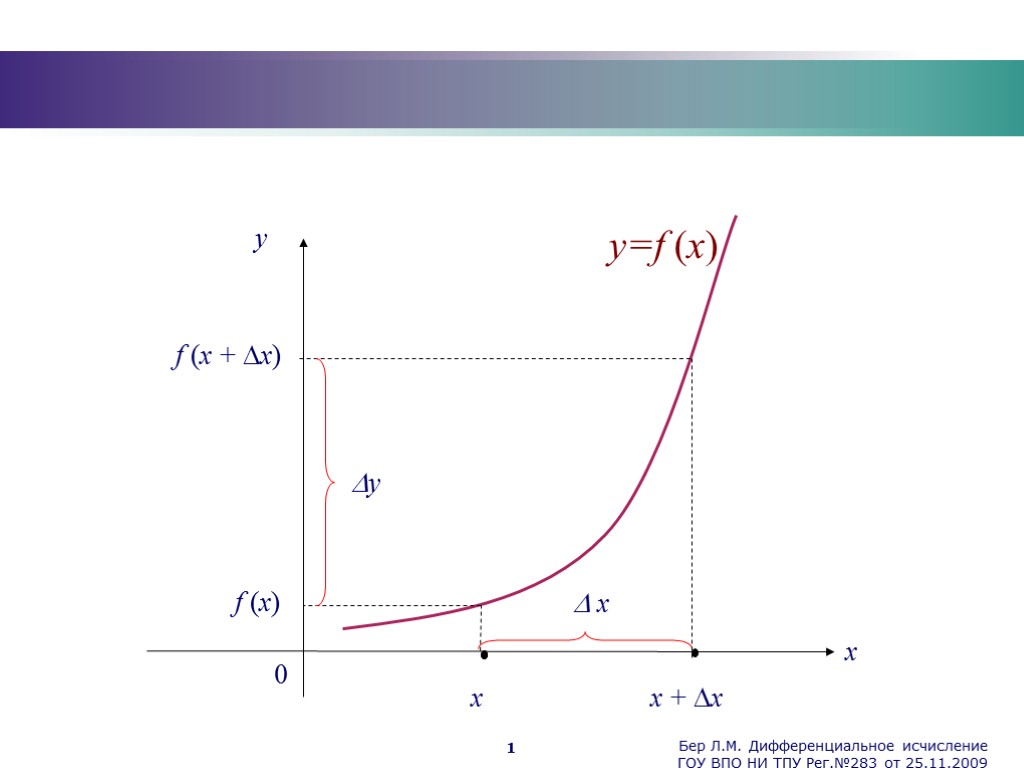
Бер Л.М. Дифференциальное исчисление ГОУ ВПО НИ ТПУ Рег.№283 от 25.11.2009 1 0 y x x f (x) y=f (x) x + x x f (x + x) y

Бер Л.М. Дифференциальное исчисление ГОУ ВПО НИ ТПУ Рег.№283 от 25.11.2009 2 Производная функции Определение. Если существует предел отношения приращения функции f(x) к приращению аргумента x, при стремлении приращения аргумента к нулю, то он называется производной функции в точке x . Обозначения: y, f (x) или , . Определение. Функция, имеющая производную в точке, называется дифференцируемой в этой точке. Функция, называется дифференцируемой в промежутке, если она дифференцируема в каждой точке этого промежутка.

Бер Л.М. Дифференциальное исчисление ГОУ ВПО НИ ТПУ Рег.№283 от 25.11.2009 3 Физический смысл производной Производная характеризует скорость изменения функции в зависимости от изменения аргумента (скорость процесса в любой момент времени). С геометрической точки зрения дифференциру-емость означает, что к графику функции в данной точке можно провести единственную невертикальную касательную.
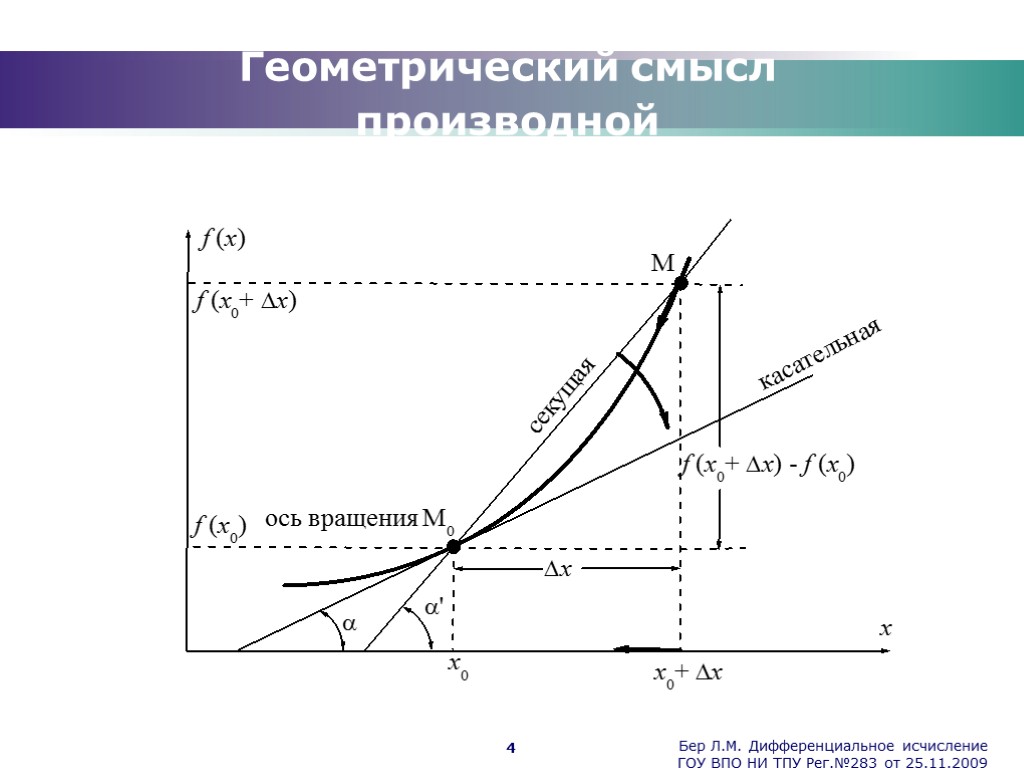
Бер Л.М. Дифференциальное исчисление ГОУ ВПО НИ ТПУ Рег.№283 от 25.11.2009 4 Геометрический смысл производной

Бер Л.М. Дифференциальное исчисление ГОУ ВПО НИ ТПУ Рег.№283 от 25.11.2009 5 Касательная и нормаль Определение. Касательной к графику функции в точке М0(x0, y0 ) назовем предельное положение секущей М0М, когда точка М, двигаясь вдоль кривой, стремиться к совпадению с точкой М0. Уравнение касательной к графику функции в точке М0(x0, y0): . Прямая, проведенная через точку касания, перпендикулярно касательной к графику функции, называется нормалью. Уравнение нормали к графику функции в точке М0(x0, y0):

Бер Л.М. Дифференциальное исчисление ГОУ ВПО НИ ТПУ Рег.№283 от 25.11.2009 6 Правила дифференцирования Теорема 3. Пусть f (x) и g (x) дифференцируемые функции и с константа, тогда справедливы соотношения 1. [c f (x)] = c f (x) . 2. [ f (x) g (x) ] = f (x) g (x) . 3. [ f (x) g (x) ] = f (x) g (x) + f (x) g (x) . 4. .

