Behavioral Game Theory Networked Life CSE 112 Spring

Behavioral Game Theory Networked Life CSE 112 Spring 2004 BGT lectures by Nick Montfort for Prof. Michael Kearns

Another experiment… 6 people to the front, in 3 pairs, for quick economic games…? $$$

The rules 1. A coin flip determines who is player 1. 2. Player 1 chooses to take some number of quarters between 0 and 10. 3. Player 2 gets the rest of the 10 quarters. That’s it. This is a one-shot game. The 3 pairs at the front play 1 game each.

Behavioral Game Theory and Game Practice • Game theory: how rational individuals should behave • Who are these rational individuals? • Behavioral game theory: Look at how people actually behave – experiment by setting up real economic situations – account for people’s economic decisions – don’t break game theory when it works • Fit a model to observations, not “rationality”

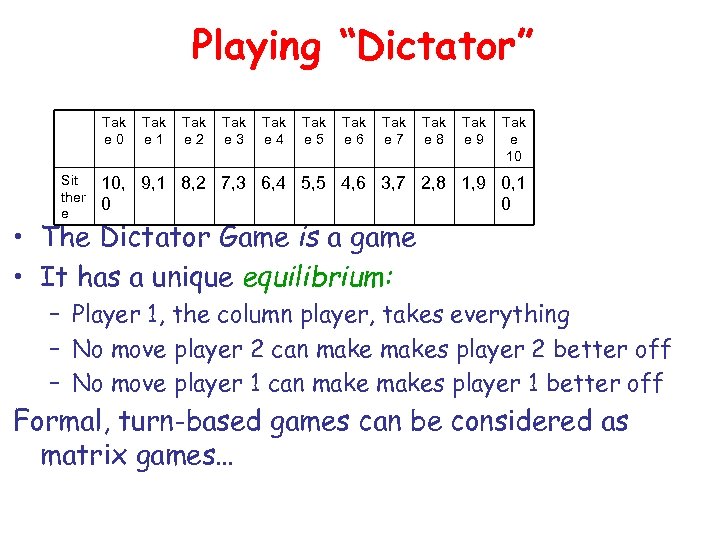
Playing “Dictator” Tak e 0 Sit ther e Tak e 1 Tak e 2 Tak e 3 Tak e 4 Tak e 5 Tak e 6 Tak e 7 Tak e 8 Tak e 9 Tak e 10 10, 9, 1 8, 2 7, 3 6, 4 5, 5 4, 6 3, 7 2, 8 1, 9 0, 1 0 0 • The Dictator Game is a game • It has a unique equilibrium: – Player 1, the column player, takes everything – No move player 2 can makes player 2 better off – No move player 1 can makes player 1 better off Formal, turn-based games can be considered as matrix games…

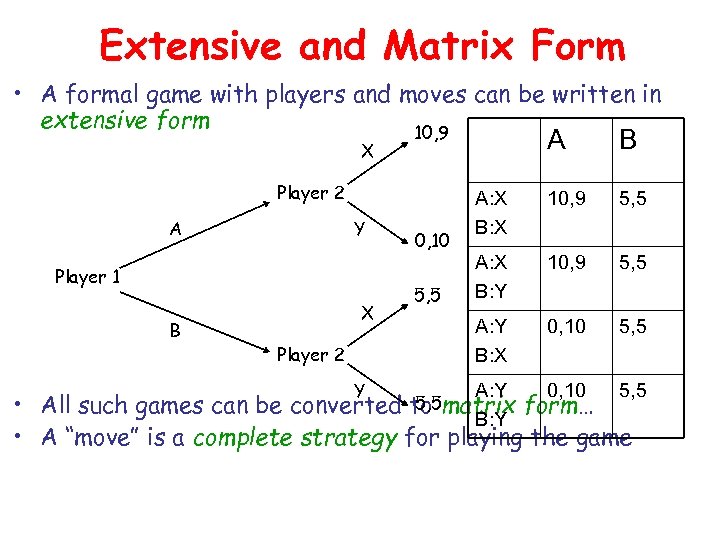
Extensive and Matrix Form • A formal game with players and moves can be written in extensive form 10, 9 A B A: X B: X 10, 9 5, 5 A: X B: Y 10, 9 5, 5 A: Y B: X 0, 10 5, 5 A: Y B: Y 0, 10 5, 5 X Player 2 A Y Player 1 B X Player 2 Y 0, 10 5, 5 • All such games can be converted form… • A “move” is a complete strategy for playing the game 5, 5 to matrix

Ultimatum Bargaining From the first day of class… • Player 1 chooses some division of a surplus (of size 10) • Player 2 can either accept or reject the division • • How many moves for Player 1? How many for Player 2? What does the matrix look like? What equilibrium or equilibria exist?

How People Play Dictator First experiment: Kahneman et al. 1986 Player 1 can only choose ($10, $10) or ($18, $2) 3/4 of dictators chose the equal split People are generous! …or maybe not. Only 10% were paid (? ), choice was limited … Forsyth et al. 1994 Mean allocation of dictators is only about 20%! Frohlich and Oppenheimer 1997 Canadians gave 27%, Americans only 16% Anonymity from experimenters = lower offers from dictators

How People Ultimatum-Bargain Thousands of games have been played in experiments… • • In different cultures around the world With different stakes With different mixes of men and women By students of different majors Pretty much always, two things prove true: 1. 2. Player 1 offers close to, but less than, half (40% or so) Player 2 rejects low offers (20% or less)

Ultimatum Bargaining across Cultures Sharing norms differ in the industrialized world Japan, Israel lowest (Roth et al. 1991) Machiguenga farmers in Peru (Henrich 2000) Offered 26% on average, accepted all but 1 offer Very socially disconnected Ache in Paraguay, Lamelara in Indonesia Made hyperfair (more than 50%) offers Headhunters (potlatch culture), whalers

Ultimatum Bargaining across Majors Economics majors offer 7% less, accept 7% less (Carter and Irons 1991) They must have learned game theory! … but this behavior is consistent across years of study (freshman to seniors) … maybe their game-theoretic nature made them want to study economics? Other studies show no correlation, or that econ/business students offer more.

Ultimatum Bargaining and Looks 70 University of Miami students, photographed and rated for attractiveness (Schweitzer and Solnick 1999) Man as player 1, attractive woman as player 2… Doesn’t make much difference Woman as player 1, attractive man as player 2… Average offer is 50. 7% (hyperfair!) Small percentage (1 or 2? ) offer almost everything

Stakes, Entitlement, Framing Indonesia: from a day’s wages to a month’s wages No difference… Florida: answer questions to get $400 pie instead of $20 More low offers at $400 … but subjects earned it Framing it as a buyer/seller exchange lowers offers 10% Framing it as a resource competition raises them slightly (Hoffman et al. 1994)

Two Problems with Game Theory 1. Doesn’t explain the dictator game 2. Doesn’t explain ultimatum bargaining Can it still help us outsmart people who don’t play game-theoretically? Generally, no. It can only help us beat “rational” opponents — not real people. Does adding something non-strategic like “altruism” fix these problems? It had better fix the dictator game! But it isn’t enough for ultimatum bargaining.

A New Theory… We could create new per-game theories… But this would be useless. We could consider these as repeated games of some sort… But that complicates a lot of things. Maybe we can make a small change to something underlying… What if people don’t only care about their own payoffs?

A New Theory of Utility Consider that people still like their payoffs They also dislike others having more money, with some coefficient . And they dislike having more money than others, with coefficient . U_1 is player 1’s utility; P_1 & P_2 are the players’ payoffs. U_1 = P_1 - (max[P_2 - P_1, 0]) - (max[P_1 - P_2, 0]) is “envy” is “guilt” 0 <= < 1 < Different players can have different and

Inequality Aversion U_1 = P_1 - _1(max[P_2 - P_1, 0]) - _1(max[P_1 - P_2, 0]) (Fehr and Schmidt 1999) Now, we can do classical game theory, but with U, not P Player 2 should reject any offer < _2/(1 + 2 _2) If = 1/3, player 2 should reject any offer less than 20% Player 1 offers will depend on Estimates of player 2 envy ( _2) distribution and Player 1 guilt ( _1)

Inequality Aversion: Advantages • • Model generalizes easily to more than 2 players = 1/3, = 0 can explain a lot! • Ultimatum bargaining • Multi-player ultimatum bargaining (“Market game”) • Even dictator games Parameters can be tuned for cultures or individuals Does not break most of the existing, correct predictions of non-IA game theory

Inequality Aversion: A Problem… Consider the following game: Player 1 can give 5% or 90% (no other options) Player 2 can accept or reject Will Player 2 reject an offer of 5%? What if Player 1 could give only 10% or 95%? Still, we’re making progress.

Inequality Aversion on Graphs Finally! We’re getting back to networks. . . For games where IA game theory works, we could put these games on graphs. Do players care about global inequalities or neighborhood inequalities? Our guesses may agree, but it’s an open question: no experiment has been done!

Next time… • Experiment • Discussion of different (more interesting? ) multi-player games… • …and learning in games… • …and attempts at randomness.

Another experiment… 5 people to the front for quick economic games…? $$$

The rules 1. All 5 people move at once by writing down a number between 0 and 100. 2. The one with the number that is closest to 2/3 of the average is the winner, getting $1. 3. If several people all are closest, Kilian will pick a winner randomly using random. org. That’s it. We will repeat this game.

First, to return to Ultimatum Bargaining… To clarify: • • Player 1 offers 4 Player 2 accepts 4 or greater but rejects 3 or less This is a Nash equilibrium. So is any set of actions where player 1 offers N and player 2 accepts N (no matter what player 2 does in the other cases. ) But it isn’t a subgame perfect equilibrium.

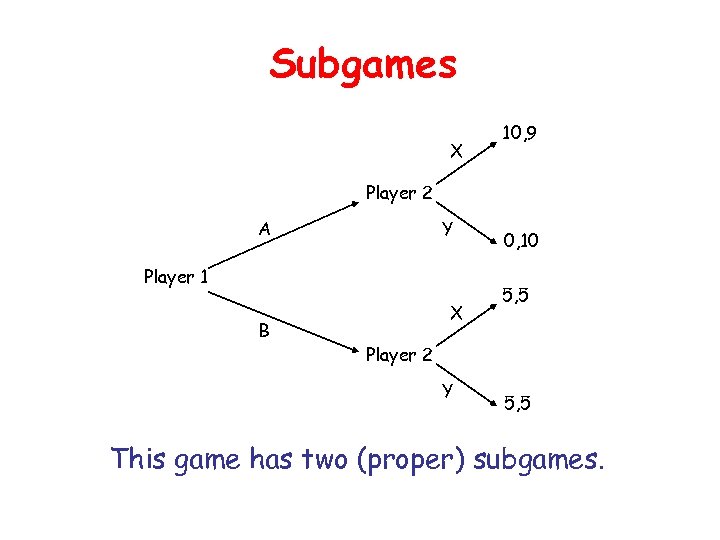
Subgames X 10, 9 Player 2 A Y Player 1 B X 0, 10 5, 5 Player 2 Y 5, 5 This game has two (proper) subgames.

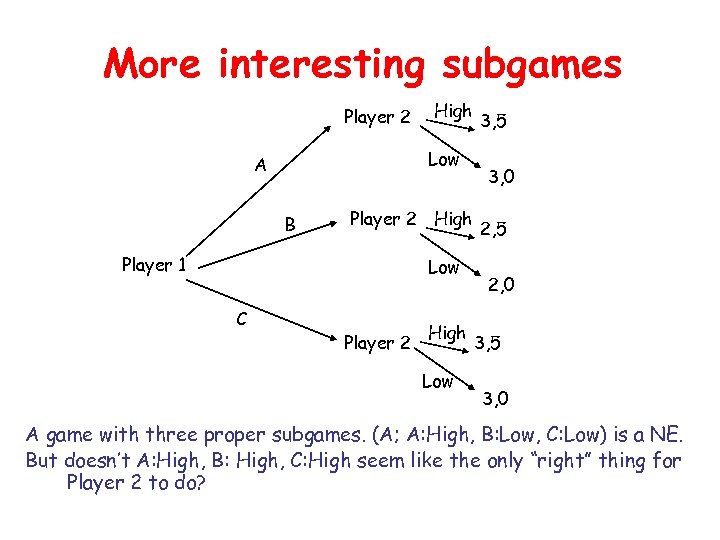
More interesting subgames Player 2 High Low A B Player 2 High Player 1 Low C Player 2 High Low 3, 5 3, 0 2, 5 2, 0 3, 5 3, 0 A game with three proper subgames. (A; A: High, B: Low, C: Low) is a NE. But doesn’t A: High, B: High, C: High seem like the only “right” thing for Player 2 to do?

Subgame perfect equilibria How many proper subgames are there in Ultimatum Bargaining (10 unit surplus)? What is the dominant strategy for player 2 in each one? Which other games is this sensible for: • Prisoner’s dilemma? • Rock, paper, scissors? • Dictator? • The game we played at the beginning of class? Only turn-based games that actually have proper subgames.

Beauty Contest Some number of players try to guess a number that is 2/3 of the average guess. The answer can’t be between 68 and 100 - no use guessing in that interval. It is dominated. But if no one guesses in that interval, the answer won’t be greater than 44. But if no one guesses more than 44, the answer won’t be greater than 29… Everyone should guess 0! And good game theorists would… But they’d lose…

Iterated Dominance People don’t instantly compute all the way to 0 The median subject uses 1 or 2 rounds of iteration (25, 35) Guessing 0 on the first round (game theorist) is poor Guessing 30 (behavioral game theory) is much better But 30 isn’t a good guess the seventh time you play…

A Digression: Randomness Another experiment. No money this time, but this is going to help you win at RPS! Everyone, count off into two groups… Half the class (group 1): Flip a coin 20 times and record the results. The other half (group 2): Write down a sequence that you think looks like 20 random coin flips. Write the sequence on paper; write “ 1” or “ 2” on the back.

Subjective Randomization People randomize better when they’re paid to be random World RPS championship: probably a good entropy pool! Binary random choices (simulating coin flips): • Often come up exactly 50/50 • Have too few runs of identical choices: (n+1)/2 expected • Have longest runs that are too short (5 or 6 per 20) Alternating (“negative recency”) is a common artifact Oddly, children seem to learn this around grade 5!

Back to Multiplayer Games: Centipede A four-turn game with 5 possible payoffs: 1. 2. 3. 4. P 1 can take (0. 4, 0. 1) or pass P 2 can take (0. 2, 0. 8) or pass P 1 can take (1. 6, 0. 4) or pass P 2 can take (. 8, 3. 2) or pass (6. 4, 1. 6) What should happen? What does happen? Cond. prob of take: 0. 06 0. 32 0. 57 0. 75 in trials 1 -5 0. 08 0. 49 0. 75 0. 82 in trials 6 -10

Continental Divide A group of 7 plays the game 15 times Players pick numbers between 1 -14; they win by coordinating — choosing close to the median Two “peaks” of payoff provide equilibira points, at 3 (payoff 60) and 12 (payoff 112) Between 7 and 8 is the “divide” A few people who have 7 as a lucky number can drive the group to the low-payoff equilibrium Or, a few choosing 8 can lead to the better one

Learning How do people learn as they play economic games? • • • Evolution: They don’t! (But can die off or prevail) Reinforcement: Choices that pay off well (and maybe similar ones) are made more likely Belief learning: Build a model of the opponent • • • Fictitious play Cournot best-response dynamics Imitation: Do what the most successful player is doing Rule Learning: Reinforce general rules, not actions Experience-Weighted Attraction: Integrates RL & Belief (And there are others…)

Evolutionary approaches are actually the opposite of learning Individuals have fixed strategies they are born with The population as a whole evolves, but individuals do not learn — they either die or survive Some machine learning researchers have considered merging evolutionary approaches and learning: let some individuals have the capability for learning (Cervone et al. 2000)

Reinforcement Learning In the simplest form: • Make actions that result in high payoffs more likely We could smooth the probabilities to neighboring actions (if we know what “neighboring” means) One problem with a pure RL approach: People learn actions that are never reinforced

Belief Learning Two extremes: • Fictitious play Build a model of what the other player does based on past history (25% action A, 50% action B…) • • • Cumulate (1 st action is as important as most recent) Weight more recent actions more heavily/discount the past Cournot best-response dynamics Assume your opponent will repeat the last action, and pick the best respose to that

Imitation May explain a lot of business activity… What looks like imitation may be a simplified form of other learning, or one heuristic of many Can’t explain innovation (or how the best player plays)

Rule Learning Instead of learning strategies directly, learn decision rules that allow you to choose strategies Decisions are made using a mixture of experts One way to model how different ways of learning are combined…

Experience Weighted Attraction Another way to integrate learning approaches: (Camerer and Ho, 1999) • • One parameter mixes between belief and reinforcement learning One adjusts between cumulative beliefs and weighted beliefs (Two other parameters…) A functional version sets these four parameters from past history and a single parameter. A good fit, and suggests how to integrate different types of learning.