Растровые алгоритмы.ppt
- Количество слайдов: 17

Базовые растровые алгоритмы

Характеристики растра: Разрешающая способность растра – расстояние между соседними точками растрового изображения и измеряется в dpi = 25. 4 / d. P Связность – соседство двух пикселей в растровом изображении.
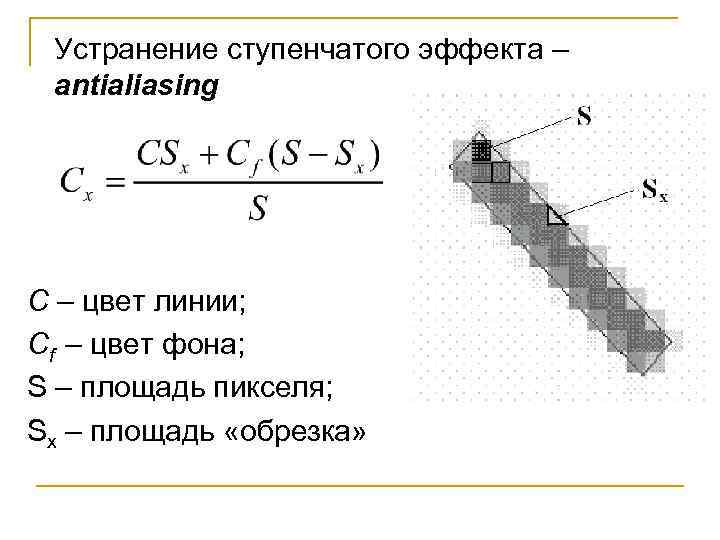
Устранение ступенчатого эффекта – antialiasing C – цвет линии; Cf – цвет фона; S – площадь пикселя; Sx – площадь «обрезка»
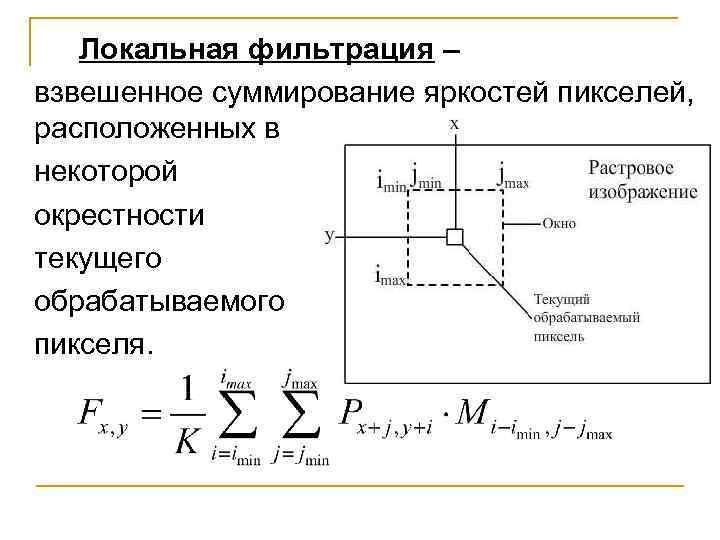
Локальная фильтрация – взвешенное суммирование яркостей пикселей, расположенных в некоторой окрестности текущего обрабатываемого пикселя.

Эмуляция оттенков – дизеринг (dithering) увеличение количества оттенков цветов за счет снижения пространственного разрешения растрового изображения (обмен разрешающей способности на количество цветов) где S 1 и S 2 – части площади, занятые пикселями цветов C 1 и C 2 соответственно

Если ячейку представить в виде плотно прижатых квадратных пикселей, то от площадей легко перейдём к количеству пикселей соответствующего цвета в ячейке:
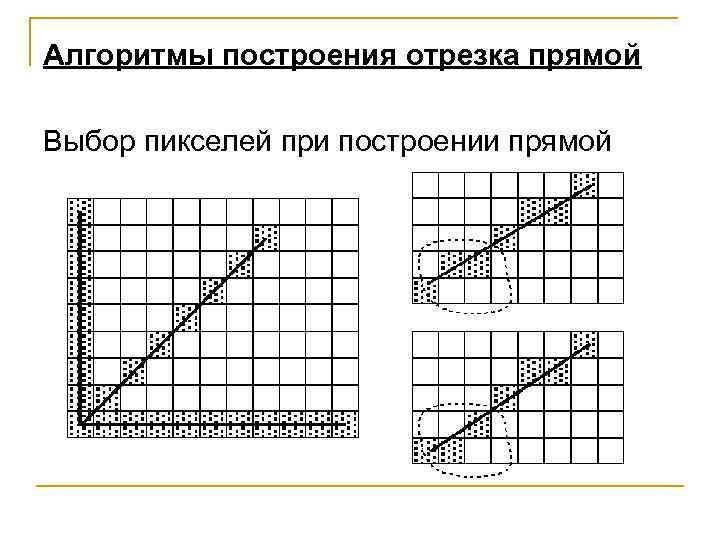
Алгоритмы построения отрезка прямой Выбор пикселей при построении прямой

Параметрический способ рисования: Преимущества: самый простой алгоритм Недостатки: работа с дробными числами
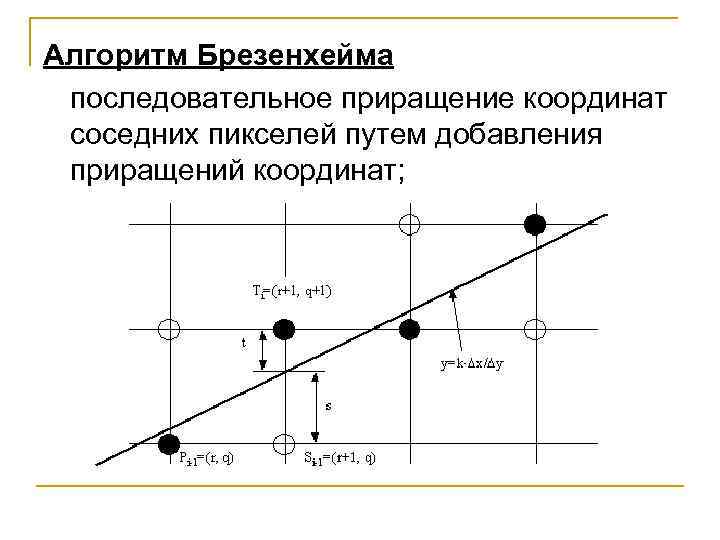
Алгоритм Брезенхейма последовательное приращение координат соседних пикселей путем добавления приращений координат;
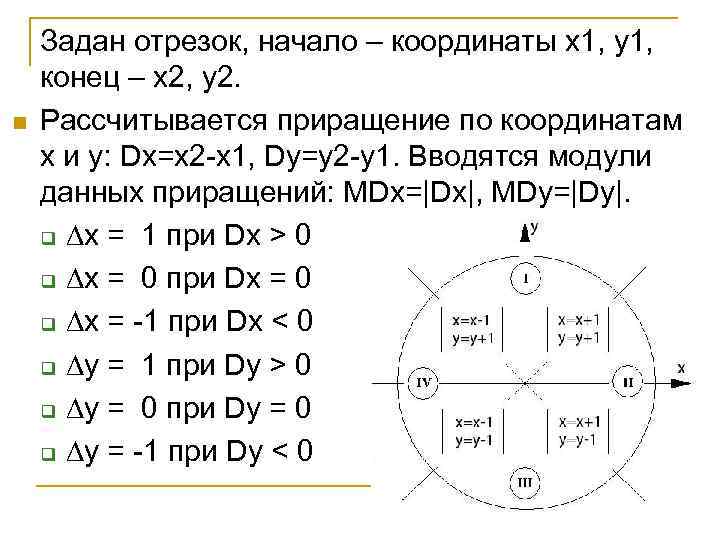
n Задан отрезок, начало – координаты x 1, y 1, конец – x 2, y 2. Рассчитывается приращение по координатам x и y: Dx=x 2 -x 1, Dy=y 2 -y 1. Вводятся модули данных приращений: MDx=|Dx|, MDy=|Dy|. q ∆x = 1 при Dx > 0 q ∆x = 0 при Dx = 0 q ∆x = -1 при Dx < 0 q ∆y = 1 при Dy > 0 q ∆y = 0 при Dy = 0 q ∆y = -1 при Dy < 0

Перед началом итерационного цикла введем начальные присваивания: x=x 1, y=y 1, δx = MDx, δy = MDx, D = max (MDx, MDy) Итерационный цикл: Повторять D+1 раз: { δx = δx + MDx δy = δy + MDy Если δx >= D, тогда δx = δx – D, x = x+ ∆x Если δy >= D, тогда δy = δy – D, y = y+ ∆y }
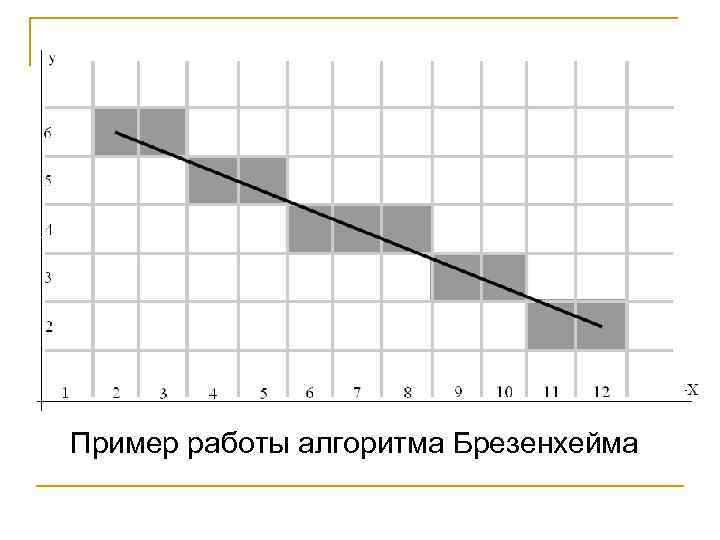
Пример работы алгоритма Брезенхейма

Алгоритм рисования окружности Уравнение окружности: (x-x 0)2 + (y-y 0)2 = R 2 Рисуем только одну восьмую часть окружности — от π/2 до π/4, по часовой стрелке. Z = f (x, y)=(x-x 0)2 + (y-y 0)2 - R 2 Z = 0 – точки на кривой; Z > 0 – точки выше кривой; Z < 0 – точки ниже кривой; Допустимые шаги - вправо и вправо по диагонали Поэтому анализируем Z > 0 (т. е. выход выше f(x))


Недостатки многих инкрементных алгоритмов: n n n Вырожденные эллипсы (a=0 или b=0) рисуются неправильно. Эллипсы с очень большим радиусом могут приводить к переполнению целочисленных переменных, используемых в алгоритме. Пиксели с координатами (±a, 0) и (0, ±b) будут сформированы дважды, что является крупным неудобством

Простое рекурсивное закрашивание x, y – текущий анализируемый пиксель; Color – цвет пикселя, Bcolor – цвет фона C: =Get. Pixel (x, y) If (C<>BColor) and (C<>Color) then Begin Put. Pixel (x, y, Color); Pixel. Fill (x+1, y, BColor, Color); Pixel. Fill (x, y+1, BColor, Color); Pixel. Fill (x-1, y, BColor, Color); Pixel. Fill (x, y-1, BColor, Color); End;

Алгоритм закрашивания линиями Имеется затравочная точка с координатами (xst, yst) n Находятся x. L и x. R – левая и правая границы, между которыми проводится текущая горизонтальная линия. n Делается приращение у=у+dir и, между x. L и x. R, анализируется цвет пикселей над линией. n Делается приращение y=y–dir и, между x. L и x. R анализируется цвет пикселей под линией. n
Растровые алгоритмы.ppt