Базовые понятия синергетики.ppt
- Количество слайдов: 65
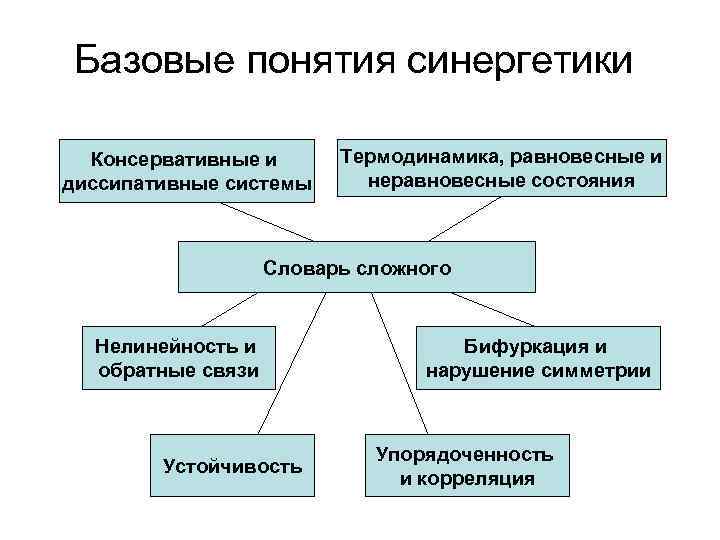
Базовые понятия синергетики Консервативные и диссипативные системы Термодинамика, равновесные и неравновесные состояния Словарь сложного Нелинейность и обратные связи Устойчивость Бифуркация и нарушение симметрии Упорядоченность и корреляция

Консервативные системы • Мир рассматривается как консервативная система, в которой несмотря на разнообразные обменные процессы между разными частями, существует некий первичный элемент, не подверженный изменениям. У греческих мыслителей ключевую роль играет понятие сохранения. В период Ньютона-Лейбница с появлением классической механики идея консервативности существенно укрепляется. Была некоторая непроверенная аксиома, отражающая сохранение. Теперь эта гипотеза -следствие ряда законов, дающих консервативное объяснение движению небесных тел и движению различных предметов под действием земного притяжения. Из второго и третьего законов механики Ньютона, связывающих соответственно силы с ускорением и действие с противодействием, следует, что в системе взаимодействующих точечных масс (в отсутствии внешнего влияния) остаются постоянными следующие три величины: полная энергия (Е), полное количество движения (Р), полный момент движения (L). Центральные силы взаимодействия между частицами, движущиеся в точках ri и rj со скоростями vi и vj. Согласно третьему закону Ньютона Fij=-Fji.

1. Полная энергия: Е = кинетическая энергия+потенциальная энергия = Где mi и vi – масса и скорость i–й материальной точки соответственно; vij потенциальная энергия взаимодействия i–ой и j–й точек, связанная и действующая между ними силой Fij соотношением. Работа силы = изменение потенциальной энергии. Если сила зависит лишь от расстояния между материальными точками r = ri + rj, то это соотношение принимает вид где символ обозначает производную от потенциальной энергии по расстоянию. 2. Полное количество движения.

3. Полный момент количества движения. Где li - момент количества движения i–й материальной точки относительно начала координат. Ключевое свойство основных уравнений механики состоит в том, что величиной динамически связанной с силой является вторая производная координат: т. е. преобразование t’ = -t ничего качественно не меняет и движение идет по тем же траекториям, но в обратном направлении. Т. о. , в уравнениях движения нет ничего такого, что позволило бы различить прямое и обращенное движение.

Классическая механика - наука о системах, являющихся одновременно консервативными и обратимыми во времени. Это наглядно демонстрирует гамильтонов формализм, в котором структура уравнений движения связана с энергией – самой важной из трех сохраняющихся величин. Н – гамильтониан Н = Н(рq) = Е = const p = mv - обобщенный импульс; q = r - обобщенная координата. Для консервативных систем гамильтониан представляет полную энергию (выраженную как функция координат и импульсов), т. е. в классическом смысле — сумму кинетической и потенциальной энергий системы Уравнение и соотношение v = dr/dt эквивалентны следующим выражениям Термины сопровождающие консервативные системы: фазовое пространство, равновесие. . . Аналогом консервативных систем механики являются распространение света в вакууме, описываемое уравнениями Максвелла.

Пространство, каждая точка которого соответствует состоянию динамической системы, называется ее фазовым пространством. Координаты Ф. П. обычные пространственные координаты и импульсы уравнения Гамильтона. Траекторию можно рассматривать как линии тока гипотетической фазовой жидкости. Если v - векторное поле скоростей динамической системы, то фазовая жидкость при называется несжимаемой, а при сжимаемой. В случае любой гамильтоновой системы фазовая жидкость несжимаемая. Теорема Лиувилля доказывает, что фазовая жидкость любой гамильтоновой системы несжимаема. Объем фазовой жидкости со временем не меняется, изменяется только формы.

Диссипативные системы. • • Начиная с работ Фурье и Клаузиуса в XIX веке, вырос интерес к диссипативным системам, приводящим к необратимым процессам. Диссипативные системы – широкий класс естественных систем. Ярче всего различия между консервативными и диссипативными системами проявляются при попытке макроскопического описания последних, когда для определения мгновенного состояния системы используются такие коллективные переменные как температура, концентрация, давление, конвективная скорость и др. Примеры диссипативных систем – теплопроводность, диффузия, отражение, нарушение симметрии t’= -t. Рассмотрим систему Лоренца. Имеем т. е. объем фазовой жидкости –отрицателен, фазовая жидкость сжимаема и система диссипативна.

Термодинамика, равновесные и неравновесные состояния Термодинамика-раздел физики, изучающий свойства макроскопических систем в состоянии термодинамического равновесия и процессы перехода между этими состояниями. Энтропия (греч. entropia – поворот, превращение) Энтропия в термодинамике – мера необратимого рассеяния энергии. Энтропия в статистической физике – мера вероятности осуществления какого-либо макроскопического состояния. Энтропия в теории информации – мера неопределенности.

Начала термодинамики и самоорганизация По Клазиусу: Энтропия в замкнутой системе непрестанно возрастает до тех пор, пока не достигает своего максимального значения в состоянии термодинамического равновесия. По Больцману и Планку, между энтропией S и термодинамической вероятностью W существует соотношение (1) S = k. B ln W (k. B – постоянная Больцмана), увеличение энтропии соответствует переходу в более вероятные состояния, и последние более неупорядочены. Постоянная Больцмана – одна из фундаментальных физических констант, равна отношению газовой постоянной R к числу Авогадро Na. Постоянная Больцмана связывает в уравнении состояния идеального газа энтропию физического состояния системы с ее термодинамической вероятностью. k. B = 1. 3806… x 10 23 дж/К.

Людвиг Больцман — один из создателей молекулянокинетической теории газов • Людвиг Больцман показал взаимосвязь между движением атомов и молекул с одной стороны и макроскопическими свойствами материи, такими как температура и давление, с другой. В рамках такой картины давление газа обусловлено упругими ударами молекул газа о стенки сосуда, а температура — скоростью движения молекул (а точнее, их кинетической энергией). Т. е. чем быстрее движутся молекулы, тем выше температура. • Постоянная Больцмана дает возможность напрямую связать характеристики микромира с характеристиками макромира — в частности, с показаниями термометра. Ключевая формула, устанавливающая это соотношение: 1/2 mv 2 = k. T Здесь: m и v — соответственно масса и средняя скорость движения молекул газа, Т — температура газа (по абсолютной шкале Кельвина), а k — постоянная Больцмана. Это уравнение прокладывает мостик между двумя мирами, связывая характеристики атомного уровня (в левой части) с объемными свойствами (в правой части), которые можно измерить при помощи приборов, в данном случае термометров. Эту связь обеспечивает постоянная Больцмана k, равная 1, 38 x 10– 23 Дж/К.

Постоянная Больцмана • Раздел физики, изучающий связи между явлениями микромира и макромира, называется статистическая механика. Одно из основных соотношений статистической механике называется уравнением Больцмана: S = k log p + b • где S — энтропия системы (см. второе начало термодинамики), p — так называемый статистический вес (очень важный элемент статистического подхода), а b — еще одна константа. Всю жизнь Л. Больцман в буквальном смысле опережал свое время, разрабатывая основы современной атомной теории строения материи, вступая в яростные споры с подавляющим консервативным большинством современного ему научного сообщества, считавшего атомы лишь условностью, удобной для расчетов, но не объектами реального мира. Когда его статистический подход не встретил ни малейшего понимания даже после появления специальной теории относительности, Больцман в минуту глубокой депрессии покончил с собой. Уравнение Больцмана высечено на его надгробном памятнике.

Идеальный газ – теоретическая модель газа, в которой не учитывается взаимодействие частиц газа, а свойства описываются законами классической физики ( уравнением Клайперона – Менделеева). Частицы классического идеального газа распределены по энергиям согласно распределению Больцмана. Моделью идеального газа хорошо описываются только те реальные газы, которые достаточно разрежены. Число Авогадро Na число структурных элементов ( атомов, молекул, ионов и др. ) в единице количества вещества (в одном моле) Na = 6. 02 х 1023 моль 1 . Ещё в XIX веке основатели термодинамики пришли к заключению, что порядок может возникнуть только при условии, если к системе подводится высокоценная энергия, а от системы отводится малоценная энергия. Майер и Больцман особенно подчёркивали роль Солнца как движущей силы структурообразования на нашей планете.

Основные законы термодинамики: три начала термодинамики; фундаментальное уравнение Гиббса Рассмотрим макроскопическую систему, характеризуемую: • экстенсивными параметрами (энергия E, энтропия S, объём V, количество химических компонент N 1, N 2, …, Ns); это параметры, значения которых пропорциональны массе термодинамической системы или ее объему (т. е. значения э. п. системы равно сумме его значений для отд. частей системы); • интенсивными параметрами (температура T, давление p, концентрация и др. ); это параметры не зависящие от массы системы, т. е. имеют одинаковые значения для любой макроскопической части однородной термодинамической сист, находящейся в состоянии равновесия. В качестве единицы количества вещества используем в зависимости от целесообразности 1 частицу или 6, 023· 1023 частиц. В общих формулах выбор единицы не играет никакой роли.

Первое начало термодинамики утверждает, что если система совершает термодинамический цикл, то полное количество теплоты сообщаемое системе равно сумме приращений внутренней энергии и совершенной системой элементарной работы, т. е. имеет место интерпретация закона сохранения энергии. Энергия не рождается и не исчезает. Энергия – количественная величина, баланс которой может быть записан как: d. E = de. E + di. E (1) Изменение количества энергии в системе равно сумме двух вкладов, учитывающих, соответственно, обмен энергией (de. E) и производство энергии (di. E). Поскольку энергия не может ни рождаться, ни исчезать, di. E = 0 Слагаемое, описывающее обмен энергией, можно представить в виде суммы совершаемой работы (d´A) и подведённого тепла (d´Q) : de. E = d´A + d´Q. (2)

В случае квазистатического процесса обменный член можно представить в виде билинейной формы: (3) de. E = Здесь li и Li – сопряжённые переменные работы, например, l 1 = p и L 1 = V ; µk – химический потенциал k й компоненты; de изменение числа частиц, вызванное обменом; Nk часть потока энергии, не связанная с изменением координат работы или с обменом частицами. В реальных (необратимых) процессах необходимо учитывать ещё один вклад d´Aнеобр: (4) de. E = Здесь d´Aнеобр – часть работы, связанная с необратимыми процессами, происходящими внутри системы, например, с трением.

Второе начало термодинамики утверждает, что существует функция состояния системы S, приращение которой ds при обратимом сообщении системе теплоты равно При реальных (необратимых) адиабатических процессах di. S 0, Т. е. энтропия возрастает, достигая максимального значения в состоянии равновесия. Энтропия может только рождаться, но не уничтожаться. Энтропия – также количественная величина, баланс которой можно представить в виде: (5) d. S = de. S + di. S. Так как энтропия не может уничтожаться, справедливо неравенство (6) di. S 0. Обменный член, по Клазиусу, прямо пропорционален подведённому теплу и обратно пропорционален температуре: (7) По Больцману и Планку, энтропия системы служит мерой царящего в ней беспорядка. По Освальду, энтропию можно рассматривать и как количественную меру величины содержащейся в системе энергии.

Третье начало термодинамики. Теорема Нернста: Энтропия любой системы при абсолютном нуле температуры всегда может быть принята равной нулю Энтропия и энергия – ограничены снизу переменными состояния, и при (8) подходящем выборе начала отсчёта можно считать, что: S 0 и E = 0. По Нернсту и Планку, энтропия системы, находящейся в равновесии относительно внутренних переменных, обращается в нуль при абсолютном нуле температуры вместе со своими производными по экстенсивным (9) переменным; S = 0 и при T = 0. Энтропия тела при конечной температуре всегда больше, чем при T = 0, откуда и следует, что S > 0 при T > 0. Положительность энтропии гарантируется, если учесть энергию покоя E 0 = m 0 c 2 по Эйнштейну (m 0 – масса покоя).

Уравнение Гиббса. Устанавливает взаимосвязь между экстенсивными переменными состояния E, S и L. Обоснование соотношения следует из первых двух начал термодинамики. Из соотношений (2) (4) и (7) для квазистатического процесса следует, что (10) Это означает, что при квазистатическом переходе из состояния 1 в соседнее состояние 2 изменения энергии, энтропии и координат Li связаны между собой линейным соотношением. Так как в соотношение (10) входят только переменные состояния, оно должно выполняться и для необратимых переходов из состояния 1 в состояние 2, поскольку значения переменных состояния не зависят от пути, по которому происходит переход. Тем самым, предполагается, что фундаментальное уравнение Гиббса должно распространяться и на необратимые переходы при условии, что значения переменных состояния в начальном и конечном состояниях вполне определены.

Частные случаи а) изолированная система (макроскопически). Для такой системы справедливо: (11) de. E = 0, d. S = di. S 0. Энтропия – монотонная неубывающая функция времени, асимптотически стремящаяся при больших временах к максимальному значения, соответствующему равновесным значениям термодинамических параметров (энергии, объёма и т. д. ). Следовательно, макроскопически изолированная система со временем приближается к состоянию с максимальным неупорядочением.

б) замкнутая система. По определению, такая система не может обмениваться веществом (на макроскопическим уровне) с окружающей средой. Отсюда: (12) d. E = de. E = , , , (13) Последнее неравенство (неравенство Клазиуса-Карно) означает, что подвод тепла увеличивает беспорядок, в то время как увеличение порядка (уменьшение энтропии) требует отвода тепла d Q < 0.

Образование структур при отводе тепла (переходе к более низким температурам) – универсальное свойство материи. Известно, что физические тела при низких температурах переходят в агрегатное состояние с большей степенью упорядоченности, например, в кристаллическое состояние. При низких температурах становятся реализуемыми относительно маловероятные состояния с малыми энергиями, соответствующие более высокой степени упорядочения. Это следует из распределения вероятностей Больцмана (14) , делающее при низких температурах более предпочтительными состояния с малыми энергиями Ei. Другая возможность отвести энергию из замкнутой системы состоит в том, чтобы подводить к системе тепло при более высокой температуре и отводить тепло при более низкой температуре (это механизм экспорта энтропии нашей Землёй). Величина d Q в соотношении (12) означает бесконечно малое количество тепла, подведённое к системе из окружающей среды; li – координаты работы экстенсивного характера, li – коэффициенты работы интенсивного характера. Наряду с обратимой работой система может также совершать и необратимую работу, например, при вязкости и проводимости. Например, при прохождении электрического тока силы I, индуцированного приложенным извне напряжением Ф, справедливо: d Aнеобр = IФdt. (15)

в) открытые системы. Определение работы задаётся соотношение (4). Хотя вычисление работы по действующим извне причинам, например, работы электрических сил, работы трения, работы расширения, работы ускорения может оказаться сложным, однако эта работа всегда вполне определена. Нетривиально и неоднозначно разделение между бесконечно малой работой и бесконечно малым количество тепла. Пусть система имеет температуру T, химические потенциалы k и парциальные мольные энтропии sk , k = 1, 2, …, s. Пусть изменение количества k-ой компоненты состоит из вклада внутренних реакций и вклада обмена веществ: d. Nk = di. Nk + de. Nk. (16) Подставляя в фундаментальное уравнение Гиббса: (17) Если в правой и левой частях уравнения сохранить только вклады внутренних (диссипативных) процессов, то с учётом соотношения (12): (18)

В химической литературе отдаётся предпочтение другому определению потока тепла: (19) В этом случае: (20) Ещё одна возможность определения теплового потока: В этом случае: (21) (22) где парциальные мольные энтропии определяются соотношением hk = k + Tsk.

Поток тепла d*Q, как правило, называется приведённым теплом. Это определение потока тепла в открытых системах обладает рядом принципиальных преимуществ. 1. Представление приведённого потока тепла d*Q по формуле (22) показывает в явном виде, что обмен веществом сопряжён с обменом энтропией. 2. Если к однородной жидкой смеси добавить жидкость с теми же параметрами, то d*Q =0. Ни одно другое определение потока тепла не позволяет достичь этого свойства. 3. Приведённый поток тепла d*Q инвариантен относительно сдвига нулевой точки внутренней энергии и относительно изменения относительной скорости. 4. Выражение для производства энтропии принимает при использовании приведённого теплового потока особенно симметричную форму. В открытых системах изменение энтропии d. S не имеет определённого знака. В зависимости от теплообмена и обмена веществом изменение энтропии может быть и положительным, и отрицательным.

Глобальные условия самоорганизации Энтропия является ключевой физической величиной при описании самоорганизации. Она служит мерой ценности содержащейся в системе энергии и мерой беспорядка. Самоорганизация связана с ценными формами энергии и с упорядоченными состояниями системы. Энтропия системы может уменьшаться, если система экспортирует энтропию (de. S<0) и если экспорт в единицу времени превосходит соответствующее производство энтропии внутри системы, т. е. d. S < 0, если |de. S| > di. S 0. (23) Такая ситуация мыслима только вдали от равновесия, поскольку вблизи равновесия всегда доминирует неравенство di. S > 0. Для того чтобы в системе могло начаться образование структур, экспорт энтропии должен превзойти некоторое критическое значение. Самоорганизация – явление «надкритическое» , или «закритическое» . Это означает, что оно возможно, если параметр системы превосходит определённое критическое значение.

Экспорт энтропии, превосходящий производство энтропии, возникает не спонтанно, а требует «энтропийного насоса» . Для приведения этого насоса в действие, как для приведения в действие любой машины, необходима расходуемая свободная энергия или свободная энтальпия, которую насос может черпать из внешних или внутренних источников. В конечном счёте, такие источники энергии всегда могут быть сведены к ядерным или химическим реакциям, протекающих на Земле или на звёздах. Энтропийные насосы встречаются как внутри, так и вне структурообразующей системы. Соответственно, различают активные и пассивные структурообразующие системы. Пассивные структурообразующие системы (ячейки Бенара, электрические цепи, лазеры и т. д. ) непременно должны быть связаны с окружающей средой. Окружающая среда должна содержать энтропийные насосы, которые накачивают в систему электричество, тепло при более высокой температуре или коротковолновое излучение. Активные структурообразующие системы (живые организмы и др. ) содержат энтропийные насосы внутри себя и поэтому должны, как правило, обладать высокой внутренней организацией. Кроме того, активные структурообразовательные системы должны получать из окружающей среды приток высокоэнергитичных сырьевых веществ. Таким образом, энтропийный насос уводит как активные, так и пассивные системы в сторону от равновесия.

Если система сильно отклоняется от равновесия, то переменные, вообще говоря, удовлетворяют уже не линейным уравнениям, а более глубоким нелинейным закономерностям. Нелинейность – существенная и общая характерная особенность сильно неравновесных процессов, протекающих в природе. С другой стороны, надкритический экспорт энтропии требует особых внутренних структур системы. Самоорганизация является свойством материи, существующем лишь при специфических внутренних и внешних условиях. Самоорганизация не ограничена каким либо особым классом веществ. Краткое заключение: в природе существуют необратимые процессы двух основных типов: искажение или возмущение структур в окрестности равновесия как общее свойство систем при произвольных условиях; образование структур вдали от равновесия при специальных внутренних и внешних условиях; к числу этих условий принадлежат нелинейность внутренней динамики и надкритичность значения внешних параметров системы.

Пригожин предложил называть устойчивые пространственные, временные или пространственно временные структуры, образующиеся вдали от равновесия при надкритических значениях параметров в нелинейной области, диссипативными структурами. Каждый из отличительных признаков, отобранных и включенных в определение диссипативной структуры, имеет определённое значение для процесса. К числу наиболее важных признаков относятся устойчивость относительно малых возмущений и надкритическое расстояние от равновесия. Важнейший подкласс диссипативных структур образуют стационарные диссипативные структуры, которые при постоянных внешних условиях не претерпевают изменений со временем.

Механическое и термодинамическое равновесия. Неравновесные ограничения В механике равновесие представляет собой особое состояние, в котором как скорости, так и ускорения всех материальных точек равны нулю. По определению результирующая сила, действующая на каждую точку в любой момент времени, равна нулю. Нарушение такого баланса сил приводит к нарушению равновесия. Для термодинамического равновесия, в отличие от случая механического равновесия входящие в систему молекулы подвержены действию несбалансированных сил и движутся во всех возможных направлениях, если только температура не становится чрезвычайно низкой. Поэтому здесь понятие равновесия относится к некоторым коллективным характеристикам системы в целом, таким, как температура, давление или концентрация химического компонента. Пусть каждый из объектов системы, помещенной в определенную внешнюю среду, характеризуется некоторым набором характеристик, Xi и Хie соответственно. В контексте анализа равновесия следует знать об этих характеристиках их отношение к различным обменам, происходящим между системой и внешней средой. Например, если система находится в сосуде с идеально жесткими стенками, проницаемыми для тепла и непроницаемыми для вещества, то одна из этих величин, скажем X, будет совпадать с температурой и будет управлять обменом энергии в виде тепла между системой и внешней средой.

Система находится в термодинамическом равновесии, если ответственные за обмены характеристики имеют одинаковые значения в системе и во внешней среде. Для нашего примера термодинамическое равновесие между системой и внешней средой равносильно соотношению Т=Те. , справедливому в любой момент времени в любой точке системы. Поскольку стенки сосуда для вещества непроницаемы, данная система может сильно отличаться от внешней среды по своему химическому составу. С другой стороны, если сделать стенки проницаемыми для некоторых химических веществ i, то термодинамическое равновесие между системой и внешней средой наступит тогда, когда обмены этими веществами прекратятся. В простейшем случае, это означает, что соответствующие переменные, характеризующие состав системы и внешней среды, будут совпадать (сi=сiе), однако в более общем случае равновесие характеризуется равенством величин, известных под названием химических потенциалов. Совершенно аналогично, если стенки сосуда не являются жесткими, то система может обмениваться с внешней средой механической энергией. Тогда в равновесии будет иметь место также равенство давлений. При наличии внешних сил могут возникать дополнительные переменные, характеризующие термодинамическое равновесие. В качестве таких сил могут выступать, например, электрическое поле, созданное в поляризуемой среде, механическое напряжение в деформируемом материале и т. д.

В изолированных системах нет обмена ни энергией, ни веществом с внешней средой. По определению нельзя сказать, что в равновесии изолированная система находится в том же состоянии, что и внешняя среда. Но и в этом случае значительная часть высказанных соображений справедлива, поскольку некоторая небольшая часть изолированной системы испытывает действие внешней среды, которой для нее является остальная часть системы. По этой причине в равновесии различные части системы между собой термодинамически неразличимы. В соответствии с данными определениями равновесие автоматически является стационарным состоянием (δXi/δt = 0). Однако это стационарное состояние специального типа, поскольку ввиду тождественности по характеристикам Xt системе нечем обмениваться с внешней средой. Например, если равновесие обусловлено равенством температур, химических составов и давлений, то не будет систематических обменов тепловой или механической энергией, а также веществом. Это условие формулируется в виде равенства нулю полных потоков в системе: Jei = 0. Это не означает, что равновесие представляет собой некоторое совершенно застывшее состояние. Это условие следует понимать в динамическом смысле. В частности, для каждого процесса, вызывающего изменение Ji (скажем, небольшое увеличение Т по сравнению Tе в малой части системы), найдется обратный процесс, дающий противоположный вклад в Ji. Это основное свойство детального равновесия является не чем иным, как проявлением «обратимости» во времени элементарных процессов в системе, описываемой консервативными уравнениями. Именно ответственно за большинство фундаментальных свойств равновесия типа, например, единственности и устойчивости.

Рис. Схематическое представление открытой системы.

О неравновесных состояниях. Такие состояния будут связаны с неисчезающими потоками между системой и внешней средой, а также с различием в некоторых переменных состояния Xj и Xie. Эти различия могут иметь переходный характер в том смысле, что они могут мгновенно возникать благодаря некоторому начальному условию и постепенно релаксировать по мере установления равновесия между системой и внешней средой. Однако такие различия могут быть и постоянными, если создать и поддерживать соответствующие условия, которые мы будем называть ограничениями. Так, постоянная разность температур между двумя сечениями пластины или подкачка исходного реагента с одновременной эвакуацией конечного продукта в системе с химическими реакциями приведут к неравновесным ситуациям, в которых система не сможет прийти в состояние, тождественное состоянию внешней среды. Из этих примеров не следует делать вывод о том, что неравновесность представляет собой некоторое условие, искусственно наложенное умным экспериментатором. В окружающей среде имеет место неравновесные состояния типа, например, состояния биосферы, которая находится под действием потока энергии, возникающего благодаря равновесию между излучениями Солнца и Земли. Вследствие постоянного или временного действия ограничений в неравновесном состоянии детального равновесия уже нет. В результате режим неравновесного состояния приобретает способность к изменениям: небольшие локальные отклонения от него не обязательно разрушаются постоянно возникающим противодействием — они могут быть усвоены или даже усилены системой, становясь тем самым источником новообразований и разнообразия. Это свойство лежит в основе способности неравновесных систем осуществлять бифуркационные переходы к новым состояниям, и эта способность делает неравновесное состояние непохожим на любое состояние равновесия.

Нелинейность и обратные связи На эволюцию влияет изменение некоторых характерных для данной задачи параметров, которые изменяются внешними силами и называются параметрами управляющими (λ). Общий вид уравнения Cтруктура функций {Fi} специфически зависит от характера рассматриваемой системы, а также от типа протекающих в ней процессов. Несмотря на огромное разнообразие многих явлений, динамика развития похожа и можно выделить некоторые основные черты, позволяющие приступить к систематическому изучению сложных явлений. Одним из таких свойств является соответствие решения уравнений равновесию в отсутствие внешних ограничений при любом виде функций F(t). Так как стационарное состояние, то отсюда следует Для неравновесного стационарного состояния можно написать Эти соотношения налагают определенные ограничения. Например, законы эволюции должны быть таковы, чтобы выполнялось требование положительности температуры или химической концентрации, полученных как решение соответствующих уравнений.

Рассмотрим пример с двумя возможными случаями по. Пусть X будет единственной переменной состояния, k — параметр и λ представляет собой внешнее ограничение. Представим теперь, что имеет место следующая реакция (символ X используется для обозначения не только концентрации, но и самого вещества). Согласно этому механизму, переменная X удовлетворяет уравнению Отсюда следует, что стационарное состояние определяется из уравнения Или
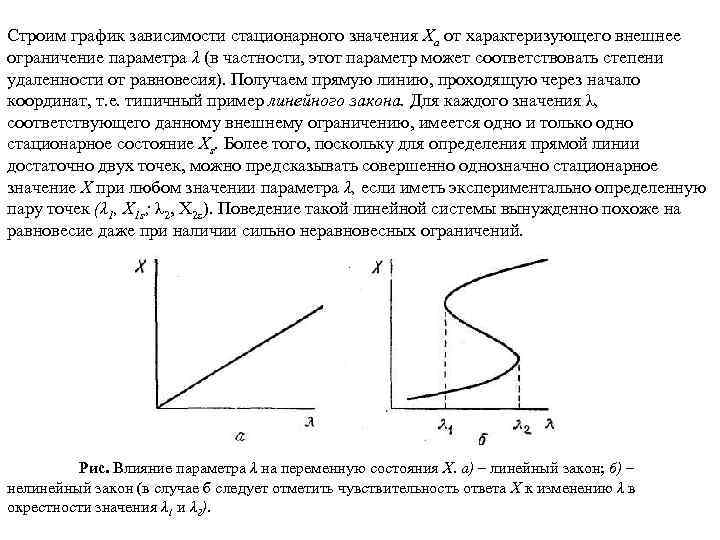
Строим график зависимости стационарного значения Ха от характеризующего внешнее ограничение параметра λ (в частности, этот параметр может соответствовать степени удаленности от равновесия). Получаем прямую линию, проходящую через начало координат, т. е. типичный пример линейного закона. Для каждого значения λ, соответствующего данному внешнему ограничению, имеется одно и только одно стационарное состояние Xs. Более того, поскольку для определения прямой линии достаточно двух точек, можно предсказывать совершенно однозначно стационарное значение X при любом значении параметра λ, если иметь экспериментально определенную пару точек (λ 1, Х 1 s; λ 2, Х 2 s). Поведение такой линейной системы вынужденно похоже на равновесие даже при наличии сильно неравновесных ограничений. Рис. Влияние параметра λ на переменную состояния Х. а) – линейный закон; б) – нелинейный закон (в случае б следует отметить чувствительность ответа Х к изменению λ в окрестности значения λ 1 и λ 2).

Рассмотрим случай соответствующий нелинейному закону ( рис. б), связывающему стационарное значение Xs с управляющим параметром λ. Когда X меньше λ 1 или больше λ 2, решение однозначно, как и на рис. а. Однако для λ 1<λ<λ 2 в системе может иметься несколько различных решений. Это качественное изменение наступает после перехода через определенное критическое значение управляющего параметра и уже позволяет понять, каким образом оказывается возможной левая или правая ориентация вращения в ячейках Бенара, равно как и во многих других случаях. Поразительное различие между линейными и нелинейными законами проявляется в применимости или нарушении принципа суперпозиции. Так, в линейных системах результатом совместного действия двух различных факторов является простая суперпозиция результатов каждого из них, взятого отдельно. Однако в нелинейных системах небольшое увеличение внешнего воздействия может привести к очень сильным эффектам, несоизмеримым по амплитуде с исходным воздействием. Примером могут служить скачки, совершаемые системой при изменении параметра λ вблизи одного из критических значений (рис. б). При недостаточной удаленности от равновесия сама по себе нелинейность не может привести к множественным решениям.

Многогранность второго закона термодинамики Нелинейность в совокупности с неравновесными ограничениями является причиной множественности решений, что ведет к диверсификации типов поведения системы. Рассмотрим как устанавливаются с течением времени решения уравнений эволюции типа. В случае диссипативных систем поиск критериев эволюции приводит к некоторым глубоким и неожиданным результатам. В самом деле, из неинвариантности уравнений для переменных состояния относительно обращения времени следует, что для таких систем характерно необратимое приближение к конечному состоянию, которое, как обычно считается, должно соответствовать независящему от времени режиму. Случай изолированных систем, в которых нет никаких обменов с внешней средой. Здесь эта тенденция к необратимости выражается вторым законом термодинамики. В соответствии с этим законом существует функция переменных состояния системы (которую мы в дальнейшем будем называть функцией состояния), изменяющаяся монотонно в процессе приближения к единственному конечному состоянию термодинамиче ского равновесия. Обычно в качестве такой функции выбирается энтропия S — величина, введенная феноменологически при изучении тепловых машин и в дальнейшем изученная на более микроскопическом уровне Больцманом, Гиббсом и другими. Формулировка второго закона имеет вид

Обычно этот закон интерпретируется как тенденция к возрастанию разупорядоченности, поскольку в микроскопической теории энтропия ассоциируется с числом допустимых состояний при определенных условиях, наложенных на систему. Отсюда вытекает, что чем меньше допустимых состояний имеет система, тем более она упорядочена. Такая интерпретация энтропии и второго закона термодинамики довольно очевидна для систем, состоящих из слабо взаимодействующих частиц. Именно к таким системам относились соображения, исходно развитые Больцманом. Например, как эксперимент, так и здравый смысл подсказывают, что газ, занимающий в начальном состоянии лишь половину ящика (рис. а), со временем перейдет к состоянию с более или менее равномерным распределением вещества по всему объему ящика (рис. б). При этом неупорядоченность увеличится, так как, вообще говоря, однородное состояние б менее структурировано, нежели исходное состояние а. Соответственно возрастет и число микроскопически эквивалентных микросостояний, поскольку объем газа в состоянии а составляет половину объема в состоянии б. Таким образом, если определить энтропию как меру числа доступных микросостояний, становится ясно, что изображенный на рис. процесс превосходно согласуется с уравнением, отражающим тенденцию к необратимому росту разупорядоченности.
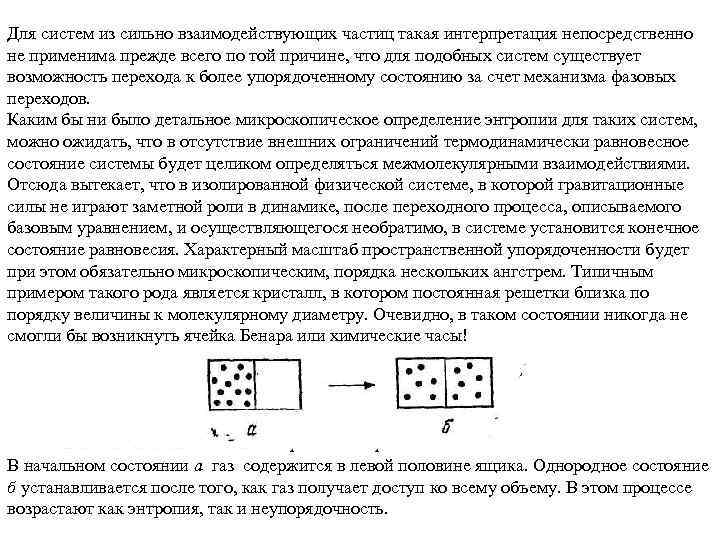
Для систем из сильно взаимодействующих частиц такая интерпретация непосредственно не применима прежде всего по той причине, что для подобных систем существует возможность перехода к более упорядоченному состоянию за счет механизма фазовых переходов. Каким бы ни было детальное микроскопическое определение энтропии для таких систем, можно ожидать, что в отсутствие внешних ограничений термодинамически равновесное состояние системы будет целиком определяться межмолекулярными взаимодействиями. Отсюда вытекает, что в изолированной физической системе, в которой гравитационные силы не играют заметной роли в динамике, после переходного процесса, описываемого базовым уравнением, и осуществляющегося необратимо, в системе установится конечное состояние равновесия. Характерный масштаб пространственной упорядоченности будет при этом обязательно микроскопическим, порядка нескольких ангстрем. Типичным примером такого рода является кристалл, в котором постоянная решетки близка по порядку величины к молекулярному диаметру. Очевидно, в таком состоянии никогда не смогли бы возникнуть ячейка Бенара или химические часы! Рис. Спонтанный переход в однородное состояние газа. В начальном состоянии а газ содержится в левой половине ящика. Однородное состояние б устанавливается после того, как газ получает доступ ко всему объему. В этом процессе возрастают как энтропия, так и неупорядочность.

Обратимся теперь к неизолированным системам, обменивающимся с внешней средой энергией или веществом. Изменение энтропии теперь представлено в виде суммы двух членов. Один из них обусловлен происходящими обменами, обозначим его de. S (поток энтропии). Другой обусловлен процессами внут ри системы, обозначим его i. S d (производство энтропии): Для изолированной системы de. S = 0, так что уравнение с учетом сводится к d. S = di. S≥ 0, т. е. к обычной формулировке второго закона. Однако даже в случае неизолированной системы член di. S будет описывать те (необратимые) процессы, которые будут попрежнему иметь место даже в отсутствие потокового члена de. S. Таким образом, приходим к следующей обобщенной форме второго закона термодинамики:

До тех пор пока di. S строго положительно, в системе будут протекать необратимые процессы, причем непрерывно. Таким образом, неравенство di. S>0 эквивалентно условию диссипативности. С другой стороны, если di. S обращается в нуль, то процесс будет обратимым и будет всего лишь захватывать соседние состояния равновесия путем медленного изменения потокового члена de. S. Именно эта последняя ситуация обычно изучается во вводных термодинамических курсах, где рассматриваются циклы Карно и различные типы тепловых машин. В число наиболее общих необратимых процессов, дающих вклад в di. S, входят химические реакции, теплопередача, диффузия, вязкая диссипация и релаксационные явления в электрически или магнитно поляризуемых системах. Для каждого из этих явлений можно определить соответствующий внутренний поток Jk, по существу отражающий скорость течения процесса, а также движущую силу Хк, отражающую имеющееся неравновесное ограничение. Замечательная особенность члена di. S состоит в том, что он является квадратичной формой по Jk и Xk, по крайней мере, для того диапазона явлений, в котором можно пользоваться локальным описанием, аналогично тому, как это имеет место в гидродинамике и химической кинетике. Эта квадратичная форма имеет вид

В таблице суммированы потоки и силы, связанные с некоторыми часто наблюдаемыми необратимыми явлениями. Таблица Термодинамические потоки и силы в некоторых часто наблюдаемых необратимых процессах

В общем случае потоки Jk являются очень сложными функциями сил. Особенно простая ситуация возникает в случае, когда эта связь линейна: В этой формуле посредством Lkl обозначен набор феноменологических коэффициентов. Такая ситуация имеет место вблизи равновесия, где, кроме того, как показано Онзагером на основе соображений, связанных с принципом детального равновесия, выполняется дополнительное соотношение Lkl = Llk. Заметим, однако, что в некоторых далеких от равновесия состояниях линейная зависимость вида все таки может иметь место. Это возможно либо благодаря случайности, либо из за наличия регуляторных процессов специального типа. Так или иначе, путем подстановки вместо фигурирующих в эволюционных (динамических) уравнениях потоков их выражений через силы и с учетом того, что сами силы линейно выражаются через переменные состояния, можно еще одним способом прийти к сформулированному уже ранее выводу о неэффективности возможных нелинейностей вблизи равновесия.

Вернемся теперь к общему виду выражения для скорости изменения энтропии. Согласно второму закону термодинамики, di. S≥ 0. Наоборот, нет такого физического закона, который определял бы знак изменения энтропии de. S в неизолированной системе (de. S≠ 0). Иными словами, в зависимости от рассматриваемой системы величина de. S может быть как положительной, так и отрицательной. Тогда понятно, что если de. S отрицательно и превышает по абсолютной величине di. S, то определенные стадии эволюции могут происходить при общем понижении энтропии: Согласно традиционной интерпретации энтропии, это будет означать, что в ходе эволюции разупорядоченность уменьшается за счет оттока энтропии. Это замечание полезно иметь в виду при выяснении природы сложных явлений, рассматривавшихся на термодинамической основе. Вопрос, однако, не так прост. Как уже подчеркивалось в первой части данного раздела, связь между энтропией и упорядоченностью довольно прозрачна в идеальных системах (в отсутствие взаимодействия между частицами), а также в случае равновесия в системах более общего характера, когда характерный пространственный масштаб возможных упорядоченных структур сравним с масштабом межмолекулярных сил. С другой стороны, та упорядоченность, которая обусловлена возникновением диссипативных структур в неравновесных условиях, совсем не обязательно должна быть напрямую связана с убылью энтропии.

Устойчивость Компоненты сложного внутренне связаны между собой. Для иллюстрации этого, рассмотрим изолированную систему и проследим связь между вторым законом термодинамики и устойчивостью. Доказано, что при любом начальном состоянии системы с течением времени в ней установится единственное состояние, состояние равновесия. С другой стороны, такая тенденция подразумевает монотонное возрастание энтропии со временем, т. е монотонное возрастание разности ΔS= S—Seq от отрицательных значений до нуля (рис. ниже). Оба эти утверждения эквивалентны, так как они выражают тот факт, что равновесие является глобальным асимптотически устойчивым состоянием, а энтропия — функцией Ляпунова, отражающей эту исключительно сильную форму устойчивости. Пусть некоторая система, консервативная или диссипативная, эволюционирующую в соответствии с определенными динамическими законами, выражается, например, уравнениями
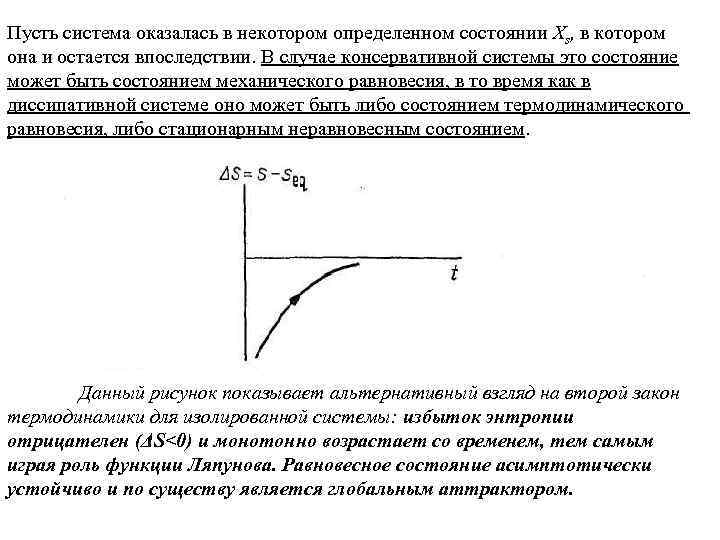
Пусть система оказалась в некотором определенном состоянии Xs, в котором она и остается впоследствии. В случае консервативной системы это состояние может быть состоянием механического равновесия, в то время как в диссипативной системе оно может быть либо состоянием термодинамического равновесия, либо стационарным неравновесным состоянием. Данный рисунок показывает альтернативный взгляд на второй закон термодинамики для изолированной системы: избыток энтропии отрицателен (ΔS<0) и монотонно возрастает со временем, тем самым играя роль функции Ляпунова. Равновесное состояние асимптотически устойчиво и по существу является глобальным аттрактором.

На самом деле состояние реальных систем никогда не остается постоянным. Большинство систем контактирует со сложным и даже непредсказуемым окружением, которое непрерывно сообщает системе небольшие (реже значительные) количества вещества, импульса или энергии, что делает невозможным контроль любой из переменных состояния со сколь угодно высокой степенью точности. Любой экспериментатор в той или иной мере знаком с этими трудностями, и классические выражения «экспериментальная погрешность» или «доверительный интервал» являются просто отражением вмешательства внешней среды во внутреннюю динамику системы. Этот вездесущий факт выражается в том, что мгновенное состояние X(t) системы не совпадает со стационарным состоянием Xs — оно представляет собой некоторое соседнее состояние: Величина x(t) называется возмущением.

Другая, более фундаментальная точка зрения на ту же проблему. Большинство систем, с которыми мы имеем дело, состоит из огромного числа взаимодействующих объектов. Для таких систем переменные состояния, следует понимать в статистическом смысле. Это означает, что такие переменные представляют собой либо средние значения по мгновенным состояниям на длинном временном интервале, либо возможно, наиболее вероятные значения которые могут приниматься этими переменными. Поэтому в действительности регистрация мгновенного состояния показала бы наличие отклонений от таких «стандартных» значений макроскопических переменных состояния. Такие внутренние отклонения (флуктуации) генерируются системой спонтанно независимо от "внешней среды. Их влияние можно выразить равенством (а) при том понимании, что x(t) теперь обусловлено внутренней динамикой рассматриваемой системы. Обычно флуктуация возникает в виде локализованного, маломасштабного события. Например, в некоторой малой части макроскопической системы определенные частицы могут иметь большую тепловую скорость по сравнению с их соседями. Потом плотность частиц в каком то другом малом объеме может оказаться пониженной и т. д. Легко понять, что такие события являются случайными. Это свойство отражается терминами типа «фоновый шум» , часто используемыми для обозначения флуктуации.

Имеются причины, по которым состояние системы будет непрерывно отклоняться от стандартного состояния Ха. Рассмотрим, каким образом система отвечает на такие отклонения. Имеется полный список всех возможных вариантов случаев. Случай 1. Состояние X(t) остается в некоторой окрестности стандартного состояния Xs на всех временах, превышающих некоторое начальное время to. Точнее, при любом наперед заданном ε>0 всегда найдется такое δ, зависящее в общем случае от ε и to, что при начальном возмущении, не превышающем δ, отклонение x(t) остается меньше ε на всех временах, превышающих to. Мы будем тогда говорить, что состояние Xs устойчиво по Ляпунову. Это понятие иллюстрируется тремя альтернативными способами на рис. Во многих случаях нас интересует не ответ какого то данного состояния на возмущения, но скорее ответ целой последовательности состояний, определяющей некоторую траекторию. В этом случае вводится подходящая мера расстояния между стандартной и возмущенной траекториями, после чего используется упомянутое выше определение устойчивости. Это приводит к понятию орбитальной устойчивости

Случай 2. (асимптотическая устойчивость). Состояние X(t) стремится к Xs по мере того, как время стремится к бесконечности, или, иными словами, возмущение x(t) со временем стремится к нулю. Тогда мы говорим, что состояние Xs является асимптотически устойчивым (рис. а) Это определение можно обобщить на асимптотическую орбитальную устойчивость. Ясно, что асимптотическая устойчивость обязательно подразумевает необратимость, так что это понятие неприменимо к консервативным системам. Такие системы в лучшем случае могут быть устойчивыми по Ляпунову. С другой стороны, диссипативные системы могут устранять влияние возмущений, действующих на их, и тем самым восстанавливать стандартное состояние. Это обеспечивает предсказуемость и воспроизводимость такого режима, который в дальнейшем будем называть аттрактором (например, ячейки Бенара, колебания в реакции БЖ или состояние термодинамического равновесия в изолированной системе). Асимптотическая устойчивость одно из наиболее ярких проявлений конструктивной роли необратимости в природе.
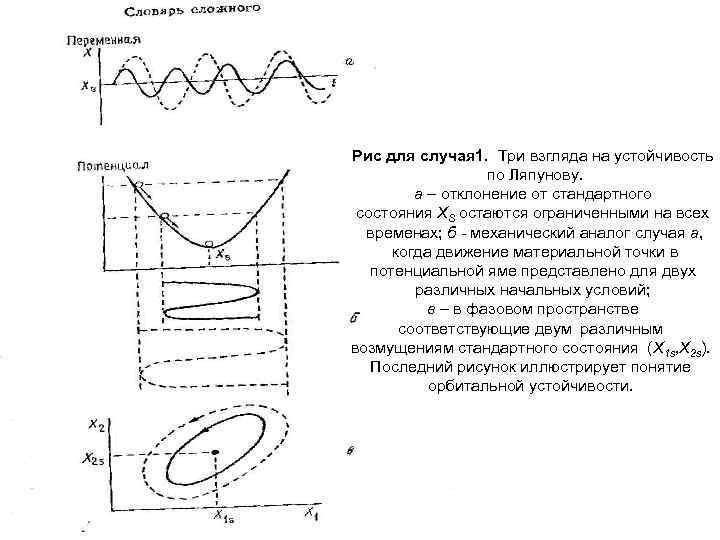
Рис для случая 1. Три взгляда на устойчивость по Ляпунову. а – отклонение от стандартного состояния XS остаются ограниченными на всех временах; б - механический аналог случая а, когда движение материальной точки в потенциальной яме представлено для двух различных начальных условий; в – в фазовом пространстве соответствующие двум различным возмущениям стандартного состояния (X 1 s, X 2 s). Последний рисунок иллюстрирует понятие орбитальной устойчивости.
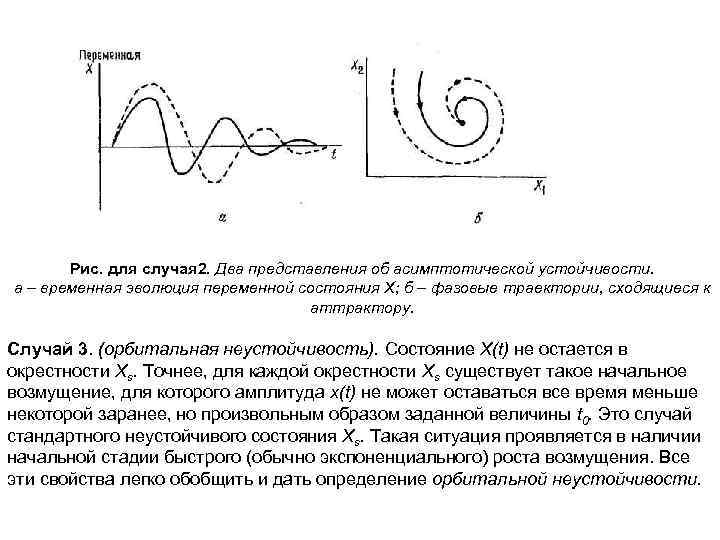
Рис. для случая 2. Два представления об асимптотической устойчивости. а – временная эволюция переменной состояния Х; б – фазовые траектории, сходящиеся к аттрактору. Случай 3. (орбитальная неустойчивость). Состояние X(t) не остается в окрестности Xs. Точнее, для каждой окрестности Xs существует такое начальное возмущение, для которого амплитуда x(t) не может оставаться все время меньше некоторой заранее, но произвольным образом заданной величины t 0. Это случай стандартного неустойчивого состояния Хs. Такая ситуация проявляется в наличии начальной стадии быстрого (обычно экспоненциального) роста возмущения. Все эти свойства легко обобщить и дать определение орбитальной неустойчивости.
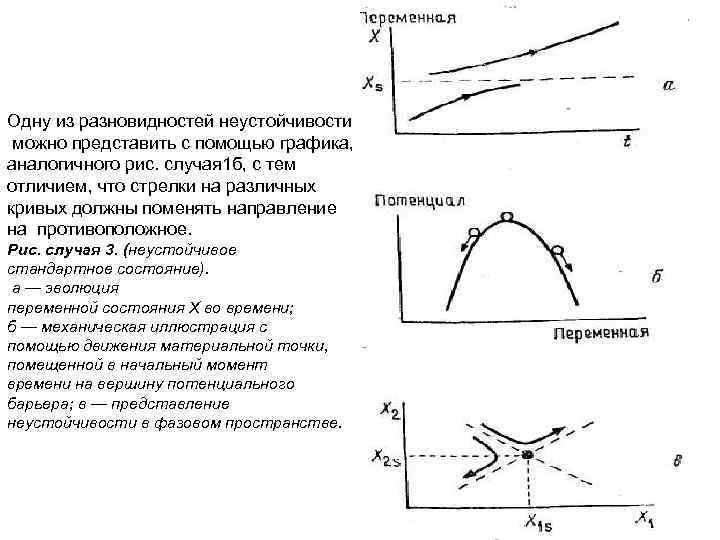
Одну из разновидностей неустойчивости можно представить с помощью графика, аналогичного рис. случая 1 б, с тем отличием, что стрелки на различных кривых должны поменять направление на противоположное. Рис. случая 3. (неустойчивое стандартное состояние). а — эволюция переменной состояния X во времени; б — механическая иллюстрация с помощью движения материальной точки, помещенной в начальный момент времени на вершину потенциального барьера; в — представление неустойчивости в фазовом пространстве.

Неустойчивые стандартные состояния могут встретиться как в консервативных, так и в диссипативных системах. Примерами такого рода служат верхнее положение равновесия маятника и состояние покоя в задаче Бенара выше порога возникновения конвекции. Однако, в то время как в случае диссипативной системы особых ограничений нет, состояние консервативной системы должно остаться неустойчивым и после обращения времени. Это замечание находится в согласии с рис. а, в, но противоречит рис. б с обращенными стрелками. Случай 4. (случай равновесия устойчивого локально и неустойчивого глобально). Состояние X(t) остается в некоторой окрестности стандартного состояния Xs, если начальные возмущения не превышают некоторого порогового значения, и удаляется от него в случае возмущений, превышающих пороговое. Тогда мы говорим, что состояние Xs локально устойчиво, но глобально неустойчиво. С другой стороны, если устойчивость имеет место при любых по амплитуде начальных возмущениях, мы говорим о глобальной устойчивости, причем состояние Xs в таком случае является глобальным аттрактором. Например, термодинамическое равновесие в изолированной системе является глобальным аттрактором, однако состояние конвекции в задаче Бенара, для которого течение в определенной ячейке ориентировано по часовой стрелке, глобально неустойчиво по отношению к конечному возмущению, меняющему ориентацию течения в той же ячейке.
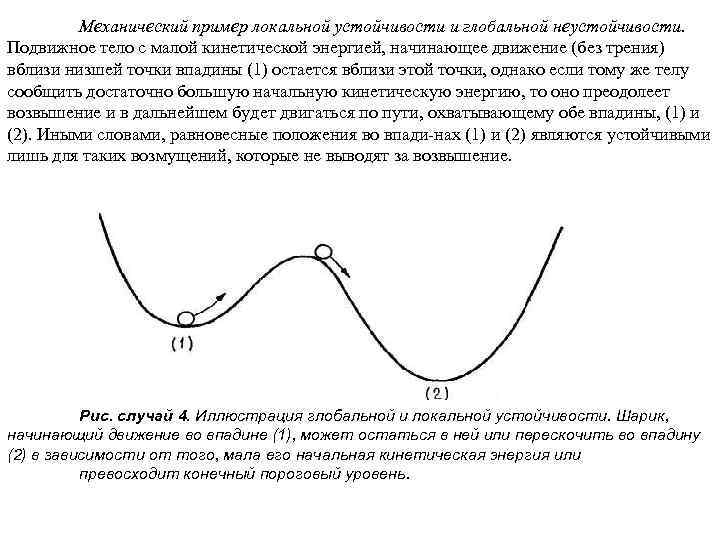
Механический пример локальной устойчивости и глобальной неустойчивости. Подвижное тело с малой кинетической энергией, начинающее движение (без трения) вблизи низшей точки впадины (1) остается вблизи этой точки, однако если тому же телу сообщить достаточно большую начальную кинетическую энергию, то оно преодолеет возвышение и в дальнейшем будет двигаться по пути, охватывающему обе впадины, (1) и (2). Иными словами, равновесные положения во впади нах (1) и (2) являются устойчивыми лишь для таких возмущений, которые не выводят за возвышение. Рис. случай 4. Иллюстрация глобальной и локальной устойчивости. Шарик, начинающий движение во впадине (1), может остаться в ней или перескочить во впадину (2) в зависимости от того, мала его начальная кинетическая энергия или превосходит конечный пороговый уровень.

Некоторые выводы. Анализируя устойчивость, можно теперь легче понять концептуальный прогресс, достигнутый при переходе от изолированных систем, для которых справедливо соотношение d. S/dt≥ 0, к «открытым системам вдали от равновесия. В изолированной системе равновесие глобально устойчиво (устойчивость по Ляпунову), и это отражается в существовании некоторой функции — энтропии, или, точнее, избыточной энтропии обладающей свойствами. Эти соотношения равносильны глобальной устойчивости. В неизолированной системе, не находящейся в состоянии равновесия, вследствие наличия двух членов в выражении для баланса энтропии (de. S и di. S) второй закон термодинамики (di. S /dt≥ 0) больше не определяет знак изменения энтропии (то же справедливо и для любой другой функции состояния). Таким образом, универсальной функции Ляпунова не существует, и это порождает проблему устойчивости состояний, далеких от равновесия. Возможность потери устойчивости при определенных условиях открывает путь переходным явлениям, что может привести к внутренней дифференциации и сложному поведению.

Имеется одно исключение — открытые системы вблизи равновесия. Поскольку в этой области феноменологические соотношения линейны и кинетические коэффициенты симметричны, выражаемое равенством производство энтропии становится положительно определенной квадратичной формой переменных состояния Хk, отражающих внешние ограничения. Можно показать, что любое отклонение от стационарного состояния приводит к развитию таких процессов, что величина di. S/dt стремится уменьшиться со временем. Иными словами, ситуация здесь аналогична случаю4, причем в этой ситуации производство энтропии играет роль функции Ляпунова, гарантируя глобальную устойчивость стационарных состояний, близких к равновесному. Нет общего закона, гарантирующего устойчивость состояний, далеких от равновесия. Тем не менее можно найти некоторые полезные критерии, позволяющие сделать более слабые выводы типа, например, достаточных условий устойчивости. Один такой критерий дается условием положительности избыточного производства энтропии, вычисленного вблизи неравновесного стандартного состояния.

Бифуркация и нарушение симметрии Рассмотрим задачу Бенара. Важна роль нелинейностей и внешних ограничений, управляющих поведением системы вдали от равновесия. Рис. Диаграмма бифуркации, показывающая влияние изменения управляющего параметра на переменную состояния X. Единственное решение (а), соответствующее термодинамической ветви, теряет устойчивость при λс. При этом значении управляющего параметра появляются новые ветви решения (b 1, b 2) которые в данном случае устойчивы.

Известно, что при изменении управляющих параметров в системе наблюдаются разнообразные переходные явления. Выделим теперь из этих наблюдений определенные общие черты, характерные для большого числа других переходов в физико химических системах. С этой целью представим графически (рис. ) зависимость вертикальной компоненты скорости течения жидкости в некоторой определенной точке от внешнего ограничения, «или, в более общем виде, зависимость переменной состояния системы X (или х=Х—Xs) от управляющего параметра λ. Полученный график называется бифуркационная диаграмма. При малых значениях λ возможно лишь одно решение, соответствующее состоянию покоя в бенаровском эксперименте. Оно представляет собой непосредственную экстраполяцию термодинамического равновесия, подобно равновесию, характеризуется важным свойством — асимптотической устойчивостью, поскольку в этой области система способна гасить внутренние флуктуации или внешние возмущения. По этой причине такую ветвь состояний мы будем называть термодинамической ветвью. При переходе через критическое значение параметра λ, обозначенное λс на рисунке , состояния на этой ветви становятся неустойчивыми, так как флуктуации или малые значение возмущения уже не гасятся. Действуя подобно усилителю, система отклоняется от стандартного состояния и переходит к новому режиму, в случае бенаровского эксперимента соответствующему состоянию стационарной конвекции. Оба этих режима сливаются при λ=λс и различаются при λ>λс. Это явление называется бифуркацией.

Это явление следует ассоциировать с катастрофическими изменениями и конфликтами; в решающий момент перехода система должна совершить критический выбор (в окрестности λ=λС), что в задаче Бенара связано с возникновением право или лево вращательных ячеек в определенной области пространства (рис. ветви b 1 или b 2). В устройстве экспериментальной установки нет ничего такого, что позволило бы наблюдателю определить заранее, какое состояние будет выбрано. Решать будет лишь случай через динамику флуктуации. Просканировав «фон» , система совершит несколько попыток, поначалу, возможно, безуспешных, и наконец, какая то особенная флуктуация победит. Стабилизировав ее, система превращается в своеобразный исторический объект в том смысле, что его дальнейшая эволюция будет зависеть от этого критического выбора. Таким образом, можно на абстрактном языке сформулировать замечательное взаимодействие между случаем и внешним ограничением, между флуктуациями и необратимостью, лежащее в основе большинства явлений. Можно отметить сходство между этими представлениями и понятиями мутации и отбора, известными из теории биологической эволюции. На самом деле можно сказать, что флуктуации являются физическим аналогом мутантов, в то время как поиск устойчивости играет роль естественного отбора.
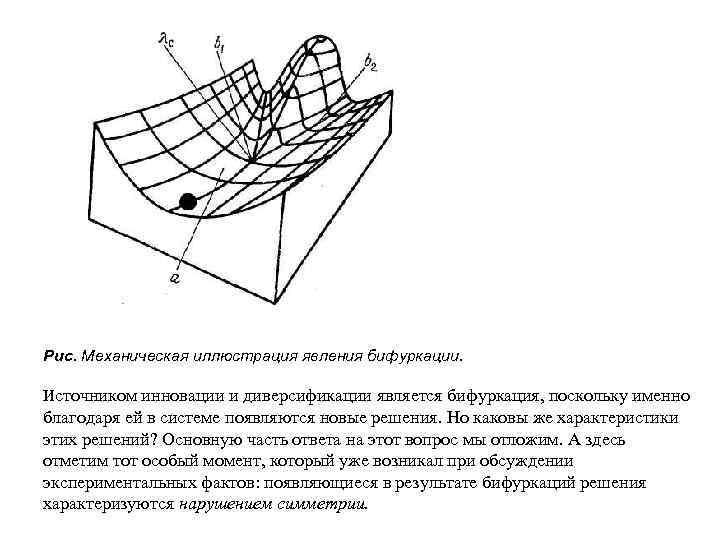
Рис. Механическая иллюстрация явления бифуркации. Источником инновации и диверсификации является бифуркация, поскольку именно благодаря ей в системе появляются новые решения. Но каковы же характеристики этих решений? Основную часть ответа на этот вопрос мы отложим. А здесь отметим тот особый момент, который уже возникал при обсуждении экспериментальных фактов: появляющиеся в результате бифуркаций решения характеризуются нарушением симметрии.

Путем наблюдений установлено, что определенные физические явления допускают совершенно одинаковое описание даже в том случае, когда экспериментальные наблюдения проводятся в различных условиях. Например, ниже порога бенаровской конвекции сосуд с жидкостью имеет идентичные свойства для всех наблюдателей, смещенных друг относительно друга вдоль определенного направления (трансляционная инвариантность). Законы, описывающие эти явления, должны характеризоваться определенной симметрией, допускающей соответствующую инвариантность этих явлений. Эти виды симметрии должны сохраняться при всех пространственных и временных операциях, меняющих местами наблюдателей, для которых данный вид инвариантности возможен. Довольно часто эти операции образуют некоторый математический объект, называемый группой, поскольку последовательное выполнение нескольких таких операций эквивалентно некоторой новой операции, что уже само по себе сходно с инвариантностью. Так, динамические уравнения, описывающие жидкость, нагреваемую снизу и содержащуюся между двумя пластинами, бесконечно протяженными в горизонтальном направлении, инвариантны относительно группы трансляций вдоль любой горизонтальной плоскости. Аналогичным образом уравнения химической кинетики в бесконечно протяженной среде инвариантны относительно групп трансляций, вращений и отражений.

И все же, несмотря на исключительную симметрию этих динамических законов, экспериментально наблюдается возникновение таких состояний, как ячейка Бенара или химическая волна, причем каждое из этих состояний менее симметрично, нежели сами законы. Этот переход с нарушением симметрии возник благодаря бифуркации. Что же достигнуто в результате такого перехода? Нарушение симметрии является проявлением внутренней дифференциации между различными частями системы или между системой и ее окружением. Нарушение симметрии воплощает одну из первейших предпосылок сложного поведения, которая должна была реализоваться при таких событиях, как сгущение первичной материи при образовании галактик или возникновение первых живых клеток. Кроме того, как только такая дифференциация обеспечена, могут включаться другие процессы, невозможные в недифференцированной среде. Например, возникновение пространственных неоднородностей в биологической среде может дать недифференцированным клеткам в популяции возможность распознавать окружающую их среду и дифференцироваться в специализированные клетки. В свою очередь это может позволить генетическому материалу проявить свои потенциальные возможности. Следовательно, нарушение симметрии оказывается также предпосылкой информации. Но не следует забывать, что между предпосылкой и достаточным условием довольно большое расстояние. Переходы с нарушением симметрии имели бы большое значение лишь в том случае, если бы они могли привести к асимптотически устойчивым решениям. Помимо прочего, необходимо иметь возможность тем или иным способом отбирать конкретную асимметричную форму материи из всего множества решений, становящихся одновременно возможными выше точки бифуркации.

Упорядоченность и корреляции Термодинамическое равновесие— это состояние с микроскопическими характерными пространственными масштабами, а возникающие вдали от равновесия переходные явления связаны с состояниями, характеризуемыми корреляциями в макроскопическом диапазоне. И если первое представляется вполне естественным с точки зрения короткодействующих межмолекулярных сил, то второе, наоборот, весьма поражает с той же точки зрения. Этот кажущийся парадокс еще больше усиливается, если учесть, что неравновесные переходы, когерентно охватывающие макроскопические области пространства, могут иметь место даже в идеальных системах, в которых можно полностью пренебречь межмолекулярными взаимодействиями.
Базовые понятия синергетики.ppt