Базовая искусственная модель Каждый входной сигнал проходит через

Базовая искусственная модель Каждый входной сигнал проходит через соединение, имеющее определенную интенсивность (или вес); этот вес соответствует синаптической активности биологического нейрона. С каждым нейроном связано определенное пороговое значение. Вычисляется взвешенная сумма входов, из нее вычитается пороговое значение и в результате получается величина активации нейрона. , j=0. . . m-1

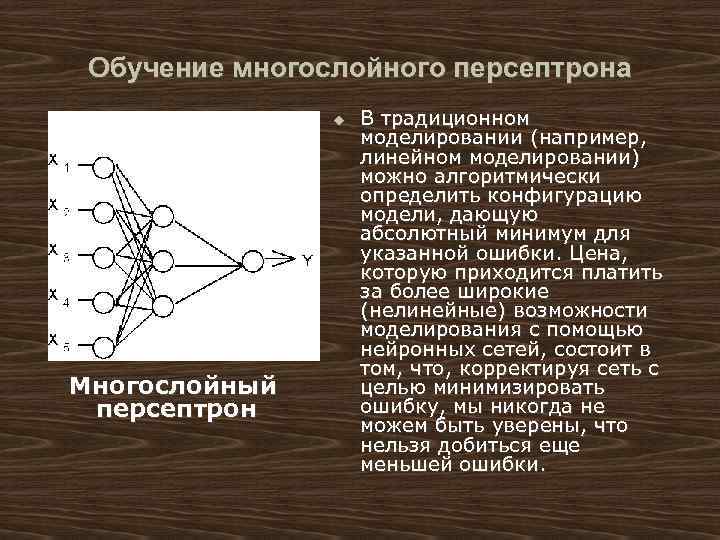
Обучение многослойного персептрона u Многослойный персептрон В традиционном моделировании (например, линейном моделировании) можно алгоритмически определить конфигурацию модели, дающую абсолютный минимум для указанной ошибки. Цена, которую приходится платить за более широкие (нелинейные) возможности моделирования с помощью нейронных сетей, состоит в том, что, корректируя сеть с целью минимизировать ошибку, мы никогда не можем быть уверены, что нельзя добиться еще меньшей ошибки.

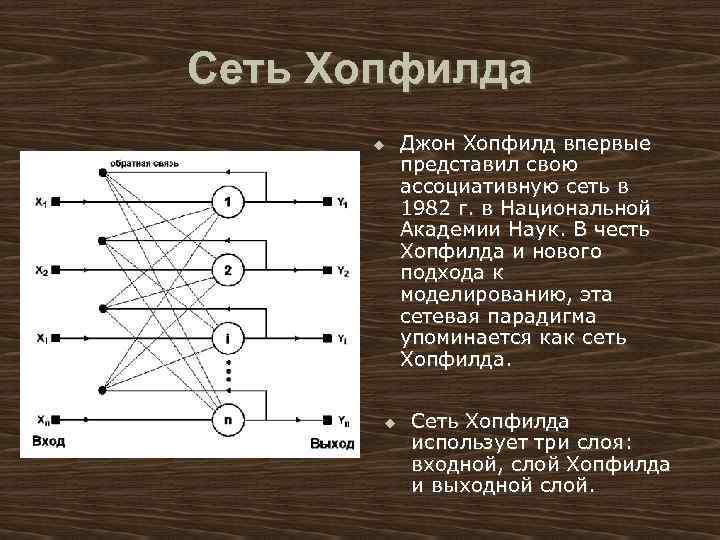
Сеть Хопфилда u u Джон Хопфилд впервые представил свою ассоциативную сеть в 1982 г. в Национальной Академии Наук. В честь Хопфилда и нового подхода к моделированию, эта сетевая парадигма упоминается как сеть Хопфилда. Сеть Хопфилда использует три слоя: входной, слой Хопфилда и выходной слой.

Ассоциативная память Различают автоассоциативную и гетероассоцнативную память. В обоих случаях имеется режим записи и режим воспроизведения. В случае автоассоциативной памяти при записи происходит запоминание набора эталонных образов, задаваемых векторами Хk, k=1, 2, . . . , n; а при воспроизведении по искаженному образу Xj + δХ (Xj - один из эталонов, δХ вектор, характеризующий искажение) восстанавливается эталон Хj. В случае гетероассоциативиой памяти нейронная сеть при записи запоминает отображение Хk-->Yk между векторами Хk и Yk, k=1, 2, . . , n; при воспроизведении предъявляется один из эталонных векторов Xj (возможно несколько искаженный), и с помощью нейронной сети восстанавливается парный ему вектор Yj.

Сеть Хопфилда Допустим, что имеется некоторая физическая система, имеющая множество устойчивых особых точек: Х 1, Х 2, . . . Эти точки могут рассматриваться как память устройства, реализуемого физической системой. Начиная с некоторой точки Xj + δХ (Xj -один из эталонов, δХ - вектор, характеризующий искажение), при малом δХ мм придем к Xj. Это вариант автоассоциативной памяти, в которой запомненный образ восстанавливается по искаженному образу. Удобно построить физическую систему, имеющую локальные минимумы энергии, соответствующие устойчивым особым точкам. Для того чтобы систему можно было бы рассматривать как намять, нужно иметь большое число локальных минимумов. Пример физической системы с большим числом локальных минимумов энергии — спиновые стекла, т. е. система спинов, матрица обменных взаимодействий между которыми стохастичиа. Хопфилд строит модель нейроподобной ассоциативной памяти, допускающую проведение явных аналогий со спиновыми стеклами. Опишем в общих чертах эту модель

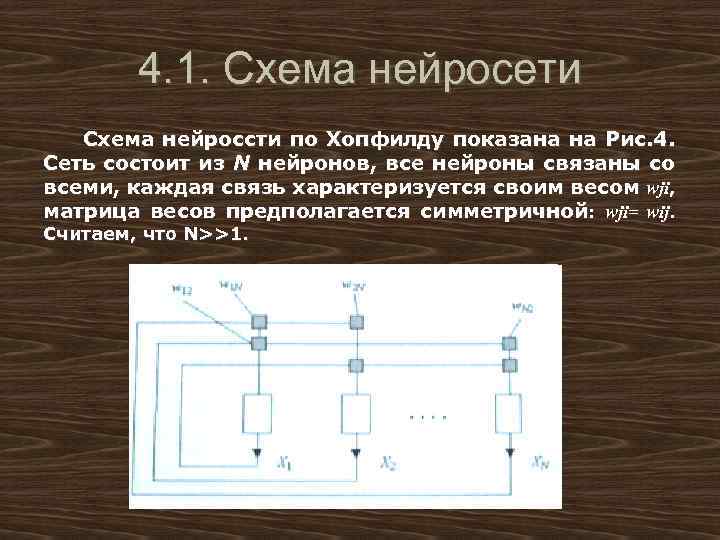
4. 1. Схема нейросети Схема нейроссти по Хопфилду показана на Рис. 4. Сеть состоит из N нейронов, все нейроны связаны со всеми, каждая связь характеризуется своим весом wji, матрица весов предполагается симметричной: wji= wij. Считаем, что N>>1.

Рис. 4. Схема нейронной сети по Хофилду. - нейроны, - синапсы Состояние нейронной сети характеризуется вектором X = Х 1, Х 2, . . . , XN, Каждый нейрон может находиться в двух состояниях Xi=0 - покой, Xi=1 возбужденное состояние, i - номер нейрона.

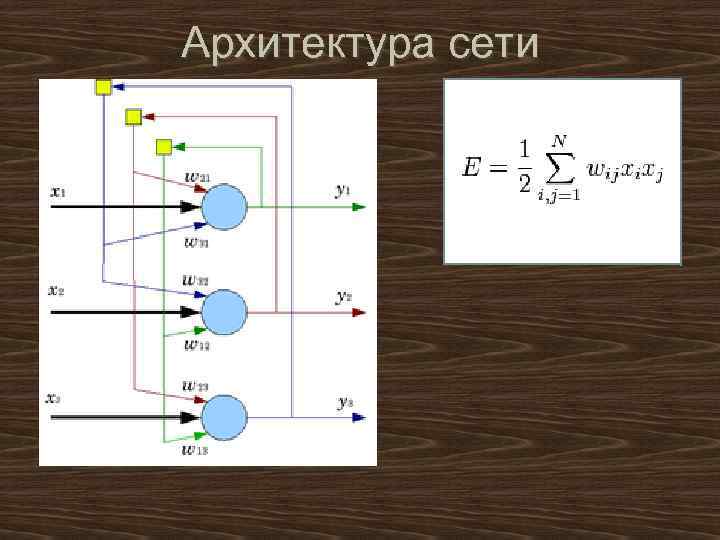
Архитектура сети

u На стадии инициализации сети весовые коэффициенты синапсов (связей, по которым выходные сигналы одних нейронов поступают на входы других) устанавливаются следующим образом: Где i и j ()– индексы, соответственно, предсинаптического (входного) и постсинаптического (выходного) нейронов; wij — i-й синаптический вес j-го нейрона; xik, xjk – i-ый и jый элементы вектора k-ого образца.

u На входы сети подаётся неизвестный сигнал. Фактически его ввод осуществляется непосредственной установкой значений: yj(0) = xj , j = 0. . . n-1, где yj — аксон (т. е. выход) j-го нейрона. Поэтому обозначение на схеме сети входных синапсов в явном виде носит чисто условный характер. Ноль в скобке справа от yj означает нулевую итерацию в цикле работы сети.

Рассчитывается новое состояние нейронов и новые значения аксонов: u Рассчитывается новое состояние нейронов и новые значения аксонов: где j=0. . . n-1, p – номер (конкретный шаг) итерации

u новое состояние нейрона где f – активационная функция в виде скачка

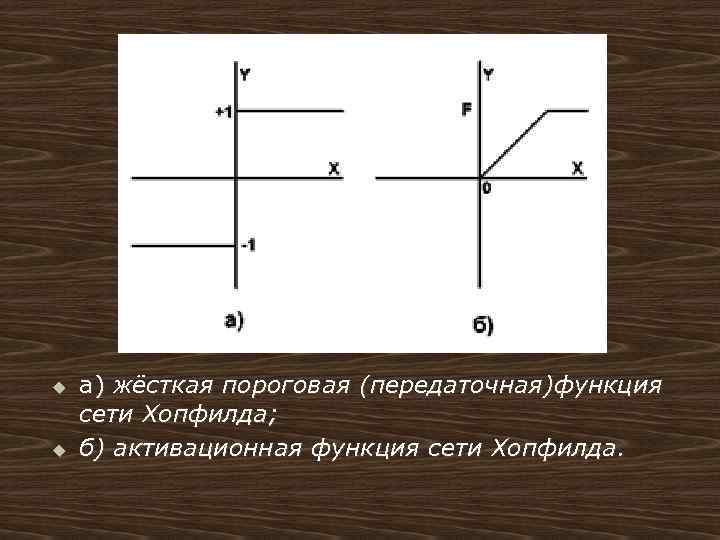
u u а) жёсткая пороговая (передаточная)функция сети Хопфилда; б) активационная функция сети Хопфилда.

Конец алгоритма u Проверка: изменились ли выходные значения аксонов за последнюю итерацию. Если да – переход к пункту 2, иначе (если выходы застабилизировались) – конец. При этом выходной вектор представляет собой образец, наилучшим образом сочетающийся с входными данными.

Работу нейронной сети в режиме воспроизведения можно рассматривать как динамическую систему. Покажем, что если число эталонов не слишком высоко, то эталоны соответствуют устойчивым состояниям (особым точкам) рассматриваемой динамической системы. Оценим величину netsj=Σiwji. Xsi(t), (7) где Xsi(t)-компоненты какого-либо эталонного вектора. С учетом (4) имеем: netsj= Σk(2 Xki-1)[Σi(2 Xkj-1) Xsi(t)]. (8) В силу случайности эталонов среднее значение величины в квадратных скобках равно 0 при s≠k и равно N/2 при s=k. Следовательно, в силу такой псевдоортогональности имеем: netsj≈(2 Xsj-1)N/2 (9) Итак, имеем: netsj > 0 при Xsj=1 и netsj < 0 при Xsj=0. Следовательно, в пренебрежении шумом, возникающим от случайных флуктуации, запомненные эталоны устойчивы.

Минимизация энергии нейронной сети Определим "энергию" нейронной сети как E=-0, 5Σijwji. Xj, i≠j (10) Так как wji=wij, то изменение энергии, обусловленное текущим изменением состояния нейрона, равно ∆E=-∆XjΣijwji. Xi= -∆Xjnetj, i≠j (11) В силу (5) ∆E≤ 0. Таким образом, алгоритм изменения состояний нейронов приводит к монотонному уменьшению энергии. Состояния изменяются до тех пор. пока не будет достигнут локальный минимум энергии. Энергия играет роль функции Ляпунова для рассматриваемой динамической системы. Из (9), (11) следует, что эталоны соответствуют минимумам энергии Е.

u u Алгоритм обучения сети Хопфилда имеет существенные отличия в сравнении с такими классическими алгоритмами обучения перцептронов как метод коррекции ошибки или метод обратного распространения ошибки. Отличие заключается в том, что вместо последовательного приближения к нужному состоянию с вычислением ошибок, все коэффициенты матрицы рассчитываются по одной формуле, за один цикл, после чего сеть сразу готова к работе. Вычисление коэффициентов базируется на следующем правиле: для всех запомненных образов Xi матрица связи должна удовлетворять уравнению:

u Некоторые авторы относят сеть Хопфилда к обучению без учителя. Но это неверно, т. к. обучение без учителя предполагает отсутствие информации о том, к каким классам нужно относить тот или иной образ. Для сети Хопфилда без этой информации нельзя настроить весовые коэффициенты, поэтому здесь можно говорить лишь о том, что такую сеть можно отнести к классу оптимизирующих сетей (фильтров). Отличительной особенностью фильтров является то, что матрица весовых коэффициентов настраивается детерминированным алгоритмом раз и навсегда, и затем весовые коэффициенты больше не изменяются.

u весовая матрица W может быть найдена вычислением внешнего произведения каждого запоминаемого вектора с самим собой и суммированием матриц, полученных таким образом. Это может быть записано в виде

Обработка данных сетью Хэмминга

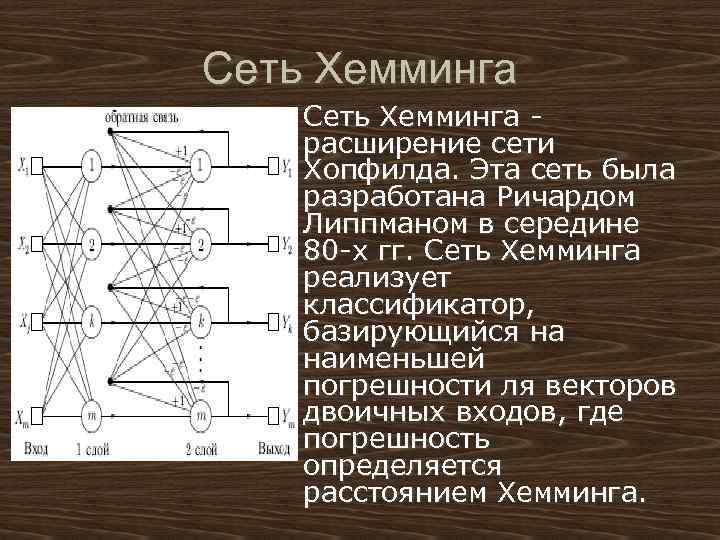
Сеть Хемминга u Сеть Хемминга - расширение сети Хопфилда. Эта сеть была разработана Ричардом Липпманом в середине 80 -х гг. Сеть Хемминга реализует классификатор, базирующийся на наименьшей погрешности ля векторов двоичных входов, где погрешность определяется расстоянием Хемминга.

u u Сеть состоит из двух слоев. Первый и второй слои имеют по m нейронов, где m – число образцов. Нейроны первого слоя имеют по n синапсов, соединенных со входами сети (образующими фиктивный нулевой слой). Нейроны второго слоя связаны между собой ингибиторными (отрицательными обратными) синаптическими связями. Единственный синапс с положительной обратной связью для каждого нейрона соединен с его же аксоном. Идея работы сети состоит в нахождении расстояния Хэмминга от тестируемого образа до всех образцов. Расстоянием Хэмминга называется число отличающихся битов в двух бинарных векторах. Сеть должна выбрать образец с минимальным расстоянием Хэмминга до неизвестного входного сигнала, в результате чего будет активизирован только один выход сети, соответствующий этому образцу.

Алгоритм функционирования сети Хемминга u 1. На стадии инициализации весовым коэффициентам первой слоя и порогу передаточной функции присваиваются такие значения: u Wik=x. Ik/2, i=0. . . n-1, k=0. . . m-1 u bk = n/2, k = 0. . . m-1 u Здесь xik - i-ый элемент k-ого образца.

Алгоритм функционирования сети Хемминга u u u 2. На входы сети подается неизвестный вектор x 1, xi, xn. . . Рассчитываются состояния нейронов первого слоя (верхний индекс в скобках указывает номер слоя): , j=0. . . m-1 После этого получения значения инициализируют значения выходов второго слоя: yj(2) = yj(1), j = 0. . . m-1

Алгоритм функционирования сети Хемминга u u u 3. Вычисляются новые состояния нейронов второго слоя: и значения их выходов: Yj (1)(t+1)=f|S j(2)(t+1)|

Алгоритм функционирования сети Хемминга 4. Проверяется, изменились ли выходы нейронов второго слоя за последнюю итерацию. Если даперейти к шагу 3. u Иначе - конец u

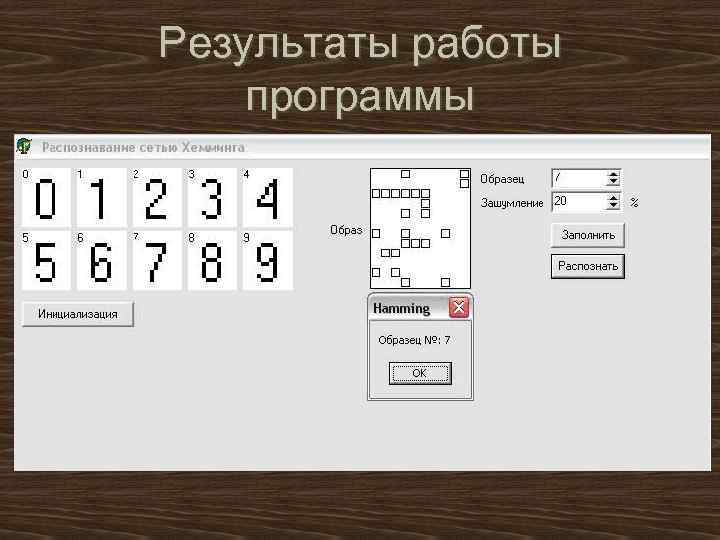
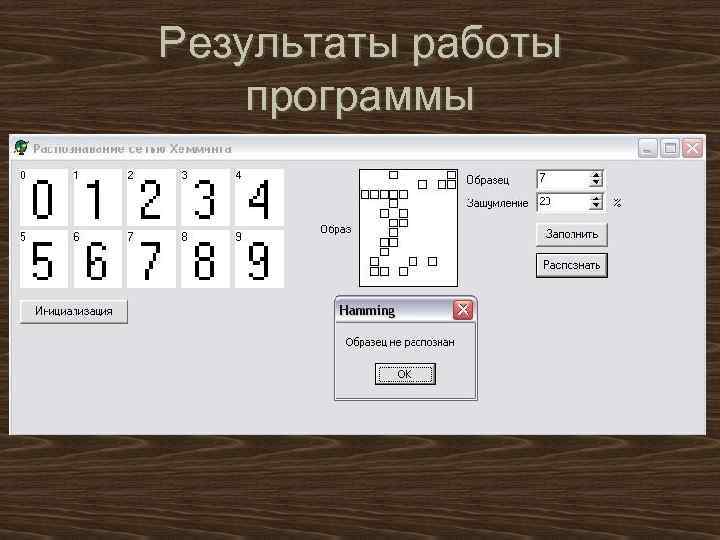
Результаты работы программы

Статистика распознавания Процент шума 0% 5% 10% 15% 20% Процент Распознавания Глазом 100% 80% 40% 30% 1% Процент Распознавания Компьютером 90% 80% 80% 70% Процент Ошибочного распознавания 0% 0% 0% 10% Процент нераспознаван ия 10% 20%

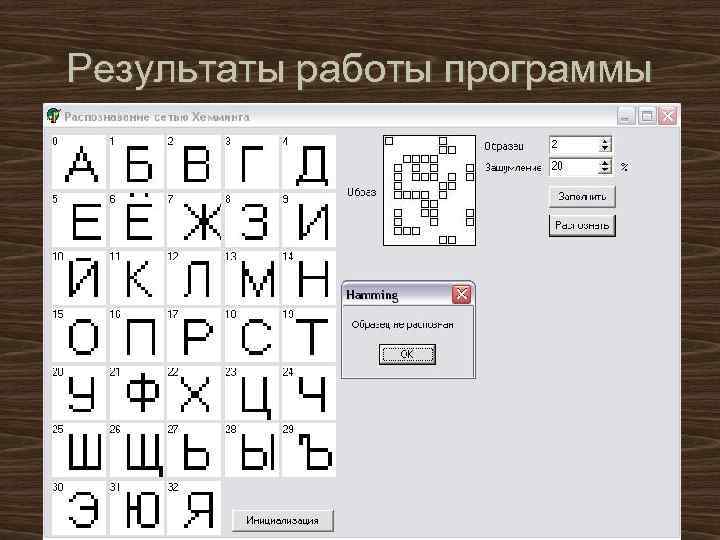
Результаты работы программы

Статистика распознавания Процент шума 0% 5% 10% 15% 20% Процент Распознавания Глазом 100% 85% 43% 1% Процент Распознавания Компьютером 80% 75% 68% 60% Процент Ошибочного распознавания 0% 0% 0% 10% Процент нераспознавания 20% 25% 22% 30%

Заключение u Нами был произведен анализ теории нейронных сетей и возможности их применения в моделировании ассоциативной памяти и поиска. Делая вывод из результатов проделанной нами практической работы мы можем сказать, что метод распознавания текста с помощью нейронных сетей успешно может применяться при зашумленности входного сигнала от 10 до 25%.