af5d3050bfe83e2ecbda9608d2106dde.ppt
- Количество слайдов: 30

Bayesian Probability theory in astronomy: Timing analysis of Neutron Stars VII BSAC, Chepelare, Bulgaria, 01. 06. 2010 Valeri Hambaryan Astrophysical Institute and University Observatory, Friedrich Schiller University of Jena, Germany E-Mail: vvh@astro. uni-jena. de 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan

Outline of talk • Introduction • Method • Results & Outlook BSAC VII, 01. 06. 2010, V. Hambaryan
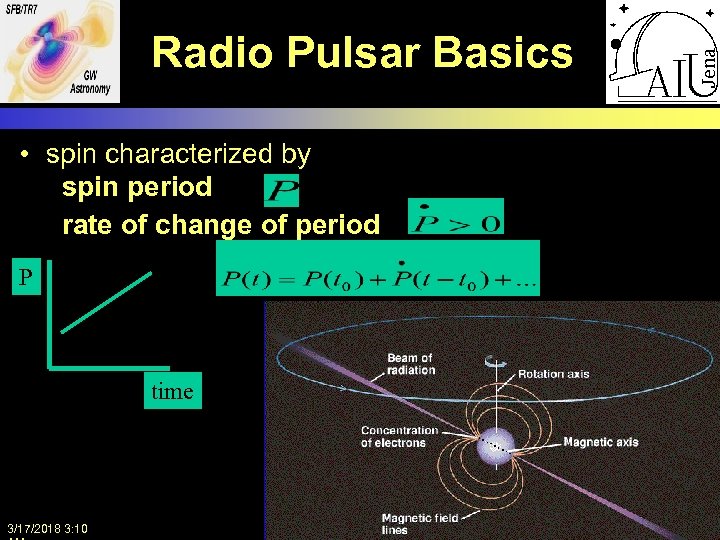
Radio Pulsar Basics • spin characterized by spin period rate of change of period P time 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan

Pulsar Basics cont. . . spin-down luminosity characteristic age magnetic field Assumes magnetic dipole braking in a vacuum 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan
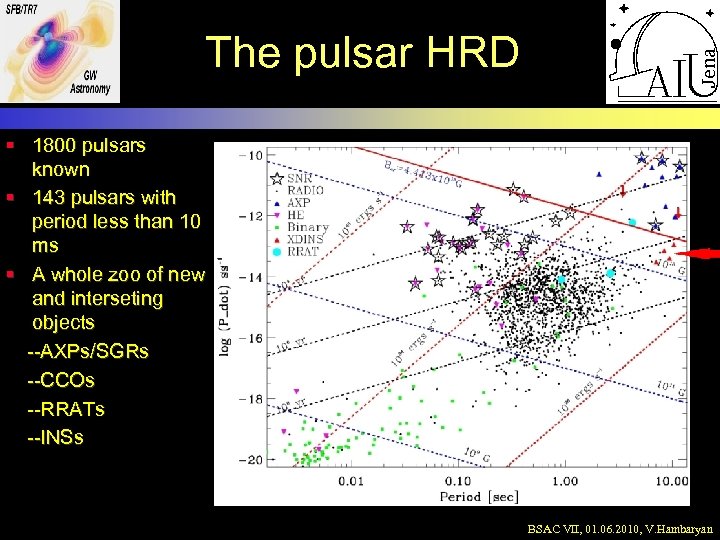
The pulsar HRD § 1800 pulsars known § 143 pulsars with period less than 10 ms § A whole zoo of new and interseting objects --AXPs/SGRs --CCOs --RRATs --INSs binary BSAC VII, 01. 06. 2010, V. Hambaryan

Neutron star mass and radius linking with measurable phenomena Arzoumanian (2009) BSAC VII, 01. 06. 2010, V. Hambaryan
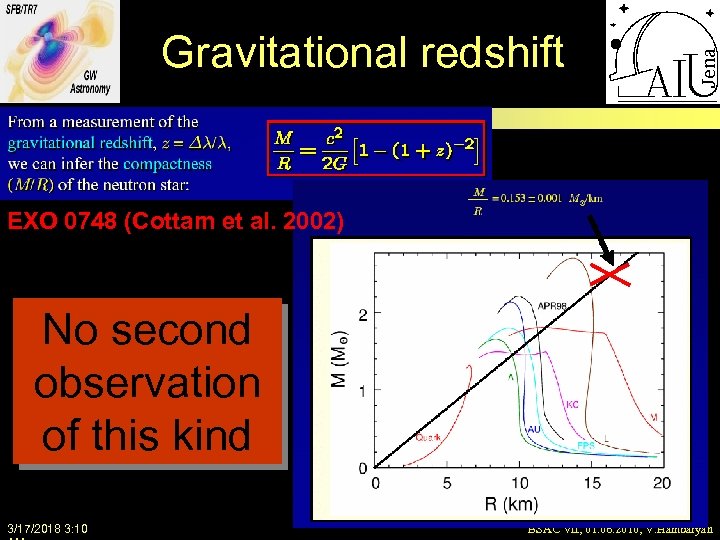
Gravitational redshift EXO 0748 (Cottam et al. 2002) No second observation of this kind 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan
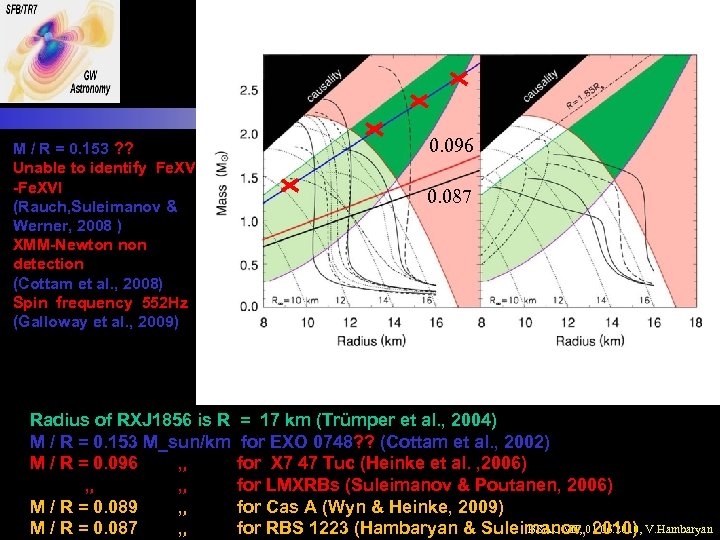
M / R = 0. 153 ? ? Unable to identify Fe. XV -Fe. XVI (Rauch, Suleimanov & Werner, 2008 ) XMM-Newton non detection (Cottam et al. , 2008) Spin frequency 552 Hz (Galloway et al. , 2009) Radius of RXJ 1856 is R M / R = 0. 153 M_sun/km M / R = 0. 096 „ „ „ M / R = 0. 089 „ M / R = 0. 087 „ 0. 096 0. 087 = 17 km (Trümper et al. , 2004) for EXO 0748? ? (Cottam et al. , 2002) for X 7 47 Tuc (Heinke et al. , 2006) for LMXRBs (Suleimanov & Poutanen, 2006) for Cas A (Wyn & Heinke, 2009) BSAC VII, 2010) for RBS 1223 (Hambaryan & Suleimanov, 01. 06. 2010, V. Hambaryan

Method • Bayesian methodology • Bayesian Variability detection • Bayesian Periodicity search 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan

What is a Bayesian approach? • Three-fold task: What the method is? How it works? Why it? 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan

What the method is? • Classical approach or Sampling Statistics Given the data D, how probable is variation in the data, given model M, model parameters q, and any other relevant prior information I ? P(D|q. MI) or P(D|MI) • Bayesian methodology Inverse: How probable are models or model parameters given data? P(q|DMI) or P(M|DI) 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan

What the method is? • Bayesian approch: details Given the data D, how probable are model M, model parameters q? P(q|D, M, I) = P(q|M, I) P(D|q, M, I) | P(D|M, I) P(q|D, M, I) = Posterior probability P(D|q, M, I) = Direct probability P(q|M, I) = Prior probability 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan

How it works? • 1. Specify the hypothesis Carefully specifying the models Mi • 2. Assign direct probailities Assign direct probabilites appropriate to data (Poisson, Bernulii, . . . ) Assign priors for parameters for each Mi • 3. „Turn the crank“ Apply Bayes‘ Theorem to get posterior probability densty distribution Marginalize over uninteresting parameters (some prefer to look at the peak of the posterior without marginalizing) • 4. Report the results For comparing models: it may include, likelihood ratios, probabilities For parameters: one might report the posterior mode, or mean and variance 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan
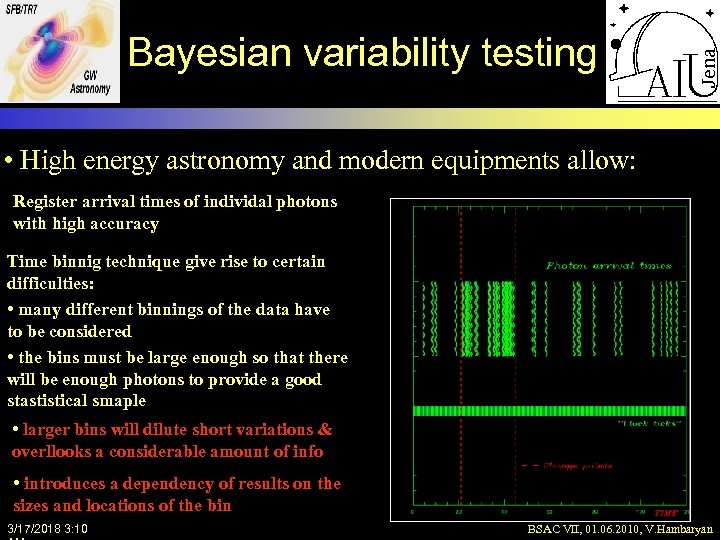
Bayesian variability testing • High energy astronomy and modern equipments allow: Register arrival times of individal photons with high accuracy Time binnig technique give rise to certain difficulties: • many different binnings of the data have to be considered • the bins must be large enough so that there will be enough photons to provide a good stastistical smaple • larger bins will dilute short variations & overllooks a considerable amount of info • introduces a dependency of results on the sizes and locations of the bin 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan
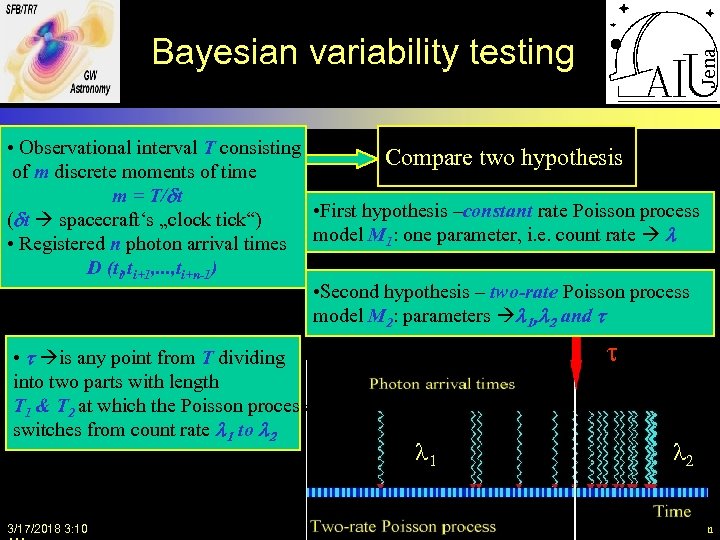
Bayesian variability testing • Observational interval T consisting Compare two hypothesis of m discrete moments of time m = T/dt • First hypothesis –constant rate Poisson process (dt spacecraft‘s „clock tick“) • Registered n photon arrival times model M 1: one parameter, i. e. count rate l D (ti, ti+1, . . . , ti+n-1) • Second hypothesis – two-rate Poisson process model M 2: parameters l 1, l 2 and t • t is any point from T dividing into two parts with length T 1 & T 2 at which the Poisson process switches from count rate l 1 to l 2 3/17/2018 3: 10 t l 1 l 2 BSAC VII, 01. 06. 2010, V. Hambaryan
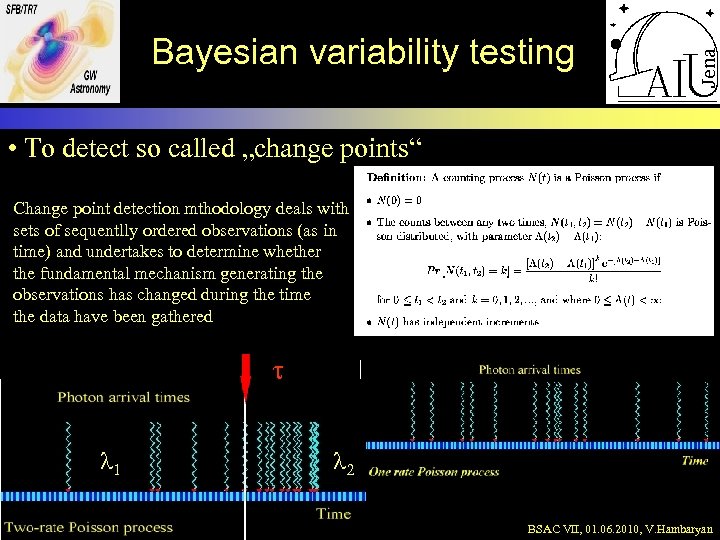
Bayesian variability testing • To detect so called „change points“ Change point detection mthodology deals with sets of sequentlly ordered observations (as in time) and undertakes to determine whether the fundamental mechanism generating the observations has changed during the time the data have been gathered t l 1 3/17/2018 3: 10 l 2 BSAC VII, 01. 06. 2010, V. Hambaryan
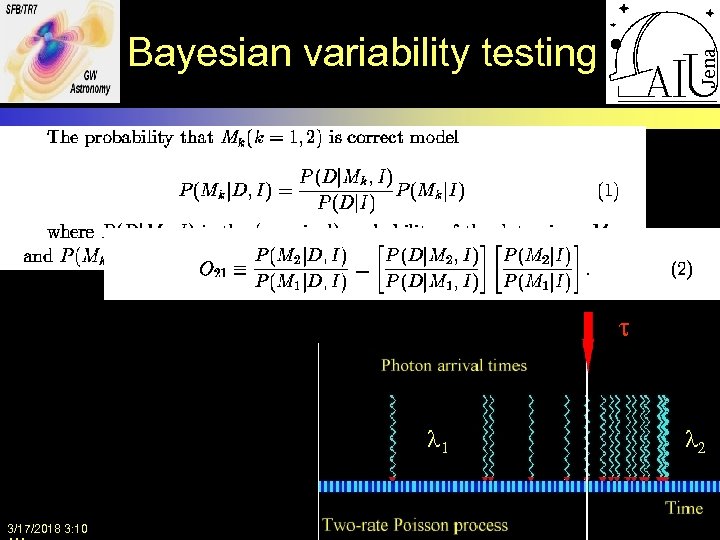
Bayesian variability testing t l 1 3/17/2018 3: 10 l 2 BSAC VII, 01. 06. 2010, V. Hambaryan

Detection of periodicty and QPOs Different methods have been developed for periodicdy search: Leahy et al. , 1983, Ap. J, 272, 256; Scargle, 1989, Ap. J, 343, 874; Swanepoel & De Beer, 1990, Ap. J, 350, 754; Gregory & Loredo (GL), 1992, Ap. J, 398, 146; Bai, 1992, Ap. J, 397, 584; Cincotta et al. , 1995, Ap. J, 449, 231; Cicuttin et al. , 1998, Ap. J, 498, 666 , De Jager 2001. . Simple model of rotating NS • Epoch folding Fi = ti/P – INT(ti/P) • Rayleigh test Z 12 = 2/N [(Scos 2 pfi) 2+(Ssin 2 pfi) 2] BSAC VII, 01. 06. 2010, V. Hambaryan
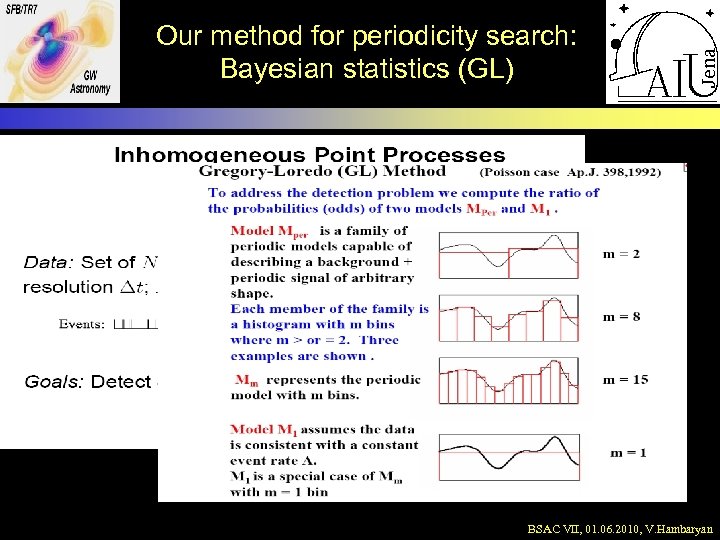
Our method for periodicity search: Bayesian statistics (GL) BSAC VII, 01. 06. 2010, V. Hambaryan
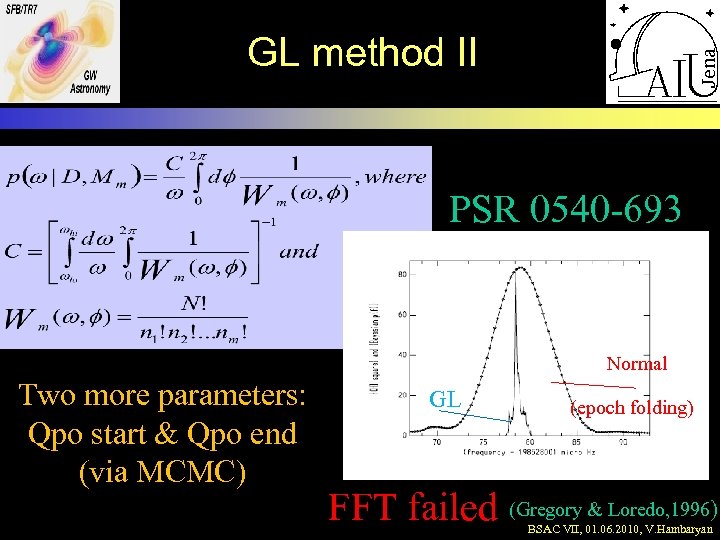
GL method II PSR 0540 -693 Normal Two more parameters: Qpo start & Qpo end (via MCMC) GL (epoch folding) FFT failed (Gregory & Loredo, 1996) BSAC VII, 01. 06. 2010, V. Hambaryan
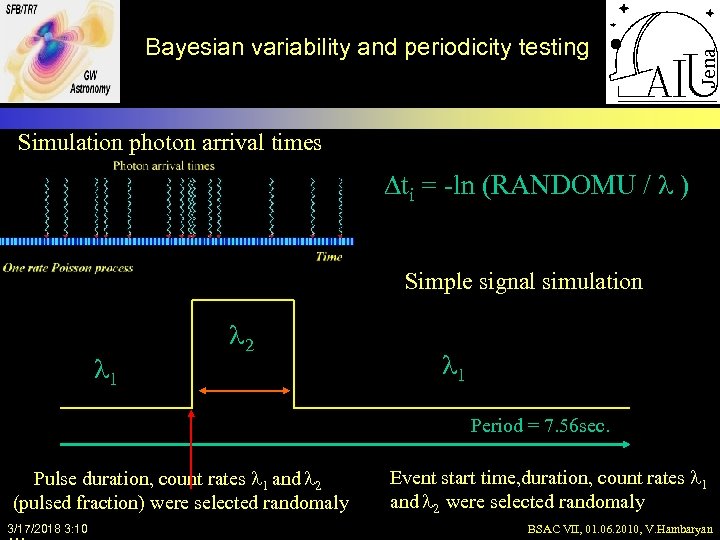
Bayesian variability and periodicity testing Simulation photon arrival times Dti = -ln (RANDOMU / l ) Simple signal simulation l 1 l 2 l 1 Period = 7. 56 sec. Pulse duration, count rates l 1 and l 2 (pulsed fraction) were selected randomaly 3/17/2018 3: 10 Event start time, duration, count rates l 1 and l 2 were selected randomaly BSAC VII, 01. 06. 2010, V. Hambaryan
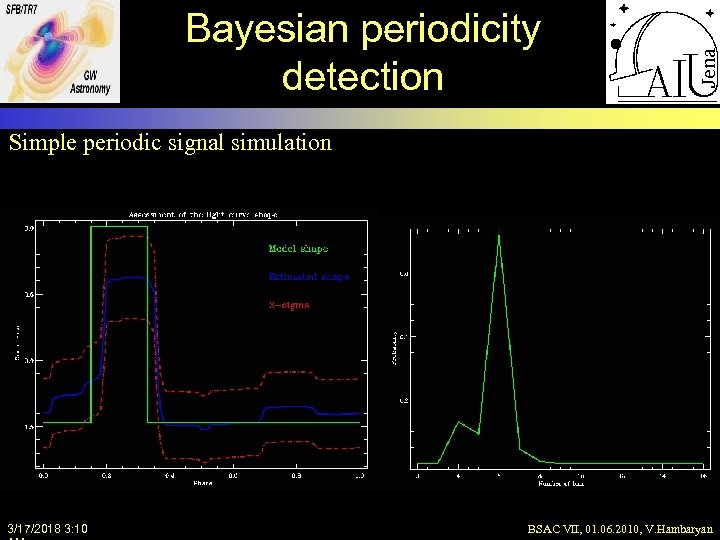
Bayesian periodicity detection Simple periodic signal simulation 3/17/2018 3: 10 BSAC VII, 01. 06. 2010, V. Hambaryan
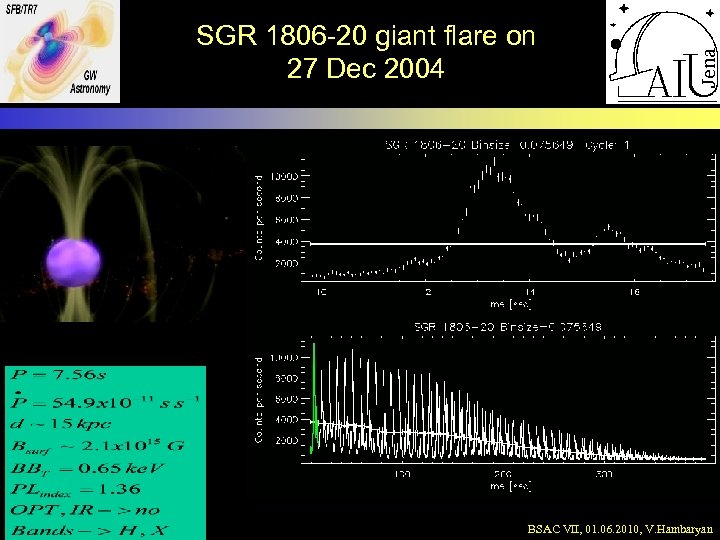
SGR 1806 -20 giant flare on 27 Dec 2004 BSAC VII, 01. 06. 2010, V. Hambaryan
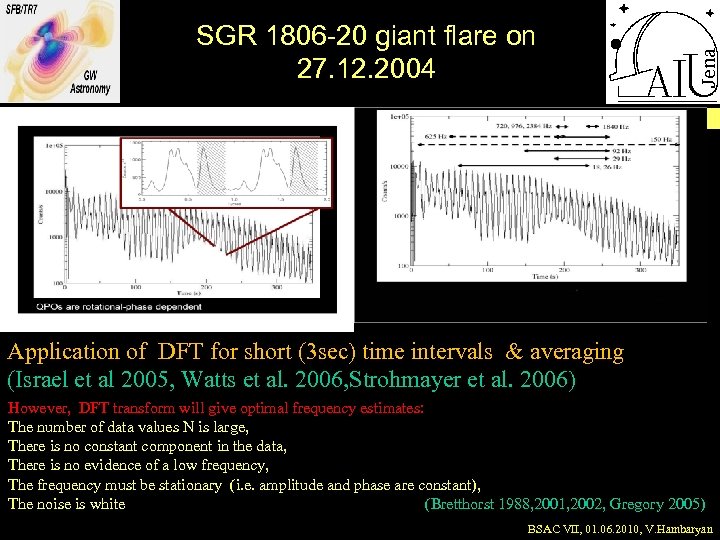
SGR 1806 -20 giant flare on 27. 12. 2004 Application of DFT for short (3 sec) time intervals & averaging (Israel et al 2005, Watts et al. 2006, Strohmayer et al. 2006) However, DFT transform will give optimal frequency estimates: The number of data values N is large, There is no constant component in the data, There is no evidence of a low frequency, The frequency must be stationary (i. e. amplitude and phase are constant), The noise is white (Bretthorst 1988, 2001, 2002, Gregory 2005) BSAC VII, 01. 06. 2010, V. Hambaryan
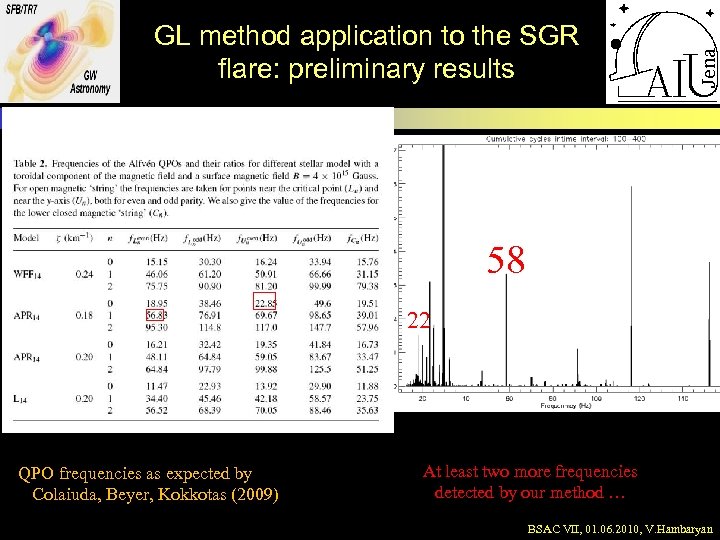
GL method application to the SGR flare: preliminary results 58 22 QPO frequencies as expected by Colaiuda, Beyer, Kokkotas (2009) At least two more frequencies detected by our method … BSAC VII, 01. 06. 2010, V. Hambaryan
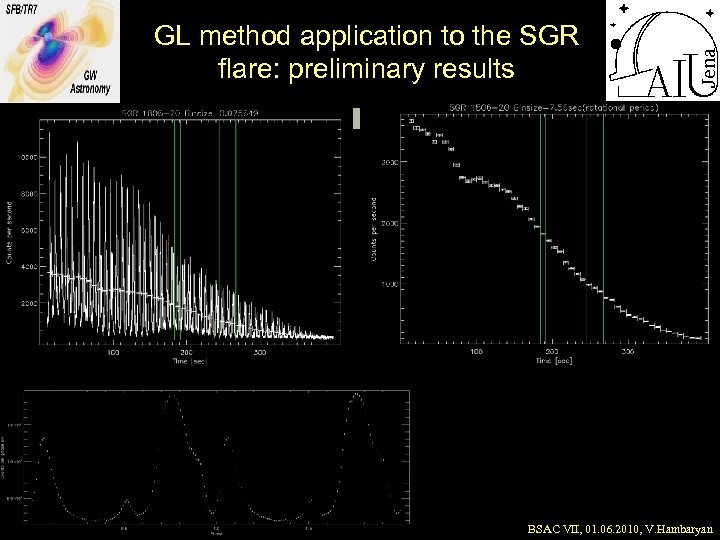
GL method application to the SGR flare: preliminary results BSAC VII, 01. 06. 2010, V. Hambaryan
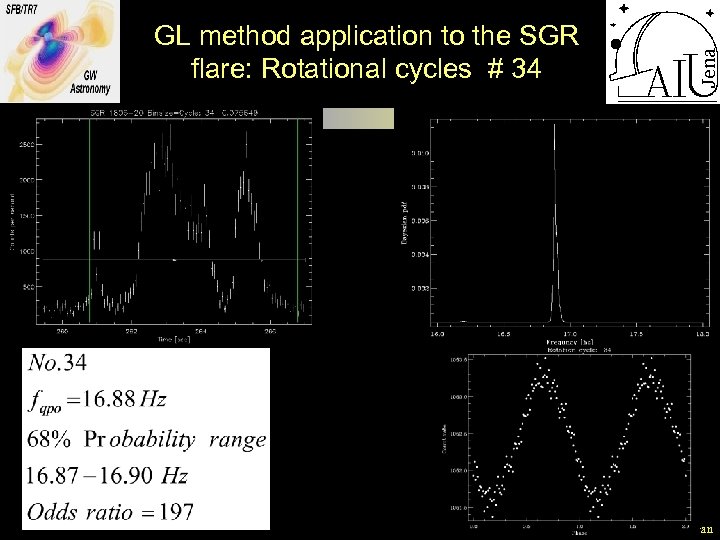
GL method application to the SGR flare: Rotational cycles # 34 BSAC VII, 01. 06. 2010, V. Hambaryan
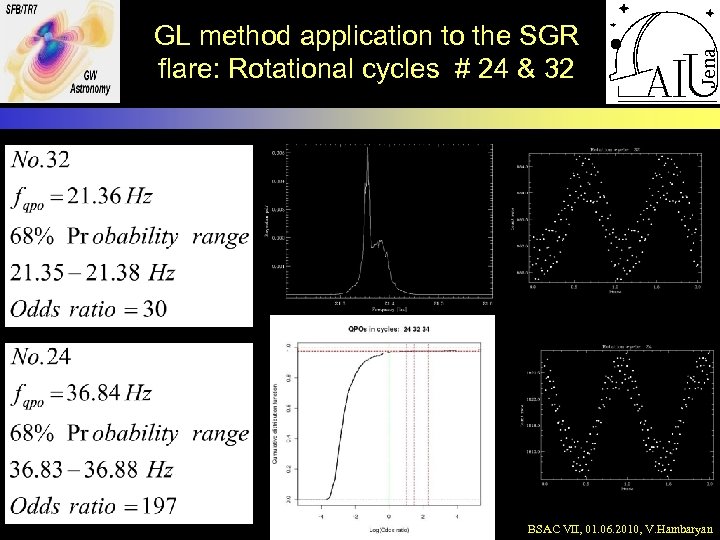
GL method application to the SGR flare: Rotational cycles # 24 & 32 BSAC VII, 01. 06. 2010, V. Hambaryan

Problems & Plans… Smaller flares, smaller vibrations? v. Giant flares are rare and unpredictable events. v. Could the more regular intermediate and normal flares also excite seismic vibrations? v. Analaysis should be performed: Intermediate & normal SGR flares Burst active and quiter periods v Constrain and refine QPO models with frequency detections v Prediction of QPOs also in neutron stars with lower magnetic fields v search for smaller flares, activity phases on neutron stars with lower magnetic fields (AXPs & M 7) v. More complex model is needed for data analysis: modified GL method taking into account rotational light curve as well piecewise constant (apodizing or tempering) flare decay Qpo start & end times will be included as free parameters and derived via MCMC approach BSAC VII, 01. 06. 2010, V. Hambaryan

Conclusions… • To bin or not to bin. . . • To be and not to bin • There are three kinds of lies: • lies • damned lies • and statistics 3/17/2018 3: 11 Mark Twain BSAC VII, 01. 06. 2010, V. Hambaryan
af5d3050bfe83e2ecbda9608d2106dde.ppt