4d6f8bcbcf64b6e7bd458a30baaa0024.ppt
- Количество слайдов: 24

Basic Statistics for Business and Economics Fifth Edition Chapter 13 Linear Regression and Correlation Douglas William Samuel Irwin/Mc. Graw-Hill

Topics • Dependent and independent variables • Coefficient of correlation • Least squares regression

Scatter diagram • Describing the relationship between two variables; There are situations where we have to study a relationship between two variables, this called bivariate data. Examples; - A relationship between stocks and the real state industry - A relationship between selling vehicles and the age of buyer. • Scatter diagram; The graphical technique we use to show the relationship between two variables (at least interval or ratio levels). Figure 1
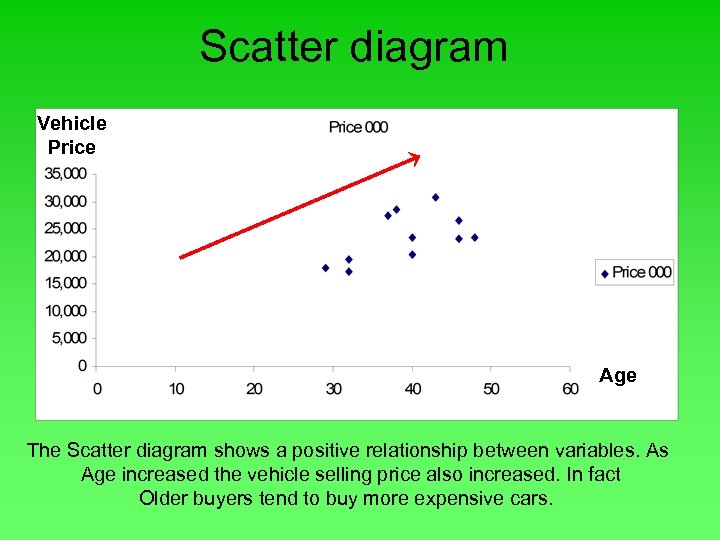
Scatter diagram Vehicle Price Age The Scatter diagram shows a positive relationship between variables. As Age increased the vehicle selling price also increased. In fact Older buyers tend to buy more expensive cars.

Correlation analysis • Correlation analysis is a study of the relationship between variables. The Coefficient of Correlation (r) is a measure of the strength of the relationship between two variables. It can range from -1. 00 to 1. 00. Values of -1. 00 or 1. 00 indicate perfect and strong correlation. Negative values indicate an inverse relationship and positive values indicate a direct relationship. Values close to 0. 0 indicate weak correlation
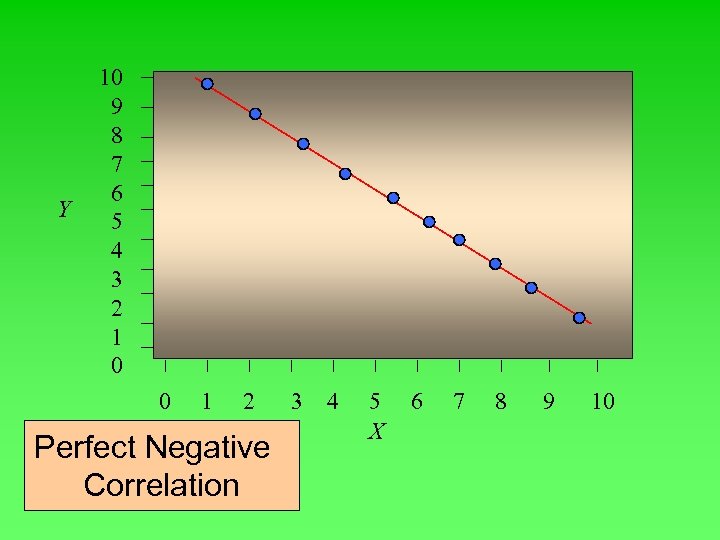
Y 10 9 8 7 6 5 4 3 2 1 0 0 1 2 Perfect Negative Correlation 3 4 5 X 6 7 8 9 10
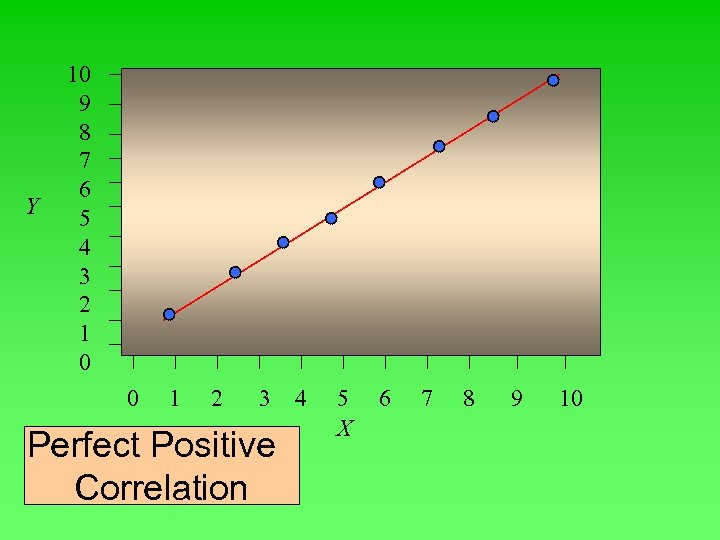
Y 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 Perfect Positive Correlation 4 5 X 6 7 8 9 10
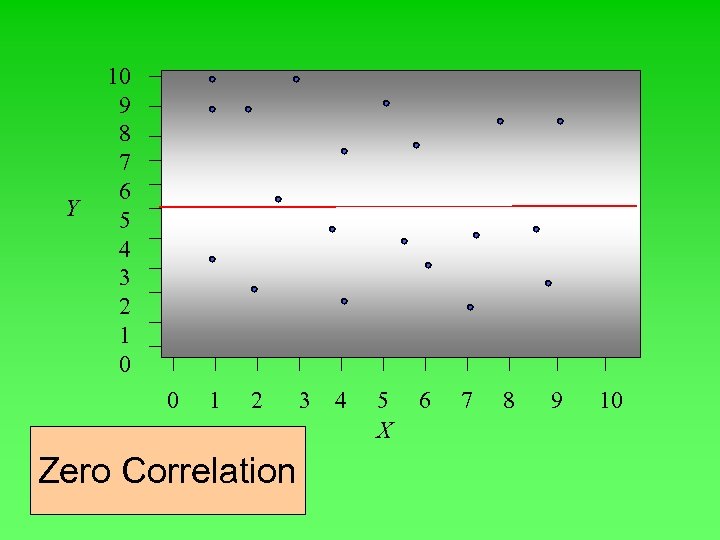
Y 10 9 8 7 6 5 4 3 2 1 0 0 1 2 Zero Correlation 3 4 5 X 6 7 8 9 10
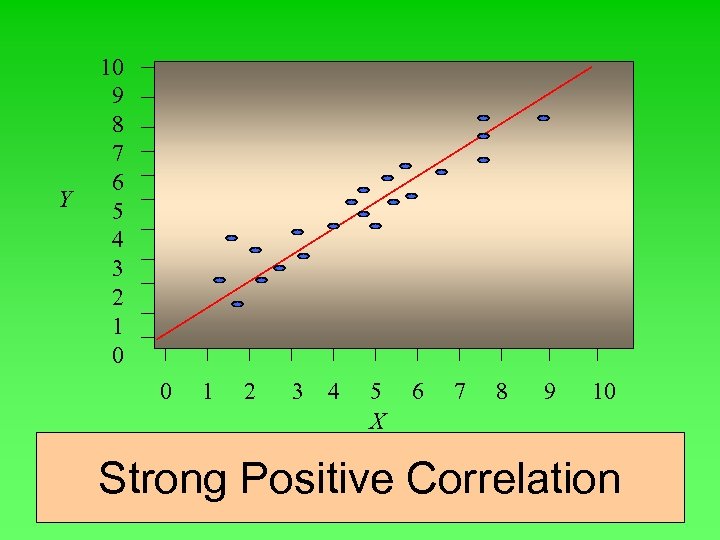
Y 10 9 8 7 6 5 4 3 2 1 0 0 1 2 3 4 5 X 6 7 8 9 10 Strong Positive Correlation

Correlation analysis Example; Suppose the sales manager of Copier Sales of America wants to determine whethere is a relationship between the number of sales calls made in a month and the number of copiers sold that month.
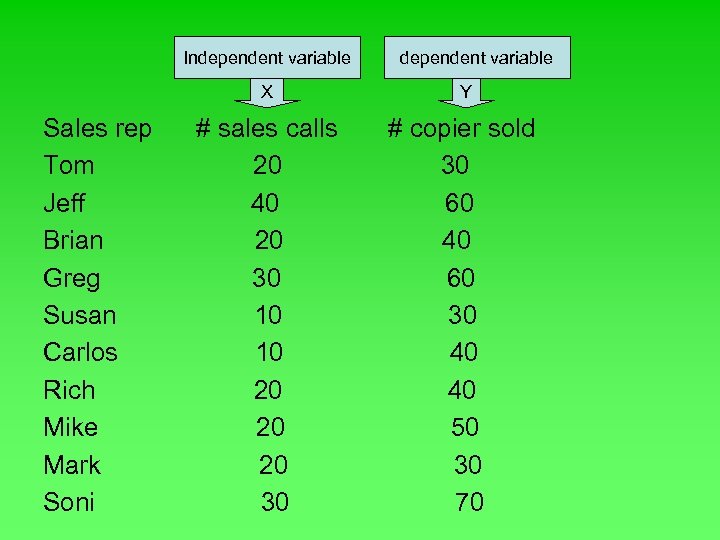
Independent variable X Sales rep Tom Jeff Brian Greg Susan Carlos Rich Mike Mark Soni Y # sales calls 20 40 20 30 10 10 20 20 20 30 # copier sold 30 60 40 60 30 40 40 50 30 70
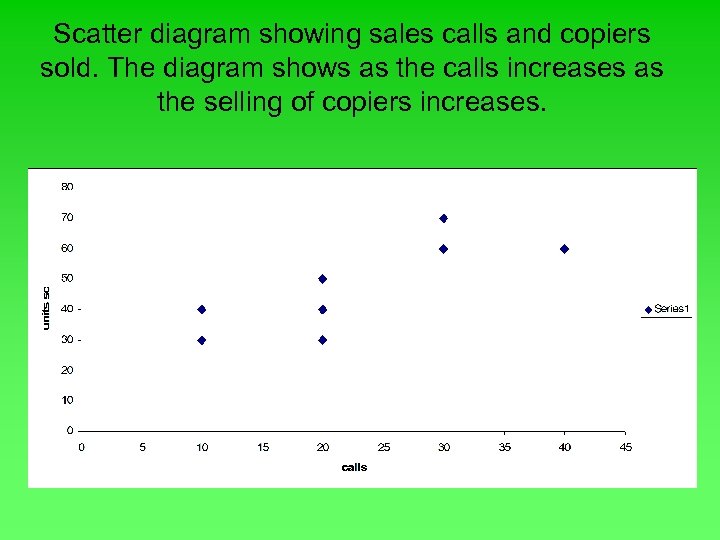
Scatter diagram showing sales calls and copiers sold. The diagram shows as the calls increases as the selling of copiers increases.
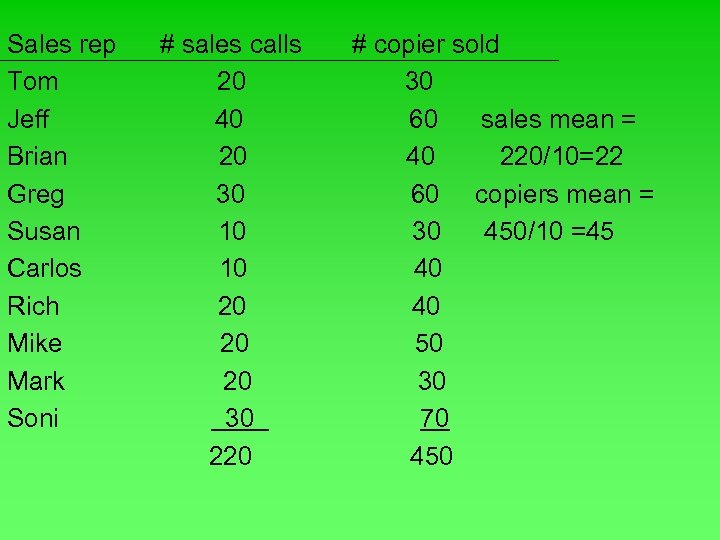
Sales rep Tom Jeff Brian Greg Susan Carlos Rich Mike Mark Soni # sales calls 20 40 20 30 10 10 20 20 20 30 220 # copier sold 30 60 sales mean = 40 220/10=22 60 copiers mean = 30 450/10 =45 40 40 50 30 70 450
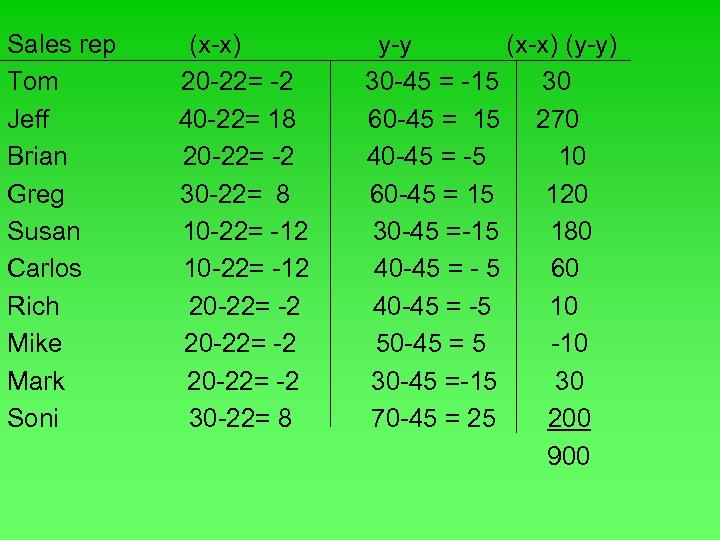
Sales rep Tom Jeff Brian Greg Susan Carlos Rich Mike Mark Soni (x-x) 20 -22= -2 40 -22= 18 20 -22= -2 30 -22= 8 10 -22= -12 20 -22= -2 30 -22= 8 y-y (x-x) (y-y) 30 -45 = -15 30 60 -45 = 15 270 40 -45 = -5 10 60 -45 = 15 120 30 -45 =-15 180 40 -45 = - 5 60 40 -45 = -5 10 50 -45 = 5 -10 30 -45 =-15 30 70 -45 = 25 200 900

Correlation analysis Correlation coefficient r =S(X – X)(Y – Y) (n-1)sxsy Sx is the standard deviation of sales calls= 9. 189 Sy is the standard deviation of copier sold = 14. 337 r= 900 (10 -1)(9. 189(14. 337) r =. 759 The coefficient determination = (r)² = (. 759)² =. 576

Correlation analysis Exercises page 382

Regression analysis Technique used to develop the equation to express the linear ( straight line) relationship between two variables. The equation will estimate the value of the dependent variable (Y) based on the selected value of the independent variable (X). If we take our previous example about the sales people calls, the following scatter diagram represent the judgments of four people;
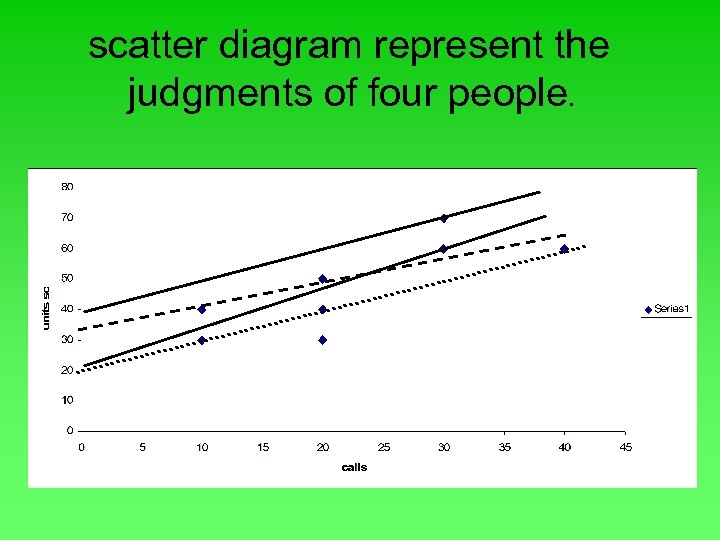
scatter diagram represent the judgments of four people.

Regression analysis Judgment will be eliminated by determining the regression line using a mathematical method called the “ Least squares principle” There are three equation to draw the line; (1) Y΄ = a + b. X Y΄; read, Y prime, is the predicted value of the Y variable for a selected X value. a; is the Y intercept, it’s the estimated of Y when X=0 b; is the Slope of the line. X; is any value of the independent variable that is selected.

Regression analysis (2) b=r Sy Sx r ; is the correlation coefficient Sy; is the standard deviation of Y Sx; is the standard deviation of X

Regression analysis (3) a= Y - b. X Y; is the mean of Y values X; is the mean of X values

Example; recall the example involving Copier Sales of America. What is the expected number of copiers sold by a representative who made 20 calls ? Steps of the solution: (1) b = r Sy Sx b =. 759 ( 14. 337) = 1. 1842 9. 189 (2) a= Y - b. X a = 45 – (1. 1842) 22 = 18. 9476 (3) Y΄ = a + b. X = 18. 9476 + 1. 1842 X X = 20 calls = 42. 6316 copiers to be sold in 20 calls
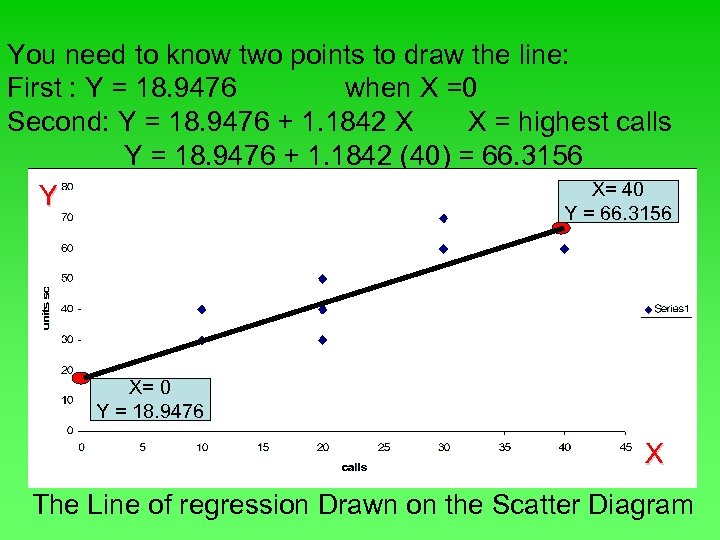
You need to know two points to draw the line: First : Y = 18. 9476 when X =0 Second: Y = 18. 9476 + 1. 1842 X X = highest calls Y = 18. 9476 + 1. 1842 (40) = 66. 3156 X= 40 Y Y = 66. 3156 X= 0 Y = 18. 9476 X The Line of regression Drawn on the Scatter Diagram

Correlation analysis Exercises page 390
4d6f8bcbcf64b6e7bd458a30baaa0024.ppt