a34ec1304dd89b9249b4730b85e190a7.ppt
- Количество слайдов: 70

Basic OWL Restrictions n An owl: Restriction is an owl: Class defined by describing conditions on the individuals it contains n This is the basis for extension of models q q q If we can describe a set of individuals in terms of known classes, we can use that description to define a new class The new class in turn can be used to describe individuals in a yet newer class And so on
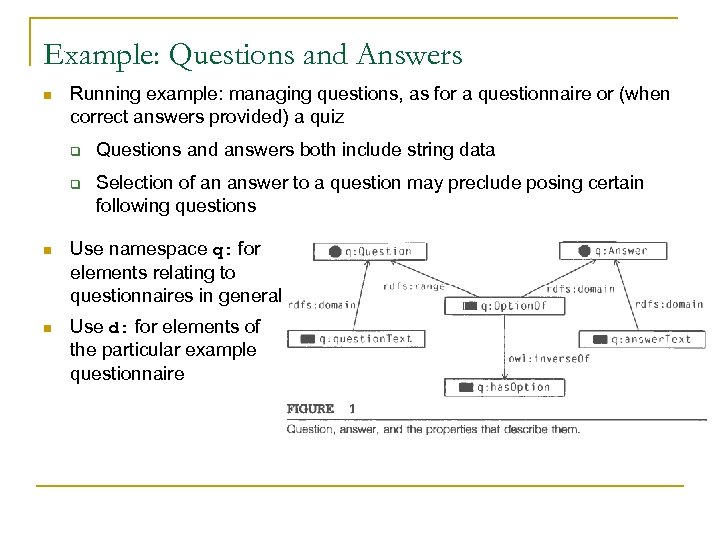
Example: Questions and Answers n Running example: managing questions, as for a questionnaire or (when correct answers provided) a quiz q q Questions and answers both include string data Selection of an answer to a question may preclude posing certain following questions n Use namespace q: for elements relating to questionnaires in general n Use d: for elements of the particular example questionnaire

n The basic schema for the questionnaire @prefix rdf: <http: //www. w 3. org/1999/02/22 -rdf-syntax-ns#>. xsd: <http: //www. w 3. org/2001/XMLSchema#>. rdfs: <http: //www. w 3. org/2000/01/rdf-schema#>. owl: <http: //www. w 3. org/2002/07/owl#>. @prefix q: <http: //www. aboutq. org/vocabulary#>. q: Answer a owl: Class. q: Question a owl: Class. q: option. Of a owl: Object. Property; rdfs: domain q: Answer; rdfs: range q: Question; owl: inverse. Of q: has. Option a owl: Object. Property. q: answer. Text a owl: Datatype. Property; rdfs: domain q: Answer; rdfs: range xsd: string. q: question. Text a owl: Functional. Property, owl: Datatype. Property; rdfs: domain q: Question; rdfs: range xsd: string.
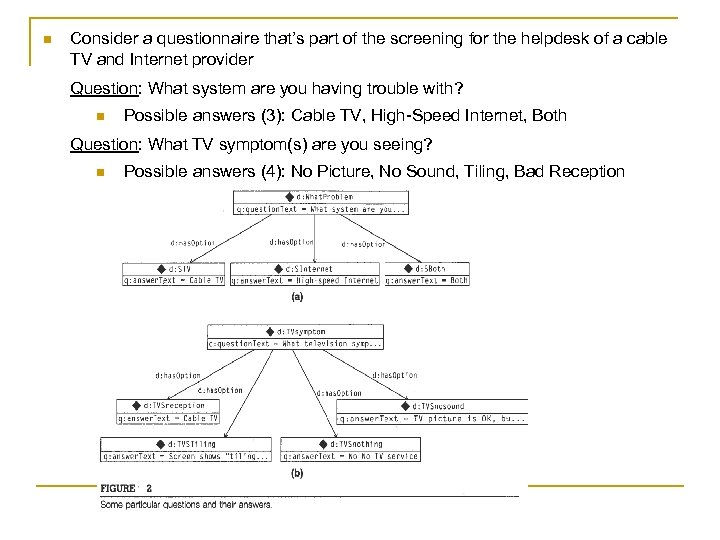
n Consider a questionnaire that’s part of the screening for the helpdesk of a cable TV and Internet provider Question: What system are you having trouble with? n Possible answers (3): Cable TV, High-Speed Internet, Both Question: What TV symptom(s) are you seeing? n Possible answers (4): No Picture, No Sound, Tiling, Bad Reception

@prefix d: <http: //www. fredservice. org/helpdesk#>. d: What. Problem a q: Question; q: has. Option d: STV, d: SInternet, d: SBoth; q: question. Text "What system are you having trouble with? ". d: STV a q: Answer; q: answer. Text "Cable TV". d: SInternet a q: Answer; q: answer. Text "High-speed Internet". d: SBoth a q: Answer; q: answer. Text "Both". d: TVsymptom a q: Question; q: question. Text "What TV symptoms are you having? "; q: has. Option d: TVSnothing, d: TVSnosound, d: TVStiling, d: TVSreception. d: TVSnothing a q: Answer; q: answer. Text "No Picture". d: TVSnosound a q: Answer ; q: answer. Text "No Sound". d: TVStiling a q: Answer; q: answer. Text "Tiling".

n Consider how we’d record answers to the questions n Define subproperty q: has. Selected. Option of q: has. Option q: has. Selected. Option a owl: Object. Property; rdfs: sub. Property. Of q: has. Option. n When the user answers a question, a triple is entered to indicate the option selected q E. g. , if the user selects “Cable TV” for question d: What. Problem, we add to the store d: What. Problem q: has. Selected. Option d: STV. q No need to remove any triple from the store n The original q: has. Option relationship between d: what. Problem and d: STV still holds

Adding Restrictions n The OWL construct for creating class descriptions based on descriptions of prospective class members is owl: Restriction q q A subclass of owl: Class Defined by a description of its members in terms of existing properties and classes n The class of all things, owl: Thing is unrestricted—see the AAA slogan n Define a owl: Restriction with a description restricting the kinds of things that can be said about class members n E. g. , given property : orbits. Around, can say anything : orbits. Around anything else q Restricting the value of : orbits. Around by saying its object must be : The. Sun defines the class of all things orbiting around the sun

n Three of the restrictions are owl: all. Values. From, owl: some. Values. From, owl: has. Value n Keyword owl: on. Property specifies the property used in the definition of the restriction class q E. g. , for the restriction defining the objects orbiting around the sun, use owl: on. Property orbits. Around n Membership in a restriction class must satisfy the conditions given by the kind of restriction and the owl: on. Property specification

owl: some. Values. From n n owl: some. Values. From produces a restriction of the form “All individuals for which at least 1 value of property P comes from class C” E. g. , define a class for all-star players as “All individuals for which at least 1 value of property : plays. For comes from class : All. Star. Team” [ a owl: Restriction; owl: on. Property : plays. For; owl: some. Values. From : All. Star. Team] q The subject of all 3 triples here is a bnode—something is a restriction class defined on property : plays. For requiring … n q There’s no name for the restriction class (yet)—it’s an “unnamed class” If an individual actually has some value from class : All. Star. Team for property : plays. For, then it’s in this restriction class

Example: Answered Questions n Recall q q property q: has. Option (relating a question to an answer option) and its subproperty q: has. Selected. Option (those answers selected) n Now address the problem of selecting which question to ask n Usually don’t ask a question for which we already have an answer q An answered question is one with some value from class q: Answer for property q: has. Selected. Option q: Anwered. Question owl: equivalent. Class [ a owl: Restriction; owl: on. Property q: has. Selected. Option; owl: some. Value. From q: Anwer].

n Given the asserted triples d: What. Problem q: has. Selected. Option d: STV a Answer. individual d: What. Problem satisfies the conditions of the restriction class so is a member of class q: Answered. Question n The inference is: Given d: What. Problem a [ a owl: Restriction; owl: on. Property q: has. Seelcted. Option; owl: some. Value. From q: Anwer]. q by the semantics of owl: equivalent. Class infer d: What. Problem a Answered. Question
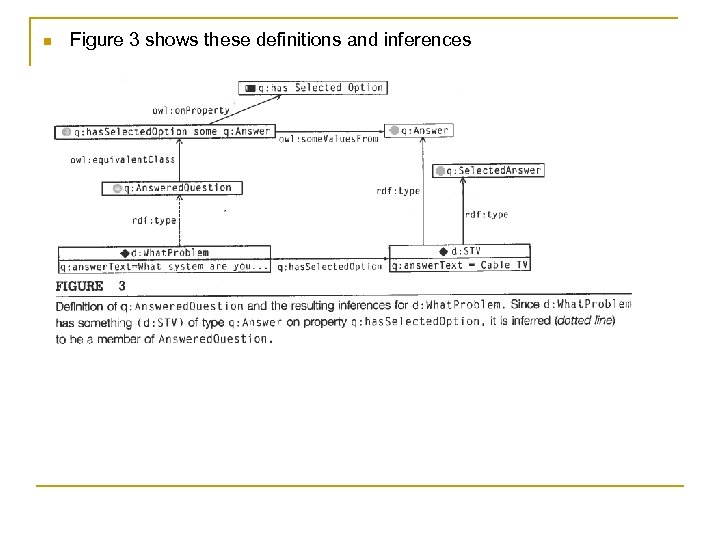
n Figure 3 shows these definitions and inferences

owl: all. Values. From n owl: all. Values. From produces a restriction class of the form “the individuals for which all values of property P come from class C” [ a owl: Restriction; owl: on. Property P; owl: all. Values. From C] q If individual x is a member of this restriction, then every value of property P for x is inferred to be in class C

n E. g. , suppose : my. Favorite. All. Star. Team (a member of class : Baseball. Team) is a member of [ a owl: Restriction; owl: on. Property : has. Player; owl: all. Values. From : Star. Player] q n Then every player on : My. Favorite. All. Star. Team is a : Star. Player E. g. , suppose further that we have the triples : My. Favorite. All. Star. Team : has. Player : Gonzales. : My. Favorite. All. Star. Team : has. Player : Kaneda. q Then both : Kaneda and : Gonzales are of type : Star. Player

n owl: some. Value. From is defined as a restriction class such that there’s at least 1 member of a class with a given property q n So it implies there is such a member owl: all. Values. From technically means “if there any members of the class, then they all must have the property” q This doesn’t imply that there any members

Example: Question Dependencies n For our questionnaire, we ask certain questions only after particular answers are given n First define the class of all selected answers based on the q: has. Selected. Option property n Define a class for the selected answers and ensure that any option that’s been selected appears in the class q: Selected. Answer a owl: Class; rdfs: sub. Class. Of q: Answer. q: has. Selected. Option rdfs: range q: Selected. Answer. n Introduce class q: Enabled. Question of questions that can be asked (after selected answers have been given) q: Enabled. Question a owl: Class.

n An answer enables a question (property q: enables. Candidate) if selecting that answer causes the system to consider that question as a candidate for the next question asked q: enables. Candidate a owl: Object. Property; rdfs: domain q: Answer; rdfs: range q: Question. n E. g. , ask a question about TV problems only if the answer to the 1 st question indicates such a problem d: STV q: enables. Candidate d: TVsymptom. d: SBoth q: enables. Candidate d: TVsymptom.

n An answer in the following restriction class has all the questions it enables enabled [ a owl: Restriction; owl: on. Property q: enables. Candidate; owl: all. Values. From q: Enabled. Question] n Any member of q: Selected. Answer should also be a member of this restriction class q: Selected. Answer rdfs: sub. Class. Of [ a owl: Restriction; owl: on. Property q: enables. Candidate; owl: all. Values. From q: Enabled. Question]

Follow out an example n When the user selects answer “Cable TV” for the first question, we assert d: STV a q: Slected. Answer. n Because of the subclass relation, d: STV is also in the restriction class d: STV a [ a owl: Restriction; owl: on. Property q: enables. Candidate; owl: all. Values. From q: Enabled. Question] n For any answer x that’s a member of this restriction, any question related to x by q: enables. Candidate must be a member of q: Enabled. Question n Since d: STV q: enables. Candidate d: TVsymptom. we infer d: TVsymptom a q: Enabled. Question. n Note that we also have d: SBoth q: enables. Candidate d: TVsymptom.
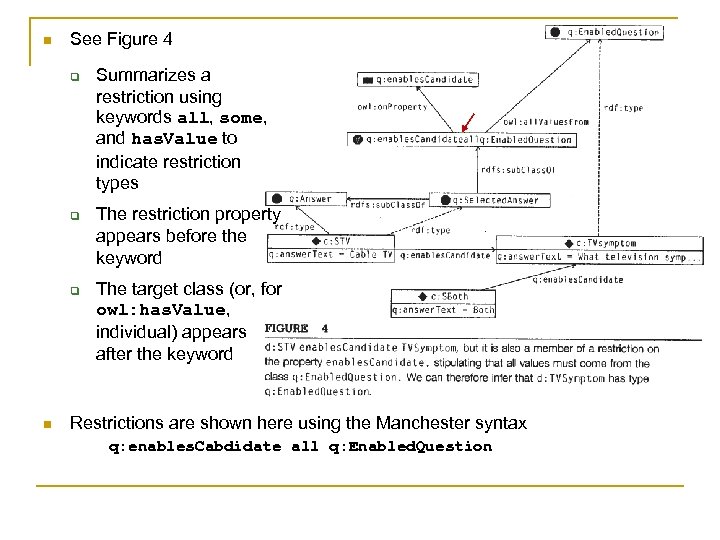
n See Figure 4 q q q n Summarizes a restriction using keywords all, some, and has. Value to indicate restriction types The restriction property appears before the keyword The target class (or, for owl: has. Value, individual) appears after the keyword Restrictions are shown here using the Manchester syntax q: enables. Cabdidate all q: Enabled. Question
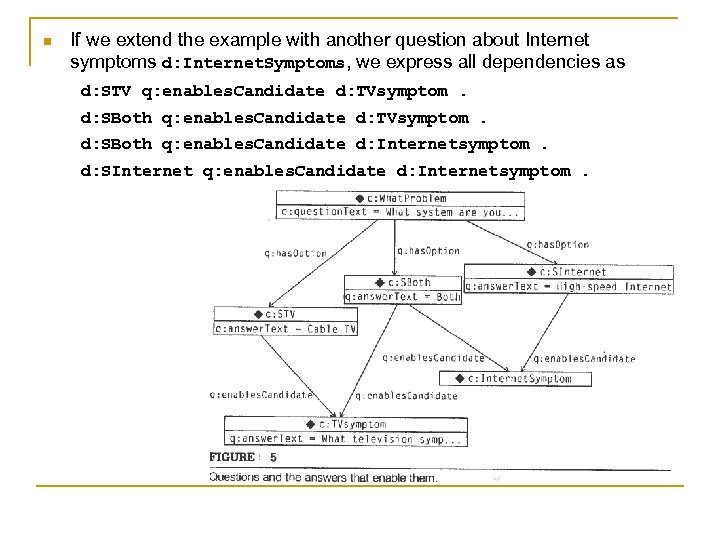
n If we extend the example with another question about Internet symptoms d: Internet. Symptoms, we express all dependencies as d: STV q: enables. Candidate d: TVsymptom. d: SBoth q: enables. Candidate d: Internetsymptom. d: SInternet q: enables. Candidate d: Internetsymptom.

Example: Prerequisites n We’ve supposed that answering one question makes all dependent questions eligible n Questions are also related as prerequisites q n All a question’s prerequisites must be answered appropriately for it to be eligible Triples defining part of a questionnaire d: Neighbors. Too a q: Question; q: has. Option d: NTY, d: NTN, d: NTDK; q: Question. Text "Are other customers in your building also experiencing problems? ". d: NTY a q: Answer; q: answer. Text "Yes, my neighbors are experiencing the same problem. ". d: NTN a q: Answer; q: answer. Text "No, my neighbors are not experiencing the same problem. ". d: NTDK a q: Answer; q: answer. Text "I don’t know. ".
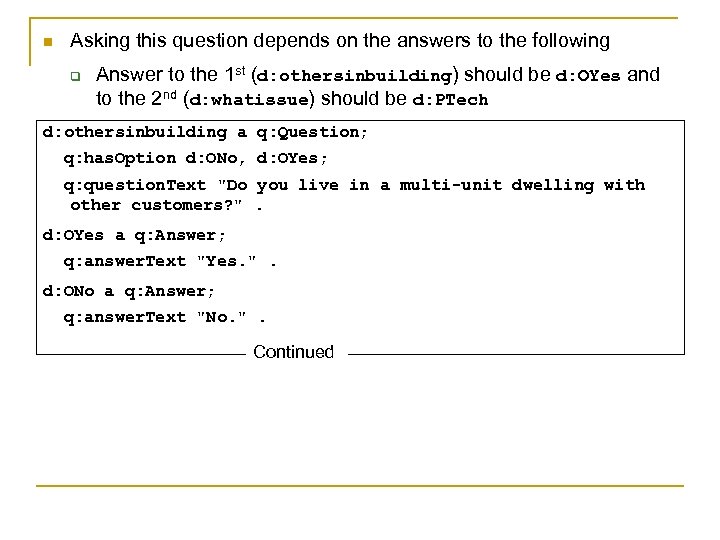
n Asking this question depends on the answers to the following q Answer to the 1 st (d: othersinbuilding) should be d: OYes and to the 2 nd (d: whatissue) should be d: PTech d: othersinbuilding a q: Question; q: has. Option d: ONo, d: OYes; q: question. Text "Do you live in a multi-unit dwelling with other customers? ". d: OYes a q: Answer; q: answer. Text "Yes. ". d: ONo a q: Answer; q: answer. Text "No. ". Continued
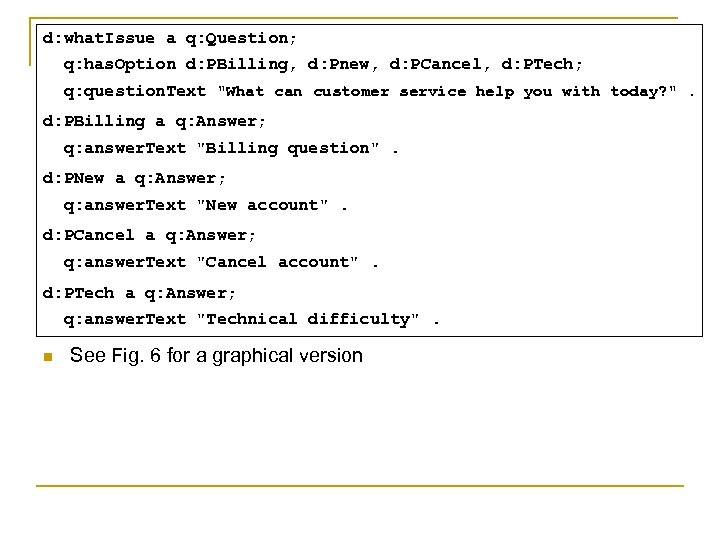
d: what. Issue a q: Question; q: has. Option d: PBilling, d: Pnew, d: PCancel, d: PTech; q: question. Text "What can customer service help you with today? ". d: PBilling a q: Answer; q: answer. Text "Billing question". d: PNew a q: Answer; q: answer. Text "New account". d: PCancel a q: Answer; q: answer. Text "Cancel account". d: PTech a q: Answer; q: answer. Text "Technical difficulty". n See Fig. 6 for a graphical version
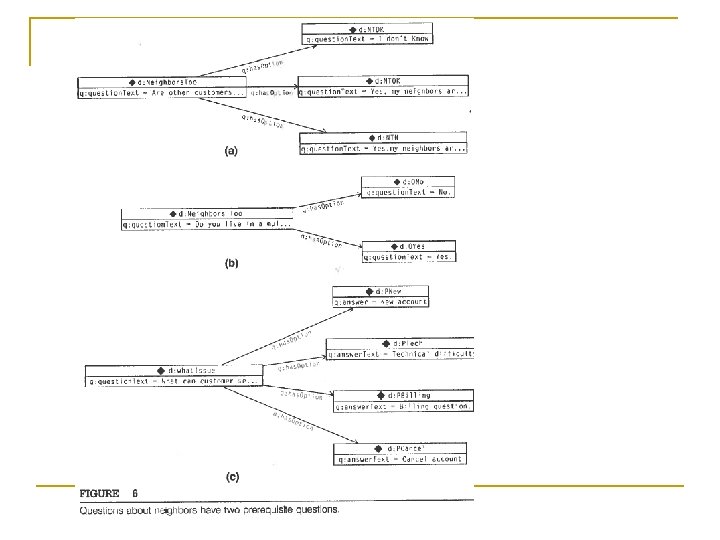

Challenge 22 n Model the relationship between d: Neighbors. Too, d: what. Issue, d: othersinbuilding So we ask d: Neighbors. Too only when we have appropriate answers to the other 2 n Introduce a property to relate a question to its prerequisites q: has. Prerequisite a rdf: Property; rdfs: domain q: Question; rdfs: range q: Answer. n Indicate the relationship between questions using this d: Neighbors. Too q: has. Prerequisite d: PTech, d: OYes. n See Figure 7
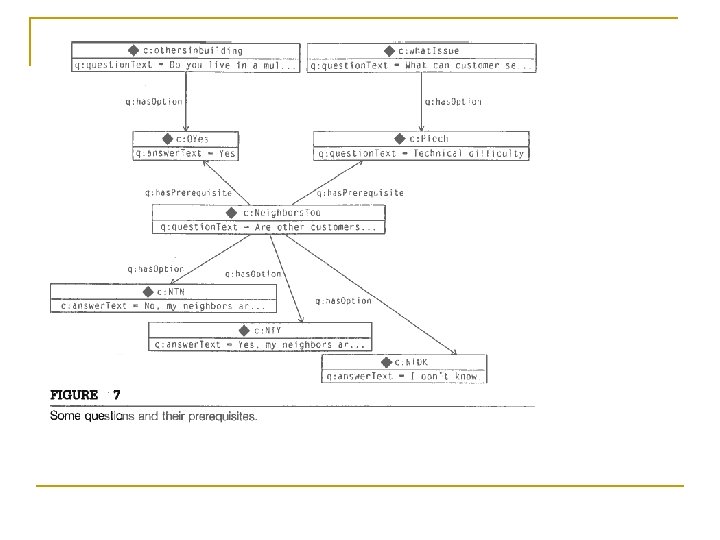

n Now say that we infer something is a d: Enabled. Question if all its prerequisite answers are selected n First assert [ a owl: Restriction; owl: on. Property q: has. Prerequisite; owl: all. Values. From q: Selected. Answer] rdfs: sub. Class. Of q: Enabled. Question. n For individual x to satisfy this restriction, every time there’s a triple x q: has. Prerequisite y. y must be a member of d: Selected. Answer

n But, by the Open World Assumption, we don’t know whethere’s another triple of this form where y isn’t in d: Selected. Answer n The rest of this challenge must wait until we discuss the ways we can (partially) close the world in OWL q Basic idea: If we can say how many prereqs a question has, then we’ll know when all have been selected

owl: has. Value n The 3 rd kind of restriction is owl: has. Value n Produces a restriction of the form “All individuals having value A for property P” [ a owl: Restriction; owl: on. Property P; owl: has. Value A ] n A special case of the owl: some. Values. From restriction where class C is singleton set {A } q n Distinguished since it’s a common and useful modeling form Turns a description of a specific instance into a class description q E. g. , can define n “The set of all planets orbiting the sun” n “The set of all baseball teams in Japan”

Example: Priority Questions n We assign priority levels to our questions n First define a class of priority levels and the individual levels q: Priority. Level a owl: Class. q: High a q: Prioirty. Level. q: Medium a q: Prioirty. Level. q: Low a q: Prioirty. Level. n Then define a property for the priority level (e. g. , of a question) q: has. Priority a rdf: Property; rdfs: range q: Priority. Level. q Don’t give a domain—things other than questions have priorities
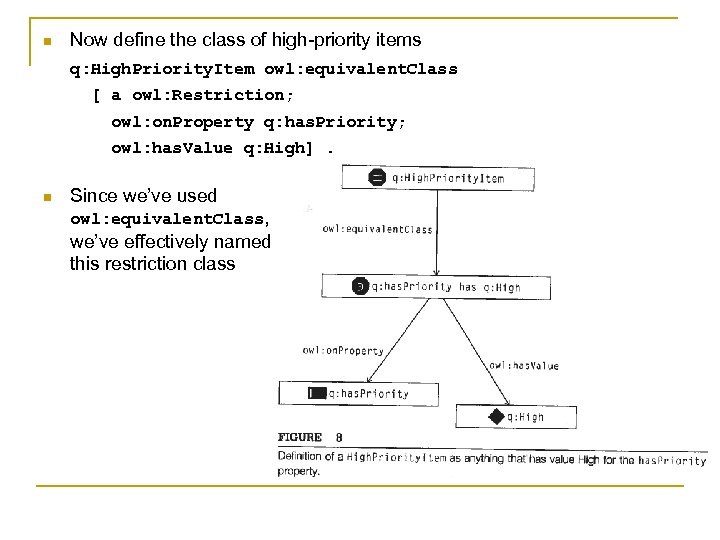
n Now define the class of high-priority items q: High. Priority. Item owl: equivalent. Class [ a owl: Restriction; owl: on. Property q: has. Priority; owl: has. Value q: High]. n Since we’ve used owl: equivalent. Class, we’ve effectively named this restriction class

n Do the same with medium and low priority classes q: Medium. Priority. Item owl: equivalent. Class [ a owl: Restriction; owl: on. Property q: has. Priority; owl: has. Value q: Medium]. q: Low. Priority. Item owl: equivalent. Class [ a owl: Restriction; owl: on. Property q: has. Priority; owl: has. Value q: Low].

n Suppose we assert the priority levels of some questions d: What. Problem q: has. Pritority q: High. d: Internet. Symptom q: has. Priority q: Low. Can infer d: what. Problem a q: High. Priority. Item. d: Internet. Symptom a q: Low. Priority. Item. n Can draw inferences in the other direction too q E. g. , suppose we assert d: TVsymptom a q: High. Priority. Item. q By the semantics of owl: equivalent. Class, infer that d: TVsymptom is a member of the restriction class and bound by its stipulations n So infer d: TVsymptom q: has. Priority q: High.

Challenge Problems Challenge: Local Restriction of Ranges n Saw rdfs: domain and rdfs: range to classify data according to use n In more elaborate modeling situations, finer granularity of domain and range inferences are needed n E. g. , describing a vegetarian diet : Person a owl: Class. : Food a owl: Class. : eats rdfs: domain : Person. : eats rdfs: range : Food. n Instance data : Maverick : eats : Steak.

n From this schema and instance, infer : Maverick a : Person. : Steak a : Food. n Define a variety of diets in more detail n E. g. , a kind of person, : Vegetarian, who eats a particular kind of food, : Vegetarian food : Vegetarian a owl: Class; rdfs: sub. Class. Of : Person. : Vegetarian. Food a owl: Class; rdfs: sub. Class. Of : Food.

n Suppose also : Jen a : Vegetarian; : eats : Marzipan. n We’d like to be able to infer : Marzipan a : Vegetarian. Food. but not make the corresponding inference for Maverick’s steak

Challenge 23 n If we assert : eats rdfs: domain : Vegetarian. : eats rdfs: range : Vegetarian. Food. could make the unwanted inferences to : Maverick a : Vegetarian. : Steak a : Vegetarian. Food. n Correctly model the relationship between vegetarians and vegetarian food

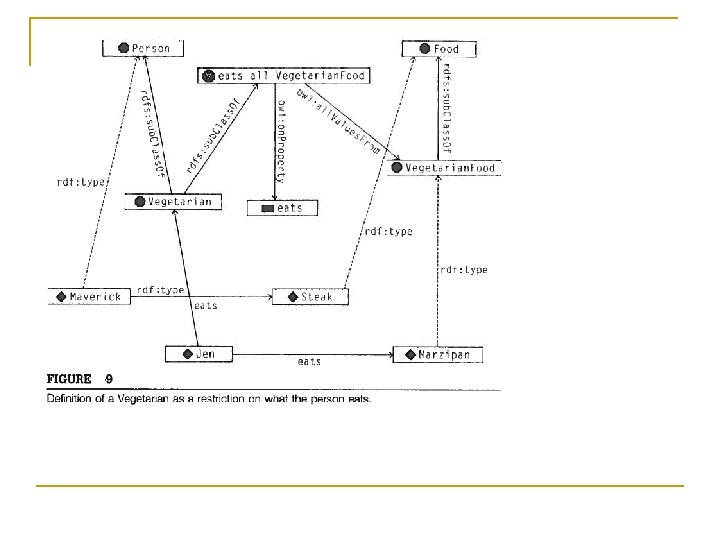
Solution n Define the set of things that eat only : Vegetarian. Food using a owl: all. Values. From restriction q Then assert, using owl: sub. Class. Of, that any : Vegetarian satisfies this condition : Vegetarian rdfs: sub. Class. Of [ a owl: Restriction; owl: on. Property : eats; owl: all. Values. From : Vegetarian. Food].

n Then, since : Jen a : Vegetarian. infer : Jen a [ a owl: Restriction; owl: on. Property : eats; owl: all. Values. From : Vegetarian. Food]. n Combined with : Jen : eats : Marzipan. infer : Marzipan a : Vegetarian. Food. n There’s no stated relationship between : Maverick and : Vegetarian q n Nothing on which to base an inference See Figure 9
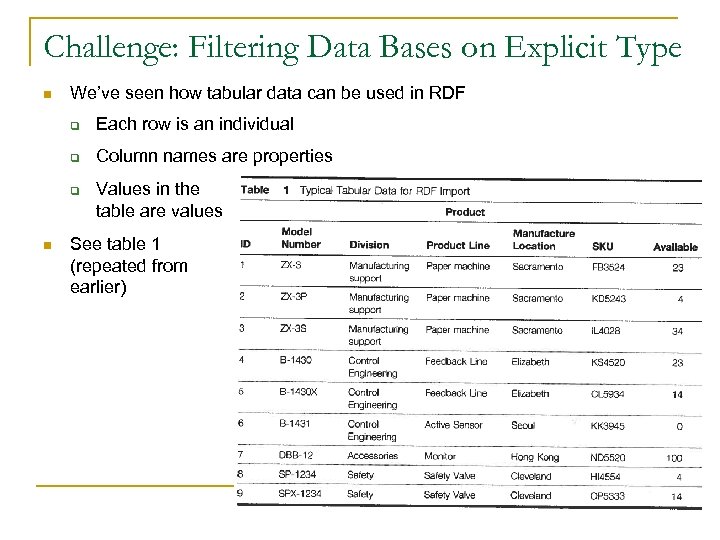
Challenge: Filtering Data Bases on Explicit Type n We’ve seen how tabular data can be used in RDF q Each row is an individual q Column names are properties q n Values in the table are values See table 1 (repeated from earlier)
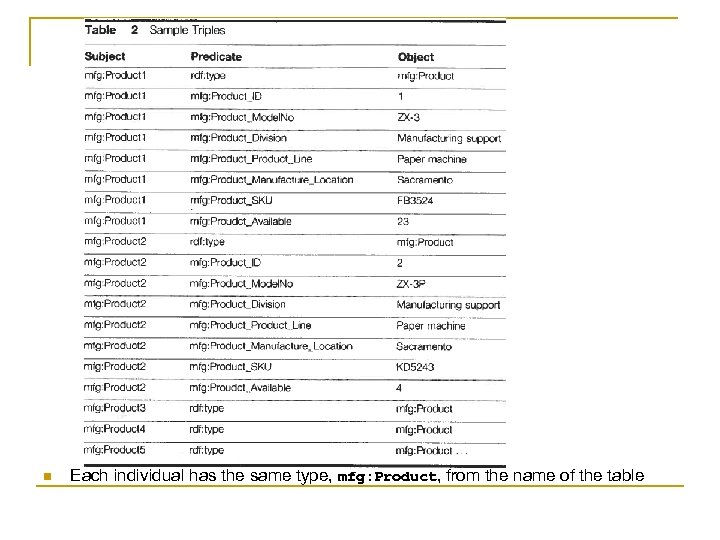
n Each individual has the same type, mfg: Product, from the name of the table

n Limited number of possible values, known in advance, for “Product Line” field: “Paper machine”, “Feedback line”, “Safety valve”, etc. n A more elaborate way to import this info is to q still have one individual per table row but q have rows with different types depending on value of Product Line column q E. g. , mfg: Product 1 rdf: type ns: Paper_machine. mfg: Product 1 rdf: type ns: Feedback_line. mfg: Product 1 rdf: type ns: Monitor. mfg: Product 1 rdf: type ns: Safety. Value. n With a single method for importing tables, all rows become individuals of the same type n A software intensive solution is to write a more elaborate import mechanism q n Lets a user specify which column specifies the type A model-based solution uses an OWL model and an inference engine

Challenge 24 n Build an OWL model letting us infer type info from each individual, based on the value in the “Product Line” field q Use just the simple imported triples seen earlier Solution n The classes for the rows are already known ns: Paper_Machine rdf: type owl: Class. ns: Feedback_Line rdf: type owl: Class. ns: Active_Sensor rdf: type owl: Class. ns: Monitor rdf: type owl: Class. ns: Safety_Valve rdf: type owl: Class.

n Now the class constructors ns: Paper_Machine owl: equivalent. Class [ a owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Paper machine"]. ns: Feedback_Line owl: equivalent. Class [ a owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Feedback line"]. ns: Active_Sensor owl: equivalent. Class [ a owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Active sensor"].

ns: Monitor owl: equivalent. Class [ a owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Monitor"]. ns: Safety_Valve owl: equivalent. Class [ a owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Safety_Valve"].

n For inferences, consider mfg: Product 1 (“ZX-3”) n The following triple has been imported from the table mfg: Product 1 mfg: Product_Line "Paper machine". n So mfg: Product 1 satisfies the condition on the restriction for Paper_Machine, so can infer mfg: Product 1 rdf: type [ owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Paper machine"]. n By the semantics for owl: equivalent. Class, infer mfg: Product 1 rdf: type mns: Paper_Machine.

n And the definition maintains coherence of the date even from new source n E. g. , suppose a new product is defined with os: Product. A a mfg: Paper_Machine. n The semantics of owl: euivalent. Class means that all members of mfg: Paper_Machine are also members of the restriction, so os: Product. A a [ a owl: Restriction; owl: on. Property mfg: Product_Line; owl: has. Value "Paper machine"]. n By the semantics of the restriction, infer os: Product. A mfg: Product_Line "Paper Machine". n Regardless of how product info is brought into the system, it’s represented consistently in terms of both rdf: type and mfg: Product_line

Challenge: Relationship Transfer in SKOS n When mapping from one model to another, often say something of the form “Everything related to A by property p should also be related to B by property q ” n E. g. , “Everyone who plays for the All Star team is governed by the league’s contract” “Every work in the Collected Works of Shakespeare was written by Shakespeare” n This kind of mapping is relationship transfer: transfer individuals in a relationship with one entity to another relationship with another entity

n Recall the SKOS rule for managing collections Given X skos: narrower C. C skos: member Y. infer X skos: narrower Y. n Where collection C is narrower than concept Y, we can say “Every member of C is narrower than X ” q I. e. , the rule governing skos: narrower in the context of a skos: Collection is a relationship transfer

Challenge 25 n Using OWL constructs, represent the SKOS rule for propagating skos: narrower in the context of skos: Collection n E. g. , represent in OWL the constraint If agro: Milk. By. Source. Animal skos: member Y. then agro: Milk skos: narrower Y.

Solution n First define an inverse of skos: member skos: is. Member. Of owl: inverse. Of skos: member. q n Already have an inverse of skos: narrower in skos: broader Restate the problem with these inverses If Y skos: is. Member. Of agro: Milk. By. Source. Animal. then Y skos: broader agro: Milk.

n To specify that the set of all things Y that are members of agro: Milk. By. Source. Animal, use an owl: has. Value restriction agro: Members. Of. Milk. Source owl: equivalent. Class [ a owl: Restriction; owl: on. Property skos: is. Member. Of; owl: has. Value agro: Milk. By. Source. Animal]. n Also specify the set of all things with agro: Milk as broader category agro: Narrower. Than. Milk owl: equivalent. Class [ a owl: Restriction; owl: on. Property skos: broader; owl: has. Value agro: Milk].

n Next, all members of one class are in the other: agro: Members. Of. Milk. Source rdfs: sub. Class. Of agro: Narrower. Than. Milk. n Think of this rdfs: sub. Class. Of as like an IF/THEN relation n When both subclass and superclass are restrictions, the IF/THEN takes on more meaning, here If an individual skos: is. Member. Of agro: Milk. By. Source. Animal then that individual (has) skos: broader (concept) agro: Milk n With the inverses as defined, this is the same as saying If agro: Milk. By. Source. Animal skos: member X. then agro: Milk skos: narrower X.

Relationship Transfer In FOAF n A similar situation arises in FOAF with groups n Recall that FOAF provides 2 ways to describe members of a group G q Relation foaf: member relates an individual G of foaf: Group to the individuals in G n n The same G is related to an owl: Class by the foaf: membership. Class property Define a foaf: Group for b: Shakespeares_Children as b: Shakespeares_Children a foaf: Group; foaf: name "Shakespeare's Children"; foaf: member b: Susanna, b: Judith, b: Hamnet; foaf: membership. Class b: Child. Of. Shakespeare a owl: Class.
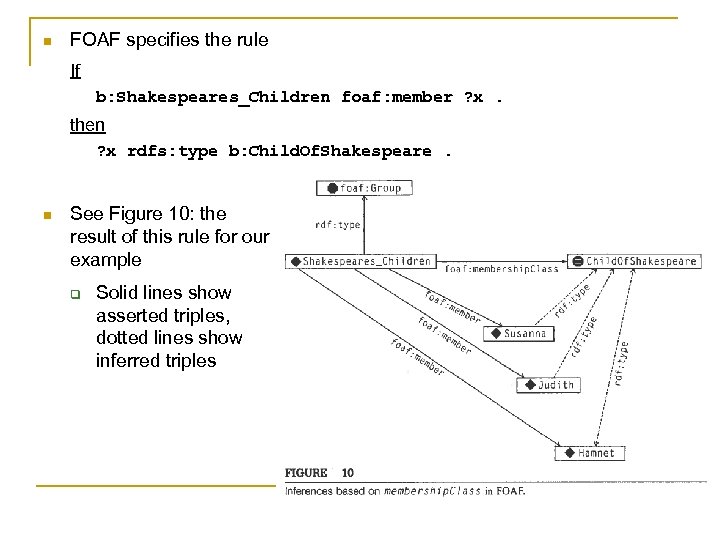
n FOAF specifies the rule If b: Shakespeares_Children foaf: member ? x. then ? x rdfs: type b: Child. Of. Shakespeare. n See Figure 10: the result of this rule for our example q Solid lines show asserted triples, dotted lines show inferred triples

Challenge 26 n How can we get the inference in Figure 10 using only OWL constructs? Solution n This parallels the solution for relationship transfer in SKOS q n But here the relationship we’re transferring to is rdfs: type Begin (as before) by defining an inverse of foaf: member b: member. Of owl: inverse. Of foaf: member. n Using an owl: has. Value restriction, define b: Child. Of. Shakespeare as the class of all those who are b: member. Of b: Shakespeares_Children b: Children. Of. Shakesoeare a owl: Class; rdfs: label "Child of Shakespeare"; owl: equivalent. Class [ a owl: Restriction; owl: has. Value b: Shakespeares_Children; owl: on. Property b: member. Of].

n To follow an inference (see Figure 10), assert a triple b: Shakespeares_Children foaf: member b: Hamlet. n By the semantics of owl: inverse. Of, infer b: Hamnet b: member. Of b: Shakespeares_Children. n This satisfies the conditions of the restriction, so infer b: Hamnet rdf: type b: Child. Of. Shakespeare.

n Turn this inference around backward n Assert instead b: Hamnet rdf: type b: Child. Of. Shakespeare. n By the semantics of owl: equivalent. Class, infer b: Hamnet rdf: type [ a owl: Restriction; owl: has. Value b: Shakespeares_Children; owl: on. Property b: member. Of]. n For b: Hamnet to satisfy the restriction, it must be that b: Hamnet b: member. Of b: Shakespeares_Children. n By the semantics of owl: Inverse. Of, infer b: Shakespeares_Children foaf: member b: Hamlet.

Discussion n That we can represent something in OWL doesn’t necessitate actually doing so n Consider how the solutions just developed compared to those actually taken by the SKOS and FOAF developers n SKOS uses a special-purpose rule to define the meaning of skos: narrower in the context of a skos: Concept and a skos: Collection q So a SKOS user can express the relationship between agro: Milk and agro: Milk. By. Source. Animal just by asserting agro: Milk skos: narrower agro: Milk. By. Source. Animal. q Then the rule takes care of the rest n Simpler for the user than constructing the pair of restrictions

n SKOS in fact defines the rule more generally Given X P C. P rdf: type skos: Collectable. Proeprty. C skos: member Y. infer X P Y. n skos: Collectable. Property includes skos: narrower, skos: broader, skos: related q n So 1 rule expresses constraints for 3 properties To do this with the OWL relationship transfer pattern, we’d have to repeat the pattern once for each property and each concept/collectable pair for which we’re specifying the relationship

n But writing a special-purpose rule into to SKOS description has drawbacks n We need to define a rule language and a processor for the rules n The pragmatic answer: q q n Rules are written in the natural language used for the specification Processing is done by each application rather than by a generalpurpose inference engine In contrast, an OWL solution q q n uses generic software exploits standard semantics The SKOS specification expresses this rule in prose , leaving its implementation to each application

n With FOAF, unlike SKOS, there’s only one property (foaf: membership. Class) affected by the transfer rule n And, in FOAF, a user just asserts one triple b: Shakespeares_Children foaf: membership. Class b: Child. Of. Shakespeare. for the transfer rule to come into play q q n This isn’t built into some other construct, like skos: Collection The FOAF user explicitly indicates where the rule is invoked The ground-up evolutionary strategy of FOAF argues against special -purpose meanings in the specification q Things might change or be superseded

n Any FOAF user can already express in OWL the relationship between a foaf: Group and its foaf: members q n Or between any class and property as needed This agrees with q q n the AAA slogan and the ground-up empowerment of the FOAF user community The SKOS effort is controlled by committee q n Can put rules into its specification and control how they interact And SKOS is intended to be used across many domains q SKOS must anticipate that any number of concept/collection pairs might need this rule

n In a narrower (“vertical”) domain, some of these conditions may not apply q q n Most modelers don’t seek W 3 C recommendation status or other approval as a standard Rules put into the model might adversely interact with other rules Often in a vertical domain there are few distinguished instances where some part of the model is replicated in another place q q Then the relationship transfer is part of the description of these concepts No need to be repeated indefinitely often

n In such cases, it may be just as convenient to describe the relationships using OWL constructs n Thus, for group membership in OWL, the modeler makes a very special statement about a group when relating it to its membership. Class n Might accept a quite involved way to express this relationship q Especially if done without cluttering the FOAF model itself

Regarding modeling in general n One reason to model knowledge in a domain in the first place is to understand q q n the ramifications of a model where there are conflicts between one view of the world another When rules are represented as part of a practice (e. g. , encoded into a standard), the rules themselves aren’t available for automated analysis q E. g. , suppose a FOAF rule interacted adversely with a SKOS rule n n How would we know not to use the 2 models together? Later introduce notions of inconsistency and contradiction q See how representations that follow the OWL standard can detect such interactions before their application

Alternative Descriptions of Restrictions n Consider traditional terminology sometimes used in talking about OWL restrictions and classes q rdfs: sub. Class. Of can be understood as an if-then relation n q X rdfs: cub. Class. Of Y “means” if something is an X then it’s a Y rdfs: equivalent. Class can be understood as an if-and-only-if (iff) relation n Given If p then q q p is said to be a sufficient condition for q q q is a necessary condition for p and a partial definition of it

n Given p iff q q q n p is said to be a necessary and sufficient condition of q And q is a necessary and sufficient condition of p Stick with the OWL terminology q Avoid thorny issues associated with natural language
a34ec1304dd89b9249b4730b85e190a7.ppt