4a8c980531b0221646a894c4de1e7b2d.ppt
- Количество слайдов: 29

Basic Concepts Gene, Allele, Genotype, and Phenotype A pair of chromosomes Father Mother Phenotype Subject Gene A, with two alleles A and a Genotype Height IQ 1 2 AA AA 185 182 100 104 3 4 Aa Aa 175 171 103 102 5 6 aa aa 152 155 103 101
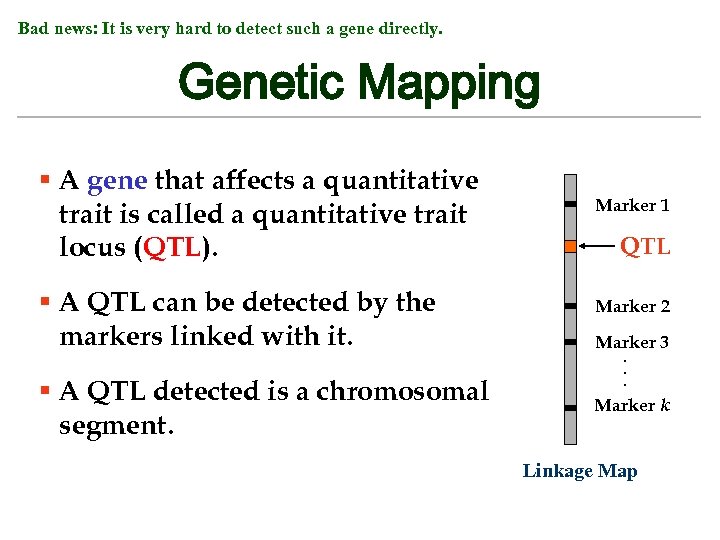
Bad news: It is very hard to detect such a gene directly. Genetic Mapping § A gene that affects a quantitative trait is called a quantitative trait locus (QTL). § A QTL can be detected by the markers linked with it. § A QTL detected is a chromosomal segment. Marker 1 QTL Marker 2 Marker 3. . . Marker k Linkage Map

QTL Mapping in Natural Populations • Basic theory for QTL mapping is derived from linkage analysis in controlled crosses • There is a group of species in which it is not possible to make crosses • QTL mapping in such species should be based on existing populations
Human Chromosomes Male Xy X y Female XX Xy Daughter Son

Human Difference

How many genes control human body height?

Discontinuous Distribution due to a single dwarf gene

Continuous Distribution due to many genes?
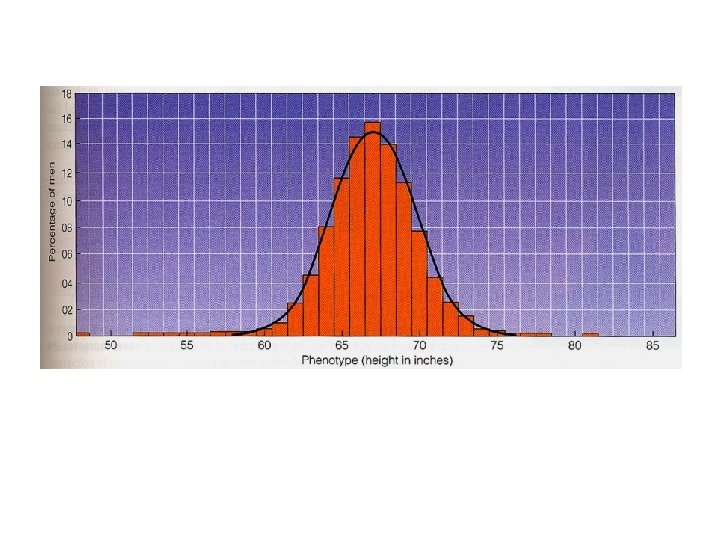

Continuous Variation due to • Polygenes 31=3, 32=9, …, 310=59, 049 • Environmental modifications • Gene-environmental interactions

Power statistical methods are crucial for the identification of human height genes
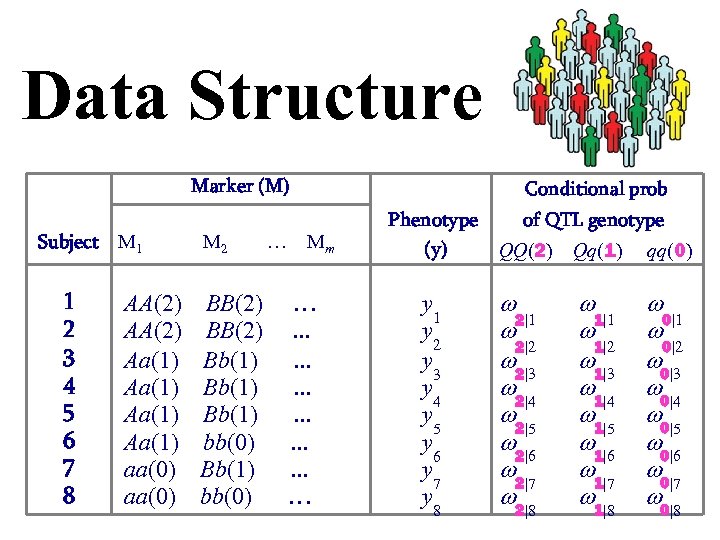
Data Structure Marker (M) Subject M 1 1 2 3 4 5 6 7 8 AA(2) Aa(1) aa(0) M 2 BB(2) Bb(1) bb(0) … Conditional prob Mm …. . . . … Phenotype of QTL genotype (y) QQ(2) Qq(1) qq(0) y 1 y 2 y 3 y 4 y 5 y 6 y 7 y 8 2|1 2|2 2|3 2|4 2|5 2|6 2|7 2|8 1|1 1|2 1|3 1|4 1|5 1|6 1|7 1|8 0|1 0|2 0|3 0|4 0|5 0|6 0|7 0|8

Linkage disequilibrium mapping – natural population Association between marker and QTL -Marker, Prob(M)=p, Prob(m)=1 -p -QTL, Prob(A)=q, Prob(a)=1 -q Four haplotypes: Prob(MA)=p 11=pq+D Prob(Ma)=p 10=p(1 -q)-D Prob(m. A)=p 01=(1 -p)q-D Prob(ma)=p 00=(1 -p)(1 -q)+D p=p 11+p 10 q=p 11+p 01 D=p 11 p 00 -p 10 p 01

Joint and conditional ( j|i) genotype prob. between marker and QTL AA Aa aa Obs MM Mm mm p 112 2 p 11 p 012 2 p 11 p 10 2(p 11 p 00+p 10 p 01) 2 p 01 p 00 p 102 2 p 10 p 002 n 1 n 0 MM p 112 p 2 2 p 11 p 01 2 p(1 -p) p 012 (1 -p)2 2 p 11 p 10 p 2 2(p 11 p 00+p 10 p 01) 2 p(1 -p) 2 p 01 p 00 (1 -p)2 p 102 p 2 2 p 10 p 00 2 p(1 -p) p 002 n 2 Mm mm n 1 n 0

Linkage disequilibrium mapping – natural population Mixture model-based likelihood with marker information L( |y, M)= i=1 n[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Prior prob. Sam- Height ple (cm, y) 1 184 2 185 3 180 4 182 5 167 6 169 7 165 8 166 Marker genotype M MM (2) Mm (1) mm (0) QTL genotype AA Aa 2|1 1|1 2|2 1|2 2|3 1|3 2|4 1|4 2|5 1|5 2|6 1|6 2|7 1|7 2|8 1|8 aa 0|1 0|2 0|3 0|4 0|5 0|6 0|7 0|8

Linkage disequilibrium mapping – natural population Conditional probabilities of the QTL genotypes (missing) based on marker genotypes (observed) L( |y, M) = i=1 n [ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] = i=1 n 2 [ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Conditional on 2 (n 2) i=1 n 1 [ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Conditional on 1 (n 1) i=1 n 0 [ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Conditional on 0 (n 0)

Linkage disequilibrium mapping – natural population Normal distributions of phenotypic values for each QTL genotype group f 2(yi) = 1/(2 2)1/2 exp[-(yi- 2)2/(2 2)], 2 = + a f 1(yi) = 1/(2 2)1/2 exp[-(yi- 1)2/(2 2)], 1 = + d f 0(yi) = 1/(2 2)1/2 exp[-(yi- 0)2/(2 2)], 0 = - a

Linkage disequilibrium mapping – natural population Differentiating L with respect to each unknown parameter, setting derivatives equal zero and solving the log-likelihood equations L( |y, M) = i=1 n[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] log L( |y, M) = i=1 n log[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] Define 2|i = 2|if 1(yi)/[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] 1|i = 1|if 1(yi)/[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] 0|i = 0|if 1(yi)/[ 2|if 2(yi) + 1|if 1(yi) + 0|if 0(yi)] (1) (2) (3) 2 = i=1 n( 2|iyi)/ i=1 n 2|i 1 = i=1 n( 1|iyi)/ i=1 n 1|i 0 = i=1 n( 0|iyi)/ i=1 n 0|i 2 = 1/n i=1 n[ 2|i(yi- 2)2+ 1|i(yi- 1)2+ 0|i(yi- 0)2] (4) (5) (6) (7)
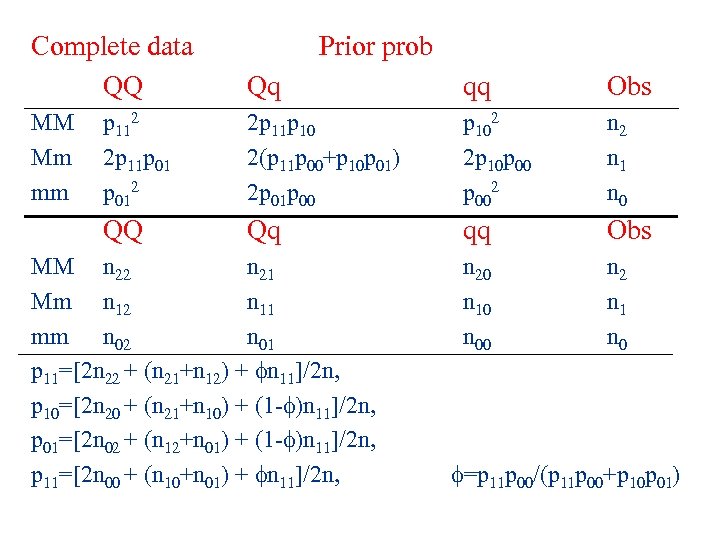
Complete data QQ Prior prob Qq qq Obs MM Mm mm p 112 2 p 11 p 012 2 p 11 p 10 2(p 11 p 00+p 10 p 01) 2 p 01 p 00 p 102 2 p 10 p 002 n 1 n 0 QQ Qq qq Obs n 20 n 10 n 00 n 2 n 1 n 0 MM n 22 n 21 Mm n 12 n 11 mm n 02 n 01 p 11=[2 n 22 + (n 21+n 12) + n 11]/2 n, p 10=[2 n 20 + (n 21+n 10) + (1 - )n 11]/2 n, p 01=[2 n 02 + (n 12+n 01) + (1 - )n 11]/2 n, p 11=[2 n 00 + (n 10+n 01) + n 11]/2 n, =p 11 p 00/(p 11 p 00+p 10 p 01)

Incomplete (observed) data Posterior prob QQ Qq qq Obs MM 2|i Mm 2|i mm 2|i n 2 n 1 n 0 1|i 1|i 0|i 0|i p 11=[ i=1 n 2(2 2|i+ 1|i)+ i=1 n 1( 2|i+ 1|i)]/2 n, p 10={ i=1 n 2(2 0|i+ 1|i)+ i=1 n 1[ 0|i+(1 - ) 1|i]}/2 n, p 01={ i=1 n 0(2 2|i+ 1|i)+ i=1 n 1[ 2|i+(1 - ) 1|i]}/2 n, p 00=[ i=1 n 2(2 0|i+ 1|i)+ i=1 n 1( 0|i+ 1|i)]/2 n (8) (9) (10) (11)

EM algorithm (1) Give initiate values (0) =( 2, 1, 0, 2, p 11, p 10, p 01, p 00)(0) (2) Calculate 2|i(1), 1|i(1) and 0|i(1) using Eqs. 1 -3, (3) Calculate (1) using 2|i(1), 1|i(1) and 0|i(1) based on Eqs. 4 -11, (4) Repeat (2) and (3) until convergence.

Hypothesis Tests • Is there a significant QTL? H 0: μ 2 = μ 1 H 1: Not H 0 LR 1 = -2[ln L 0 – L 1] Critical threshold determined from permutation tests

Hypothesis Tests • Can this QTL be detected by the marker? H 0: D = 0 H 1: Not H 0 LR 2 = -2[ln L 0 – L 1] Critical threshold determined from chi-square table (df = 1)

A case study from human populations • 105 black women and 538 white women; • 10 SNPs genotyped within 5 candidates for human obesity; • Two obesity traits, the amount of body fat (body mass index, BMI) and its distribution throughout the body (waist to hip circumference ratio, WHR)


Objective Detect quantitative trait nucleotides (QTNs) predisposing to human obesity traits, BMI and WHR
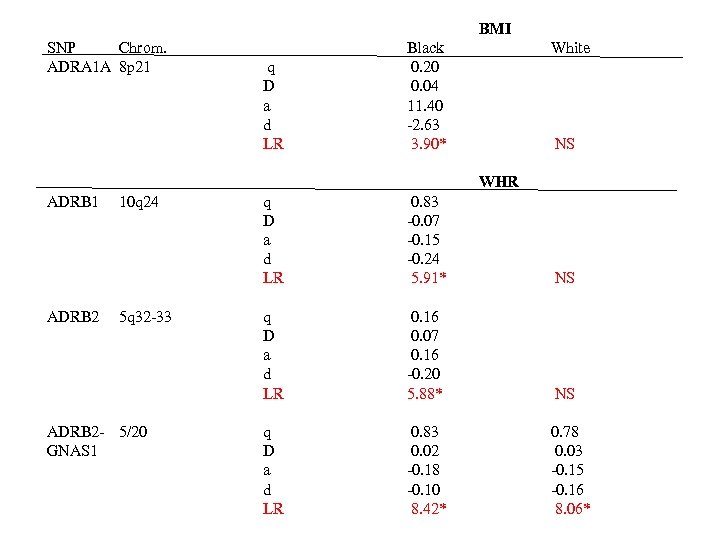
BMI SNP Chrom. ADRA 1 A 8 p 21 q D a d LR Black 0. 20 0. 04 11. 40 -2. 63 3. 90* White NS WHR ADRB 1 ADRB 2 10 q 24 5 q 32 -33 ADRB 2 - 5/20 GNAS 1 q D a d LR 0. 83 -0. 07 -0. 15 -0. 24 5. 91* NS q D a d LR 0. 16 0. 07 0. 16 -0. 20 5. 88* NS q D a d LR 0. 83 0. 02 -0. 18 -0. 10 8. 42* 0. 78 0. 03 -0. 15 -0. 16 8. 06*

Shape mapping meets LD mapping Mapping Body Shape Genes through Shape Mapping Ningtao Wang, Yaqun Wang, Zhong Wang, Han Hao and Rongling Wu* Center for Statistical Genetics, The Pennsylvania State University, Hershey, PA 17033, USA J Biom Biostat 2012, 3: 8
4a8c980531b0221646a894c4de1e7b2d.ppt