c9c3bd51de4f14dfadfee296a3634af2.ppt
- Количество слайдов: 36

BAROCLINIC & BAROTROPIC INSTABILITIES

BAROCLINIC & BAROTROPIC INSTABILITIES INSTABILITY - TYPES. (A) PARCEL METHOD. (I) (II) INERTIAL. (III) (B) STATIC. SYMMETRIC. WAVE METHOD. (I) AMPLITUDE SHOULD GROW. (II) SOURCE TO FEED MUST. (III) SOURCE IS SHEAR OF BASIC TO FLOW. (IV) SHEAR ‘H’ OR ‘V’, STRONG WIND – K. E.

BAROCLINIC & BAROTROPIC INSTABILITIES BAROTROPIC & BAROCLINIC CONCEPT. (A) TO BASIC FLOW MUST GIVE UP PE AND / OR KE PERTURBATION FOR ITS GROWTH. (B) BAROTROPIC. PERTURBATION DRAWS ENERGY FROM KE OF THE BASIC FLOW (HORIZONTAL WIND SHEAR) (C) BAROCLINIC. BASIC STATE FLOW PE IS CONVERTED INTO PE & KE OF PERTURBATION.

BAROCLINIC & BAROTROPIC INSTABILITIES BAROTROPIC INSTABILITY. (A) DENSITY IS CONSTANT AT ANY ISOBARIC LEVEL. (B) NO VERTICAL SHEAR. (C) NO THERMAL WIND. (D) DRAWS ENERGY BY EDDY TRANSPORT OF MOMENTUM. (E) ONLY HORIZONTAL SHEAR IS ZONAL SHEAR. (F) NECESSARY CONDITION: GRADIENT OF ABSOLUTE VORTICITY MUST VANISH IN THE REGION AT SOME POINT. i. e. ∂(ζ+ f)/ ∂y = 0.

BAROTROPIC INSTABILITY 1. THIS TYPE OF INSTABILITY ARISES MAINLY FROM EXCESSIVE HORIZONTAL SHEAR OF FLOW, FOR EXAMPLE IN A JET. 2. EXCHANGES OF KINETIC ENERGY TAKES PLACE BETWEEN THE BASIC FLOW AND THE WAVE PERTURBATIONS THROUGH HORIZONTAL NON-DIVERGENT MOTIONS. IN THE PROCESS, THE ZONAL JET GETS DILUTED, ITS MOMENTUM IS SHARED BY ITS ADJACENT LAYERS. WHILE THE ZONAL MOMENTUM OF THE JET FLOW AS A WHOLE IS CONSERVED, ITS KINETIC ENERGY DECREASES. 3. THIS LOSS OF KINETIC ENERGY BY THE JET IS GAINED BY THE WAVE PERTURBATION

BAROTROPIC INSTABILITY 3. THE STABILITY OF THE FLOW DEPENDS ON THE TYPE OF THE HORIZONTAL SHEAR. 4. THE FLOW WOULD BE UNSTABLE IF THE SHEAR VORTICITY HAS A MATHEMATICAL MAXIMUM IN THE REGION. 5. IN THIS TYPE OF FLOW, THERE IS EXCHANGE OF KINETIC ENERGY BETWEEN THE BASIC LINEAR FLOW AND THE SINUSOIDAL PERTURBATION. THERE IS NO CONVERSION BETWEEN POTENTIAL AND KINETIC ENERGY. 6. AT CRITICAL POINT y = yk , β - ∂2 U/∂y 2 = 0

BAROCLINIC INSTABILITY 1. THIS TYPE OF INSTABILITY ARISES FROM COMBINATION OF VERTICAL SHEAR AND ROTATION. A 2. IN A BALANCED STATE, VERTICAL SHEAR OF HORIZONTAL WIND, SAY ZONAL WIND U, IMPLIES MERIDIONAL GRADIENT OF TEMPERATURE. 3. IF THE WESTERLIES INCREASE WITH HEIGHT IN A BALANCES STATE, THERMAL WIND EQUATION TELLS US THAT TEMPERATURE DECREASES POLEWARDS. THERE IS ZONAL AVAILABLE POTENTIAL ENERGY AZ IN THE ATMOSPHERE. 4. THIS AZ CAN GET ACCUMULATED IN THE ATMOSPHERE ONLY UPTO A CERTAIN EXTENT.

BAROCLINIC INSTABILITY 5. BEYOND THAT, THE EQUILIBRIUM IS READY TO BREAK DOWN AT THE SLIGHEST PROVOCATION. IN A PERTURBATION SUPERIMPOSED ON THID BASIC STATE, COLD POLAR AIR FLOWS EQUATORWARD AND THE RELATIVELY WARM SUB-TROPICAL AIR FLOWS POLEWARD SO THAT ALONG A LATITUDE CIRCLE, WE HAVE NOW COLD AND WARM AIR SIDE BY SIDE. 6. AZ IS CONVERTED IN TO AE. GENERALLY, A SITUATION PREVAILS IN WHICH WARM AIR RISES AND COLD AIR SINKS IN x-p PLANE. AE IS CONVERTED INTO KE. AZ AE KE

BAROCLINIC INSTABILITY 7. THE STORE HOUSE OF AZ IS CONTINUOUSLY FED BY DIFFERENTIAL HEATING OF DIFFERENT LATITUDE ZONES FOR WHICH SOLAR HEATING IS THE ULTIMATE CAUSE. KE IS CONTINUOUSLY DRAINED OUT OF THE SYSTEM BY FRICTION.

BAROCLINIC & BAROTROPIC INSTABILITIES Baroclinic Instability (A) CONVERSION OF PE OF THE BASIC FLOW TO PE / KE OF EDDY. (B) VERTICAL SHEAR, TEMPERATURE GRADIENT AND THERMAL WIND ARE ESSENTIAL. (C) VERTICAL PLANE, THEREFORE INSTEAD OF ABSOLUTE VORTICITY (ζ +f), WE USE POTENTIAL VORTICITY CONCEPT i. e. GRADIENT OF POTENTIAL VORTICITY MUST VANISH TO GIVE MAX / MIN WITHIN THE DOMAIN i. e. ∂ [(ζ +f)/ ∆H]/ ∂y = 0 i. e. MAXIMUM OR MINIMUM MUST EXIST WITHIN THE DOMAIN. Ascertained by (a) ∂u / ∂z = 0 or ∂q / ∂y = 0 (b) ∂u / ∂z < 0 or ∂q / ∂y < 0 (c) ∂u / ∂z > 0 or ∂q / ∂y > 0 where q is mean potential vorticity of the column

BAROCLINIC & BAROTROPIC INSTABILITIES Barotropic Baroclinic 1. Instability (a) Meridional shear in zonal flow is relevant. (b) No thermal wind concept. 1. Instability (a) Vertical shear of zonal or meridional wind is applicable (du/dz) or (dv/dz). (b) Shear is represented by thermal wind (∂Vg/∂z). 2. Waves increase/ derive their K. E. as a result of vorticity transport. 2. Waves grow as a result of conversion of P. E. due to baroclinicity in to K. E. 3. β- (∂2 u/∂y 2) = 0, somewhere in the domain. 3. Instability gives unstable wave when root mean square of thermal wind exceeds Rossby wave. 4. Depends upon the concentration of wind and strength of β. 4. Depends upon concentration of temperature with respect to height and strength of wind with height.

BAROCLINIC & BAROTROPIC INSTABILITIES Barotropic Baroclinic 5. There will be no unstable wave if (U 0/β L) < (4/3√ 3 ); U 0 is zonal wind. 5. Waves shall become unstable when critical limits of du/dz and (∂T/∂y) are surpassed. 6. Unstable Wavelengths: more than 300 km and less than 2500 km maximum growth rate is 2000 km. 6. Unstable Wavelength: not less than 2000 km & not more than 8000 km. Maximum growth rate for λ = 2500 – 3000 km. 7. Temperature gradient is very small; so no such criterion exists, although Easterly wave troughs are examined in relation to their temperature characteristics and genesis of tropical cyclones. 7. Temperature wave should lag behind the pressure wave for developing wave and temperature wave precede pressure wave for decaying systems. Cold trough travel slower than surface zonal flow.

BAROCLINIC & BAROTROPIC INSTABILITIES Barotropic Baroclinic 8. Zone of interest: Near ITCZ or equatorial shear line with perturbations in trades. 8. Near PFJ or STJ when sharply inclined with perturbations in mid lat westerlies and short waves. 9. Momentum transport and meridional scale. 9. Heat transports and vertical scale. 10. Meridional shear exceeding critical value associated with easterly wave or LLT in trades giving rise to unstable perturbations (growth of tropical cyclones). 10. Under sub-critical conditions sinusoidal waves are likely to continue without breaking down. 11. LLJ, ASJ (Australian Jet) or African jet gives rise to such instability. 11. PFJ / STJ reinforce the instability. 12. No wave formation of its own. 12. Wave formation is possible.

BAROTROPIC INSTABILITIES HERE, IT IS WORTHWHILE TO QUOTE ARNASON (1963): 1. BAROCLINIC PERTURBATIONS ARE MUCH LESS LIKELY TO OCCUR AT LOW LATITUDES THAN AT MIDDLE OR HIGH LATITUDES. 2. TO THE EXTENT THAT BAROCLINIC PERTURBATIONS DO OCCUR IN THE TROPICS, THEY ARE PRESUMABLY SHALLOW AND GROW SLOWLY BECAUSE OF THE SMALL WIND SHEAR.

BAROTROPIC INSTABILITIES 3. IF WE ALLOW FOR RELEASE OF ENERGY THROUGH CONDENSATION IN THE BASIC FLOW, SYNOPTIC-SCALE PERTURBATIONS ARE MORE LIKELY TO OCCUR THAN UNDER DRY ADIABATIC CONDITIONS. 4. THE BASIC FLOW WITHIN THE ITCZ IS PROBABLY AT TIMES CLOSE TO SATURATION OWING TO LARGE ASCENT BY THE ZONE’S OVER-ALL CONVERGENCE OR INCLUDED BY UPPER AIR LARGE-SCALE DISTURBANCES”.

BAROTROPIC INSTABILITIES 5. IF LOW-LEVEL PERTURBATIONS ARE FORMED WITHIN THIS ZONE, THE ASSOCIATED ASCENT OF AIR MAY RESEMBLE THOSE POSTULATED BY SETTING h = 0 (NEUTRAL STATIC STABILITY). 6. THE TROPICAL ATMOSPHERE IS STATICALLY UNSTABLE FOR MOIST-ADIABATIC ASCENT UP TO ABOUT 500 HPA DURING THE HURRICANE SEASON WHICH ACCOUNTS FOR WIDESPREAD SHOWER ACTIVITIES.

BAROTROPIC INSTABILITIES 7. AS SHOWN BY HAQUE (1952), LILLY (1960) & KUO (1961), THE PREFERRED SCALE IN THIS CASE THAT OF A CUMULUS CLOUD, AND THE RELEASE OF LATENT HEAT DOES NOT LEAD TO THE AMPLIFICATION OF SYNOPTICSCALE SYSTEMS IN THE ABSENCE OF VERTICAL WIND SHEAR. THE OCCURRENCE OF A SLIGHT WIND SHEAR, APPROXIMATELY IN GEOSTROPHIC BALANCE, MAY CONSIDERABLY CHANGE THIS PICTURE, SINCE A SYNOPTIC-SCALE SYSTEM WOULD NOW DRAW KINETIC ENERGY FROM A NEW SOURCE AND NOT DEPEND ON THE RELEASE OF LATENT HEAT ALONE. ONCE SUCH A SYSTEM IS FORMED, THE ORGANIZED LARGE-SCALE RELEASE OF LATENT HEAT MAY BE INSTRUMENTAL IN THE FURTHER DEVELOPMENT.

BAROTROPIC INSTABILITIES 8. LATER RESEARCH STUDIES HAVE PROVED THAT EVEN IN THE EXTRA-TROPICAL REGIONS, LATENT HEAT RELEASE (LHR) SUPPLEMENTS THE ACTION OF VERTICAL SHEARS IN THE CLASSICAL THEORY OF BAROCLINIC INSTABILITY AND ENHANCES THE GROWTH RATE OF EXTRA-TROPICAL CYCLONE WAVES. AMONG OTHERS, PAULEY & SMITH (1988) SUGGESTED THAT LHR IS IMPORTANT AND HAS “DIRECT” AND “INDIRECT” EFFECTS FAVOURING EXTRA-TROPICAL CYCLOGENESIS. AMONG THE DIRECT EFFECTS, THEY COUNTED GENERATION OF AVAILABLE POTENTIAL ENERGY AND HEIGHT TENDENCIES, FORCED BY DIABATIC HEATING RELEASED DURING CONDENSATION. THEY ALSO POINTED OUT THAT INDIRECTLY LHR INFLUENCES SEVERAL PHYSICAL PARAMETERS LIKE TEMPERATURE, GEOPOTENTIAL HEIGHT, WIND SPEED AND VERTICAL MOTION WITH THE HELP IN THE BAROCLINIC CONVERSION OF EDDY AVAILABLE POTENTIAL TO EDDY KINETIC ENERGY DURING THE EVOLUTION OF THE SYNOPTIC-SCALE WAVE MOTION.

BAROTROPIC INSTABILITIES 9. DUE TO SUCH IMPORTANCE OF LATENT HEAT RELEASE IN THE LIFE-CYCLE OF TROPICAL AS WELL AS EXTRA-TROPICAL LOW PRESSURE SYSTEMS, IT IS WORTH WHILE TO LOOK FOR THE PARAMETER WHICH COULD GIVE AN INSIGHT INTO THE WAY IN WHICH LATENT HEAT RELEASE INFLUENCES CYCLOGENESIS IN TROPICAL AS WELL AS EXTRA-TROPICAL LATITUDES. PERHAPS, “EFFECTIVE STATIC STABILITY” COULD PROVIDE SOME INSIGHT INTO THIS PHENOMENON.

BAROTROPIC INSTABILITIES • Kuo’s main results are qualitatively illustrated in the diagram, the abscissa denotes the wavelength L. • The ordinate for continuous curve denotes CR, the real part of C. The ordinate for broken line denotes CI, the imaginary part of C. The interpretation of the diagram is in terms of different wavelengths.

BAROTROPIC INSTABILITIES

BAROTROPIC INSTABILITIES • For L = Lk, ci = 0 , cr = Uk. The wave is neutral. It moves with a phase velocity Uk which is equal to the velocity of the basic current at that point. • For L < Lk, ci < 0 , cr > Uk. The waves are damped. They move faster than the basic zonal current at the critical point. • For Lk < L 0, ci > 0 , U 0 < cr < Uk. The waves are unstable, they amplify. For unstable waves, Lk is the short wave cut-off and L 0 is the long wave cut-off. The phase velocity lies between the zonal current velocity at the critical point and the minimum velocity of the zonal current in the latitudinal belt under consideration. The perturbation has its maximum amplitude at the mid-point of the belt where the zonal wind velocity is maximum.

BAROTROPIC INSTABILY • For L 0 < L, ci = 0 , cr = U 0. These long waves are neutral and move slower than the slowest current in the latitudinal belt under consideration. • There are no neutral waves which have a phase velocity greater than the maximum zonal westerly wind velocity in the symmetric belt under consideration. On the other hand, neutral waves may have a phase velocity less than the minimum wind velocity in the same belt under consideration. • For neutral waves, the wave troughs and ridges are untilted and run in North-South direction. For unstable waves in the Northern Hemispheric westerlies, the trough lines will be tilted in the direction from SE to NW to the south of the point of minimum absolute vorticity, and from SW to NE to the north of the point of maximum absolute vorticity.

BAROCLINIC INSTABILY Wien - Nielsen’s Conclusions. (a) Mid–latitude westerlies are always unstable with respect to the disturbances of the type considered here, particularly during winter and, to a minor degree, also in summer (see figure for a typical value of 7. 3 mps). (b) The static stability is the main reason for the stable behaviour of sufficiently short waves (region to the left of the separation line AB in figure). (c) The stable behaviour of long wave is due to the stabilizing effect of the Rossby parameter (Planetary control). As these theoretical conclusions agree quite well with the observed behaviour of upper waves, one may assume that the rather simple two-level atmospheric model is a reasonable approximation to the simple state of the mid-latitude atmosphere. Now a days exist much more sophisticated multi-layered atmospheric models, which produce on even better resemblance to the physical state of the atmosphere.
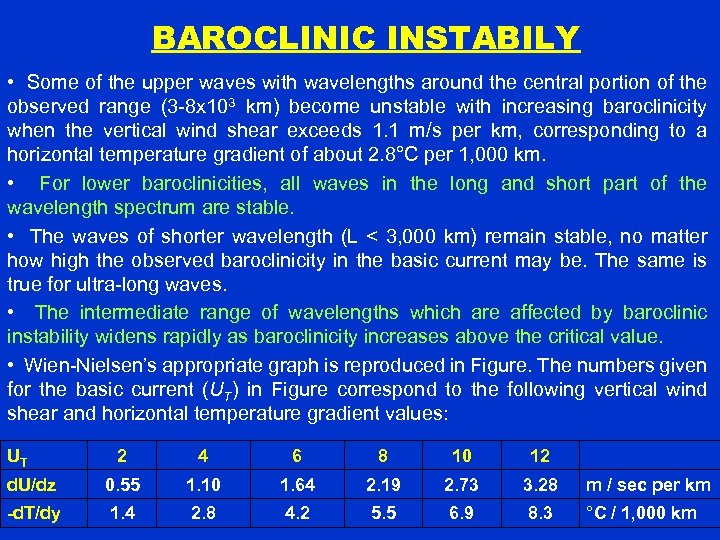
BAROCLINIC INSTABILY • Some of the upper waves with wavelengths around the central portion of the observed range (3 -8 x 103 km) become unstable with increasing baroclinicity when the vertical wind shear exceeds 1. 1 m/s per km, corresponding to a horizontal temperature gradient of about 2. 8°C per 1, 000 km. • For lower baroclinicities, all waves in the long and short part of the wavelength spectrum are stable. • The waves of shorter wavelength (L < 3, 000 km) remain stable, no matter how high the observed baroclinicity in the basic current may be. The same is true for ultra-long waves. • The intermediate range of wavelengths which are affected by baroclinic instability widens rapidly as baroclinicity increases above the critical value. • Wien-Nielsen’s appropriate graph is reproduced in Figure. The numbers given for the basic current (UT) in Figure correspond to the following vertical wind shear and horizontal temperature gradient values: UT 2 4 6 8 10 12 d. U/dz 0. 55 1. 10 1. 64 2. 19 2. 73 3. 28 m / sec per km -d. T/dy 1. 4 2. 8 4. 2 5. 5 6. 9 8. 3 °C / 1, 000 km
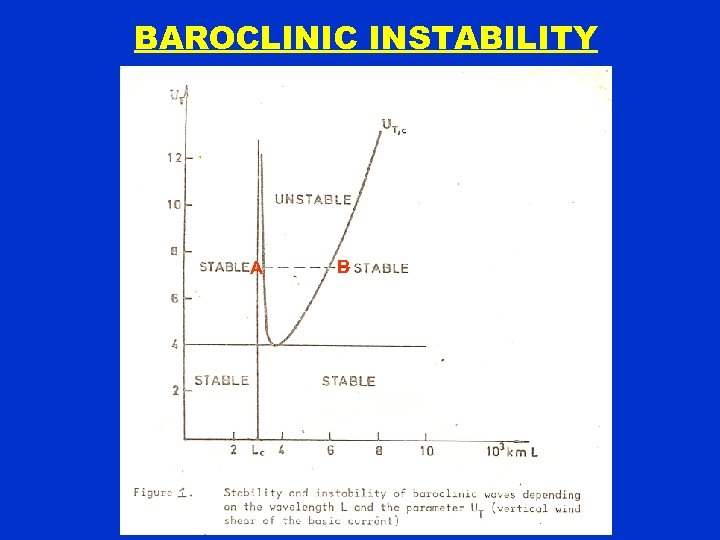
BAROCLINIC INSTABILITY A B
BAROCLINIC INSTABILITY

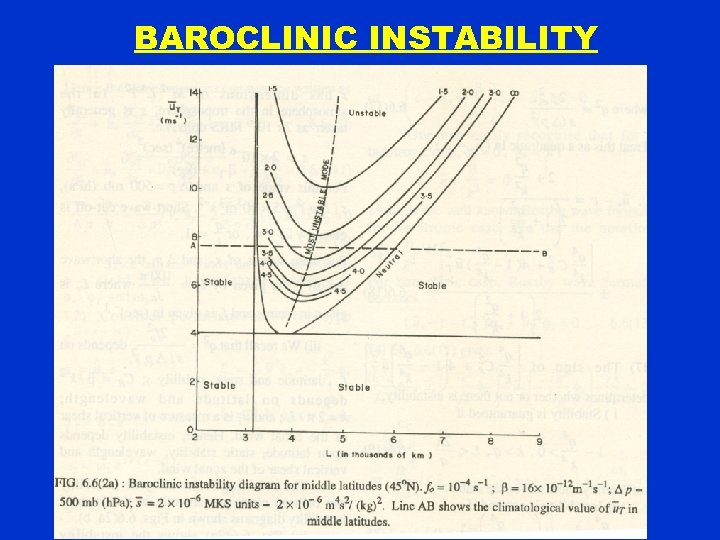
BAROCLINIC INSTABILITY • For any given value of u. T, say 6 ms-1, we may draw a line parallel to the x-axis. For this value of u. T, all wave lengths less than about 3, 270 km and all wavelengths greater than about 5, 300 km are stable; the wavelengths between 3, 270 and 5, 300 km are all unstable. The wavelength of about 4, 100 km is the most unstable wavelength, with e-folding time of about 3. 5 days. • For u. T = 10 ms-1, all wavelengths between 3, 200 km and 7, 000 km are unstable, the most unstable wavelength being 4, 600 km, with e-folding time of 1. 5 days.

BAROCLINIC INSTABILITY Conventional interpretation of this instability diagram: - • For a given value of u. T, there is a whole spectrum of unstable wavelengths. In nature, any perturbation in xdirection can be decomposed in a series of wave components, the most unstable wavelength has the fastest rate of growth and will ultimately prevail in the atmosphere. • All wavelengths shorter than 3142 km are stable. All vertical shears with u. T, less than 4 ms-1 are also stable.

BAROCLINIC INSTABILITY 1. SHORT WAVE CUT-OFF. THE SHORTEST WAVELENGTH GIVEN BY THE NEUTRAL CURVE; ALL WAVELENGTHS SHORTER THAN THIS WAVELENGTH ARE STABLE. 2. LONG WAVE CUT-OFF. THE LONGEST WAVELENGTH GIVEN BY THE NEUTRAL CURVE; ALL WAVELENGTHS LONGER THAN THIS WAVELENGTH ARE STABLE. 3. GROWTH RATE. (A) STATIC STABILITY IS RESPONSIBLE FOR SHORT WAVE CUT OFF. (B) Β-TERM IS RESPONSIBLE FOR LONG-WAVE CUT-OFF. (C) GROWTH RATES INCREASE WITH INCREASE IN VERTICAL SHEAR OF THE ZONAL CURRENT.

BAROTROPIC & BAROCLINIC INSTABILITIES Barotropic – Baroclinic – CISK Mechanism • THE PRIMARY ROLE OF TERRAIN (HIMALAYAS) IS TO PRODUCE A MEAN CIRCULATION WHICH IS BAROTROPICALLY UNSTABLE AT THE LOW LEVELS AND PROVIDES TRIGGERING MECHANISM FOR THE MONSOON DEPRESSION. • THE DOMINANT ENERGY FOR TRANSFORMATION IS THE EDDY AVAILABLE POTENTIAL ENERGY TO EDDY KINETIC ENERGY. THE PRIMARY SOURCE IS CONDENSATION HEATING. THE BAROCLINIC INSTABILITY PLAYS A ROLE. • THE PERTURBATION IS DRIVEN PRIMARILY BY CUMULUS HEATING. THE MAGNITUDE OF GROWTH RATES AND THE DOMINANT ENERGY TRANSFORMATIONS ARE DETERMINED BY CISK.

THANK YOU

BAROTROPIC INSTABILITY 1. THIS TYPE OF INSTABILITY ARISES MAINLY FROM EXCESSIVE HORIZONTAL SHEAR OF FLOW, FOR EXAMPLE IN A JET. 2. EXCHANGES OF KINETIC ENERGY TAKES PLACE BETWEEN THE BASIC FLOW AND THE WAVE PERTURBATIONS THROUGH HORIZONTAL NON-DIVERGENT MOTIONS. TH THE PROCESS, THE ZONAL JET GETS DILUTED, ITS MOMENTUM IS SHARED BY ITS ADJACENT LAYERS. WHILE THE ZONAL MOMENTUM OF THE JET FLOW AS A WHOLE IS CONSERVED, ITS KINETIC ENERGY DECREASES. 3. THIS LOSS OF KINETIC ENERGY BY THE JET IS GAINED BY THE WAVE PERTURBATION

BAROTROPIC INSTABILITY 3. THE STABILITY OF THE FLOW DEPENDS ON THE TYPE OF THE HORIZONTAL SHEAR. 4. THE FLOW WOULD BE UNSTABLE IF THE SHEAR VORTICITY HAS A MATHEMATICAL MAXIMUM IN THE REGION. 5. IN THIS TYPE OF FLOW, THERE IS EXCHANGE OF KINETIC ENERGY BETWEEN THE BASIC LINEAR FLOW AND THE SINUSOIDAL PERTURBATION. THERE IS NO CONVERSION BETWEEN POTENTIAL AND KINETIC ENERGY. 6. At critical point y = yk , β - ∂2 U/∂y 2 = 0

BAROCLINIC INSTABILITY 1. THIS TYPE OF INSTABILITY ARISES FROM COMBINATION OF VERTICAL SHEAR AND ROTATION. A 2. IN A BALANCED STATE, VERTICAL SHEAR OF HORIZONTAL WIND, SAY ZONAL WIND U, IMPLIES MERIDIONAL GRADIENT OF TEMPERATURE. 3. IF THE WESTERLIES INCREASE WITH HEIGHT IN A BALANCES STATE, THERMAL WIND EQUATION TELLS US THAT TEMPERATURE DECREASES POLEWARDS. THERE IS ZONAL AVAILABLE POTENTIAL ENERGY AZ IN THE ATMOSPHERE. 4. THIS AZ CAN GET ACCUMULATED IN THE ATMOSPHERE ONLY UPTO A CERTAIN EXTENT.

BAROCLINIC INSTABILITY 5. BEYOND THAT, THE EQUILIBRIUM IS READY TO BREAK DOWN AT THE SLIGHEST PROVOCATION. IN A PERTURBATION SUPERIMPOSED ON THID BASIC STATE, COLD POLAR AIR FLOWS EQUATORWARD AND THE RELATIVELY WARM SUB-TROPICAL AIR FLOWS POLEWARD SO THAT ALONG A LATITUDE CIRCLE, WE HAVE NOW COLD AND WARM AIR SIDE BY SIDE. 6. AZ IS CONVERTED IN TO AE. GENERALLY, A SITUATION PREVAILS IN WHICH WARM AIR RISES AND COLD AIR SINKS IN x-p PLANE. AE IS CONVERTED INTO KE. AZ AE KE 7. THE STORE HOUSE OF AZ IS CONTINUOUSLY FED BY DIFFERENTIAL HEATING OF DIFFERENT LATITUDE ZONES FOR WHICH SOLAR HEATING IS THE ULTIMATE CAUSE. KE IS CONTINUOUSLY DRAINED OUT OF THE SYSTEM BY FRICTION.
c9c3bd51de4f14dfadfee296a3634af2.ppt