d28dbf59cac53190225356d2498c2f56.ppt
- Количество слайдов: 53

Bandera Tool Set Presented by: Dor Nir

Outline n n n n Specification Language (LTL) Software verification problems Introduction to Bandera tool Set Bandera Specification Language (BSL) Data Type Abstraction Slicing Results and conclusions
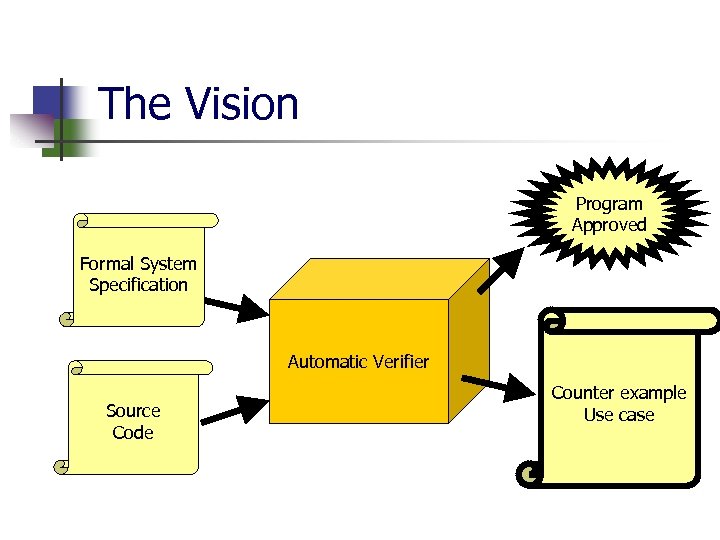
The Vision Program Approved Formal System Requirements Specification Automatic Verifier Source Code Counter example Use case

Specification Languages n n n Linear Temporal Logic (LTL) Computation Tree Logic (CTL, CTL*) Excplicit Clock Temporal Logic (XCTL) Temporal Logic of Actions (TLA, TLA+) Interval Temporal Logic (ITL)
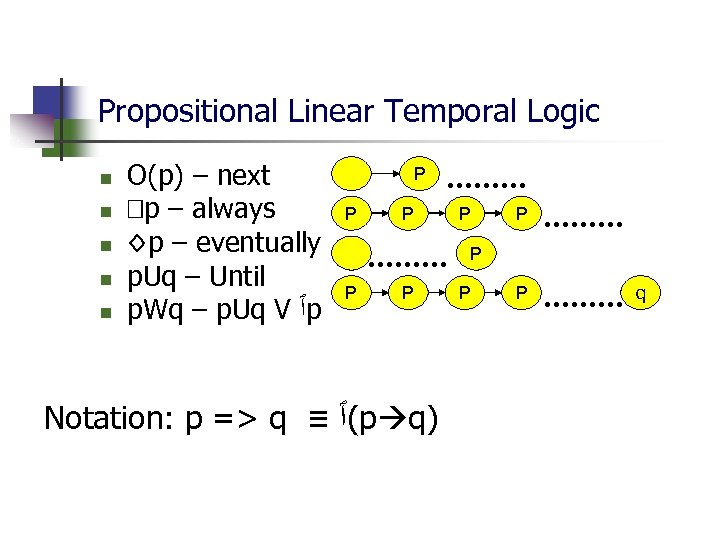
Propositional Linear Temporal Logic n n n O(p) – next p – always ◊p – eventually p. Uq – Until p. Wq – p. Uq V ٱ p P P P P Notation: p => q ≡ (ٱ p q) P P q

Some typical property patterns Recurrence n ◊p infinitely often n ◊ p eventually always Precendence n p. U(q. Ur) p* q* r n (p. Uq)Ur (p*q)* r n ¬p. Wq p cannot occur before q r P q

Mutual Exclusion Properties • Resource is never owned by P 1 and P 2, simultaneously (P 1_own P 2_own) • Whenever P 1 has requested the resource it will eventually get it (P 1_req P 1_own) • If P 1 requests the resource infinitely often (when the resource is free then it will infinitely often get it (strong fairness) (P 1_req (P 1_own P 2_own)) P 1_own
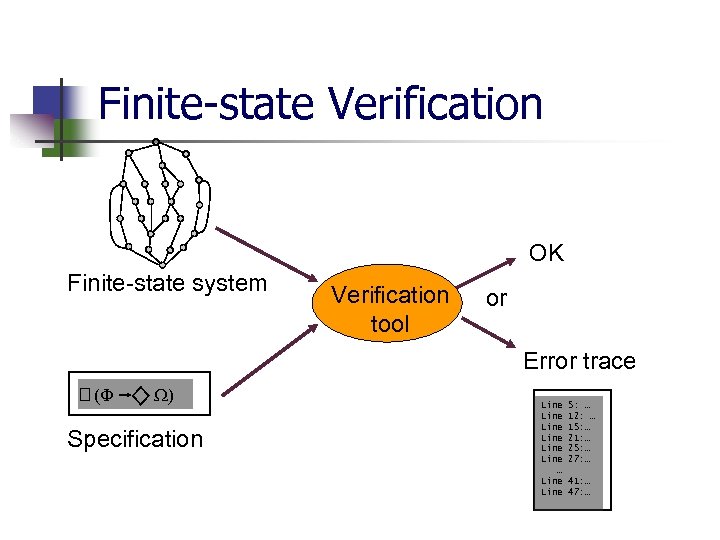
Finite-state Verification OK Finite-state system Verification tool or Error trace (F W) Specification Line Line … Line 5: … 12: … 15: … 21: … 25: … 27: … 41: … 47: …

Finite-state Verification n Widespread success and Effective for analyzing properties of adoption in industry hardware systems

Software verification l Recent years have seen many efforts to apply those techniques to software Limited success due to the enormous state spaces associated with most software systems
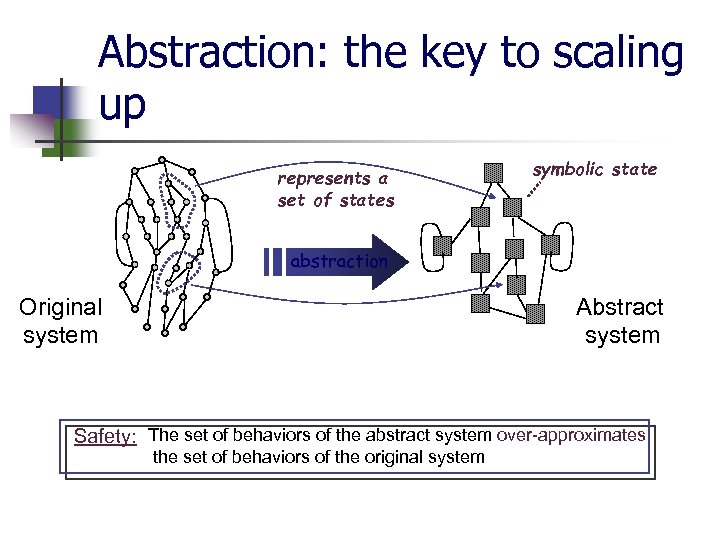
Abstraction: the key to scaling up represents a set of states symbolic state abstraction Original system Abstract system Safety: The set of behaviors of the abstract system over-approximates the set of behaviors of the original system

Goals… • Verification tool for software, using abstraction. • Easy for writing specifications. • Use of existing verification tools. • Verification time is reasonable. • Easy to understand the counter example. • Reusable. (Specifications)
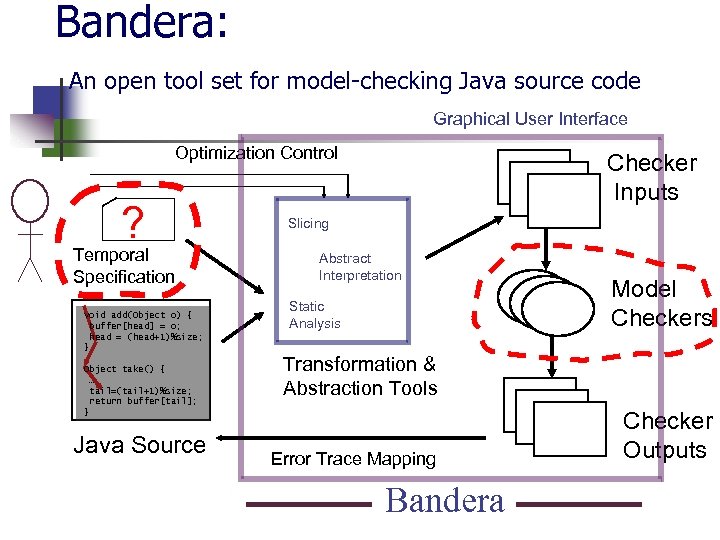
Bandera: An open tool set for model-checking Java source code Graphical User Interface Optimization Control ? Temporal Specification void add(Object o) { buffer[head] = o; head = (head+1)%size; } Object take() { … tail=(tail+1)%size; return buffer[tail]; } Java Source Checker Inputs Slicing Abstract Interpretation Static Analysis Model Checkers Transformation & Abstraction Tools Error Trace Mapping Bandera Checker Outputs

Issue: Rendering Requirement n Often difficult to formalize a requirement in temporal logic “Between the window open and the window close, button X can be pushed at most twice. ” …is rendered in LTL as. . . []((open && <>close) -> ((!push. X && !close) U (close || ((push. X && !close) U (close || (!push. X U close)))))
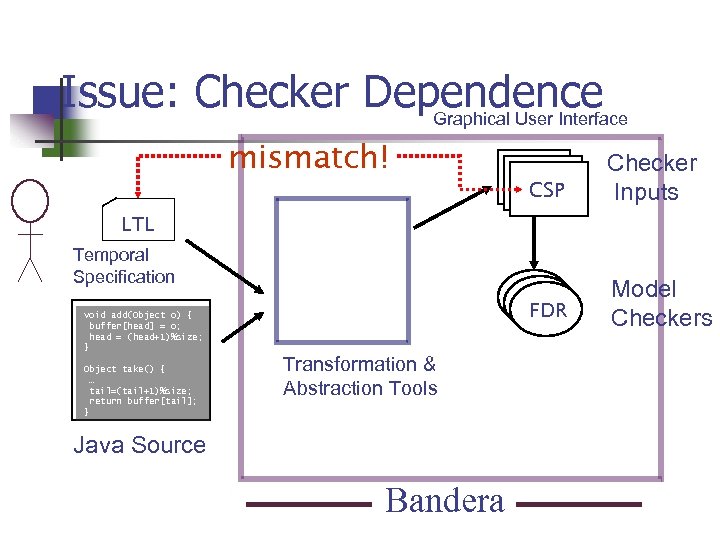
Issue: Checker Dependence Graphical User Interface mismatch! LTL CSP Checker Inputs Spin SMV FDR Model Checkers LTL Temporal Specification void add(Object o) { buffer[head] = o; head = (head+1)%size; } Object take() { … tail=(tail+1)%size; return buffer[tail]; } Transformation & Abstraction Tools Java Source Bandera

Issue: Representation Dependence n Source’s representation Heap. b. head == Heap. b. tail n Model’s representation (((_collect(heap_b) == 1) && (Bounded. Buffer_col. instance[_index(heap _b)]. head == Bounded. Buffer_col. instance[_index(heap _b)]. tail) ) || ((_collect(heap _b) == 3) && (Bounded. Buffer_col_0. instance[_index(heap _b)]. head == Bounded. Buffer_col_0. instance[_index(heap _b)]. tail) ) || ((_collect(heap _b) == 0) && TRAP))

Problem summary n n Rendering Checker dependence Representation dependence Quantification

BSL: Bandera Specification Language n n n Propositions stated in terms of source code features Based on an extensible system of temporal specification patterns Heap objects are named via object quantification Quantification Temporal Property Specification (via pattern language) Assertion Property Specification (selective enabling) Predicate Definition Assertion Definition
![Predicate Forms n Static/Instance Data Constraints @observable [static] EXP <name> <exp>; n Invocation @observable Predicate Forms n Static/Instance Data Constraints @observable [static] EXP <name> <exp>; n Invocation @observable](https://present5.com/presentation/d28dbf59cac53190225356d2498c2f56/image-19.jpg)
Predicate Forms n Static/Instance Data Constraints @observable [static] EXP <name> <exp>; n Invocation @observable INVOKE <name> <exp>; n Return @observable RETURN <name> <exp>; n Arbitrary Locations @observable LOCATION[<label>] <name> <exp>;

Semantic Issues (o 1 != null) && (o 1. next != null) && ( o 1. next. value == 0 )
![Quantification (Cont’d) forall[b: Bounded. Buffer]. {Full(b)} leads to {!Full(b)} globally; (heap. b == null Quantification (Cont’d) forall[b: Bounded. Buffer]. {Full(b)} leads to {!Full(b)} globally; (heap. b == null](https://present5.com/presentation/d28dbf59cac53190225356d2498c2f56/image-21.jpg)
Quantification (Cont’d) forall[b: Bounded. Buffer]. {Full(b)} leads to {!Full(b)} globally; (heap. b == null U (heap. b != null && ([](heap. b. head == heap. b. tail) -> <>(heap. b. head != heap. b. tail)))) || [](heap. b == null)

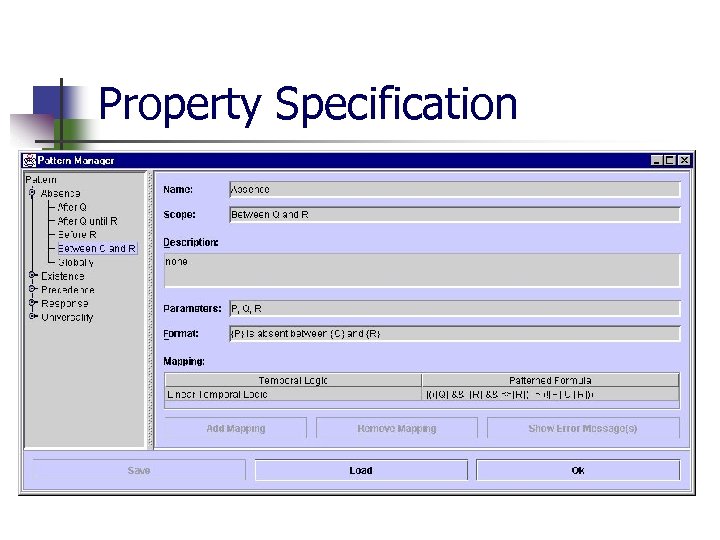
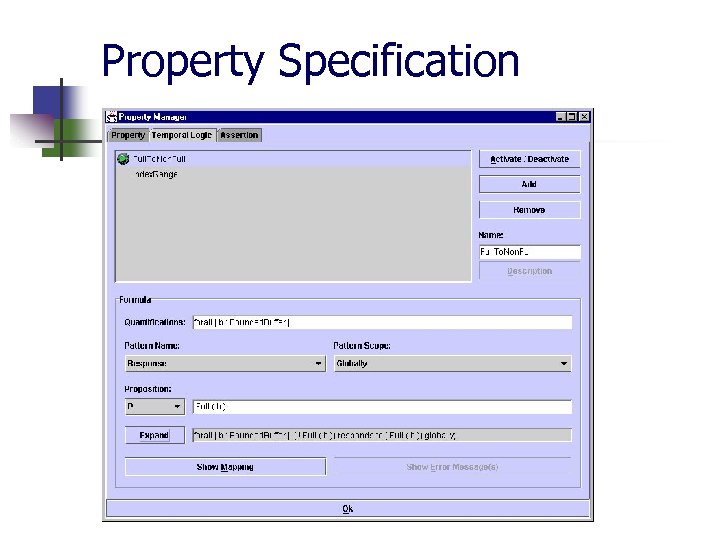
Methodology: Property Specification Given a software requirement. . . n Identify observables (propositions) in requirement n Define propositions in source Java-doc comments n Use GUI to select appropriate temporal pattern parameterized by declared observables n Add quantification if property contains instance propositions.
![Bounded Buffer class Bounded. Buffer { Object [] buffer; int head; /* next available Bounded Buffer class Bounded. Buffer { Object [] buffer; int head; /* next available](https://present5.com/presentation/d28dbf59cac53190225356d2498c2f56/image-23.jpg)
Bounded Buffer class Bounded. Buffer { Object [] buffer; int head; /* next available slot */ int tail; /* last available slot */ int bound; /* max # of elements */ Initialization head tail Add, Add public Bounded. Buffer(int b) {…} head tail public synchronized boolean is. Empty() {…} public synchronized void add(Object o) {…} public synchronized Object take () {…} } Add, Take tail head

Bounded Buffer Initialization public Bounded. Buffer(int b) { bound = b; buffer = new Object[bound]; head = 0; tail = bound-1; } public synchronized boolean is. Empty() { return head == ((tail+1) % bound); } head tail Add, Add head tail Add, Take tail head
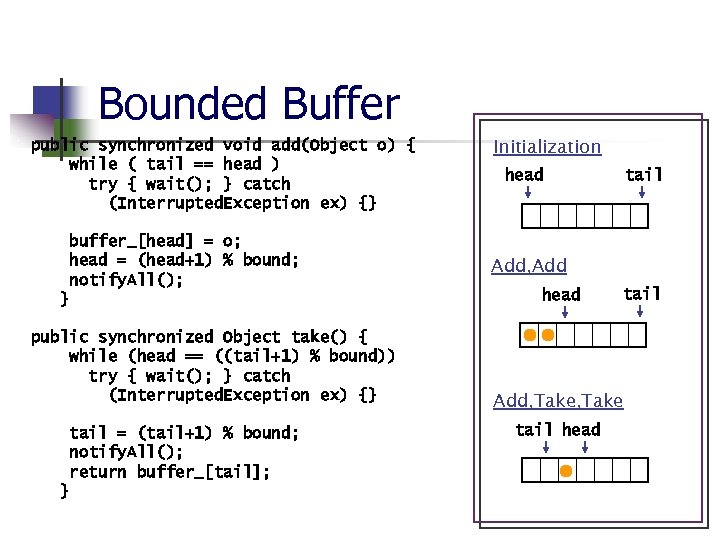
Bounded Buffer public synchronized void add(Object o) { while ( tail == head ) try { wait(); } catch (Interrupted. Exception ex) {} buffer_[head] = o; head = (head+1) % bound; notify. All(); } public synchronized Object take() { while (head == ((tail+1) % bound)) try { wait(); } catch (Interrupted. Exception ex) {} tail = (tail+1) % bound; notify. All(); return buffer_[tail]; } Initialization head tail Add, Add head tail Add, Take tail head

Bounded Buffer Properties n n Full buffers eventually become non -full Indices always stay in range Empty buffers must be added to before being taken from Buffers are constructed with positive bounds

Property Specification /** * @observable * EXP Full: (head == tail); */ class Bounded. Buffer { Object [] buffer; int head, tail, bound; public synchronized void add(Object o) {…} public synchronized Object take () {…} } Requirement 1: If a buffer becomes full, it will eventually become non-full. Bandera Specification: Full. To. Non. Full: forall[b: Bounded. Buffer]. {!Full(b)} responds to {Full(b)} globally;

Property Specification /** * @observable * EXP Head. Range: * head >= 0 && head < bound; * Exp Tail. Range: * tail >= 0 && tail < bound; */ Requirement 2: Indices always stay in range. class Bounded. Buffer { Object [] buffer; int head, tail, bound; public synchronized void add(Object o) {…} public synchronized Object take () {…} } Bandera Specification: Index. Range. Invariant: forall[b: Bounded. Buffer]. {Head. Range(b) && Tail. Range(b)} is universal globally;

Property Specification /** * @observable * EXP Empty: * head == ((tail+1) % bound); */ class Bounded. Buffer { int head, tail, bound; /** * @observable INVOKE Call; */ public synchronized void add(Object o) {…} /** * @observable RETURN Return; */ public synchronized Object take () {…} } Requirement 3: Empty buffers must added to before being taken from Bandera Specification: No. Take. While. Empty: forall[b: Bounded. Buffer]. {take. Return(b)} is absent after {Empty(b)} until {add. Call(b)};

Property Specification /** * @assert * PRE Positive. Bound: * (b > 0); */ public Bounded. Buffer(int b) { bound = b; buffer = new Object[bound]; head = 0; tail = bound-1; } Requirement 4: Buffers are constructed with positive bounds Bandera Specification: Positive. Bound: enable assertions {Positive. Bound};
![Quantification n forall[b: Bounded. Buffer]. P(b) Quantified set is not fixed n n n Quantification n forall[b: Bounded. Buffer]. P(b) Quantified set is not fixed n n n](https://present5.com/presentation/d28dbf59cac53190225356d2498c2f56/image-31.jpg)
Quantification n forall[b: Bounded. Buffer]. P(b) Quantified set is not fixed n n n varies within executions varies across executions Solution n n by adding a state variable (for b) that will eventually be bound nondeterministically to each instance by enabling checking of the formula only when variable is bound to an instance
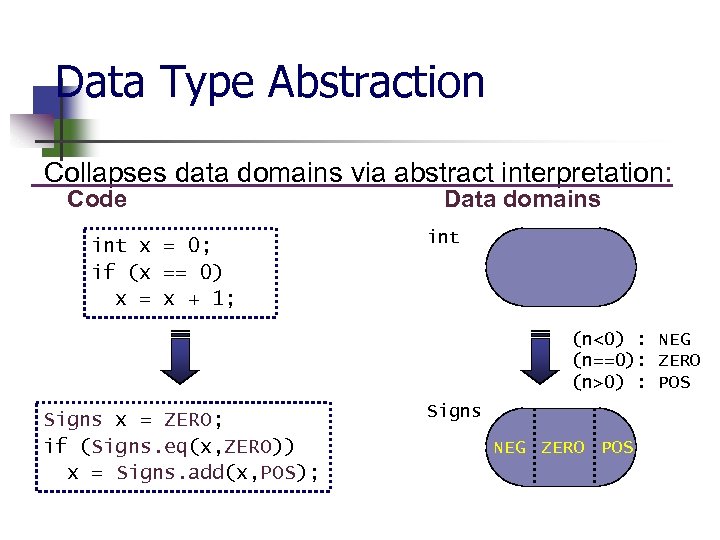
Data Type Abstraction Collapses data domains via abstract interpretation: Code int x = 0; if (x == 0) x = x + 1; Data domains int (n<0) : NEG (n==0): ZERO (n>0) : POS Signs x = ZERO; if (Signs. eq(x, ZERO)) x = Signs. add(x, POS); Signs NEG ZERO POS

Bandera hypothesis Abstraction of data domains is necessary Automated support for n n Defining abstract domains (and operators) Selecting abstractions for program components Generating abstract program models Interpreting abstract counter-examples will make it possible to n n Scale property verification to realistic systems Ensure the safety of the verification process
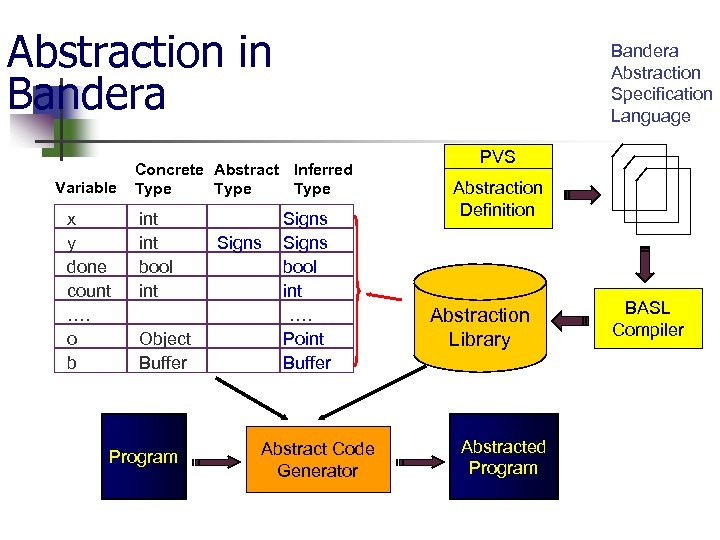
Abstraction in Bandera Variable x y done count …. o b Bandera Abstraction Specification Language Concrete Abstract Inferred Type int bool int Object Buffer Program Signs bool int …. Point Buffer Abstract Code Generator PVS Abstraction Definition Abstraction Library Abstracted Program BASL Compiler

Definition of Abstractions in BASL abstraction Signs abstracts int begin TOKENS = { NEG, ZERO, POS }; abstract(n) begin n < 0 n == 0 n > 0 end -> {NEG}; -> {ZERO}; -> {POS}; Automatic Generation operator + add begin (NEG , NEG) -> {NEG} ; (NEG , ZERO) -> {NEG} ; (ZERO, NEG) -> {NEG} ; (ZERO, ZERO) -> {ZERO} ; (ZERO, POS) -> {POS} ; (POS , ZERO) -> {POS} ; (POS , POS) -> {POS} ; (_, _) -> {NEG, ZERO, POS}; /* case (POS, NEG), (NEG, POS) */ end Example: Start safe, then refine: +(NEG, NEG)={NEG, ZERO, POS} Proof obligations submitted to PVS. . . Forall n 1, n 2: neg? (n 1) and neg? (n 2) implies not pos? (n 1+n 2) Forall n 1, n 2: neg? (n 1) and neg? (n 2) implies not zero? (n 1+n 2) Forall n 1, n 2: neg? (n 1) and neg? (n 2) implies not neg? (n 1+n 2)

Compiling BASL Definitions abstraction Signs abstracts int begin TOKENS = { NEG, ZERO, POS }; abstract(n) begin n < 0 n == 0 n > 0 end public class Signs { public static final int NEG = 0; // mask 1 public static final int ZERO = 1; // mask 2 public static final int POS = 2; // mask 4 -> {NEG}; -> {ZERO}; -> {POS}; Compiled operator + add begin (NEG , NEG) -> {NEG} ; (NEG , ZERO) -> {NEG} ; (ZERO, NEG) -> {NEG} ; (ZERO, ZERO) -> {ZERO} ; (ZERO, POS) -> {POS} ; (POS , ZERO) -> {POS} ; (POS , POS) -> {POS} ; (_, _)-> {NEG, ZERO, POS}; /* case (POS, NEG), (NEG, POS) */ end public static int abs(int n) { if (n < 0) return NEG; if (n == 0) return ZERO; if (n > 0) return POS; } public static int add(int arg 1, int arg 2) { if (arg 1==NEG && arg 2==NEG) return NEG; if (arg 1==NEG && arg 2==ZERO) return NEG; if (arg 1==ZERO && arg 2==NEG) return NEG; if (arg 1==ZERO && arg 2==ZERO) return ZERO; if (arg 1==ZERO && arg 2==POS) return POS; if (arg 1==POS && arg 2==ZERO) return POS; if (arg 1==POS && arg 2==POS) return POS; return Bandera. choose(7); /* case (POS, NEG), (NEG, POS) */ }

Data Type Abstractions n Library of abstractions for base types contains: n Range(i, j), i. . j modeled precisely, e. g. , Range(0, 0) is the signs abstraction n Modulo(k), Set(v, …) n Point maps all concrete values to unknown n User extendable for base types n Array abstractions n Specified by an index abstraction and an element abstraction n Class abstractions n Specified by abstractions for each field

Interpreting Results l For an abstracted program, a counter-example may be infeasible because: – Over-approximation introduced by abstraction n Example: x = -2; if(x + 2 == 0) then. . . x = NEG; if(Signs. eq(Signs. add(x, POS), ZERO)) then. . . {NEG, ZERO, POS}

Slicing Generate reduced model n Program P with specification Φ n Bandera collect statements of interest From Φ (slicing criterion for Φ) n Compute P’: reduce version of P. n P |= Φ P’|= Φ n
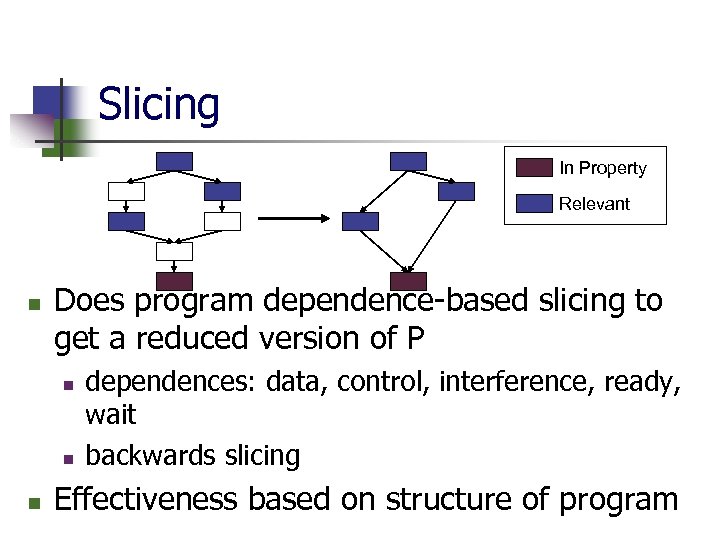
Slicing In Property Relevant n Does program dependence-based slicing to get a reduced version of P n n n dependences: data, control, interference, ready, wait backwards slicing Effectiveness based on structure of program

Counter-Example: Overview Counter-example with a thousand states? !? ! Bandera provides debugger-like features: n n n n map states to source code program tracing create checkpoints keep track of variables and objects UML-like object displays lock graphs
Using Bandera • Launch the Bandera User Interface (BUI) from the command line • Future runs: save which components you want to use in session files
Counter-Example: Program Tracing
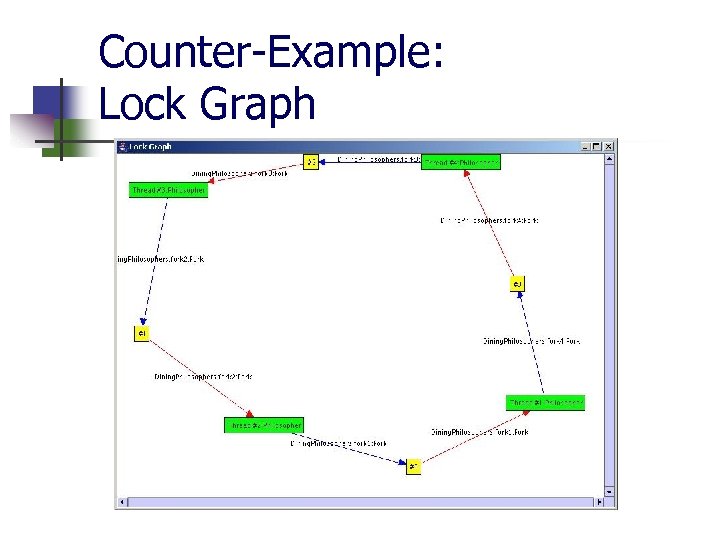
Counter-Example: Lock Graph

Counter-Example: Object Viewer
Property Specification
Property Specification
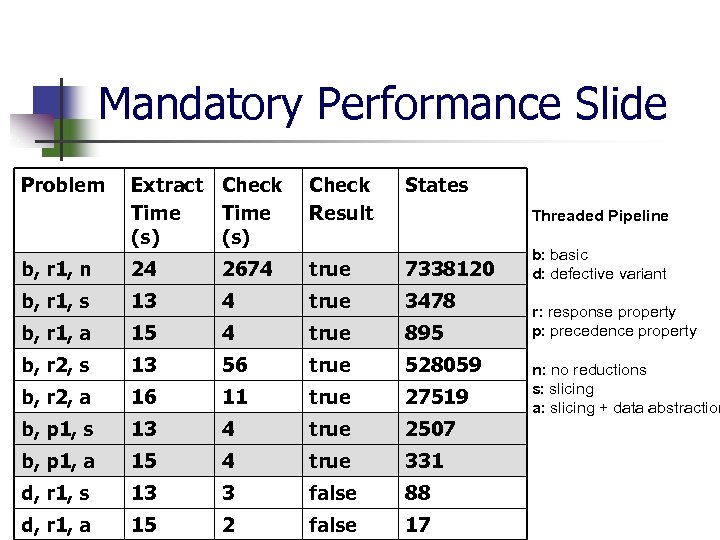
Mandatory Performance Slide Problem Extract Check Time (s) Check Result States b, r 1, n 24 2674 true 7338120 b, r 1, s 13 4 true 3478 b, r 1, a 15 4 true 895 b, r 2, s 13 56 true 528059 b, r 2, a 16 11 true 27519 b, p 1, s 13 4 true 2507 b, p 1, a 15 4 true 331 d, r 1, s 13 3 false 88 d, r 1, a 15 2 false 17 Threaded Pipeline b: basic d: defective variant r: response property p: precedence property n: no reductions s: slicing a: slicing + data abstraction
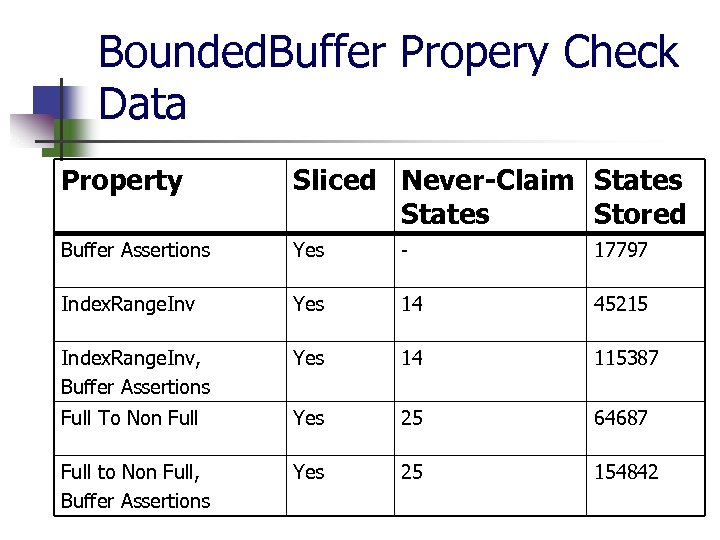
Bounded. Buffer Propery Check Data Property Sliced Never-Claim States Stored Buffer Assertions Yes - 17797 Index. Range. Inv Yes 14 45215 Index. Range. Inv, Buffer Assertions Yes 14 115387 Full To Non Full Yes 25 64687 Full to Non Full, Buffer Assertions Yes 25 154842

When to Use Model Checking n Control-related properties n n Container objects n n n assertions pre- and post-conditions simple data invariants Stacks Queues Verifying concurrent behavior Necessity for counter-examples Automatic property verification of source code

Analysis Not Appropriate for Model Checking n Data-related properties n n n Verification of sorting algorithms Use other formal methods instead (theorem proving) Where static dataflow analysis is better n n n array-bounds errors buffer overruns null-pointer de-referencing

Conclusions n n Software verification is applicable and can help. (but…) Slicing is critical. BSL making the specification writing much more simple. (but…) The counter example is intuitive.

Future work n n n More quantifications (array) Support predicate with arbitrary parameters Method invocation in predicate. More model checkers. Increase the template library
d28dbf59cac53190225356d2498c2f56.ppt