bb1a63410c114df035deb2292dd1a05a.ppt
- Количество слайдов: 52

“Backward” Particle Detection for 12 Ge. V in Hall C Meeting, January 18 -19, 2008 Jefferson Lab, Newport News, VA USA Eli Piasetzky Tel Aviv University, ISRAEL
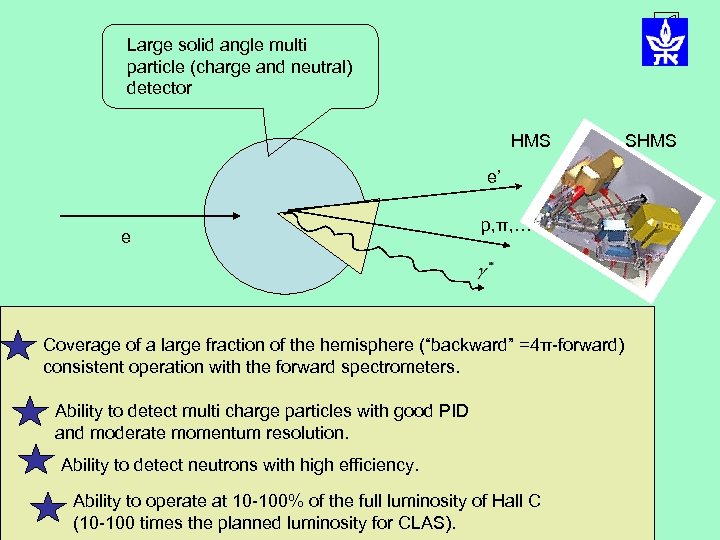
Large solid angle multi particle (charge and neutral) detector HMS SHMS e’ e p, π, … Coverage of a large fraction of the hemisphere (“backward” =4π-forward) consistent operation with the forward spectrometers. Ability to detect multi charge particles with good PID and moderate momentum resolution. Ability to detect neutrons with high efficiency. Ability to operate at 10 -100% of the full luminosity of Hall C (10 -100 times the planned luminosity for CLAS).

The physics driving a “ 4π-forward” detector Short Range Correlations (SRC) EMC Hadronization Study of GPDs Nuclear Matter in non - equilibrium condition
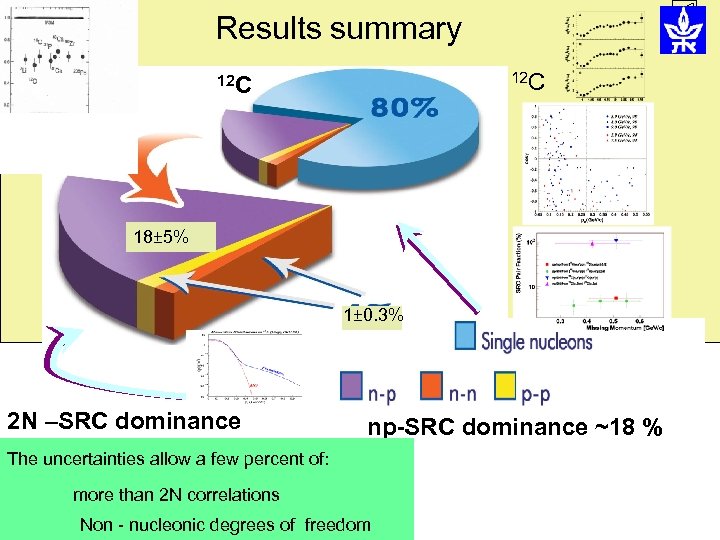
Results summary 12 C 18± 5% 1± 0. 3% 2 N –SRC dominance np-SRC dominance ~18 % The uncertainties allow a few percent of: more than 2 N correlations Non - nucleonic degrees of freedom
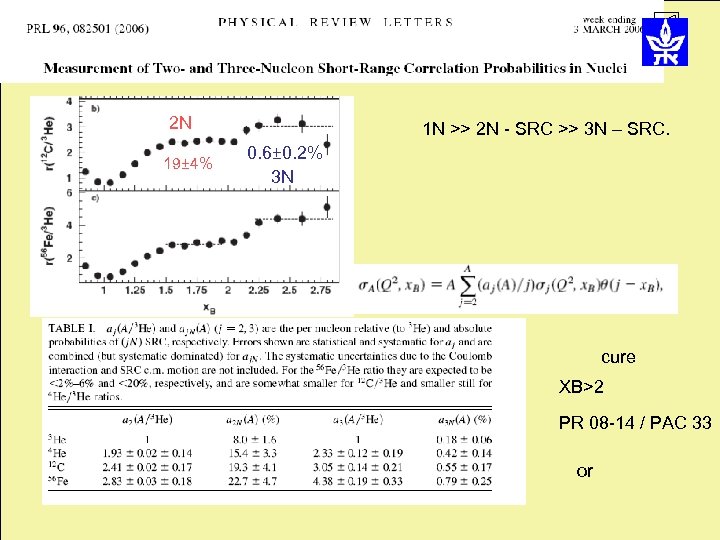
2 N 19± 4% 1 N >> 2 N - SRC >> 3 N – SRC. 0. 6± 0. 2% 3 N cure XB>2 PR 08 -14 / PAC 33 or
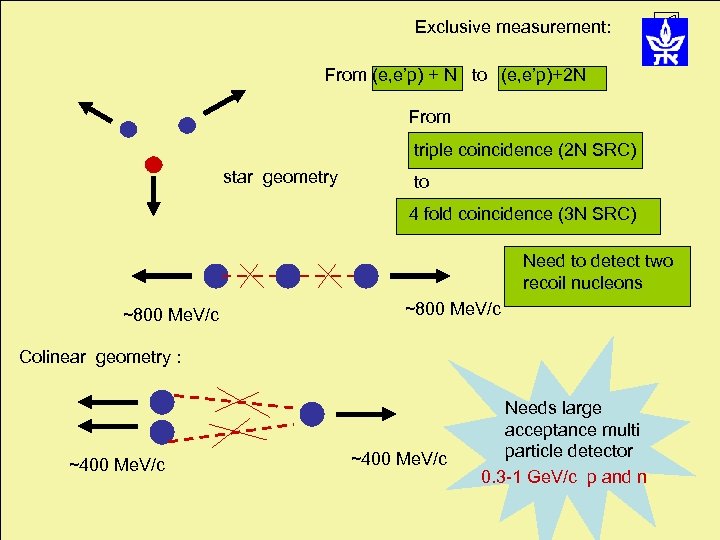
Exclusive measurement: From (e, e’p) + N to (e, e’p)+2 N From triple coincidence (2 N SRC) star geometry to 4 fold coincidence (3 N SRC) Need to detect two recoil nucleons ~800 Me. V/c Colinear geometry : ~400 Me. V/c Needs large acceptance multi particle detector 0. 3 -1 Ge. V/c p and n
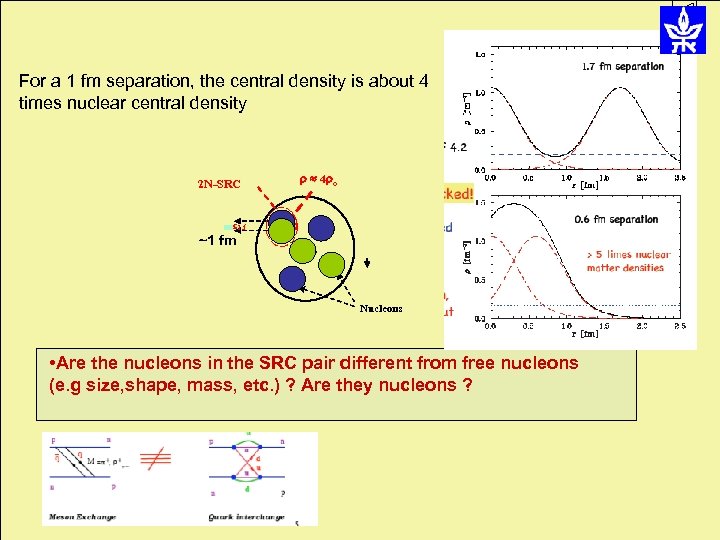
For a 1 fm separation, the central density is about 4 times nuclear central density 2 N-SRC 4 o 1. f ~1 fm Nucleons • Are the nucleons in the SRC pair different from free nucleons (e. g size, shape, mass, etc. ) ? Are they nucleons ?

Looking for non-nucleonic degrees of freedom 2 N-SRC 5 o 1. f Breaking the pair will yield more backward Δ, π , k ~1 fm Nucleons The signature of a non-nucleonic SRC intermediate state is a large branching ratio to a non-nucleonic final state.

Looking for non-nucleonic degrees of freedom Expected Δ’s rates 5 -10% of recoil N Detected by spectrometer 4 fold coincidence 2 particles in the backward detector 3 -5 fold coincidence 2 -4 particles in the backward detector

Title: Search for cumulative Delta 0 (1232) and (1232) isobars in neutrino interactions with neon nuclei + + Authors: Ammosov, V. V. ; Asratyan, A. É. ; Burtovoǐ, V. S. ; Gapienko, V. A. ; Gapienko, G. S. ; Gorichev, P. A. ; Denisov, A. G. ; Zaets, V. G. ; Klyukhin, V. I. ; Koreshev, V. I. ; Kruchinin, S. P. ; Kubantsev, M. A. ; Makhlyueva, I. V. ; Pitukhin, P. V. ; Sirotenko, V. I. ; Slobodyuk, E. A. ; Usubov, Z. U. ; Fedotov, A. V. ; Shevchenko, V. G. ; Shekelyan, V. I. Publicati on: Journal of Experimental and Theoretical Physics Letters, Vol. 40, p. 1041 Publicati on Date: 09/1984
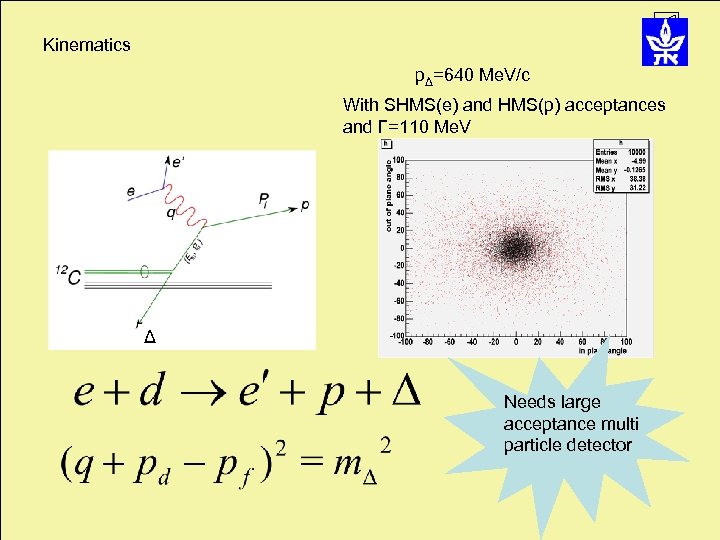
Kinematics pΔ=640 Me. V/c With SHMS(e) and HMS(p) acceptances and Γ=110 Me. V Δ Needs large acceptance multi particle detector
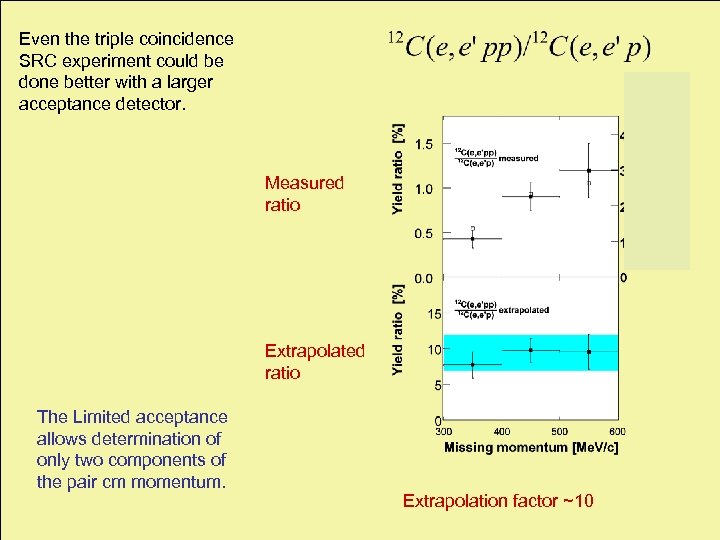
Even the triple coincidence SRC experiment could be done better with a larger acceptance detector. Measured ratio Extrapolated ratio The Limited acceptance allows determination of only two components of the pair cm momentum. Extrapolation factor ~10

EMC A large acceptance detector allows tagging of the DIS event High nuclear density tagging : A recoil high momentum nucleon to the backward hemisphere is a signature of 2 N-SRC i. e large local nuclear density. Due to the dominance of np-SRC pairs: a recoil neutron tags a proton structure function a recoil proton tags a neutron structure function Flavor tagging : Identifying a π + or π - with a large z can point to the flavor of the struck quark ( u or d). Recoil and forward tagging allows the study of u, d in p, n

Hadronization Measure the multiplicity and the type of emitted particles in a large acceptance “backward direction ” in coincidence with the forward (large z) leading π +, π -, k +, k - particle. Difference in hadronization of different quarks Difference between hardonization in a free space and nuclear medium

GPDs Hall B Hall C With a large acceptance detector: With Deuteron one can measure imultaneously both proton and neutron by detecting the recoil neutron or proton respectively ? low mass πN system- a test of chiral symmetry
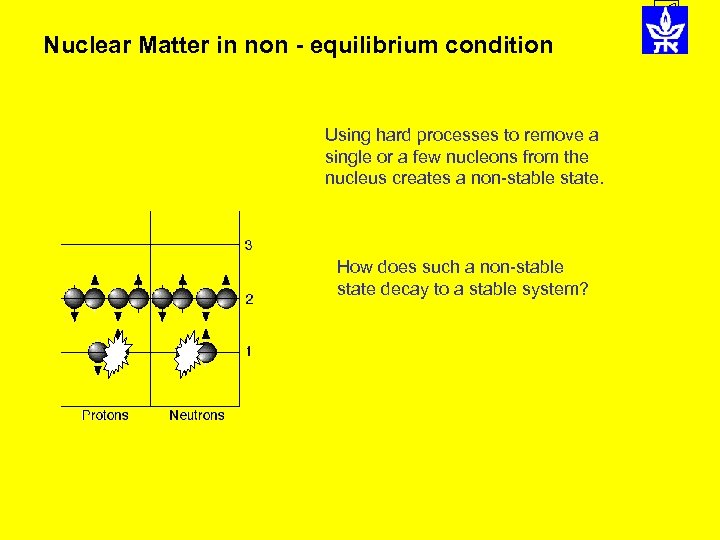
Nuclear Matter in non - equilibrium condition Using hard processes to remove a single or a few nucleons from the nucleus creates a non-stable state. How does such a non-stable state decay to a stable system?

A (4π – forward) DETECTOR Multi particle detection Particle ID Large solid angle- 4π – non-symmetric opening in the forward hemisphere Cover up to ~1800 (the planed 12 Ge. V CLAS cover up to 1350 only) Large (full) luminosity p e’ e Δ Can operate in coincidence with small solid angle, high resolution spectrometer / spectrometers p
G 0 BONUS TPC
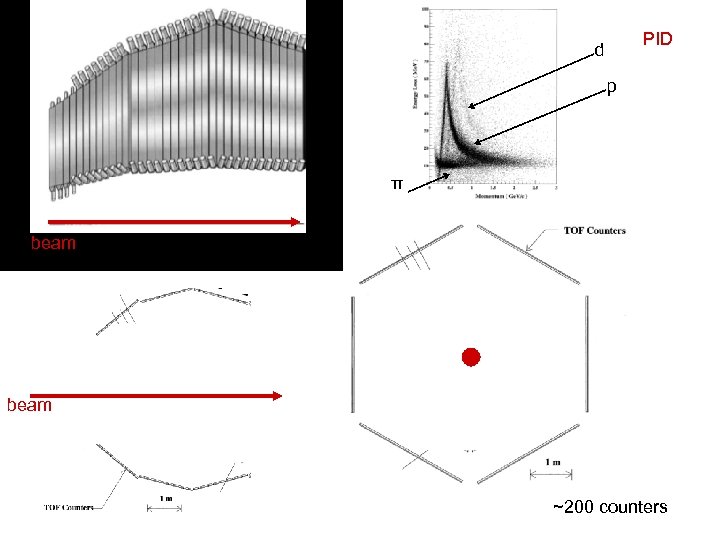
PID d p π beam ~200 counters
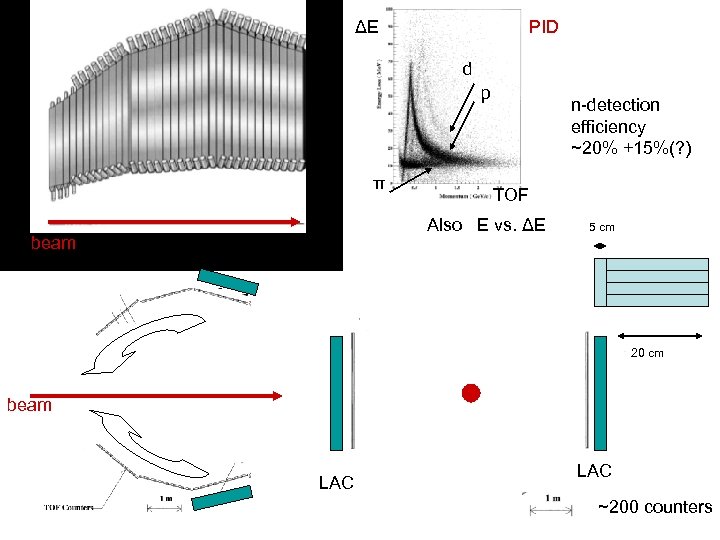
ΔE PID d p π n-detection efficiency ~20% +15%(? ) TOF Also E vs. ΔE beam 5 cm 20 cm beam LAC ~200 counters
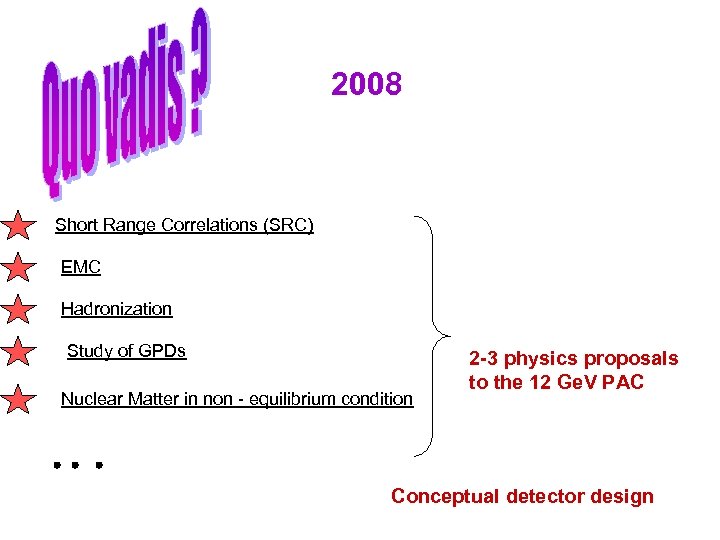
2008 Short Range Correlations (SRC) EMC Hadronization Study of GPDs Nuclear Matter in non - equilibrium condition 2 -3 physics proposals to the 12 Ge. V PAC Conceptual detector design

Acknowledgment Discussions and ideas exchange with: Stepanyan Sebastian Kuhn Larry Weinstein Steve Wood Rolf Ent
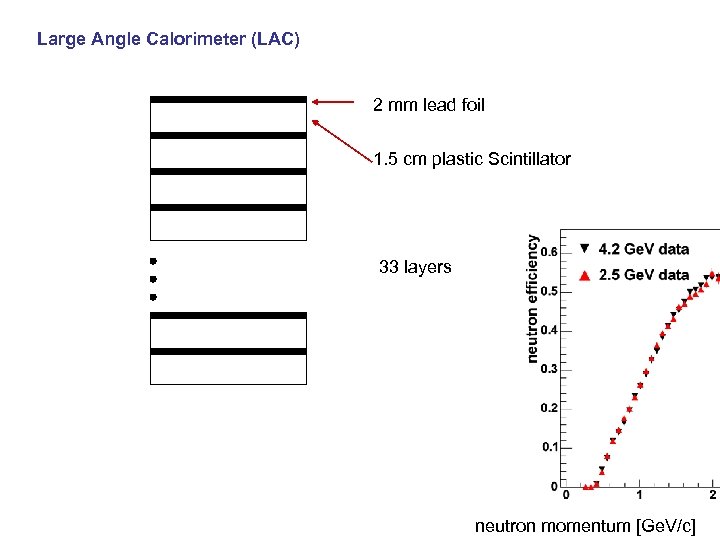
Large Angle Calorimeter (LAC) 2 mm lead foil 1. 5 cm plastic Scintillator 33 layers neutron momentum [Ge. V/c]
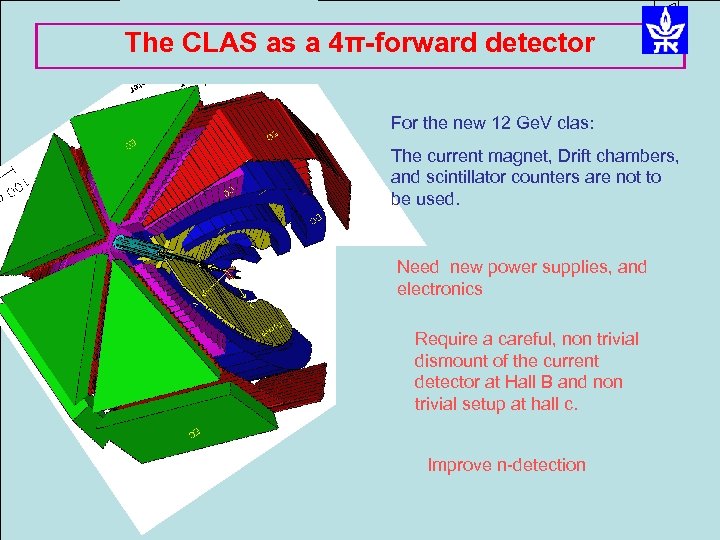
The CLAS as a 4π-forward detector For the new 12 Ge. V clas: The current magnet, Drift chambers, and scintillator counters are not to be used. Need new power supplies, and electronics Require a careful, non trivial dismount of the current detector at Hall B and non trivial setup at hall c. Improve n-detection
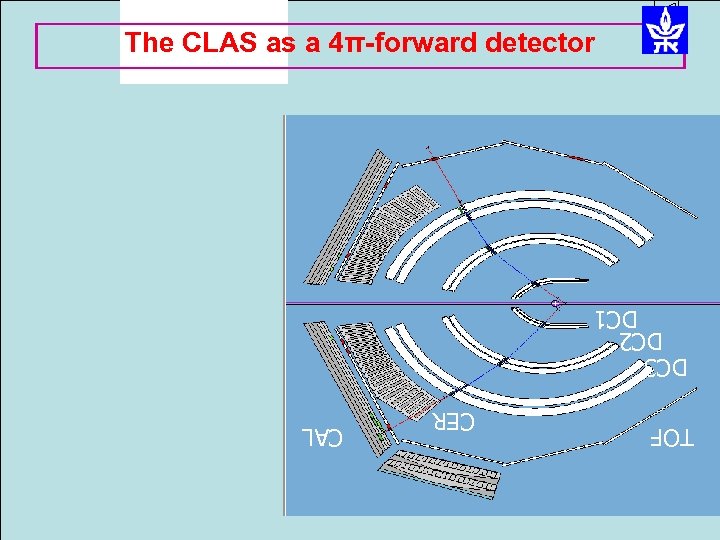
The CLAS as a 4π-forward detector DC 3 DC 2 DC 1 TOF CER CAL
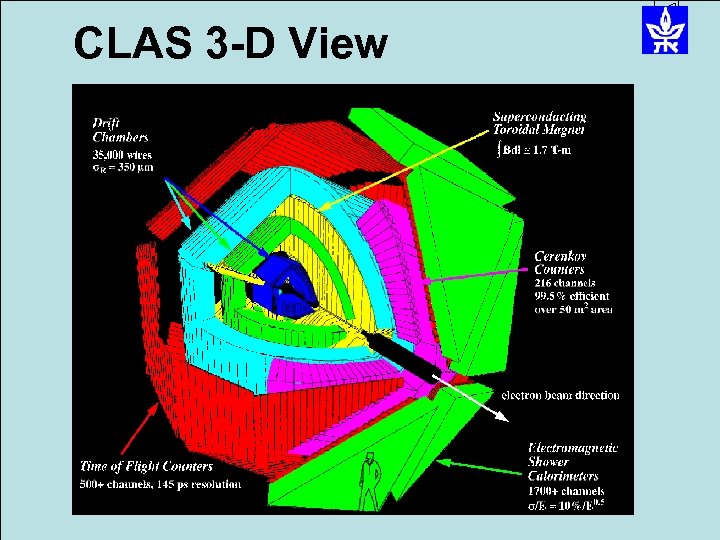
CLAS 3 -D View
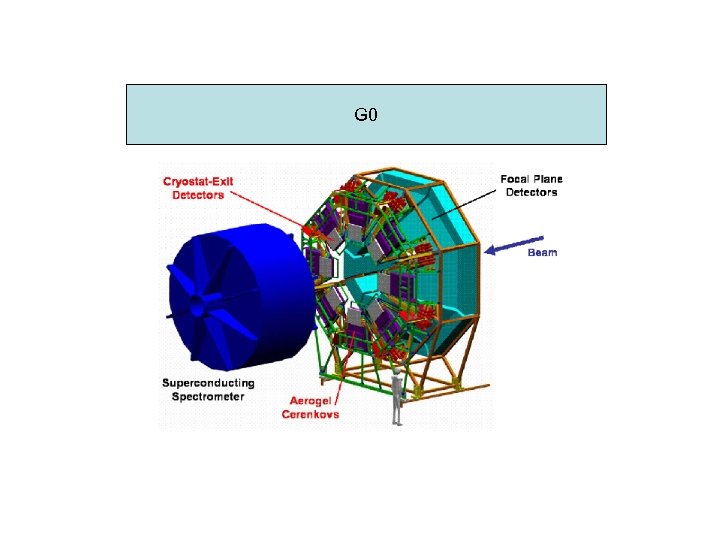
G 0

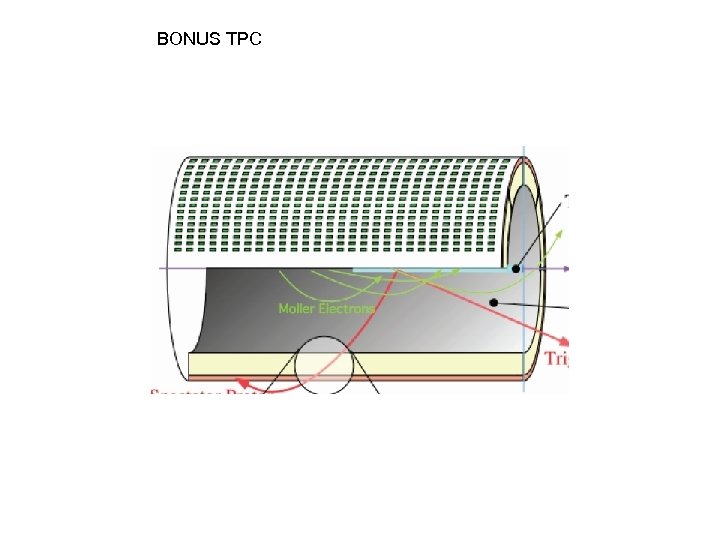
BONUS TPC

SRC in nuclei Roadmap What is the role played by short range correlation of more than two nucleons ? 2 N-SRC How to relate what we learned about SRC in nuclei to the dynamics of neutron star formation and structure ? 5 o SRC 1. f ~1 fm o = 0. 16 Ge. V/fm 3 1. 7 fm 1. 7 f in nuclei Nucleons • Are the nucleons in the SRC pair different from free nucleons (e. g size, shape, mass, etc. ) ? Are they nucleons ? NN interaction: what is the role played by the repulsive core ?
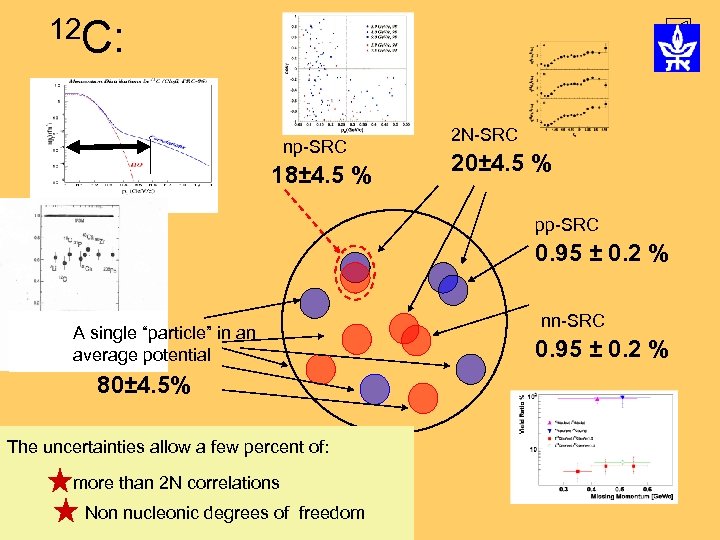
12 C: np-SRC 18± 4. 5 % 2 N-SRC 20± 4. 5 % pp-SRC 0. 95 ± 0. 2 % A single “particle” in an average potential 80± 4. 5% The uncertainties allow a few percent of: more than 2 N correlations Non nucleonic degrees of freedom nn-SRC 0. 95 ± 0. 2 %

Identifying Future Experiments Looking for SRC with more than 2 nucleons:
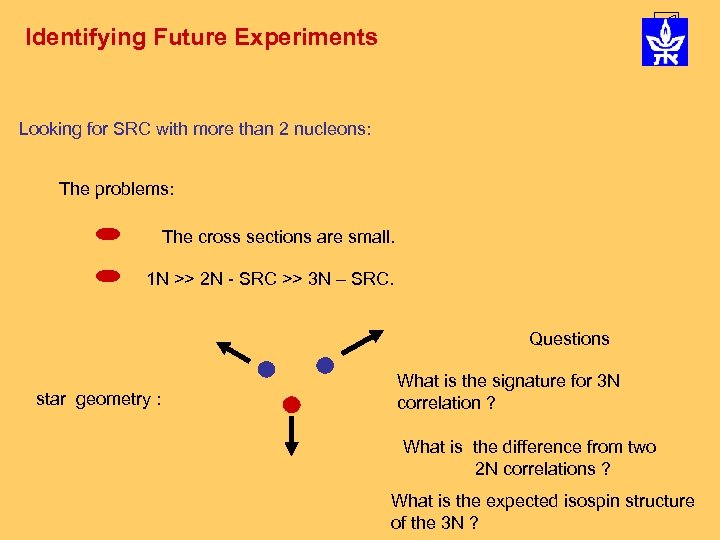
Identifying Future Experiments Looking for SRC with more than 2 nucleons: The problems: The cross sections are small. 1 N >> 2 N - SRC >> 3 N – SRC. Questions star geometry : What is the signature for 3 N correlation ? What is the difference from two 2 N correlations ? What is the expected isospin structure of the 3 N ?

Identifying Future Experiments Looking for SRC with more than 2 nucleons: The problems: The cross sections are small. 1 N >> 2 N - SRC >> 3 N – SRC. The cure for 1 N background is : large pmiss and/or large XB The cure for 2 N-SRC: XB>2 or suppression of the 2 N-SRC at prel=300 -600 Me. V/c for nn or pp pairs.

Identifying Future Experiments Looking for SRC with more than 2 nucleons: Colinear geometry : Initial configurations ~800 Me. V/c ~400 Me. V/c A very strong isospin dependence is expected for the 2 N part. For the 3 N? The 2 N-SRC interaction is suppressed, opening a window of opportunity to identify 3 N correlation. The signal of today is tomorrow’s background
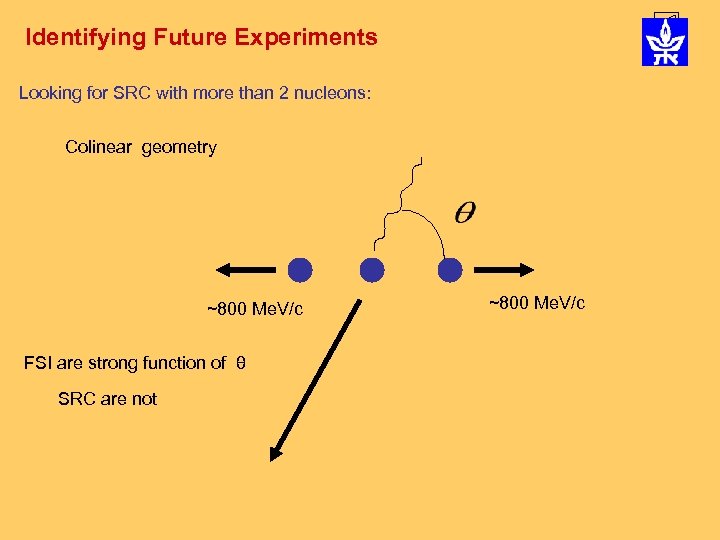
Identifying Future Experiments Looking for SRC with more than 2 nucleons: Colinear geometry ~800 Me. V/c FSI are strong function of θ SRC are not ~800 Me. V/c
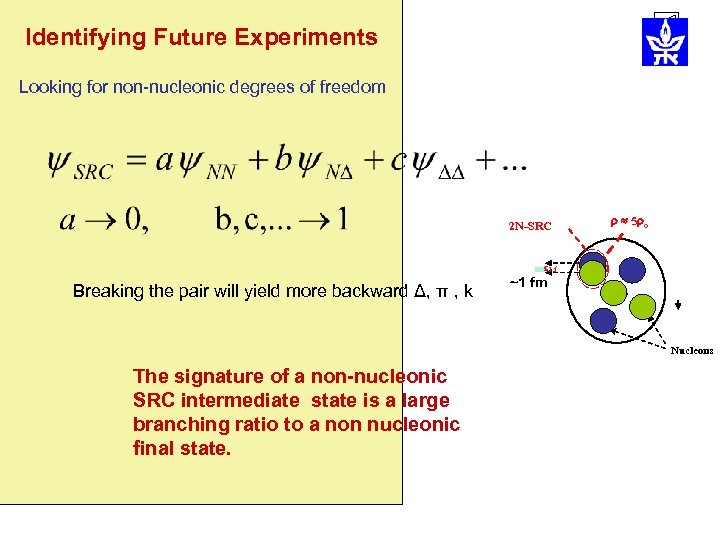
Identifying Future Experiments Looking for non-nucleonic degrees of freedom 2 N-SRC 5 o 1. f Breaking the pair will yield more backward Δ, π , k ~1 fm Nucleons The signature of a non-nucleonic SRC intermediate state is a large branching ratio to a non nucleonic final state.

Looking for non-nucleonic degrees of freedom In coincidence with (e, e’p), as a function of the missing momentum we want to detect; p, n, π-, π+ k - triple coincidence

Identifying Future Experiments Looking for non-nucleonic degrees of freedom “np” pn pΔ 0 p π - p “pp” pp pΔ+ p π+ n 4 fold coincidence Expected rates 5 -10% of recoil N
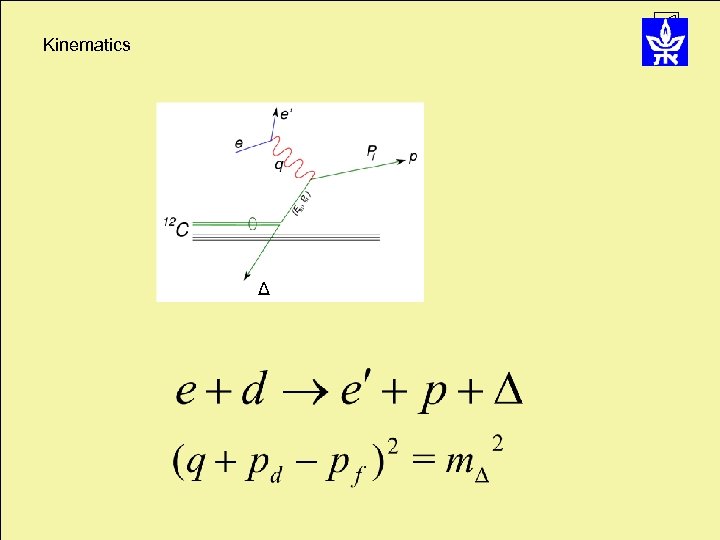
Kinematics Δ
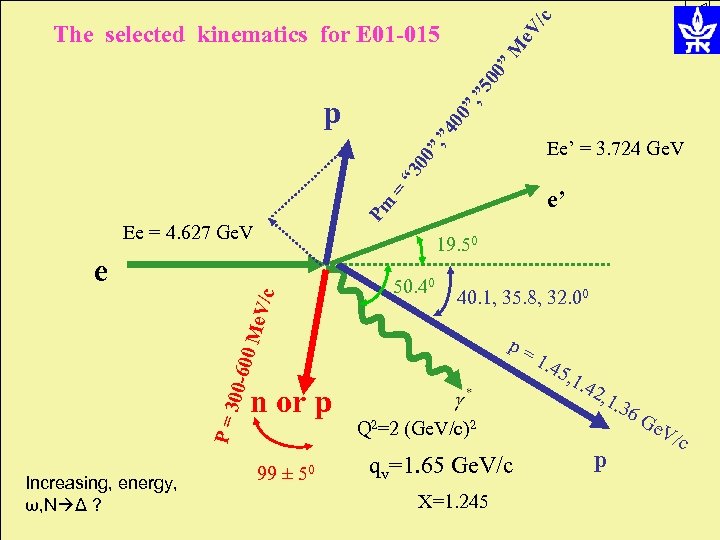
”M e. V /c , ” 5 00 The selected kinematics for E 01 -015 ”, ” 40 0” p “ 3 00 Ee’ = 3. 724 Ge. V Pm = e’ Ee = 4. 627 Ge. V 19. 50 e 40. 1, 35. 8, 32. 00 00 M e. V/c 50. 40 P=3 00 -6 p= Increasing, energy, ω, N Δ ? n or p 99 ± 50 Q 2=2 (Ge. V/c)2 qv=1. 65 Ge. V/c X=1. 245 1. 4 5, 1. 42 , 1. 36 p Ge V/c
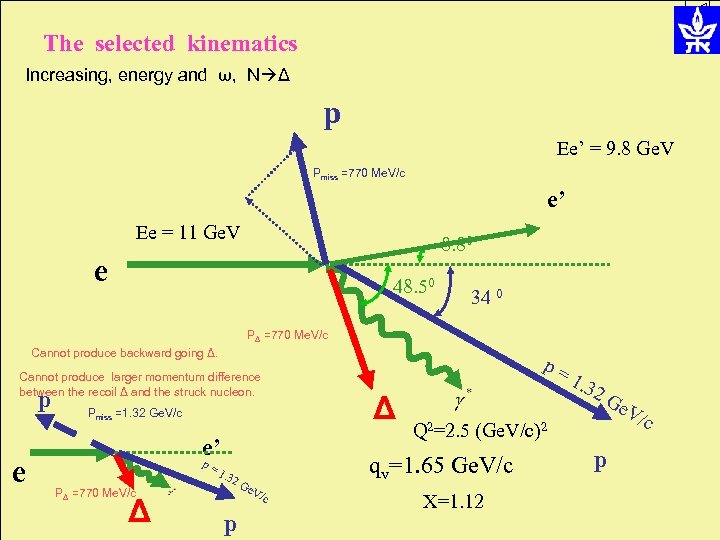
The selected kinematics Increasing, energy and ω, N Δ p Ee’ = 9. 8 Ge. V Pmiss =770 Me. V/c e’ Ee = 11 Ge. V 8. 80 e 48. 50 34 0 PΔ =770 Me. V/c Cannot produce backward going Δ. Cannot produce larger momentum difference between the recoil Δ and the struck nucleon. p e Pmiss =1. 32 Ge. V/c e’ p= PΔ =770 Me. V/c Δ 1. 3 2 G p e. V p= Δ Q 2=2. 5 e. V (Ge. V/c)2 qv=1. 65 Ge. V/c /c 1. 3 2 G X=1. 12 p /c

Ee= 11. 00000 Eout= 9. 790000 theta_e = 8. 800000 Q 2= 2. 535372 x= 1. 116600 input angle of (qe) and (qp) planes 0. 0000000 E+00 theta of q: -48. 49650 The format of the following output is: type of the particle, momentum, angle vs q, angle vs e, azimuthal angle in lab knock-out nucleon 1. 328000 13. 52419 34. 97231 180. 0000 missing 0. 7737520 156. 3361 107. 8397 0. 0000000 E+00 recoil 0. 7737520 23. 66388 72. 16035 180. 0000 tet between recoil and scattred proton -37. 18803 pmiss in the q direction 0. 7086919 Ee= 11. 00000 Eout= 9. 960000 theta_e = 8. 200000 Q 2= 2. 240232 x= 1. 147892 input angle of (qe) and (qp) planes 0. 0000000 E+00 theta of q: -51. 20859 The format of the following output is: type of the particle, momentum, angle vs q, angle vs e, azimuthal angle in lab knock-out nucleon 1. 200000 5. 490372 45. 71821 180. 0000 missing 0. 6385024 169. 6408 118. 4322 0. 0000000 E+00 recoil 0. 6385024 10. 35917 61. 56776 180. 0000 tet between recoil and scattred proton -15. 84955 pmiss in the q direction 0. 6280947

=“ 64 0 M e. V /c The selected kinematics for the measurement Ee’ = 9 Ge. V Pm p Ee = 11 Ge. V e’ 8. 20 e “ 640 Me. V /c 16. 60 Ee= 11. 00000 Eout= 9. 000000 theta_e = 8. 200000 Q 2= 2. 024307 x= 0. 5393709 input angle of (qe) and (qp) planes 0. 0000000 E+00 theta of q: -31. 53330 The format of the following output is: type of the particle, momentum, angle vs q, 0 angle vs e, azimuthal angle in lab knock-out nucleon 2. 300000 14. 94191 16. 59142 179. 9802 missing 0. 6368749 111. 3839 79. 85064 0. 0000000 E+00 recoil 0. 6368749 68. 61605 100. 1494 180. 0000 tet between recoil and scattred proton -83. 55794 pmiss in the q direction 0. 2322146 PΔ = p= 31. 50 Δ 100 Q 2=2 (Ge. V/c)2 qv=2. 5 Ge. V/c X=0. 5 2. 3 G e. V/c p
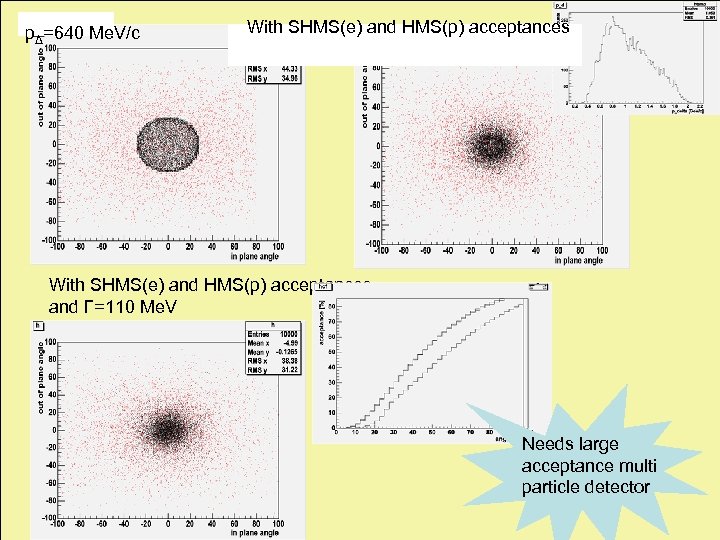
pΔ=640 Me. V/c With SHMS(e) and HMS(p) acceptances and Γ=110 Me. V Needs large acceptance multi particle detector
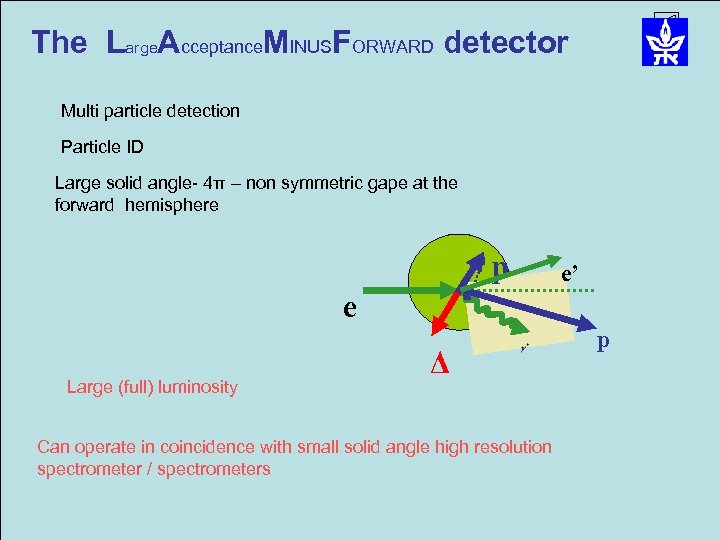
The Large. Acceptance. MINUSFORWARD detector Multi particle detection Particle ID Large solid angle- 4π – non symmetric gape at the forward hemisphere p e’ e Large (full) luminosity Δ Can operate in coincidence with small solid angle high resolution spectrometer / spectrometers p

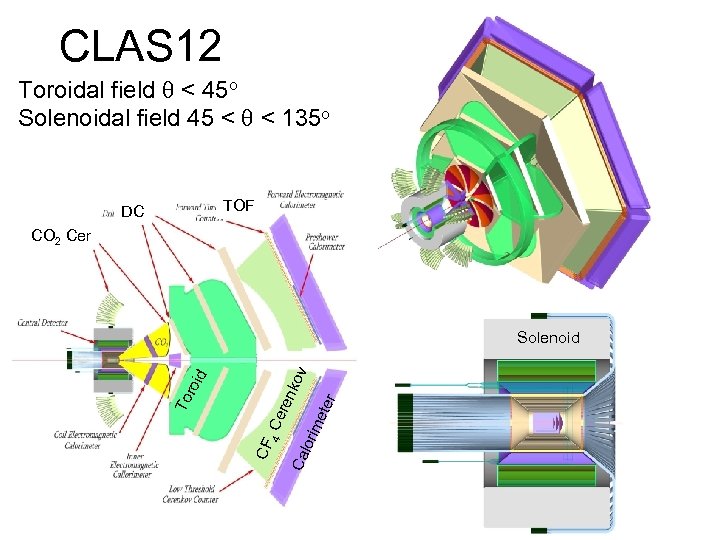
CLAS 12 Toroidal field < 45 o Solenoidal field 45 < < 135 o TOF DC CO 2 Cer ter me Ca lori ere 4 C CF To roi d nko v Solenoid
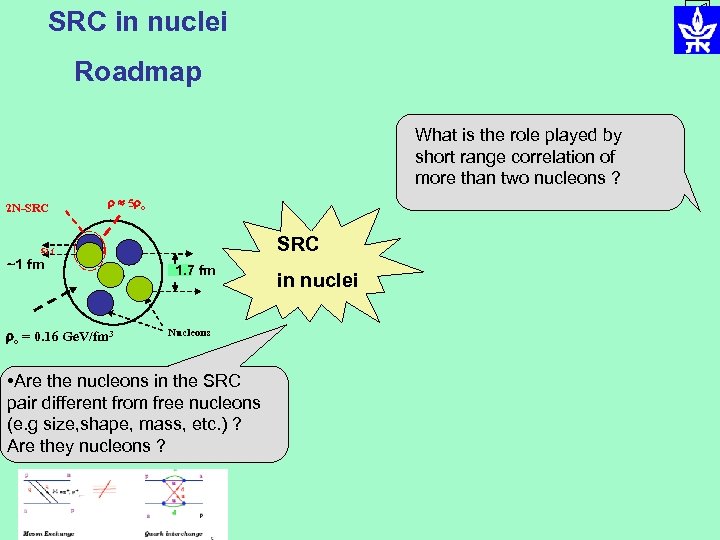
SRC in nuclei Roadmap What is the role played by short range correlation of more than two nucleons ? 2 N-SRC 5 o SRC 1. f ~1 fm o = 0. 16 Ge. V/fm 3 1. 7 fm 1. 7 f Nucleons • Are the nucleons in the SRC pair different from free nucleons (e. g size, shape, mass, etc. ) ? Are they nucleons ? in nuclei
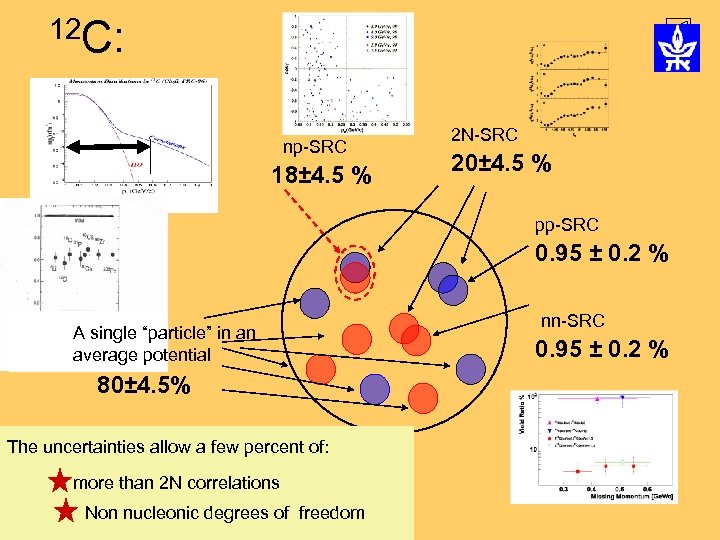
12 C: np-SRC 18± 4. 5 % 2 N-SRC 20± 4. 5 % pp-SRC 0. 95 ± 0. 2 % A single “particle” in an average potential 80± 4. 5% The uncertainties allow a few percent of: more than 2 N correlations Non nucleonic degrees of freedom nn-SRC 0. 95 ± 0. 2 %

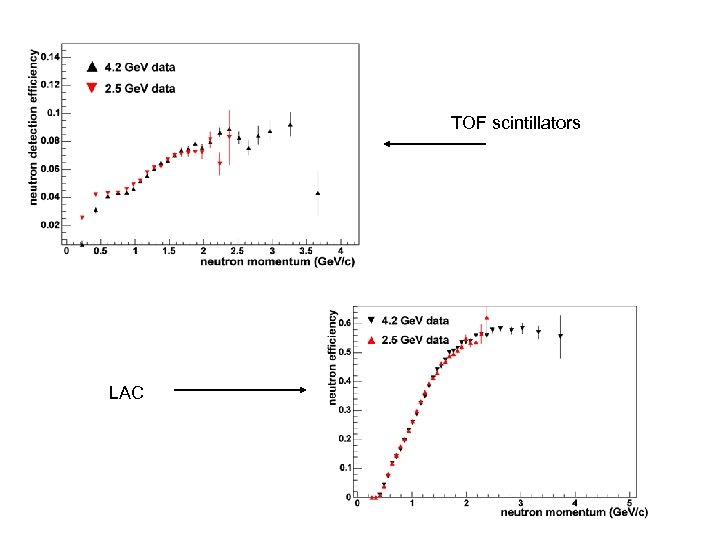
TOF scintillators LAC
bb1a63410c114df035deb2292dd1a05a.ppt