
B & A A→ Основы логики B Av. B Джордж Буль (1815 -1864) основоположник математической логики B ↔ A

Логика – это наука о формах и способах мышления.

1. Формы мышления Основные формы мышления: 1. Понятие 2. Высказывание 3. Умозаключение
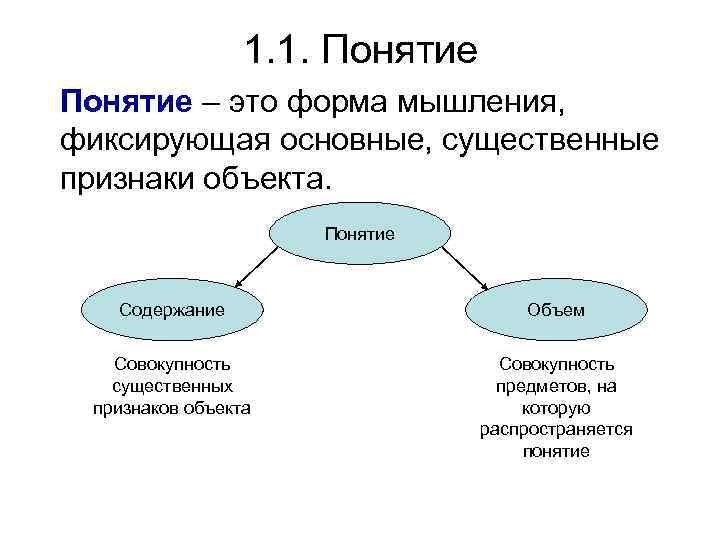
1. 1. Понятие – это форма мышления, фиксирующая основные, существенные признаки объекта. Понятие Содержание Объем Совокупность существенных признаков объекта Совокупность предметов, на которую распространяется понятие
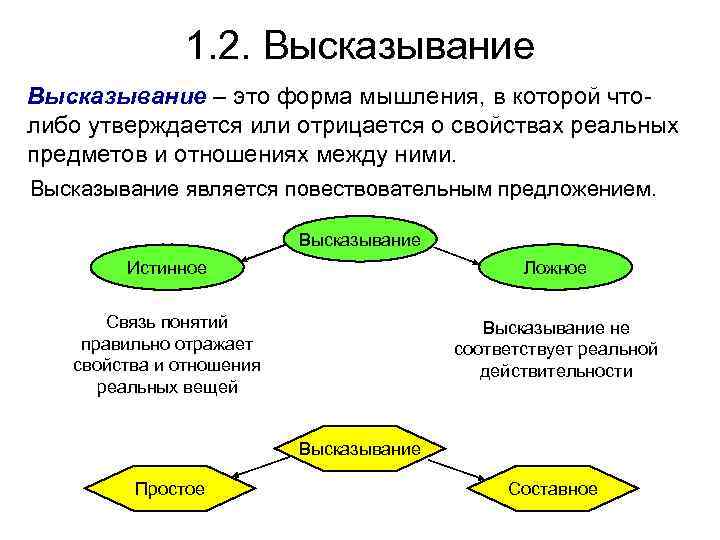
1. 2. Высказывание – это форма мышления, в которой чтолибо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание является повествовательным предложением. Высказывание Истинное Ложное Связь понятий правильно отражает свойства и отношения реальных вещей Высказывание не соответствует реальной действительности Высказывание Простое Составное

1. 3. Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение). Посылки – только истинные суждения.

2. Алгебра высказываний служит для определения истинности или ложности составных высказываний. Основные понятия: • логическая переменная • логическая функция • логическая операция

Логическая переменная Простое высказывание, содержащее только одну мысль. Ее символическое обозначение – латинская буква (А, Х, Y и т. д. ). Значением логической переменной могут быть только константы ИСТИНА и ЛОЖЬ (1 и 0).

Логическая функция Составное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций. Ее символическое обозначение – F(A, B, . . ).

Логические операции 2. 1. Логическое умножение (конъюнкция) 2. 2. Логическое сложение (дизъюнкция) 2. 3. Логическое отрицание (инверсия) 2. 4. Логическое следование (импликация) 2. 5. Логическое равенство (эквивалентность)

2. 1. Логическое умножение (конъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «и» . Составное высказывание истинно только тогда, когда истины оба простых высказывания. Соответствует союзу И Обозначение &, В языках программирования and; Таблица истинности A B A&B 0 0 1 1 1

2. 2. Логическое сложение (дизъюнкция) Объединение двух (или нескольких) высказываний в одно с помощью союза «или» . Составное высказывание истинно только тогда, когда истинно хотя бы одно из двух простых высказывания. Соответствует союзу ИЛИ Обозначение V В языках программирования or Таблица истинности A B Av. B 0 0 1 1 1

2. 3. Логическое отрицание (инверсия) Присоединение частицы «не» к высказыванию. Инверсия делает истинное высказывание ложным и, наоборот. Соответствует союзу НЕ Обозначение Ā, ¬А В языках программирования not Таблица истинности A Ā 0 1 1 0

2. 4. Логическое следование (импликация) Импликация образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…» . Импликация ложна только тогда, когда из истинного первого высказывания(предпосылки) следует ложный вывод (второе высказывание). Соответствует обороту Если…, то… Обозначение А→В В языках программирования if … then … Таблица истинности A B A→B 0 0 1 0 1 1 1

2. 5. Логическое равенство (эквивалентность) Эквивалентность образуется соединением двух высказываний в одно с помощью оборота речи «… тогда и только тогда, когда …» . Составное высказывание, образованное с помощью логической операции эквивалентности истинно тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны. Соответствует обороту тогда и только тогда, когда … Обозначение А≡В, А~B Таблица истинности A B А~B 0 0 1 0 1 0 0 1 1 1

3. Логические выражения и таблицы истинности Логическое выражение – формула, в которую входят логические переменные и знаки логических операций. Пример: Порядок выполнения логических операций: 1. Действия в скобках. 2. Инверсия, конъюнкция, дизъюнкция, импликация, эквивалентность. Для логического выражения можно построить таблицу истинности, которая определяет его истинность или ложность при всех возможных комбинациях исходных значений простых высказываний.

4. Построение таблицы истинности 1. Определить количество строк в таблице по формуле 2 n, где n – количество логических переменных. 2. Определить количество столбцов таблицы: количество логических переменных + количество логических операций. 3. Построить таблицу истинности, обозначить столбцы, внести всевозможные наборы исходных данных логических переменных. 4. Заполнить таблицу истинности, выполняя базовые логические операции в необходимой последовательности.
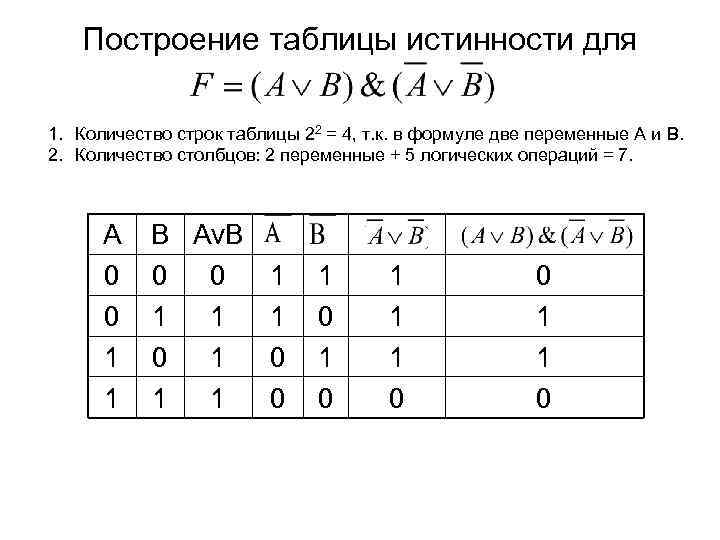
Построение таблицы истинности для 1. Количество строк таблицы 22 = 4, т. к. в формуле две переменные A и B. 2. Количество столбцов: 2 переменные + 5 логических операций = 7. A 0 0 1 1 B Av. B 0 0 1 1 0 1 0 1 1 1 0 0 1 1 0

Равносильные логические выражения - это выражения, у которых последние столбцы таблиц истинности совпадают, обозначают “=“. Докажите равносильность выражений: Таблица истинности для A 0 0 1 1 B 0 1 Av. B 0 1 1 1 Таблица истинности для 1 0 0 0 A 0 0 1 1 B 0 1 1 1 0 0 1 0 1 0 0 0

Законы логики и правила преобразования логических выражений Если логическое выражение содержит большое число операций, то составлять для него таблицу истинности достаточно сложно, т. к. приходится перебирать большое количество вариантов. В таких случаях формулы удобно привести к нормальной форме. Нормальная форма – форма, в которой отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при логических переменных.

Законы коммутативности х у=у х

Законы ассоциативности (x у) z=x (у z) (х у) z=х (у z)

Законы поглощения (нуля и единицы) х 0=х х 1=1 х 0=0 х 1=х

Законы дистрибутивности х (у z)=(х у) (х z)
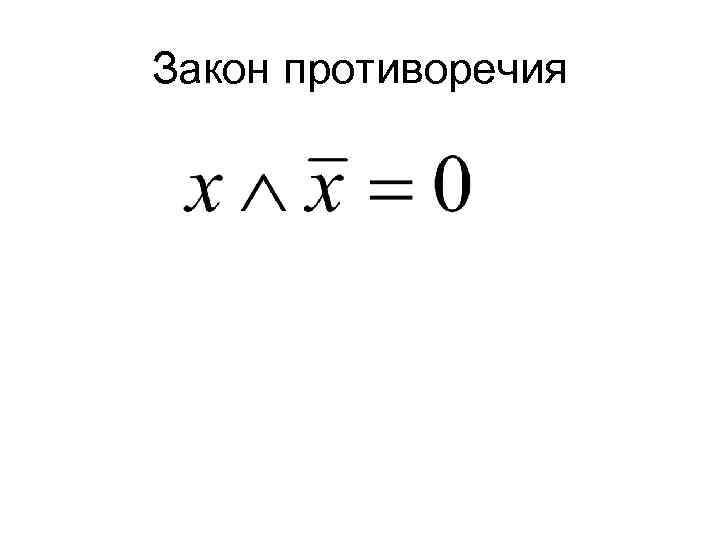
Закон противоречия
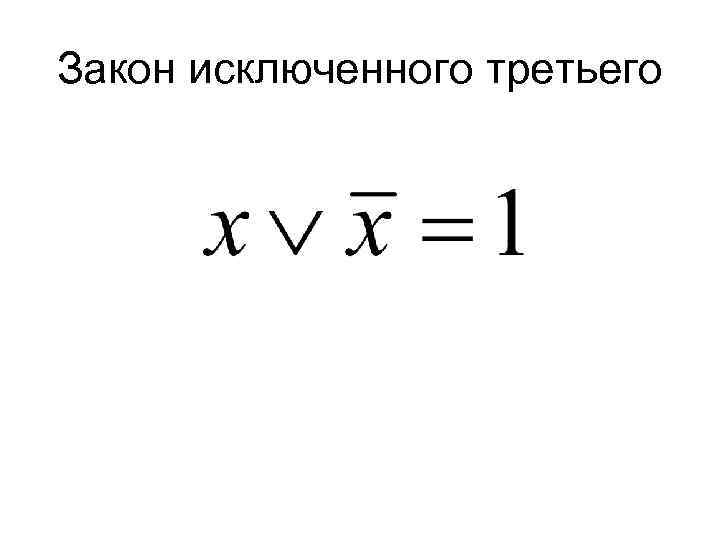
Закон исключенного третьего

Законы идемпотентности х х=х
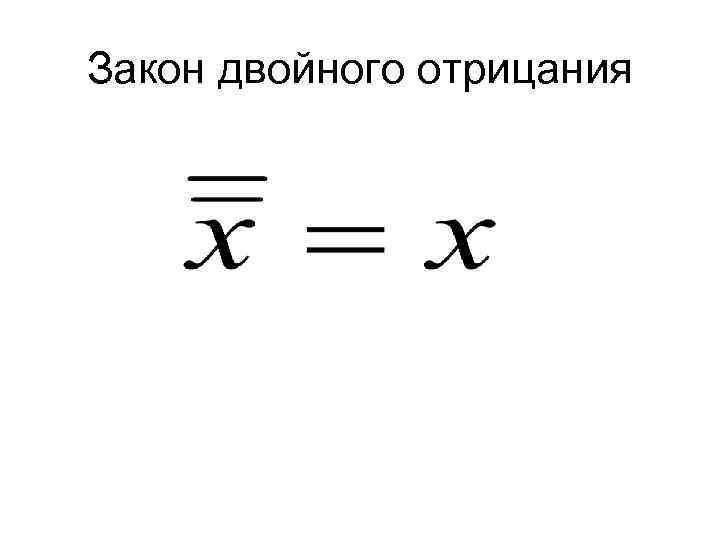
Закон двойного отрицания

Законы де Моргана
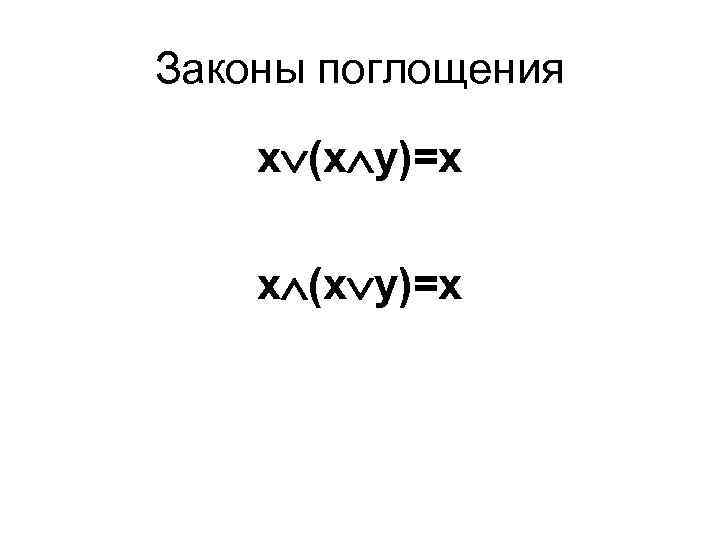
Законы поглощения x (x у)=х х (х у)=х
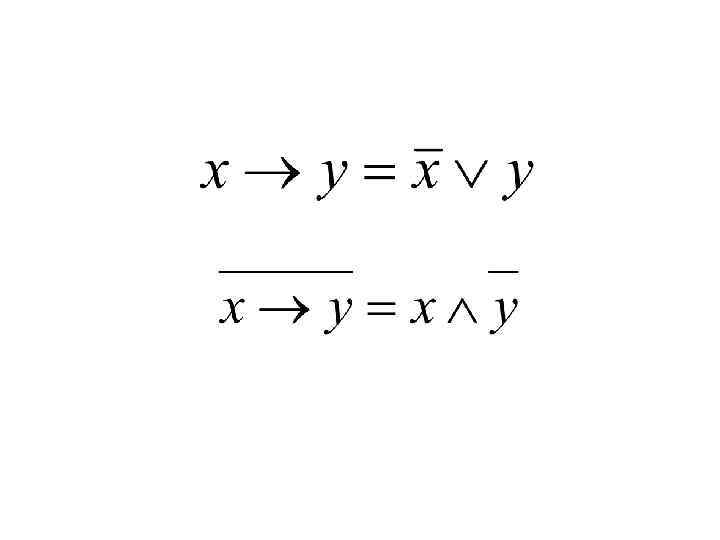

Методы решения логических задач

Формальный способ решения логических задач 1. 2. 3. 4. 5. 6. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами. Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций. Составить единое логическое выражение для всех требований задачи. Используя законы алгебры логики, попытаться упростить полученное выражение и вычислить все его значения либо построить таблицу истинности для рассматриваемого выражения. Выбрать решение — набор значений простых высказываний, при котором построенное логическое выражение является истинным. Проверить, удовлетворяет ли полученное решение условию задачи.
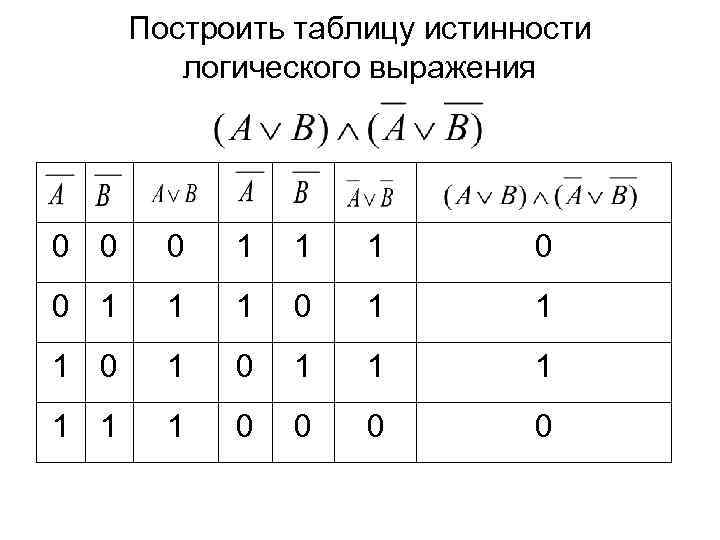
Построить таблицу истинности логического выражения 0 0 0 1 1 1 0 1 1 1 0 0

1. На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй» . Кто из учащихся изучал логику? P 1 – первый изучал логику P 1 – второй изучал логику P 1 – третий изучал логику

Упростите логическую формулу

Задача «Кто виноват? » По обвинению в ограблении перед судом предстали Иванов, Петров, Сидоров. Следствием установлено: если Иванов не виновен или Петров виновен, то Сидоров виновен; если Иванов не виновен, то Сидоров не виновен. Виновен ли Иванов? В С F 0 0 0 1 1 0 0 1 1 Решить данную задачу — значит указать, при каких значениях А полученное сложное высказывание F истинно. Для этого необходимо проанализировать все строки таблицы истинности, где F=1. И если хотя бы в одном из таких случаев А=0 (Иванов не виновен), то у следствия недостаточно фактов для того, чтобы обвинить Иванова в преступлении. Анализ таблицы показывает, что высказывание F истинно только в тех случаях, когда А истинно, т. е. Иванов в ограблении виновен. А 0 А = {Иванов виновен}, В = {Петров виновен}, С = {Сидоров виновен}. 0 1 1 0 0 1 1