b a α a b α где 0

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕГИСТРАЦИЯ

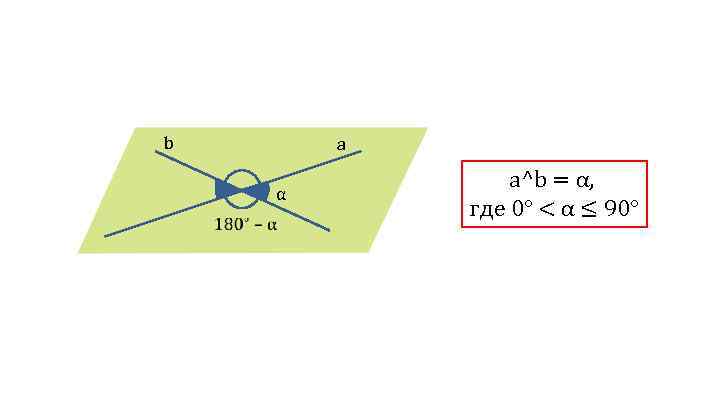
b a α a^b = α, где 0° < α ≤ 90°

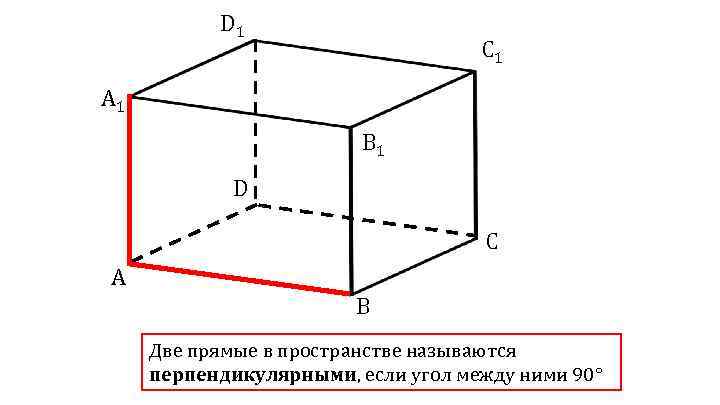
D 1 C 1 A 1 B 1 D C A B Две прямые в пространстве называются перпендикулярными, если угол между ними 90°

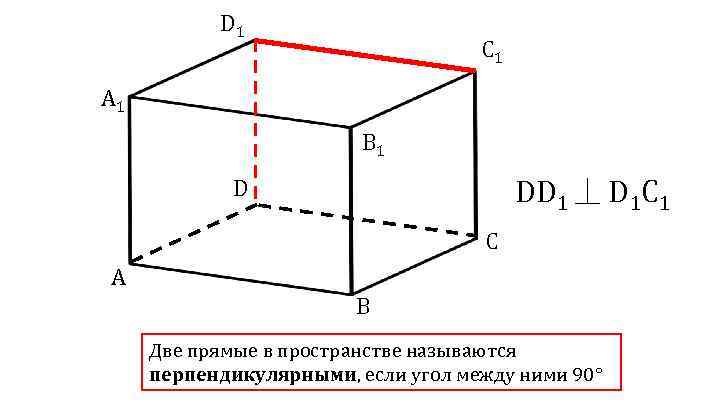
D 1 C 1 A 1 B 1 DD 1 ⏊ D 1 C 1 D C A B Две прямые в пространстве называются перпендикулярными, если угол между ними 90°

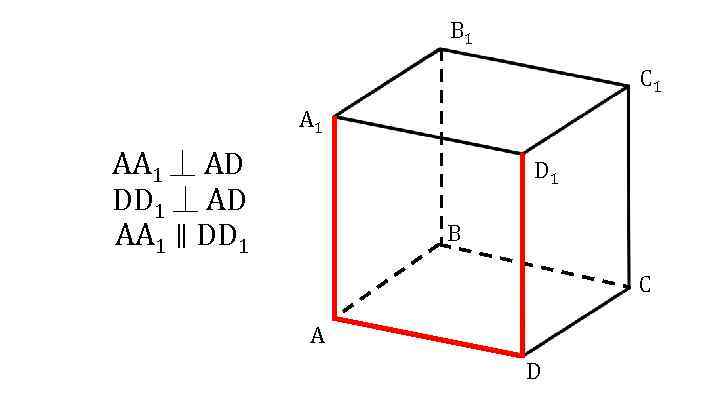
B 1 C 1 AA 1 ⏊ АD DD 1 ⏊ АD AA 1 ∥ DD 1 B C A D

Лемма (о перпендикулярности двух параллельных прямых третьей прямой) Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой

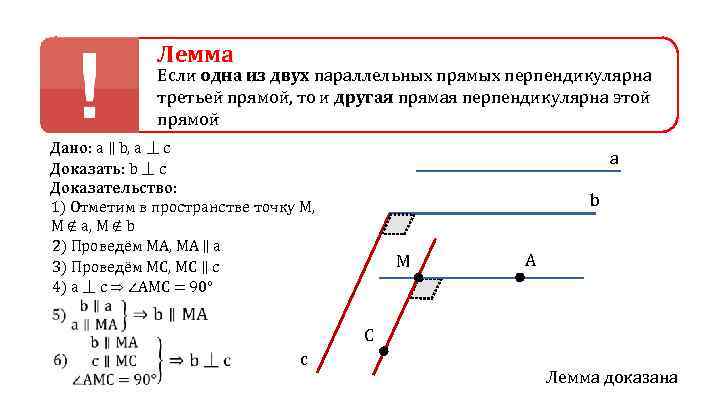
Лемма Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая прямая перпендикулярна этой прямой Дано: а ∥ b, a ⏊ c Доказать: b ⏊ c Доказательство: 1) Отметим в пространстве точку М, М ∉ a, М ∉ b 2) Проведём МА, МА ∥ a 3) Проведём МС, МС ∥ с 4) a ⏊ c ⇒ ∠АМС = 90° a b M A C c Лемма доказана

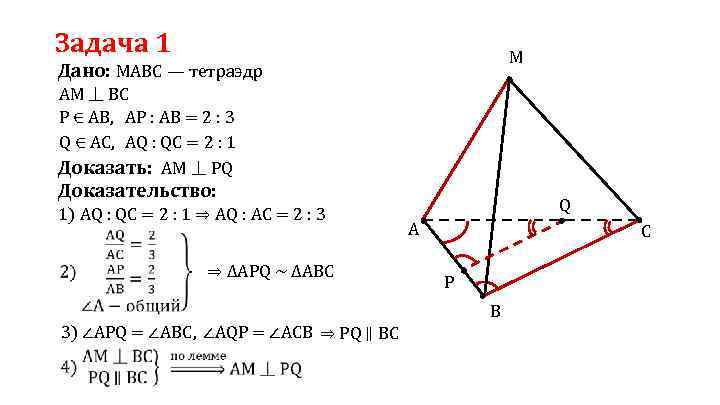
Задача 1 M Дано: МАВС — тетраэдр АМ ⏊ BC Р ∈ АВ, АР : АВ = 2 : 3 Q ∈ АС, АQ : QC = 2 : 1 Доказать: АМ ⏊ PQ Доказательство: 1) АQ : QС = 2 : 1 ⇒ АQ : АС = 2 : 3 ⇒ ∆АPQ ∼ ∆АBС Q C A P B 3) ∠АРQ = ∠АВС, ∠АQР = ∠АСВ ⇒ РQ ∥ ВС

Скачать презентацию b a α a b α где 0

15. Перпендикулярные прямые в пространстве.ppt

Количество слайдов: 8