8b0d1f2a6a70d51d965f15a25edd119f.ppt
- Количество слайдов: 82

B 3 LYP augmented with an empirical dispersion term (B 3 LYP-D*) as applied to solids Bartolomeo Civalleri Theoretical Chemistry Group Department of Chemistry IFM & NIS Centre of Excellence University of Torino bartolomeo. civalleri@unito. it Vallico Sotto July 2009

Weak interactions in crystalline solids • Cohesive forces • long-range: electrostatic, induction, dispersion • short-range: exchange repulsion, charge transfer • Weak interactions play an important role in the solid state (see T. Steiner, Angew. Chem. Int. Ed. 41 (2002) 48) • Molecular recognition crystal packing • Supramolecular chemistry and crystalline engineering • • • Molecular crystals (polymorphism) Layered and composite/intercalated materials Adsorption and reactivity on surfaces • Very important for many properties of interest: structure, interaction energies, vibrational frequencies and thermodynamics, elastic frequencies constants, relative stability, … Vallico Sotto July 2009
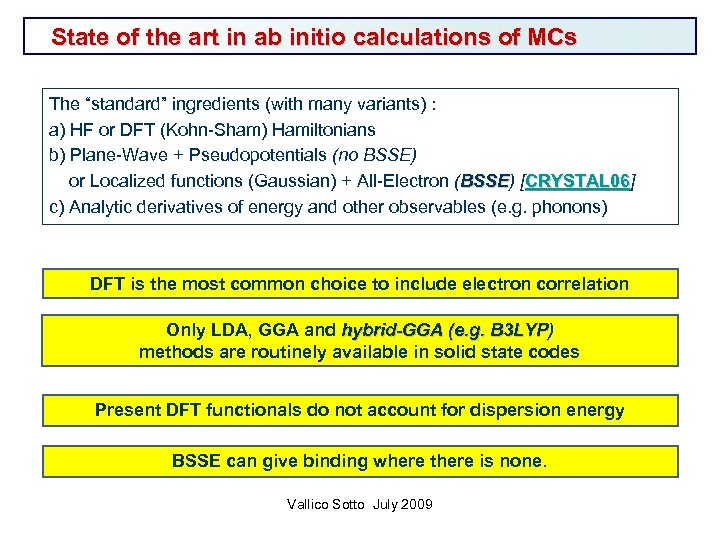
State of the art in ab initio calculations of MCs The “standard” ingredients (with many variants) : a) HF or DFT (Kohn-Sham) Hamiltonians b) Plane-Wave + Pseudopotentials (no BSSE) or Localized functions (Gaussian) + All-Electron (BSSE) [CRYSTAL 06] BSSE CRYSTAL 06 c) Analytic derivatives of energy and other observables (e. g. phonons) DFT is the most common choice to include electron correlation Only LDA, GGA and hybrid-GGA (e. g. B 3 LYP) methods are routinely available in solid state codes Present DFT functionals do not account for dispersion energy BSSE can give binding where there is none. Vallico Sotto July 2009
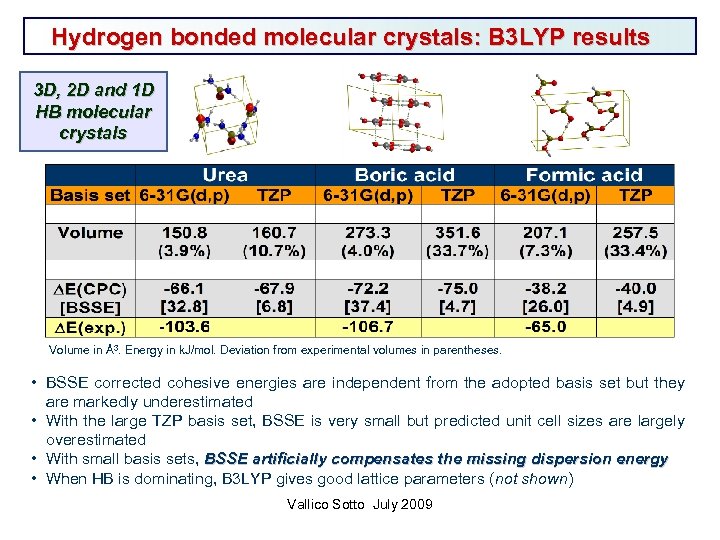
Hydrogen bonded molecular crystals: B 3 LYP results 3 D, 2 D and 1 D HB molecular crystals Volume in Å3. Energy in k. J/mol. Deviation from experimental volumes in parentheses. • BSSE corrected cohesive energies are independent from the adopted basis set but they are markedly underestimated • With the large TZP basis set, BSSE is very small but predicted unit cell sizes are largely overestimated • With small basis sets, BSSE artificially compensates the missing dispersion energy • When HB is dominating, B 3 LYP gives good lattice parameters (not shown) Vallico Sotto July 2009

DFT vs vd. W forces: new hopes… How to deal with dispersion interactions in DFT? • New functionals: - vd. W-DFT (Langreth, Lundqvist and co-workers) - beyond m-GGA (Perdew’s “Jacob’s Ladder” – fifth rung) - screened Coulomb (or CAM) functionals (Scuseria, Handy, Savin, Hirao, …) - Truhlar’s family (M 05, M 05 -X, M 06, …) • Perturbational electron-interaction corrections - on top of range-separated hybrids (Savin and coworkers: e. g. Goll et al. PCCP (2005)) - double-hybrids (Grimme JCP 124 (2006) 034108, Head-Gordon JPC-A (2008) ) • A pragmatic approach: Wilson-Levy (WL) correlation functional (a-posteriori HF) (T. A. Walsh, PCCP 7 (2005) 403; B. Civalleri et al. CPL 451 (2008) 287) • Empirical corrections by adding a -C 6/R 6 term (Grimme, Neumann, Yang, Zimmerli, Scoles, …) • A DF model of the dispersion interaction: C 6 in terms of exchange-hole dipole moment (Becke-Johnson, JCP 123 (2005) 024101, JCP 124 (2006) 014104, JCP 127 (2007) 154108) or C 6 from MLWFs (Silvestrelli, PRL 100 (2008) 053002) • Dispersion-corrected atom centered pseudo-potentials (U. Rothlisberger and co-workers: e. g. Tapavicza et al. JCTC (2007), G. Di. Labio CPL (2008)) Vallico Sotto July 2009

Empirical –C 6/R 6 correction: Grimme’s model S. Grimme, J. Comput. Chem. , 2004, 25, 1463 and J. Comput. Chem. , 2006, 27, 1787 Atom-atom additive damped empirical potential of the form -f(R)C 6/R 6 where • s 6: scaling factor for each DFT method (s 6=1. 05 for B 3 LYP) • C 6 ij are computed from atomic dispersion coefficients: C 6 ij = C 6 i·C 6 j • Rvdw is the sum of atomic van der Waals radii: Rvdw=Rivdw+Rjvdw • d determines the steepness of the damping function (d=20) • summation over g truncated at 25 Å (estimated error < 0. 02 k. J/mol on DE) • Grimme proposed a set of parameters (i. e. C 6 i and Rivdw) from H to Xe Total energy is then computed as: Implemented in CRYSTAL 06 for energy and gradients (atoms and cell): CRYSTAL 06 B. Civalleri, C. M. Zicovich-Wilson, et al. , Cryst. Eng. Comm, 2008, DOI: 10. 1039/b 715018 k (see supplementary material for erratum) Vallico Sotto July 2009

GRIMME input block E. g. : Urea – B 3 LYP-D Urea CRYSTAL 0 0 0 113 5. 565 4. 684 5 6 0. 0000 0. 5000 0. 3260 8 0. 0000 0. 5953 7 0. 1459 0. 6459 0. 1766 1 0. 2575 0. 7575 0. 2827 1 0. 1441 0. 6441 -0. 0380 Optional keywords END (ENDG) Basis set END … GRIMME 1. 05 20. 4 1 0. 14 6 1. 75 7 1. 23 8 0. 70 … END 25. 1. 001 1. 452 1. 397 1. 342 Grimme empirical dispersion keyword s 6 (scaling factor) d (steepness) Rcut (cut-off radius, Å) Nr. of atomic species Atomic number C 6 (Jnm 6 mol− 1) Rvdw (Å) Atomic number C 6 Rvdw End of SCF&method input section Vallico Sotto July 2009 8
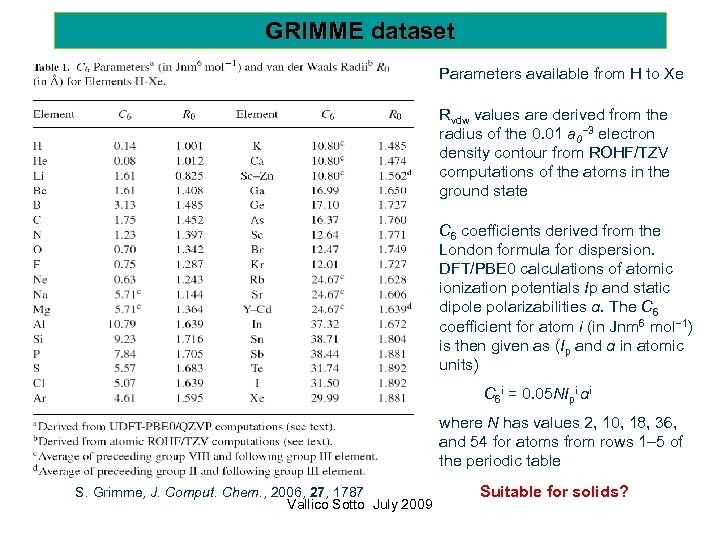
GRIMME dataset Parameters available from H to Xe Rvdw values are derived from the radius of the 0. 01 a 0− 3 electron density contour from ROHF/TZV computations of the atoms in the ground state C 6 coefficients derived from the London formula for dispersion. DFT/PBE 0 calculations of atomic ionization potentials Ip and static dipole polarizabilities α. The C 6 coefficient for atom i (in Jnm 6 mol− 1) is then given as (Ip and α in atomic units) C 6 i = 0. 05 NIpi αi where N has values 2, 10, 18, 36, and 54 for atoms from rows 1– 5 of the periodic table S. Grimme, J. Comput. Chem. , 2006, 27, 1787 Vallico Sotto July 2009 Suitable for solids?
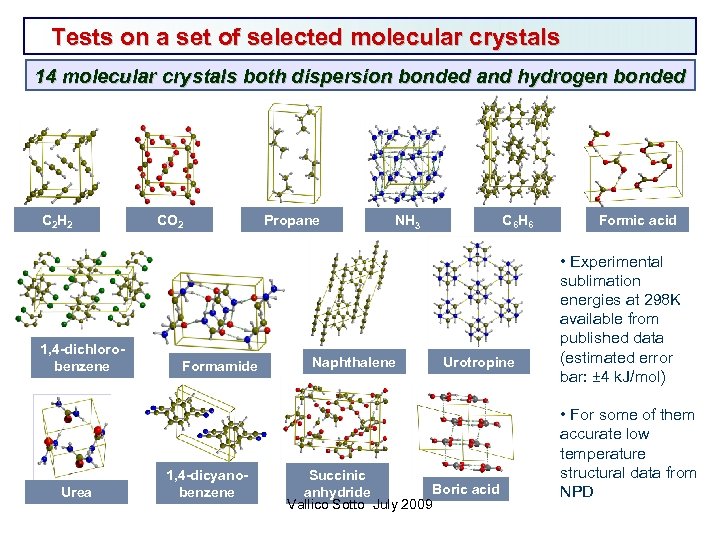
Tests on a set of selected molecular crystals 14 molecular crystals both dispersion bonded and hydrogen bonded C 2 H 2 1, 4 -dichlorobenzene Urea CO 2 Formamide 1, 4 -dicyanobenzene Propane C 6 H 6 NH 3 Naphthalene Urotropine Succinic Boric acid anhydride Vallico Sotto July 2009 Formic acid • Experimental sublimation energies at 298 K available from published data (estimated error bar: ± 4 k. J/mol) • For some of them accurate low temperature structural data from NPD
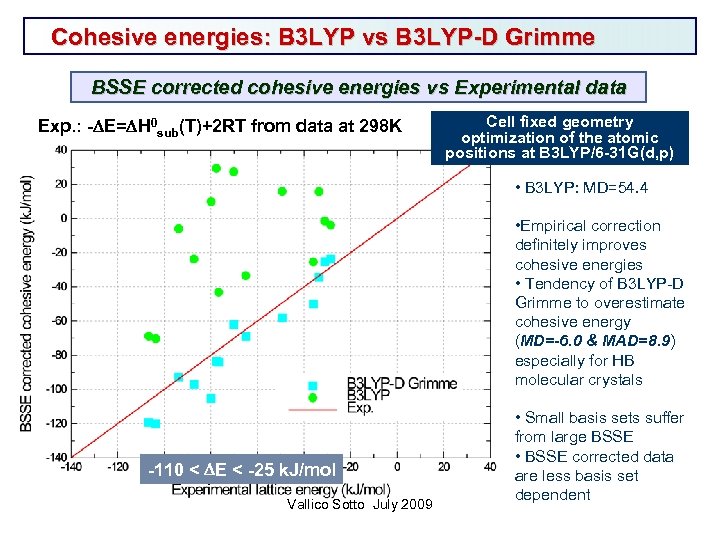
Cohesive energies: B 3 LYP vs B 3 LYP-D Grimme BSSE corrected cohesive energies vs Experimental data Exp. : -DE=DH 0 sub(T)+2 RT from data at 298 K Cell fixed geometry optimization of the atomic positions at B 3 LYP/6 -31 G(d, p) • B 3 LYP: MD=54. 4 • Empirical correction definitely improves cohesive energies • Tendency of B 3 LYP-D Grimme to overestimate cohesive energy (MD=-6. 0 & MAD=8. 9) especially for HB molecular crystals -110 < DE < -25 k. J/mol Vallico Sotto July 2009 • Small basis sets suffer from large BSSE • BSSE corrected data are less basis set dependent
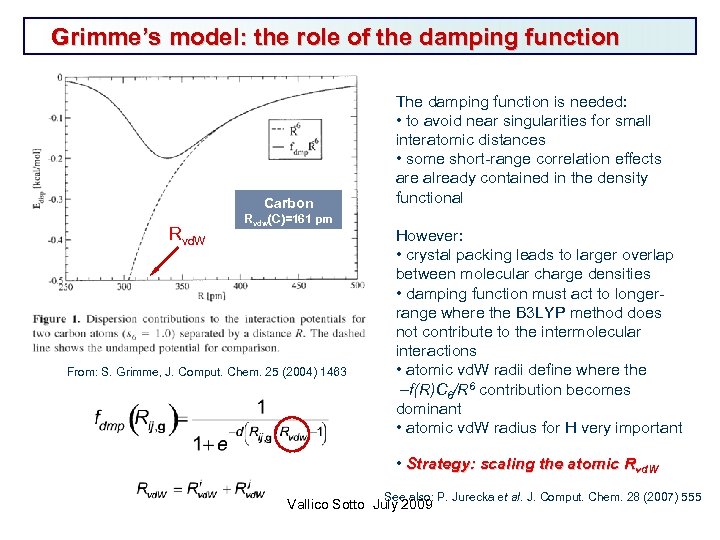
Grimme’s model: the role of the damping function Carbon Rvd. W Rvdw(C)=161 pm From: S. Grimme, J. Comput. Chem. 25 (2004) 1463 The damping function is needed: • to avoid near singularities for small interatomic distances • some short-range correlation effects are already contained in the density functional However: • crystal packing leads to larger overlap between molecular charge densities • damping function must act to longerrange where the B 3 LYP method does not contribute to the intermolecular interactions • atomic vd. W radii define where the –f(R)C 6/R 6 contribution becomes dominant • atomic vd. W radius for H very important • Strategy: scaling the atomic Rvd. W See also: P. Jurecka et al. J. Comput. Chem. 28 (2007) 555 Vallico Sotto July 2009
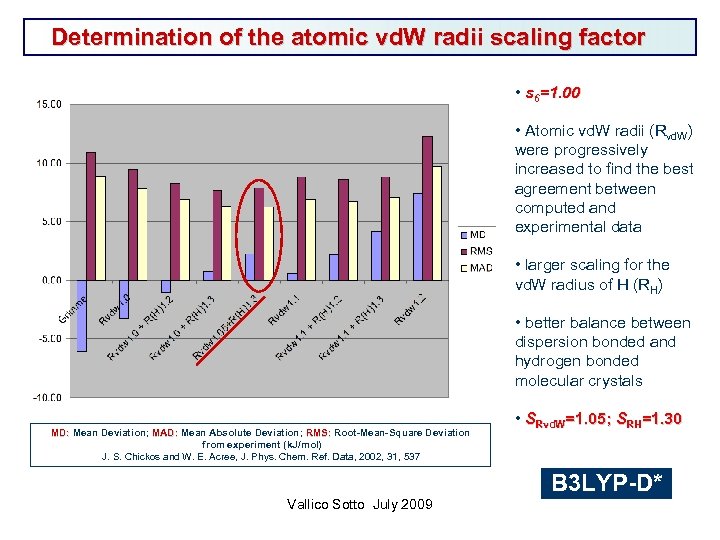
Determination of the atomic vd. W radii scaling factor • s 6=1. 00 • Atomic vd. W radii (Rvd. W) were progressively increased to find the best agreement between computed and experimental data • larger scaling for the vd. W radius of H (RH) • better balance between dispersion bonded and hydrogen bonded molecular crystals MD: Mean Deviation; MAD: Mean Absolute Deviation; RMS: Root-Mean-Square Deviation MD: MAD: RMS: from experiment (k. J/mol) J. S. Chickos and W. E. Acree, J. Phys. Chem. Ref. Data, 2002, 31, 537 • SRvd. W=1. 05; SRH=1. 30 B 3 LYP-D* Vallico Sotto July 2009

Cohesive energies with B 3 LYP-D* BSSE corrected cohesive energies vs Experimental data Exp. : -DE=DH 0 sub(T)+2 RT from data at 298 K Cell fixed geometry optimization of the atomic positions at B 3 LYP/6 -31 G(d, p) • B 3 LYP-D* gives cohesive energies in excellent agreement with experimental data • MD=2. 2 & MAD=6. 3 • Better balance between hydrogen bonded and dispersion bonded molecular crystals Vallico Sotto July 2009

Geometry optimization: B 3 LYP-D Grimme vs B 3 LYP-D* Lattice parameters • TZP basis set suffers from a remarkably small BSSE TZP ______ • B 3 LYP/TZP largely overestimates lattice parameters 6 -31 G(d, p) - - • B 3 LYP-D* lattice parameters are in excellent agreement with experimental data NH 3 C 2 H 2 CO 2 Urotropine Urea Vallico Sotto July 2009 C 6 H 6 • B 3 LYP-D (Grimme) gives too short lattice constants
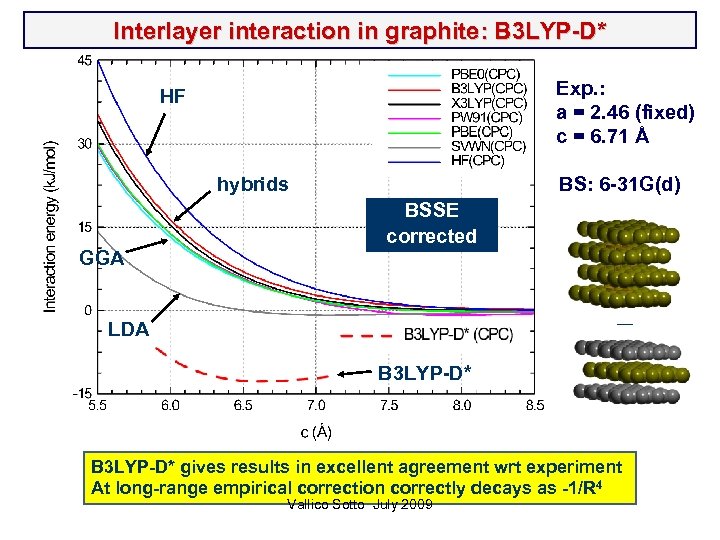
Interlayer interaction in graphite: B 3 LYP-D* Exp. : a = 2. 46 (fixed) c = 6. 71 Å HF hybrids GGA BS: 6 -31 G(d) BSSE corrected __ LDA B 3 LYP-D* gives results in excellent agreement wrt experiment At long-range empirical correction correctly decays as -1/R 4 Vallico Sotto July 2009
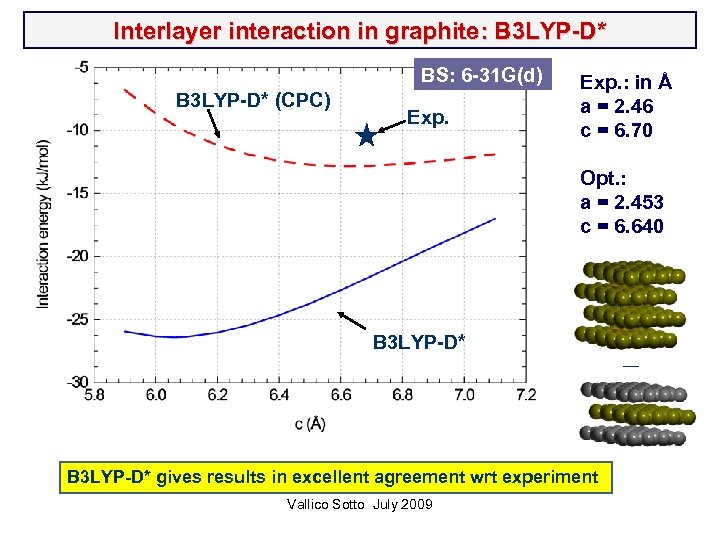
Interlayer interaction in graphite: B 3 LYP-D* (CPC) BS: 6 -31 G(d) Exp. : in Å a = 2. 46 c = 6. 70 Opt. : a = 2. 453 c = 6. 640 B 3 LYP-D* gives results in excellent agreement wrt experiment Vallico Sotto July 2009 __

Interlayer interaction in graphite: B 3 LYP-D* long-range 1/R 4 At long-range empirical London-type formula correctly decays as -1/R 4 Vallico Sotto July 2009
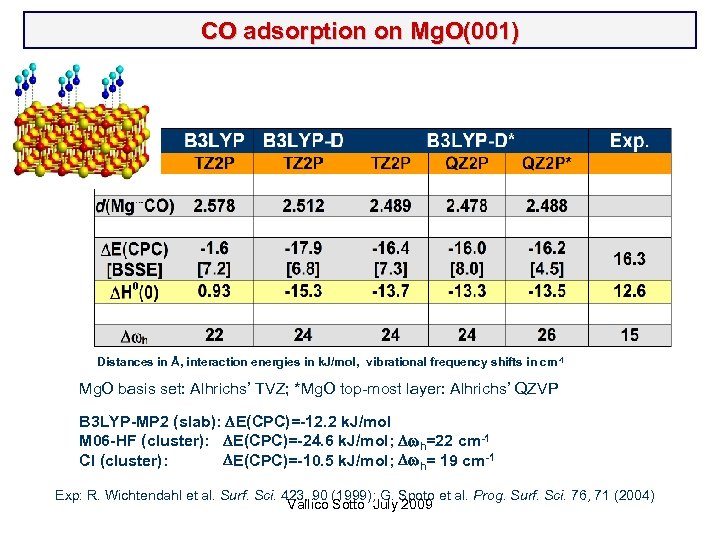
CO adsorption on Mg. O(001) Distances in Å, interaction energies in k. J/mol, vibrational frequency shifts in cm-1 Mg. O basis set: Alhrichs’ TVZ; *Mg. O top-most layer: Alhrichs’ QZVP B 3 LYP-MP 2 (slab): DE(CPC)=-12. 2 k. J/mol M 06 -HF (cluster): DE(CPC)=-24. 6 k. J/mol; Dwh=22 cm-1 CI (cluster): DE(CPC)=-10. 5 k. J/mol; Dwh= 19 cm-1 Exp: R. Wichtendahl et al. Surf. Sci. 423, 90 (1999); G. Spoto et al. Prog. Surf. Sci. 76, 71 (2004) Vallico Sotto July 2009

Conclusions Dispersion interactions are crucial and must be taken into account For molecular crystals: • Grimme’s scheme Recalibration needed • Useful tool to correct the PES. Electron density is indirectly influenced • It gives results in excellent agreement wrt experiment for cohesive energies and structures. • Lattice modes also well reproduced • A large basis set should be adopted (e. g. TZP) to reduce the BSSE In perspective: • Work is in progress to test the transferability of B 3 LYP-D* to alkali halides (e. g. which C 6 for Li+, Na+, …? ) • C 6 from non-empirical models (e. g. Becke-Johnson, Silvestrelli, …) Vallico Sotto July 2009

Calculation of vibrational frequencies and tools for their analysis with CRYSTAL 06 R. Dovesi (Torino ) L. Valenzano (Torino) C. Zicovich (Cuernavaca) Y. Noël (Paris) F. Pascale (Nancy) Vallico Sotto July 2009 21

The CRYSTAL code: Quantum-Mechanical, ab-initio, periodic, using a local basis set (“Atomic Orbitals”) Vallico Sotto July 2009 22

CRYSTA 06 web site www. crystal. unito. it Vallico Sotto July 2009

A few historical references Formulation and implementation (graphite) • • C. Pisani and R. Dovesi Exact exchange Hartree-Fock calculations for periodic systems. I. Illustration of the method. Int. J. Quantum Chem. 17, 501 -516 (1980). R. Dovesi, C. Pisani and C. Roetti Exact exchange Hartree-Fock calculations for periodic systems. II. Results for graphite and hexagonal boron nitride Int. J. Quantum Chem 17, 517 -529 (1980). The Coulomb problem: multipolar expansion+Ewald • R. Dovesi, C. Pisani, C. Roetti and V. R. Saunders Treatment of Coulomb interactions in Hartree-Fock calculations of periodic systems. Phys. Rev. B 28, 5781 -5792 (1983). • V. R. Saunders, C. Freyria-Fava, R. Dovesi, L. Salasco and C. Roetti On the electrostatic potential in crystalline systems where the charge density is expanded in Gaussian functions. Mol. Phys. 77, 629 -665 (1992) • V. R. Saunders, C. Freyria-Fava, R. Dovesi and C. Roetti On the electrostatic potential in linear periodic polymers. Comp. Phys. Comm. 84, 156 -172 (1994) Towards the hybrids. . . . M. Causà, R. Dovesi, C. Pisani, R. Colle and A. Fortunelli Correlation correction to the Hartree-Fock total energy of solids. Phys. Rev. B 36, 891 -897 (1987). Vallico Sotto July 2009 24

The periodic model • Consistent treatment of Periodicity – 3 D - Crystalline solids (230 space groups) – 2 D - Films and surfaces (80 layer groups) – 1 D – Polymers (75 rod groups) – 0 D – Molecules (32 point groups) • Infinite sums of particle interactions – Ewald's method – Specific formulæ for 1 D, 2 D, 3 D • Full exploitation of symmetry – in direct space – in reciprocal space Vallico Sotto July 2009 25

Hamiltonians • Restricted and Unrestricted Hartree-Fock Theory • Total and Spin Density Functional Theory Local functionals [L] and gradient-corrected [G] exchange-correlation functionals Correlation functionals Ø Vosko-Willk-Nusair (VWN 5 parameterization) [L] Ø Perdew-Wang [L] Ø Perdew-Zunger '81 [L] Ø von Barth-Hedin [L] Ø Lee-Yang-Parr [G] Hybrid DFT-HF exchange functionals Ø Perdew '86 [G] ØB 3 PW, B 3 LYP (using the VWN 5 Ø Perdew-Wang '91 [G] functional) Ø Perdew-Burke-Ernzerhof ØUser-definable hybrid functionals [G] Exchange functionals Ø Slater [L] Ø von Barth-Hedin [L] Ø Becke '88 [G] Ø Perdew-Wang '91 [G] Ø Perdew-Burke-Ernzerhof [G] Vallico Sotto July 2009 26

The basis set Crystalline orbitals as linear combinations of Bloch Functions as linear combinations of Atomic Orbitals as contractions of Hermite Gaussian functions Vallico Sotto July 2009

Running CRYSTAL 2006 Software performance Supported platforms • Memory management: • Pentium and Athlon based dynamic allocation systems with Linux • Efficient storage of integrals or • IBM workstations and clusters Direct SCF with AIX 4. 2 or 4. 3 • SGI workstations and servers • Full parallelization (MPI) – Replicated data version – Massive parallel version up 2048 processors (soon available) • • DEC Alpha workstations HP-UX systems Sun Solaris Linux Alpha Vallico Sotto July 2009 28

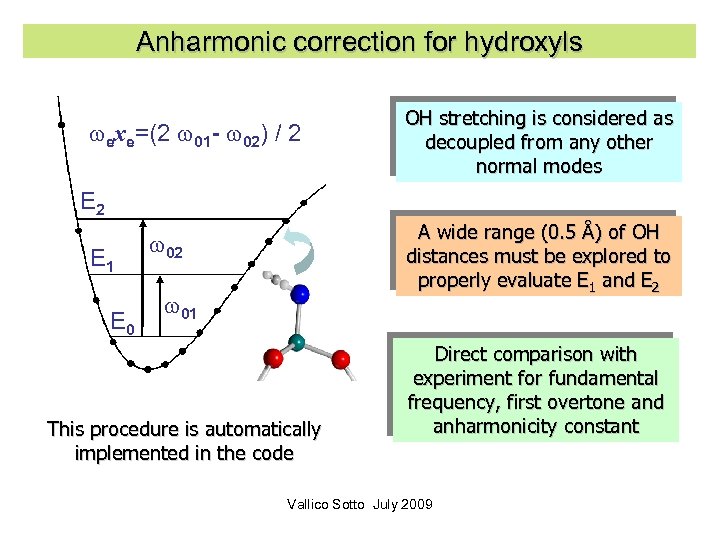
The problem of H It is well known that the stretching modes involving hydrogen atoms are strongly anharmonic: typically for the O-H stretching anharmonicity can be as large as 180 cm-1. However this difficulty is compensated by the full separability of this mode. Vallico Sotto July 2009 29
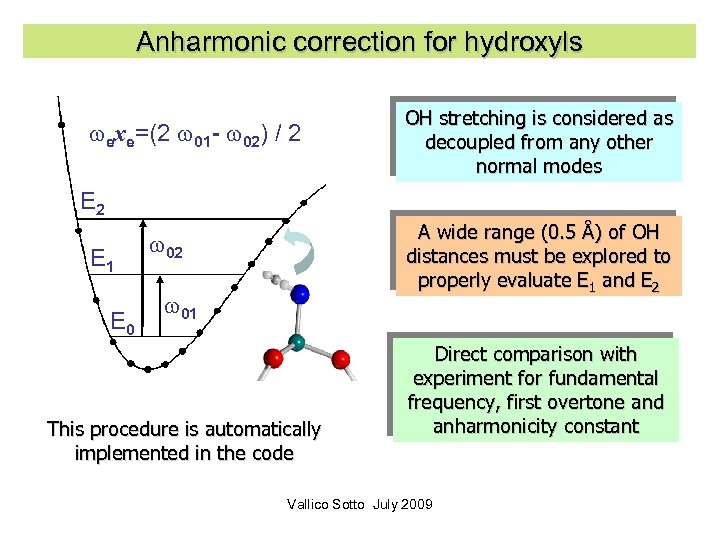
Anharmonic correction for hydroxyls exe=(2 01 - 02) / 2 OH stretching is considered as decoupled from any other normal modes E 2 E 1 E 0 A wide range (0. 5 Å) of OH distances must be explored to properly evaluate E 1 and E 2 02 01 This procedure is automatically implemented in the code Direct comparison with experiment for fundamental frequency, first overtone and anharmonicity constant Vallico Sotto July 2009
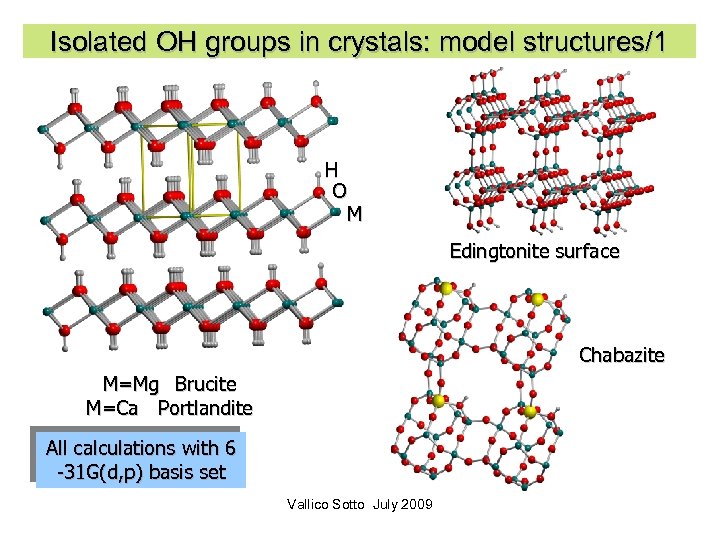
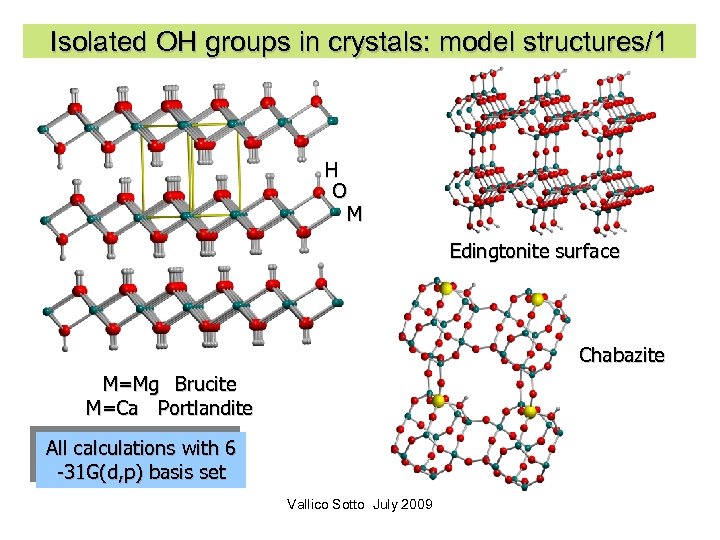
Isolated OH groups in crystals: model structures/1 H O M Edingtonite surface Chabazite M=Mg Brucite M=Ca Portlandite All calculations with 6 -31 G(d, p) basis set Vallico Sotto July 2009

B 3 LYP vs experimental OH frequencies Vallico Sotto July 2009
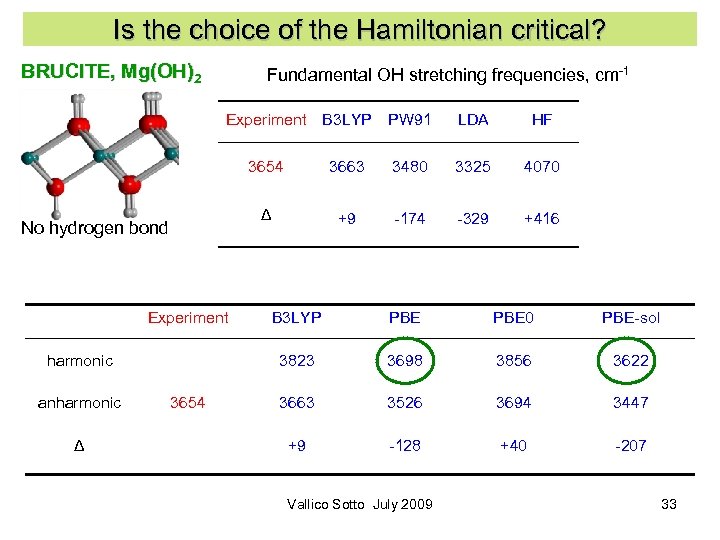
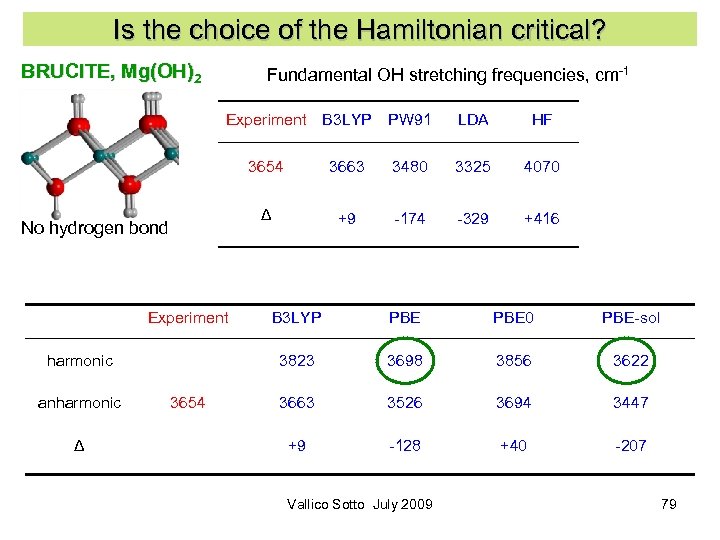
Is the choice of the Hamiltonian critical? BRUCITE, Mg(OH)2 Fundamental OH stretching frequencies, cm-1 Experiment B 3 LYP PW 91 LDA HF 3654 Experiment Δ 3325 4070 +9 -174 -329 +416 3654 B 3 LYP PBE 0 PBE-sol 3823 harmonic anharmonic 3480 Δ No hydrogen bond 3663 3698 3856 3622 3663 3526 3694 3447 +9 -128 +40 -207 Vallico Sotto July 2009 33

Is the choice of the Hamiltonian critical? Be(OH)2 Fundamental OD stretching frequencies. All data in cm-1 Experiment B 3 LYP Hydrogen bonded OH groups LDA HF 2468 2213 1757 2902 -98 2566 PW 91 -353 -809 +336 • Only B 3 LYP is in good agreement with experimental free OH frequency • All Hamiltonians are unable to predict shifts due to strong hydrogen bond • The 1 D approximation is not appropriated to describe the OH stretching properties in the case of strong interaction of the H atom (as HB). The anharmonic constant is overestimated. Vallico Sotto July 2009

Harmonic frequency in solids with CRYSTAL Building the Hessian matrix analytical first derivative numerical second derivative Harmonic frequencies at the central zone are obtained by diagonalising the mass weighted Hessian matrix, W Isotopic shift can be calculated at no cost! Vallico Sotto July 2009

The dynamical matrix The behavior of the phonons of a wave vector k close to the Γ point can be described as follows: Center-zone phonons: ANALYTICAL *greek indices: atoms in the primitive cell Dependence on the direction of k: limiting cases k→ 0 NON ANALYTICAL **latin indices: cartesian coordinates Vallico Sotto July 2009 36

The analytical part of the dynamical matrix *Mx= mass of the x atom **H=Hessian matrix Vallico Sotto July 2009

The Born charges The atomic Born tensors are the key quantities for : Ø calculation of the IR intensities Ø calculation of the static dielectric tensor Ø calculation of the Longitudinal Optical (LO) modes They are defined, in the cartesian basis, as: *Ei=component of an applied external field **μ=cell dipole moment Vallico Sotto July 2009

μ depends on the choice of the cell BUT the dipole moment difference between two geometries of the same periodic system (polarization per unit cell) is a defined observable. The partial second derivatives appearing in the Born tensors are estimated numerically from the polarizations generated by small atomic displacements (the same as for the second energy derivative) LOCALIZED WANNIER FUNCTIONS (WF) to compute polarization Vallico Sotto July 2009

Procedure for the polarization derivative calculation • full localization scheme for the equilibrium point → centroids of the resulting WFs • WFs of the central point are projected onto the corresponding occupied manifolds of the distorted structures → centroids of the resulting WFs • difference between the sum of the reference WF centroids at the two geometries • C. M. Zicovich-Wilson, R. Dovesi, V. R. Saunders A general method to obtain well localized Wannier functions for composite energy bands in linear combination of atomic orbital periodic calculations J. Chem. Phys. , 115, 9708 -9719 (2001) • Alternative scheme; through Berry phase • S. Dall’Olio, R. Dovesi, R. Resta Spontaneous polarization as a Berry phase of the HF wavefunction. Phys, Rev B 56, 10105 (1997) Vallico Sotto July 2009

The non-analytical contribution and the LO modes Dynamical matrix: matrix Analytical contribution: Non-analytical contribution: Vallico Sotto July 2009

Trasverse Optical (TO) modes: the non-analytic part vanishes K and Zp, m are perpendicular Longitudinal Optical (TO) modes: the non-analytic part is ≠ 0 K and Zp, m are parallel Vallico Sotto July 2009
CRYSTAL frequency calculation output Frequencies, symmetry analysys, IR intensities, IR and Raman activities Vallico Sotto July 2009

AIMS • Document the numerical stability of the computational process • Document the accuracy (with respect to experiment, when experiment is accurate) • Interpret the spectrum and attribute the modes Vallico Sotto July 2009 44
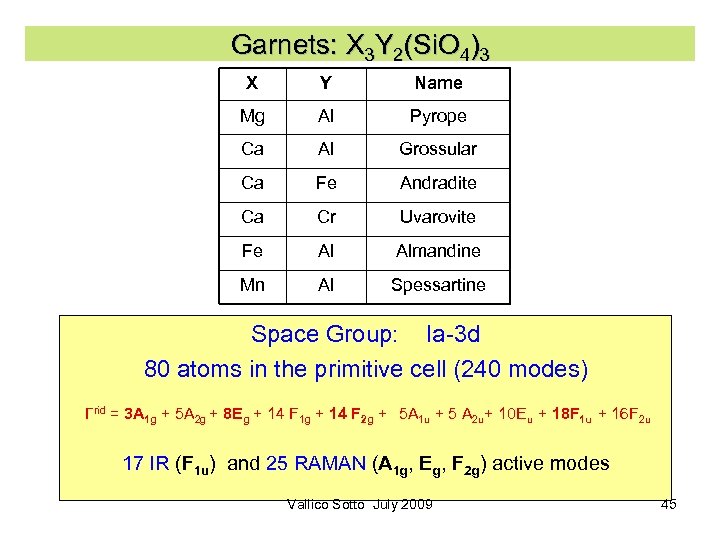
Garnets: X 3 Y 2(Si. O 4)3 X Y Name Mg Al Pyrope Ca Al Grossular Ca Fe Andradite Ca Cr Uvarovite Fe Al Almandine Mn Al Spessartine Space Group: Ia-3 d 80 atoms in the primitive cell (240 modes) Γrid = 3 A 1 g + 5 A 2 g + 8 Eg + 14 F 1 g + 14 F 2 g + 5 A 1 u + 5 A 2 u+ 10 Eu + 18 F 1 u + 16 F 2 u 17 IR (F 1 u) and 25 RAMAN (A 1 g, Eg, F 2 g) active modes Vallico Sotto July 2009 45
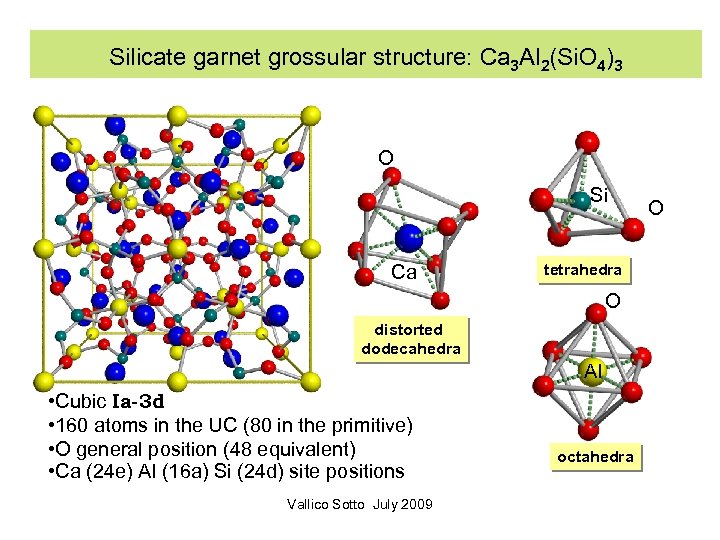
Silicate garnet grossular structure: Ca 3 Al 2(Si. O 4)3 O Si Ca tetrahedra O distorted dodecahedra Al • Cubic Ia-3 d • 160 atoms in the UC (80 in the primitive) • O general position (48 equivalent) • Ca (24 e) Al (16 a) Si (24 d) site positions Vallico Sotto July 2009 octahedra O

The interest for garnets+TM compounds • M. D. Towler, N. L. Allan, N. M. Harrison, V. R. Saunders, W. C. Mackrodt and E. Aprà An ab initio Hartree-Fock study of Mn. O and Ni. O. Phys. Rev. B 50, 5041 -5054 (1994) • R. Dovesi, J. M. Ricart, V. R. Saunders and R. Orlando Superexchange interaction in K 2 Ni. F 4. An ab initio Hartree-Fock study J. Phys. Cond. Matter 7, 7997 -8007 (1995) • Ph. D'Arco, F. Freyria Fava, R. Dovesi and V. R. Saunders Structural and electronic properties of Mg 3 Al 2 Si 3 O 12 pyrope garnet: an ab initio study J. Phys. : Cond. Matter 8, 8815 -8828 (1996) Vallico Sotto July 2009 47

Symmetry is crucial for solids R. Dovesi On the role of symmetry in the ab initio Hartree-Fock linear combination of atomic orbitals treatment of periodic systems. Int. J. Quantum Chem. 29, 1755 -1774 (1986). INTEGRALS C. Zicovich-Wilson and R. Dovesi, On the use of symmetry adapted crystalline orbitals in SCF-LCAO periodic calculations. I. The construction of the symmetrized orbitals. Int. J. Quantum Chem. 67, 299 -309 (1998). K SPACE DIAG-IRREPS C. Zicovich-Wilson and R. Dovesi, On the use of symmetry adapted crystalline orbitals in SCF-LCAO periodic calculations. II. Implementation of the Self-Consistent-Field Scheme and examples Int. J. Quantum Chem. 67, 311 -320 (1998). SYM LABELS TO STATES R. Dovesi, F. Pascale, C. M. Zicovich-Wilson The ab inizio calculation of the vibrational spectrum of cristalline compounds; the role of symmetry and related computational aspects. Beyond standard quantum chemistry: applications from gas to condensed phases ISBN: 978 -81 -7895 -293 -2 Editor: Ramon Hernandez-Lamoneda (2007) HESSIAN Vallico Sotto July 2009 48

Hessian construction and Symmetry (Garnet example) Each SCF+Gradient calculation provides one line of Hik 80 atoms = 240+1 SCF+G calculations with low (null) symmetry 1. Point symmetry is used to generate lines of atoms symmetry related 2. Other symmetries (among x, y, z lines; translational invariance) further reduce the number of required lines At the end only 9 out of 241 SCF+G calculations are required Vallico Sotto July 2009 49
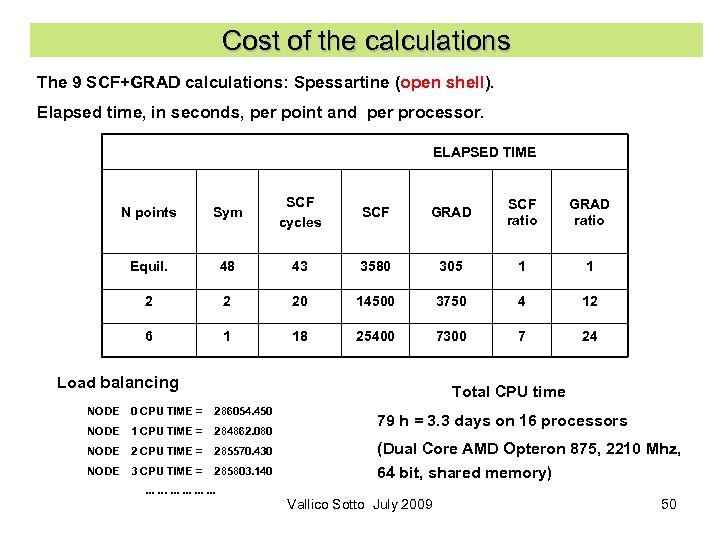
Cost of the calculations The 9 SCF+GRAD calculations: Spessartine (open shell). Elapsed time, in seconds, per point and per processor. ELAPSED TIME N points Sym SCF cycles SCF GRAD SCF ratio GRAD ratio Equil. 48 43 3580 305 1 1 2 2 20 14500 3750 4 12 6 1 18 25400 7300 7 24 Load balancing Total CPU time NODE 0 CPU TIME = 286054. 450 NODE 1 CPU TIME = 284862. 080 NODE 2 CPU TIME = 285570. 430 NODE 3 CPU TIME = 285803. 140 . . . . 79 h = 3. 3 days on 16 processors (Dual Core AMD Opteron 875, 2210 Mhz, 64 bit, shared memory) Vallico Sotto July 2009 50

Numerical stability of the computational process • DFT integration grid =0. 7 Large =0. 6 is the mean absolute deviation of frequencies between 2 values of the indicated option. (in cm-1) Standard XLarge Standard grid is enough (For the pyrope case) Grid (Rad, A ng) Standa rd (55, 434 ) Large (75, 974 ) XLarge (99, 145 4) • SCF convergence (total energy, in hartree) Tol∆E=10 -10 =0. 2 Tol∆E=10 -11 Vallico Sotto July 2009 51
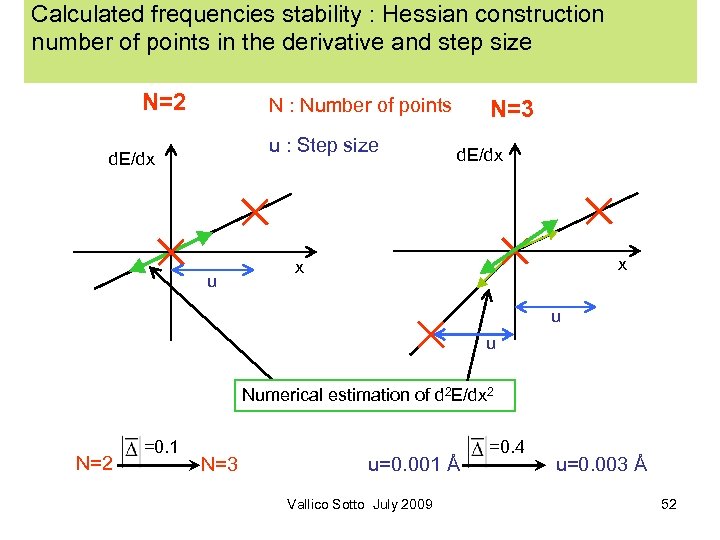
Calculated frequencies stability : Hessian construction number of points in the derivative and step size N=2 N : Number of points u : Step size d. E/dx u N=3 d. E/dx x x u u Numerical estimation of d 2 E/dx 2 N=2 =0. 1 N=3 u=0. 001 Å Vallico Sotto July 2009 =0. 4 u=0. 003 Å 52
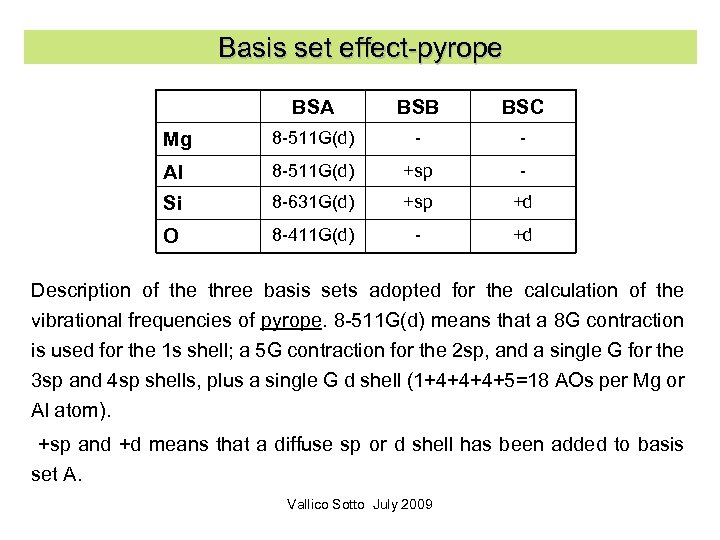
Basis set effect-pyrope BSA BSB BSC Mg 8 -511 G(d) - - Al 8 -511 G(d) +sp - Si 8 -631 G(d) +sp +d O 8 -411 G(d) - +d Description of the three basis sets adopted for the calculation of the vibrational frequencies of pyrope. 8 -511 G(d) means that a 8 G contraction is used for the 1 s shell; a 5 G contraction for the 2 sp, and a single G for the 3 sp and 4 sp shells, plus a single G d shell (1+4+4+4+5=18 AOs per Mg or Al atom). +sp and +d means that a diffuse sp or d shell has been added to basis set A. Vallico Sotto July 2009
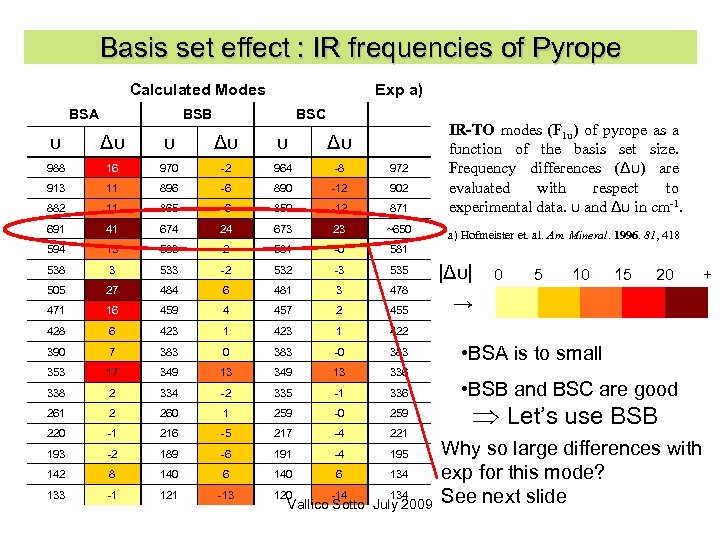
Basis set effect : IR frequencies of Pyrope Calculated Modes BSA Exp a) BSB BSC υ Δυ 988 16 970 -2 964 -8 972 913 11 896 -6 890 -12 902 882 11 865 -6 859 -12 871 691 41 674 24 673 23 ~650 594 13 583 2 581 -0 581 538 3 533 -2 532 -3 535 505 27 484 6 481 3 478 471 16 459 4 457 2 455 428 6 423 1 422 390 7 383 0 383 -0 383 353 17 349 13 336 338 2 334 -2 335 -1 336 261 2 260 1 259 -0 259 220 -1 216 -5 217 -4 221 193 -2 189 -6 191 -4 195 142 8 140 6 134 133 -1 121 -13 120 -14 134 IR-TO modes (F 1 u) of pyrope as a function of the basis set size. Frequency differences (Δυ) are evaluated with respect to experimental data. υ and Δυ in cm-1. Vallico Sotto July 2009 a) Hofmeister et. al. Am. Mineral. 1996. 81, 418 |Δυ| 0 5 10 15 20 + → • BSA is to small • BSB and BSC are good Let’s use BSB Why so large differences with exp for this mode? See next slide
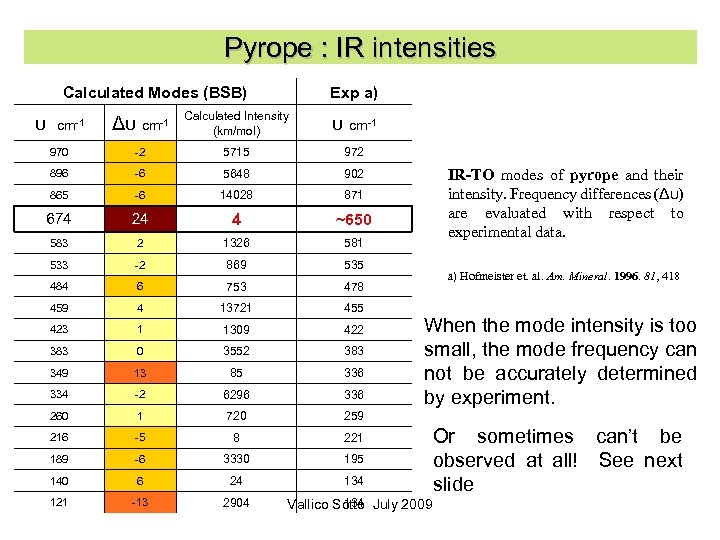
Pyrope : IR intensities Calculated Modes (BSB) Exp a) υ cm-1 Δυ cm-1 Calculated Intensity (km/mol) υ cm-1 970 -2 5715 972 896 -6 5648 902 865 -6 14028 871 674 24 4 ~650 583 2 1326 581 533 -2 869 535 484 6 753 478 459 4 13721 455 423 1 1309 422 383 0 3552 383 349 13 85 336 334 -2 6296 336 260 1 720 259 216 -5 8 221 189 -6 3330 195 140 6 24 134 121 -13 2904 IR-TO modes of pyrope and their intensity. Frequency differences (Δυ) are evaluated with respect to experimental data. a) Hofmeister et. al. Am. Mineral. 1996. 81, 418 When the mode intensity is too small, the mode frequency can not be accurately determined by experiment. 134 Vallico Sotto July 2009 Or sometimes can’t be observed at all! See next slide
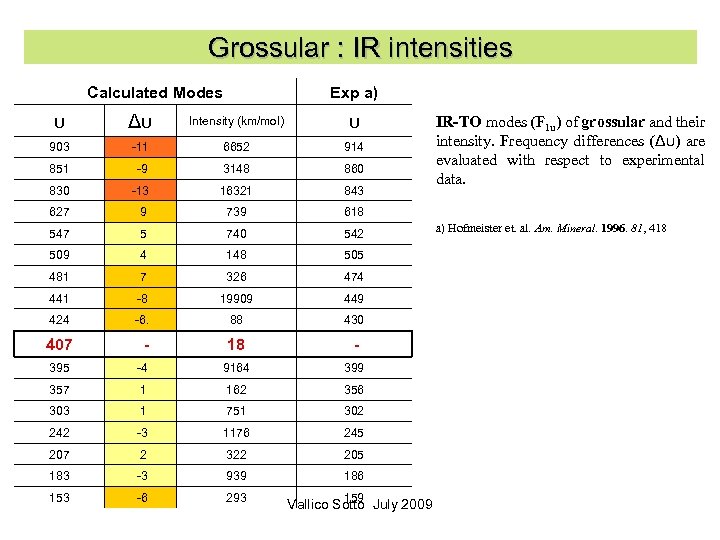
Grossular : IR intensities Calculated Modes Exp a) υ Δυ Intensity (km/mol) υ 903 -11 6652 914 851 -9 3148 860 830 -13 16321 843 627 9 739 618 547 5 740 542 509 4 148 505 481 7 326 474 441 -8 19909 449 424 -6. 88 430 407 - 18 - 395 -4 9164 399 357 1 162 356 303 1 751 302 242 -3 1176 245 207 2 322 205 183 -3 939 186 153 -6 293 159 Vallico Sotto July 2009 IR-TO modes (F 1 u) of grossular and their intensity. Frequency differences (Δυ) are evaluated with respect to experimental data. a) Hofmeister et. al. Am. Mineral. 1996. 81, 418
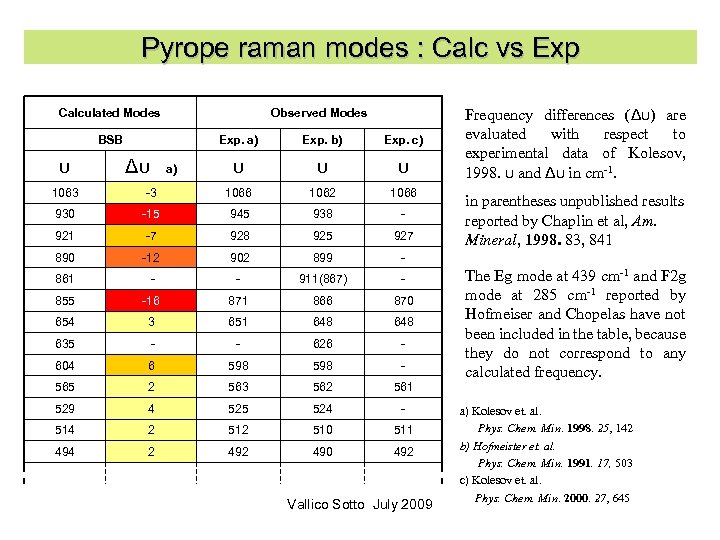
Pyrope raman modes : Calc vs Exp Calculated Modes BSB Observed Modes Exp. a) Exp. b) Exp. c) υ Δυ a) υ υ υ 1063 -3 1066 1062 1066 930 -15 945 938 - 921 -7 928 925 927 890 -12 902 899 - 861 - - 911(867) - 855 -16 871 866 870 654 3 651 648 635 - - 626 - 604 6 598 - 565 2 563 562 561 529 4 525 524 - 514 2 510 511 494 2 490 492 Frequency differences (Δυ) are evaluated with respect to experimental data of Kolesov, 1998. υ and Δυ in cm-1. Vallico Sotto July 2009 in parentheses unpublished results reported by Chaplin et al, Am. Mineral, 1998. 83, 841 The Eg mode at 439 cm-1 and F 2 g mode at 285 cm-1 reported by Hofmeiser and Chopelas have not been included in the table, because they do not correspond to any calculated frequency. a) Kolesov et. al. Phys. Chem. Min. 1998. 25, 142 b) Hofmeister et. al. Phys. Chem. Min. 1991. 17, 503 c) Kolesov et. al. Phys. Chem. Min. 2000. 27, 645
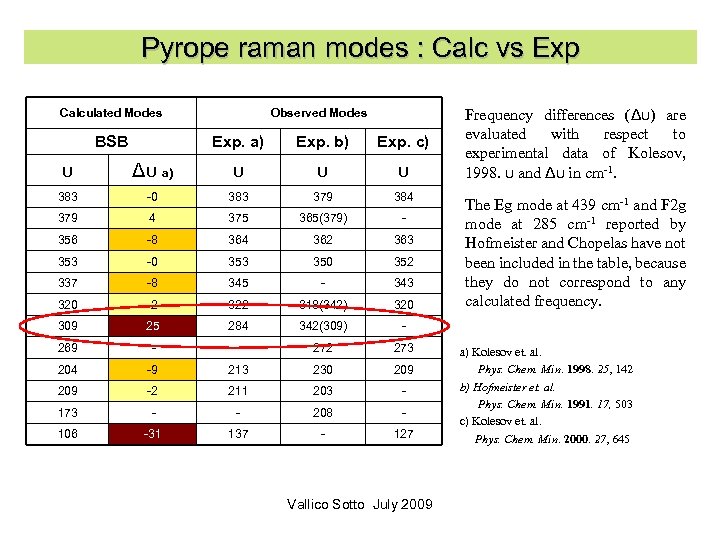
Pyrope raman modes : Calc vs Exp Calculated Modes BSB Observed Modes Exp. a) Exp. b) Exp. c) υ Δυ a) υ υ υ 383 -0 383 379 384 379 4 375 365(379) - 356 -8 364 362 363 353 -0 353 350 352 337 -8 345 - 343 320 -2 322 318(342) 320 309 25 284 342(309) - 269 - - 272 273 204 -9 213 230 209 -2 211 203 - 173 - - 208 - 106 -31 137 - 127 Frequency differences (Δυ) are evaluated with respect to experimental data of Kolesov, 1998. υ and Δυ in cm-1. Vallico Sotto July 2009 The Eg mode at 439 cm-1 and F 2 g mode at 285 cm-1 reported by Hofmeister and Chopelas have not been included in the table, because they do not correspond to any calculated frequency. a) Kolesov et. al. Phys. Chem. Min. 1998. 25, 142 b) Hofmeister et. al. Phys. Chem. Min. 1991. 17, 503 c) Kolesov et. al. Phys. Chem. Min. 2000. 27, 645
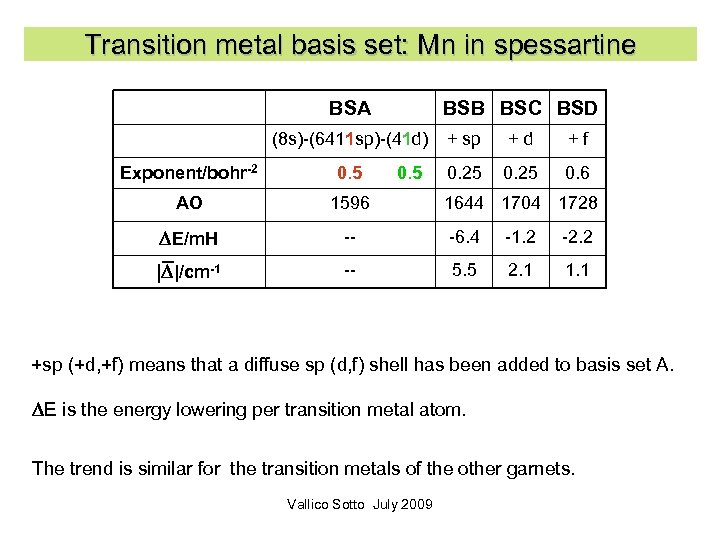
Transition metal basis set: Mn in spessartine BSA (8 s)-(6411 sp)-(41 d) Exponent/bohr-2 0. 5 BSB BSC BSD + sp + d + f 0. 25 0. 6 AO 1596 1644 1704 1728 DE/m. H -- -6. 4 -1. 2 -2. 2 |D|/cm-1 -- 5. 5 2. 1 1. 1 +sp (+d, +f) means that a diffuse sp (d, f) shell has been added to basis set A. DE is the energy lowering per transition metal atom. The trend is similar for the transition metals of the other garnets. Vallico Sotto July 2009
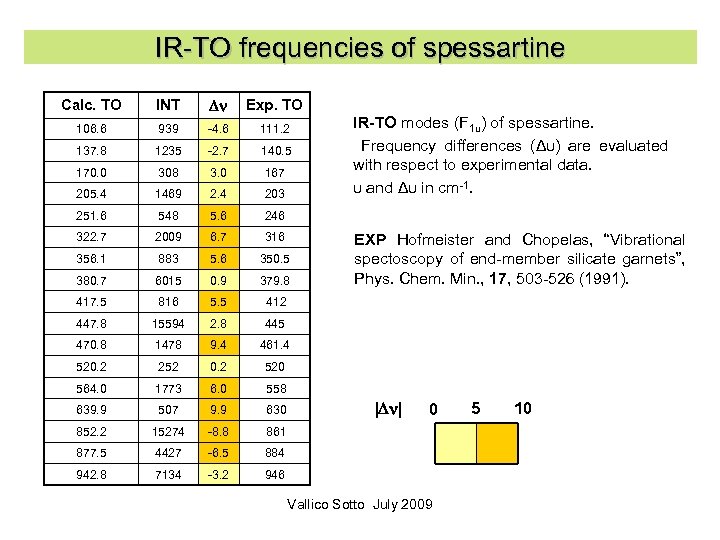
IR-TO frequencies of spessartine Calc. TO INT Dn Exp. TO 106. 6 939 -4. 6 111. 2 137. 8 1235 -2. 7 140. 5 170. 0 308 3. 0 167 205. 4 1469 2. 4 203 251. 6 548 5. 6 246 322. 7 2009 6. 7 316 356. 1 883 5. 6 350. 5 380. 7 6015 0. 9 379. 8 417. 5 816 5. 5 412 447. 8 15594 2. 8 445 470. 8 1478 9. 4 461. 4 520. 2 252 0. 2 520 564. 0 1773 6. 0 558 639. 9 507 9. 9 630 852. 2 15274 -8. 8 861 877. 5 4427 -6. 5 884 942. 8 7134 -3. 2 946 IR-TO modes (F 1 u) of spessartine. Frequency differences (Δυ) are evaluated with respect to experimental data. υ and Δυ in cm-1. EXP Hofmeister and Chopelas, “Vibrational spectoscopy of end-member silicate garnets”, Phys. Chem. Min. , 17, 503 -526 (1991). |Dn| 0 Vallico Sotto July 2009 5 10
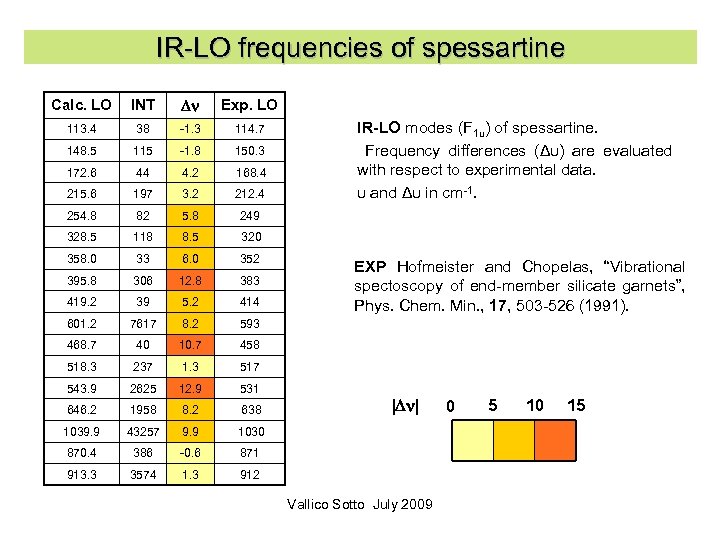
IR-LO frequencies of spessartine Calc. LO INT Dn Exp. LO 113. 4 38 -1. 3 114. 7 148. 5 115 -1. 8 150. 3 172. 6 44 4. 2 168. 4 215. 6 197 3. 2 212. 4 254. 8 82 5. 8 249 328. 5 118 8. 5 320 358. 0 33 6. 0 352 395. 8 306 12. 8 383 419. 2 39 5. 2 414 601. 2 7617 8. 2 593 468. 7 40 10. 7 458 518. 3 237 1. 3 517 543. 9 2625 12. 9 531 646. 2 1958 8. 2 638 1039. 9 43257 9. 9 1030 870. 4 386 -0. 6 871 913. 3 3574 1. 3 912 IR-LO modes (F 1 u) of spessartine. Frequency differences (Δυ) are evaluated with respect to experimental data. υ and Δυ in cm-1. EXP Hofmeister and Chopelas, “Vibrational spectoscopy of end-member silicate garnets”, Phys. Chem. Min. , 17, 503 -526 (1991). |Dn| Vallico Sotto July 2009 0 5 10 15
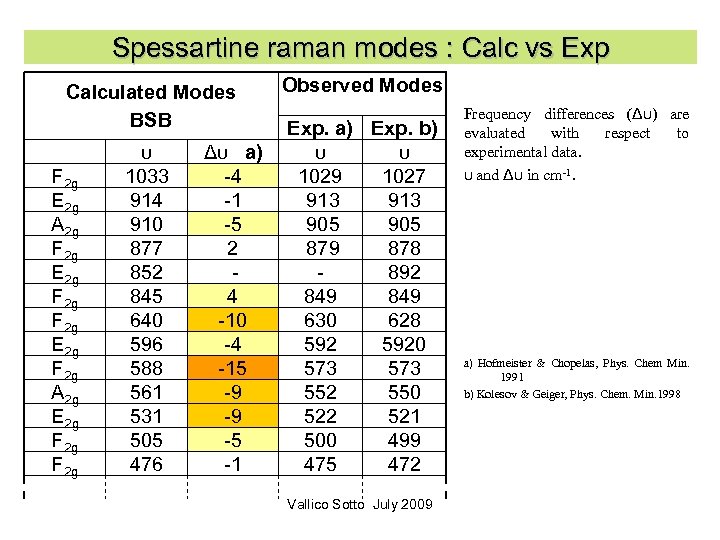
Spessartine raman modes : Calc vs Exp Calculated Modes BSB F 2 g E 2 g A 2 g F 2 g E 2 g F 2 g A 2 g E 2 g F 2 g υ 1033 914 910 877 852 845 640 596 588 561 531 505 476 Δυ a) -4 -1 -5 2 4 -10 -4 -15 -9 -9 -5 -1 Observed Modes Exp. a) Exp. b) υ υ 1029 1027 913 905 879 878 892 849 630 628 5920 573 552 550 522 521 500 499 475 472 Vallico Sotto July 2009 Frequency differences (Δυ) are evaluated with respect to experimental data. υ and Δυ in cm-1. a) Hofmeister & Chopelas, Phys. Chem Min. 1991 b) Kolesov & Geiger, Phys. Chem. Min. 1998
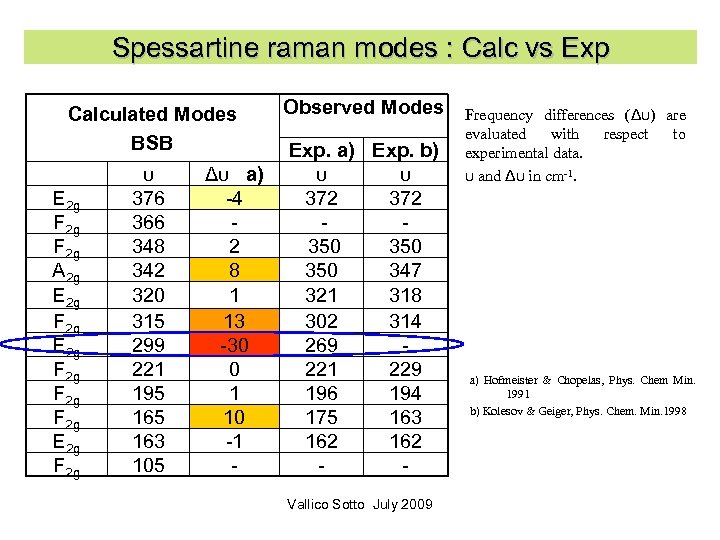
Spessartine raman modes : Calc vs Exp Calculated Modes BSB E 2 g F 2 g A 2 g E 2 g F 2 g E 2 g F 2 g υ 376 366 348 342 320 315 299 221 195 163 105 Δυ a) -4 2 8 1 13 -30 0 1 10 -1 - Observed Modes Exp. a) Exp. b) υ υ 372 350 350 347 321 318 302 314 269 221 229 196 194 175 163 162 Vallico Sotto July 2009 Frequency differences (Δυ) are evaluated with respect to experimental data. υ and Δυ in cm-1. a) Hofmeister & Chopelas, Phys. Chem Min. 1991 b) Kolesov & Geiger, Phys. Chem. Min. 1998
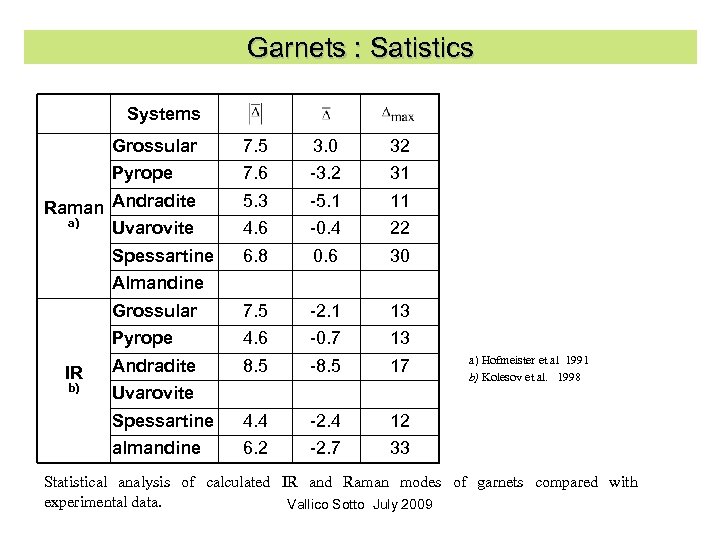
Garnets : Satistics Systems Grossular 7. 5 3. 0 32 Pyrope 7. 6 -3. 2 31 5. 3 -5. 1 11 4. 6 -0. 4 22 6. 8 0. 6 30 Grossular 7. 5 -2. 1 13 Pyrope 4. 6 -0. 7 13 Andradite 8. 5 -8. 5 17 Spessartine 4. 4 -2. 4 12 almandine 6. 2 -2. 7 33 Raman Andradite a) Uvarovite Spessartine Almandine IR b) Uvarovite a) Hofmeister et al 1991 b) Kolesov et al. 1998 Statistical analysis of calculated IR and Raman modes of garnets compared with experimental data. Vallico Sotto July 2009

The isotopic shift • As a tool for the assignement of the modes and for the interpretation of the spectrum. • Each atom at a time • In some cases also infinite mass Vallico Sotto July 2009 66
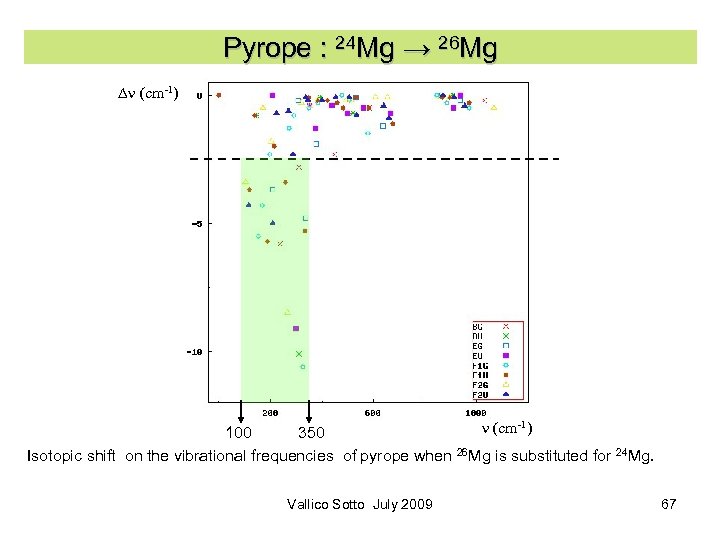
Pyrope : 24 Mg → 26 Mg Dn (cm-1) 100 350 Isotopic shift on the vibrational frequencies of pyrope when 26 Mg is substituted for 24 Mg. Vallico Sotto July 2009 67
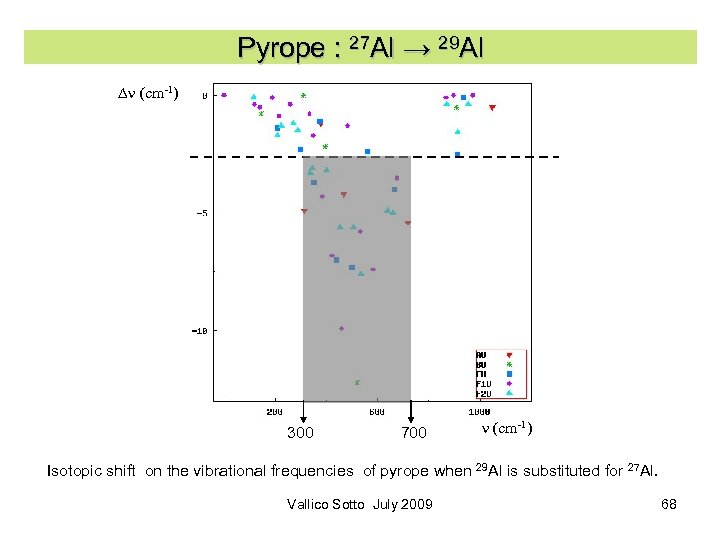
Pyrope : 27 Al → 29 Al Dn (cm-1) 300 700 n (cm-1) Isotopic shift on the vibrational frequencies of pyrope when 29 Al is substituted for 27 Al. Vallico Sotto July 2009 68
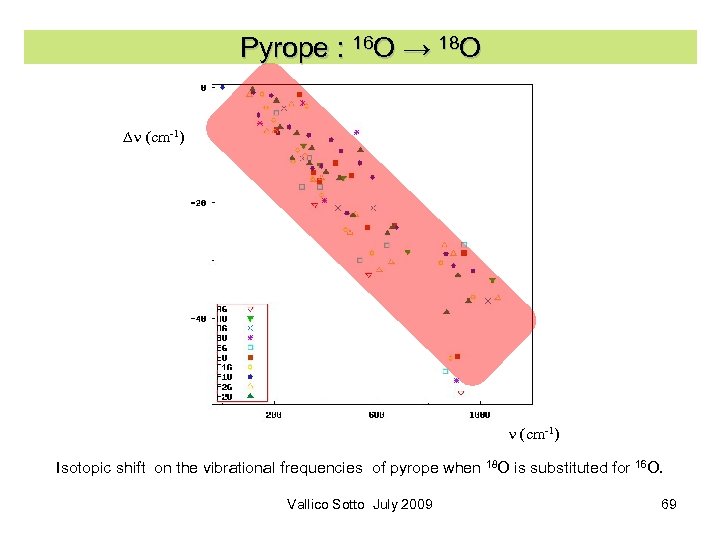
Pyrope : 16 O → 18 O Dn (cm-1) Isotopic shift on the vibrational frequencies of pyrope when 18 O is substituted for 16 O. Vallico Sotto July 2009 69
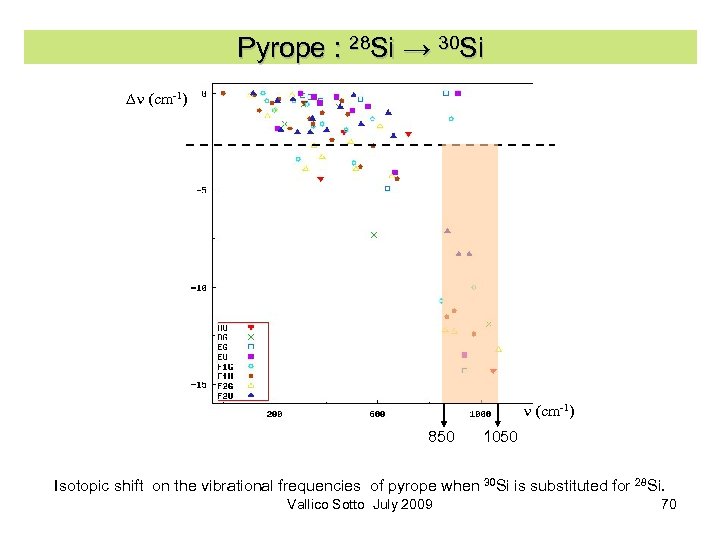
Pyrope : 28 Si → 30 Si Dn (cm-1) 850 1050 Isotopic shift on the vibrational frequencies of pyrope when 30 Si is substituted for 28 Si. Vallico Sotto July 2009 70

Internal/external modes Si-O bonds stronger than the others Modes separated in 2 types: • Internal modes (deformation of the tetrahedra) • External modes (solid tetrahedra) Vallico Sotto July 2009 71
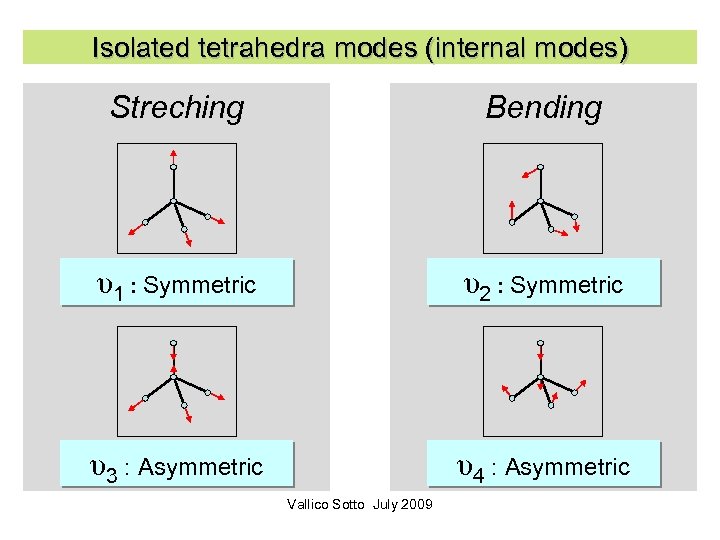
Isolated tetrahedra modes (internal modes) Streching Bending υ1 : Symmetric υ2 : Symmetric υ3 : Asymmetric υ4 : Asymmetric Vallico Sotto July 2009
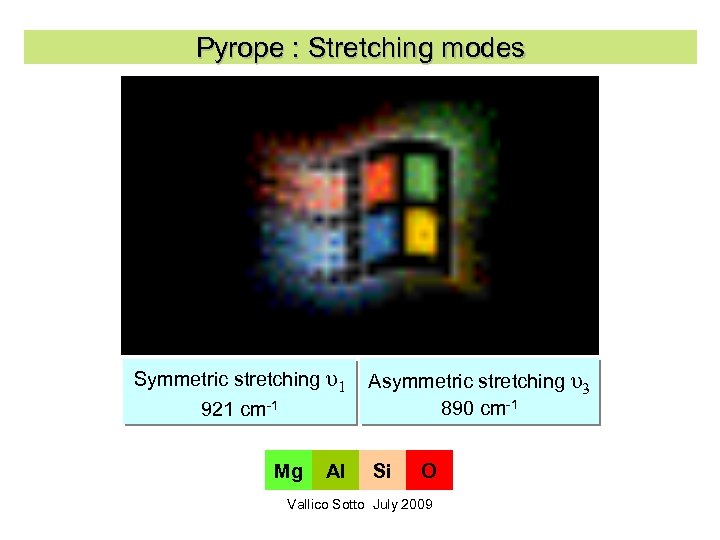
Pyrope : Stretching modes Symmetric stretching υ1 921 cm-1 Mg Al Asymmetric stretching υ3 890 cm-1 Si O Vallico Sotto July 2009
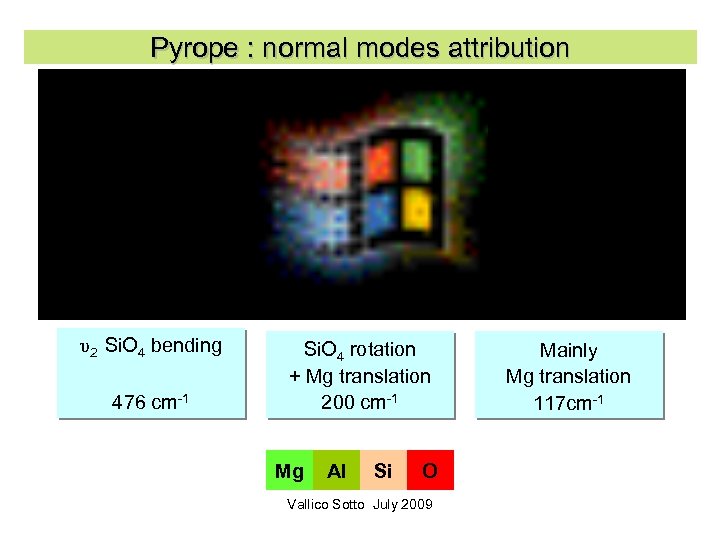
Pyrope : normal modes attribution υ2 Si. O 4 bending 476 cm-1 Si. O 4 rotation + Mg translation 200 cm-1 Mg Al Si O Vallico Sotto July 2009 Mainly Mg translation 117 cm-1

The problem of H It is well known that the stretching modes involving hydrogen atoms are strongly anharmonic: typically for the O-H stretching anharmonicity can be as large as 180 cm-1. However this difficulty is compensated by the full separability of this mode. Vallico Sotto July 2009 75
Anharmonic correction for hydroxyls exe=(2 01 - 02) / 2 OH stretching is considered as decoupled from any other normal modes E 2 E 1 E 0 A wide range (0. 5 Å) of OH distances must be explored to properly evaluate E 1 and E 2 02 01 This procedure is automatically implemented in the code Direct comparison with experiment for fundamental frequency, first overtone and anharmonicity constant Vallico Sotto July 2009
Isolated OH groups in crystals: model structures/1 H O M Edingtonite surface Chabazite M=Mg Brucite M=Ca Portlandite All calculations with 6 -31 G(d, p) basis set Vallico Sotto July 2009

B 3 LYP vs experimental OH frequencies Vallico Sotto July 2009
Is the choice of the Hamiltonian critical? BRUCITE, Mg(OH)2 Fundamental OH stretching frequencies, cm-1 Experiment B 3 LYP PW 91 LDA HF 3654 Experiment Δ 3325 4070 +9 -174 -329 +416 3654 B 3 LYP PBE 0 PBE-sol 3823 harmonic anharmonic 3480 Δ No hydrogen bond 3663 3698 3856 3622 3663 3526 3694 3447 +9 -128 +40 -207 Vallico Sotto July 2009 79

Is the choice of the Hamiltonian critical? Be(OH)2 Fundamental OD stretching frequencies. All data in cm-1 Experiment B 3 LYP Hydrogen bonded OH groups LDA HF 2468 2213 1757 2902 -98 2566 PW 91 -353 -809 +336 • Only B 3 LYP is in good agreement with experimental free OH frequency • All Hamiltonians are unable to predict shifts due to strong hydrogen bond • The 1 D approximation is not appropriated to describe the OH stretching properties in the case of strong interaction of the H atom (as HB). The anharmonic constant is overestimated. Vallico Sotto July 2009
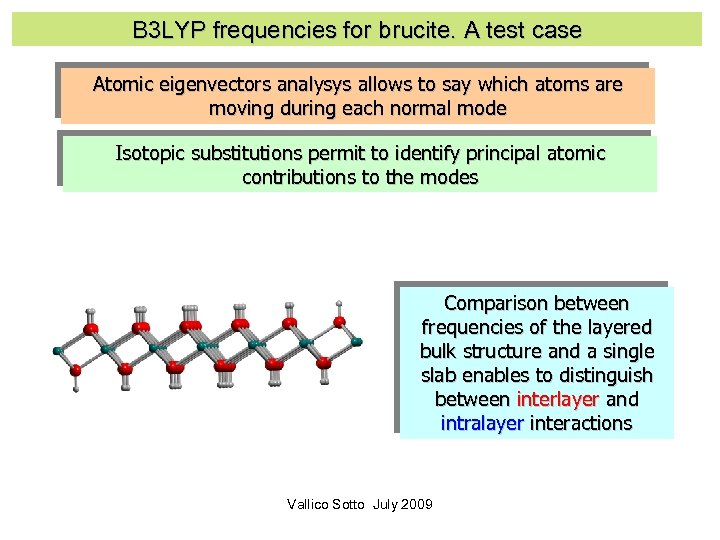
B 3 LYP frequencies for brucite. A test case Atomic eigenvectors analysys allows to say which atoms are moving during each normal mode Isotopic substitutions permit to identify principal atomic contributions to the modes Comparison between frequencies of the layered bulk structure and a single slab enables to distinguish between interlayer and intralayer interactions Vallico Sotto July 2009
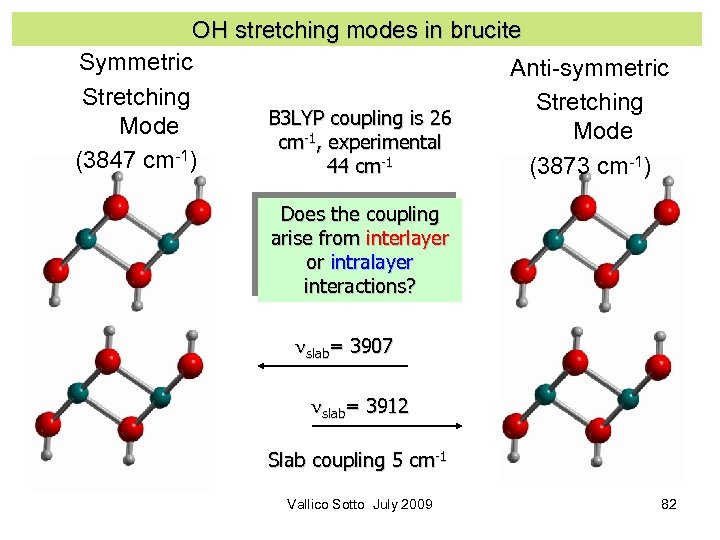
OH stretching modes in brucite Symmetric Anti-symmetric Stretching B 3 LYP coupling is 26 Mode cm-1, experimental (3847 cm-1) 44 cm-1 (3873 cm-1) Does the coupling arise from interlayer or intralayer interactions? nslab= 3907 nslab= 3912 Slab coupling 5 cm-1 Vallico Sotto July 2009 82
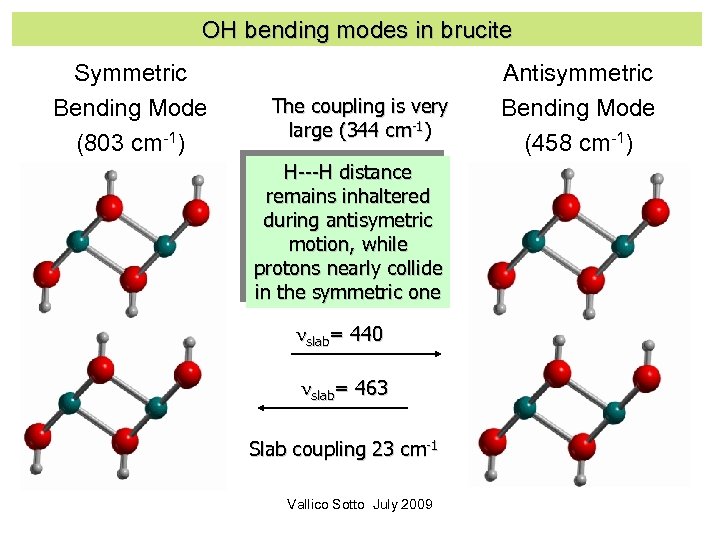
OH bending modes in brucite Symmetric Bending Mode (803 cm-1) The coupling is very large (344 cm-1) H---H distance remains inhaltered during antisymetric motion, while protons nearly collide in the symmetric one nslab= 440 nslab= 463 Slab coupling 23 cm-1 Vallico Sotto July 2009 Antisymmetric Bending Mode (458 cm-1)
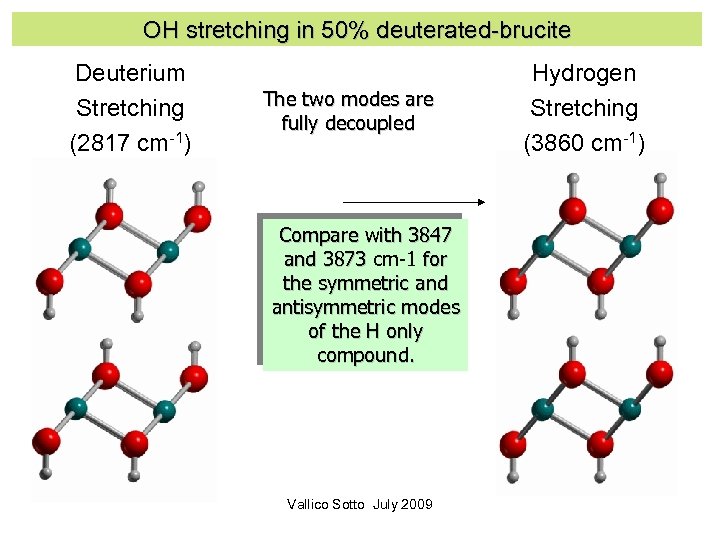
OH stretching in 50% deuterated-brucite Deuterium Stretching (2817 cm-1) The two modes are fully decoupled Compare with 3847 and 3873 cm-1 for the symmetric and antisymmetric modes of the H only compound. Vallico Sotto July 2009 Hydrogen Stretching (3860 cm-1)
8b0d1f2a6a70d51d965f15a25edd119f.ppt