fafb137e3a2a62c3cd4057029e8fa956.ppt
- Количество слайдов: 65

B 280 F Introduction to Financial Management Lecture 5 Risk and Rates of Return

Objectives n Inflation and rates of return n How to measure risk (variance, standard deviation, beta) n How to reduce risk (diversification) n How to price risk (security market line, Capital Asset Pricing Model) 2

Interest Rates Conceptually: Nominal risk-free Interest Rate = Real risk-free Interest Rate krf k* + Inflation risk premium IRP Mathematically: (1 + krf) = (1 + k*) (1 + IRP) This is known as the “Fisher Effect” 3

Interest Rates n Suppose the real rate is 3%, and the nominal rate is 8%. What is the inflation risk premium? (1 + krf) = (1 + k*) (1 + IRP) (1. 08) = (1. 03) (1 + IRP) = (1. 0485), so IRP = 4. 85% 4
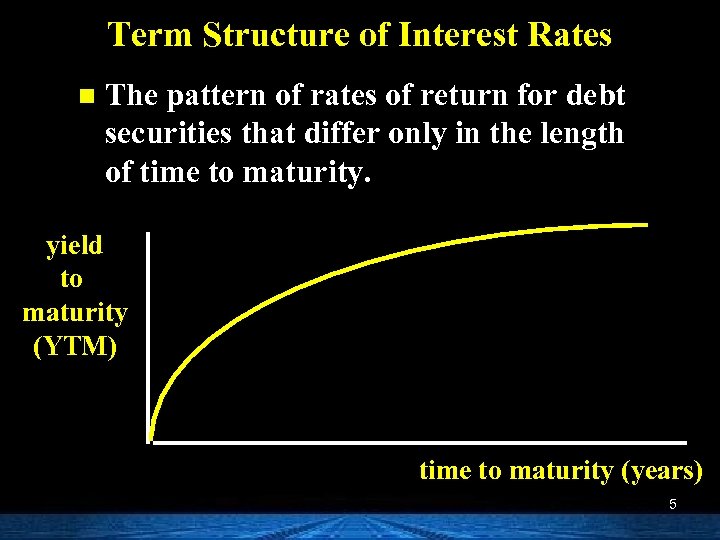
Term Structure of Interest Rates n The pattern of rates of return for debt securities that differ only in the length of time to maturity. yield to maturity (YTM) time to maturity (years) 5
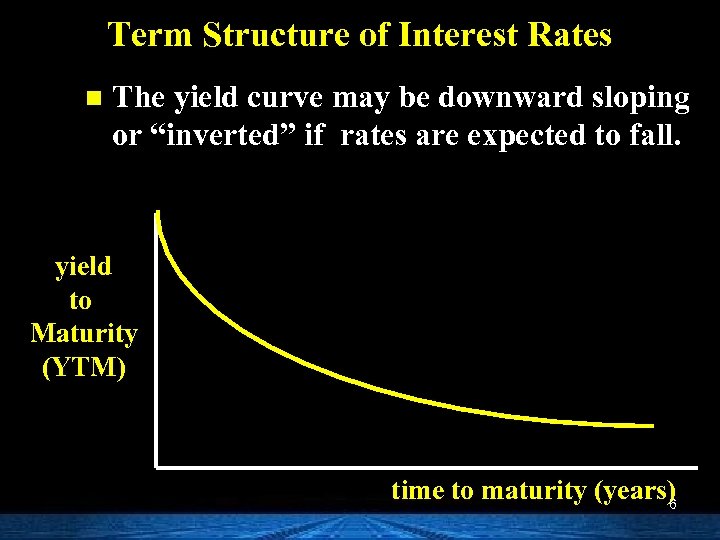
Term Structure of Interest Rates n The yield curve may be downward sloping or “inverted” if rates are expected to fall. yield to Maturity (YTM) time to maturity (years) 6

For a Treasury security, what is the required rate of return? Required rate of return = Risk-free rate of return Since Treasuries are essentially free of default risk, the rate of return on a Treasury security is considered the “risk -free” rate of return. 7

For a corporate stock or bond, what is the required rate of return? Required rate of return = Risk-free rate of return + Risk premium How large of a risk premium should we require to buy a corporate security? 8

Returns n Expected Rate of Return - the return that an investor expects to earn on an asset, given its price, growth potential, etc. n Required Rate of Return - the return that an investor requires on an asset given its risk and market interest rates. 9

Expected Return State of Probability Return Economy (P) Orl. Utility Orl. Tech Recession. 20 4% -10% Normal. 50 10% 14% Boom. 30 14% 30% For each firm, the expected return on the stock is just a weighted average: k = P(k 1)*k 1 + P(k 2)*k 2 +. . . + P(kn)*kn 10

Expected Return State of Probability Return Economy (P) Orl. Utility Orl. Tech Recession. 20 4% -10% Normal. 50 10% 14% Boom. 30 14% 30% k = P(k 1)*k 1 + P(k 2)*k 2 +. . . + P(kn)*kn k (OU) =. 2 (4%) +. 5 (10%) +. 3 (14%) = 10% 11

Expected Return State of Probability Return Economy (P) Orl. Utility Orl. Tech Recession. 20 4% -10% Normal. 50 10% 14% Boom. 30 14% 30% k = P(k 1)*k 1 + P(k 2)*k 2 +. . . + P(kn)*kn k (OT) =. 2 (-10%)+. 5 (14%) +. 3 (30%) = 14% 12

Portfolio Expected Returns n Weighted average of the expected return of each individual stock with the weights being equal to the proportion of the portfolio invested in each security 13

Portfolio Expected Returns n Assume you wish to hold a portfolio consisting of asset A and a riskless asset. Given the following information, calculate portfolio expected returns and portfolio betas, letting the proportion of funds invested in asset A range from 0 to 125%. Asset A has an expected return of 18%. The risk-free rate is 7%. Asset A weights: 0%, 25%, 50%, 75%, 100%, and 125%. 14
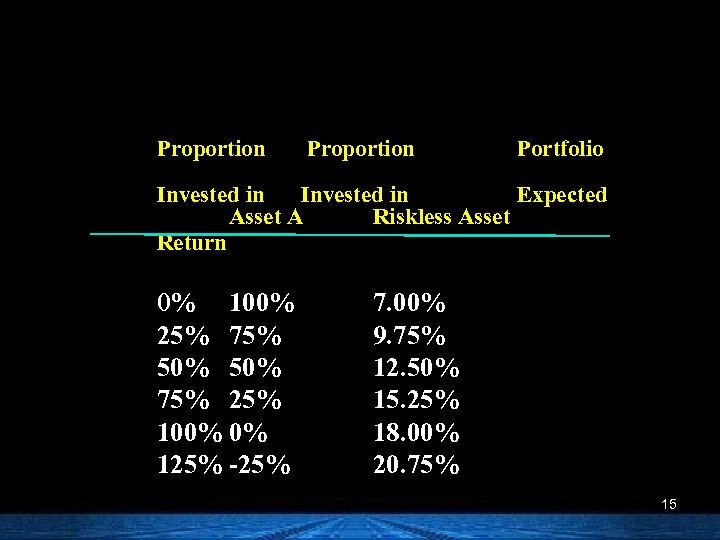
Proportion Portfolio Invested in Expected Asset A Riskless Asset Return 0% 100% 25% 75% 50% 75% 25% 100% 0% 125% -25% 7. 00% 9. 75% 12. 50% 15. 25% 18. 00% 20. 75% 15

Holding Period Return Calculations $50 $60 t t+1 Pt+1 - Pt Pt Pt+1 Pt = -1 = 60 - 50 50 60 50 = 20% -1 = 20% 16
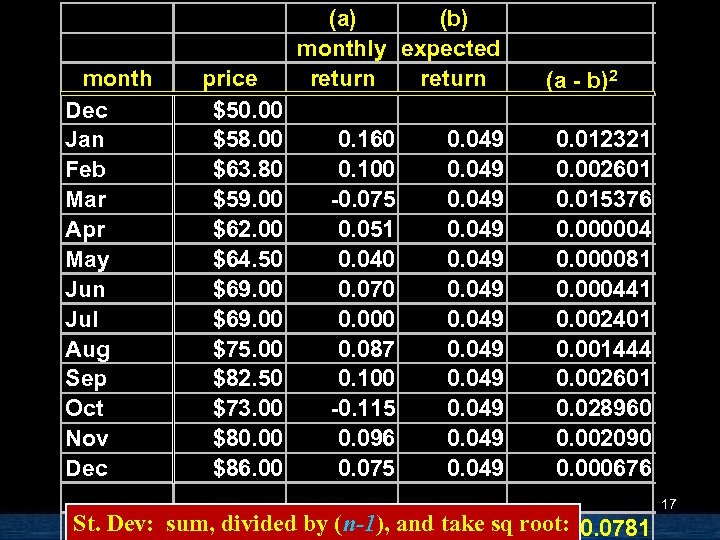
month Dec Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec price $50. 00 $58. 00 $63. 80 $59. 00 $62. 00 $64. 50 $69. 00 $75. 00 $82. 50 $73. 00 $80. 00 $86. 00 (a) (b) monthly expected return 0. 160 0. 100 -0. 075 0. 051 0. 040 0. 070 0. 000 0. 087 0. 100 -0. 115 0. 096 0. 075 0. 049 0. 049 (a - b)2 0. 012321 0. 002601 0. 015376 0. 000004 0. 000081 0. 000441 0. 002401 0. 001444 0. 002601 0. 028960 0. 002090 0. 000676 St. Dev: sum, divided by (n-1), and take sq root: 0. 0781 17

What is Risk? n The possibility that an actual return will differ from our expected return. n Uncertainty in the distribution of possible outcomes. 18

What is Risk? n Uncertainty in the distribution of possible outcomes. Company A Company B return 19

How do We Measure Risk? n To get a general idea of a stock’s price variability, we could look at the stock’s price range over the past year. 52 weeks Yld Vol Net Hi Lo Sym Div % PE 100 s Hi Lo Close Chg 134 80 IBM. 52. 5 21 143402 98 95 9549 -3 115 40 MSFT … 29 558918 55 52 5194 -475 20

How do We Measure Risk? n A more scientific approach is to examine the stock’s standard deviation of returns. n Standard deviation is a measure of the dispersion of possible outcomes. n The greater the standard deviation, the greater the uncertainty, and, therefore, the greater the risk. 21

Standard Deviation s = n S i=1 (ki - 2 k) P(ki) 22

s= n S (k i=1 i 2 k) P(ki) Orlando Utility, Inc. ( 4% - 10%)2 (. 2) = 7. 2 (10% - 10%)2 (. 5) = 0 (14% - 10%)2 (. 3) = 4. 8 Variance = 12 Stand. dev. = 12 = 3. 46% 23

s= n S (k i=1 i 2 k) P(ki) Orlando Technology, Inc. (-10% - 14%)2 (. 2) = 115. 2 (14% - 14%)2 (. 5) = 0 (30% - 14%)2 (. 3) = 76. 8 Variance = 192 Stand. dev. = 192 = 13. 86% 24

Which stock would you prefer? How would you decide? 25
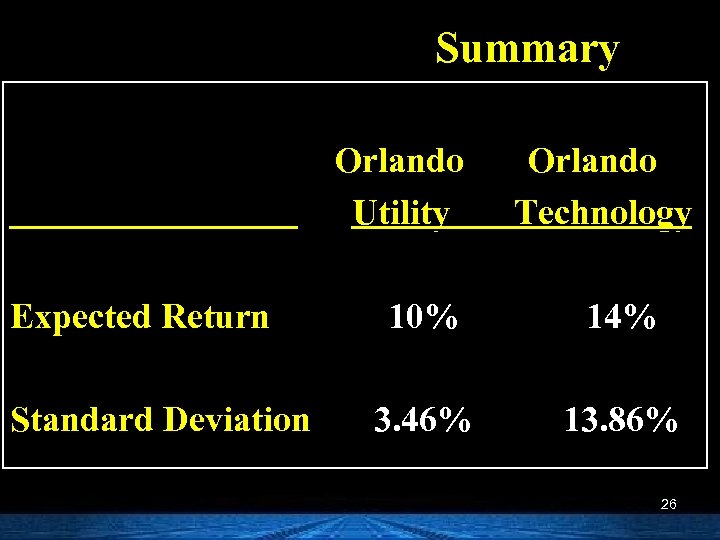
Summary Orlando Utility Expected Return Standard Deviation Orlando Technology 10% 14% 3. 46% 13. 86% 26
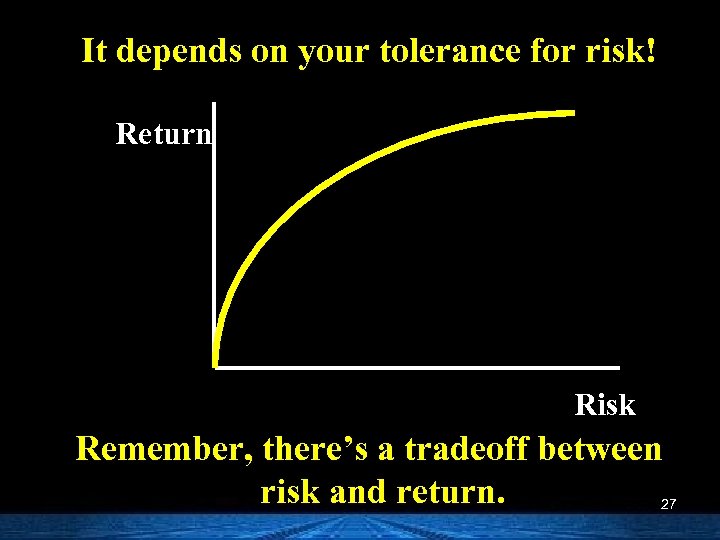
It depends on your tolerance for risk! Return Risk Remember, there’s a tradeoff between risk and return. 27

Portfolios n Combining several securities in a portfolio can actually reduce overall risk. n How does this work? 28
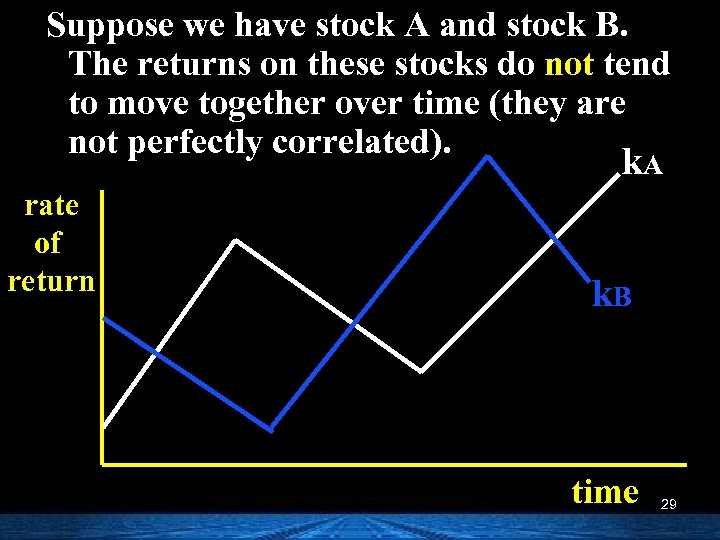
Suppose we have stock A and stock B. The returns on these stocks do not tend to move together over time (they are not perfectly correlated). k. A rate of return k. B time 29
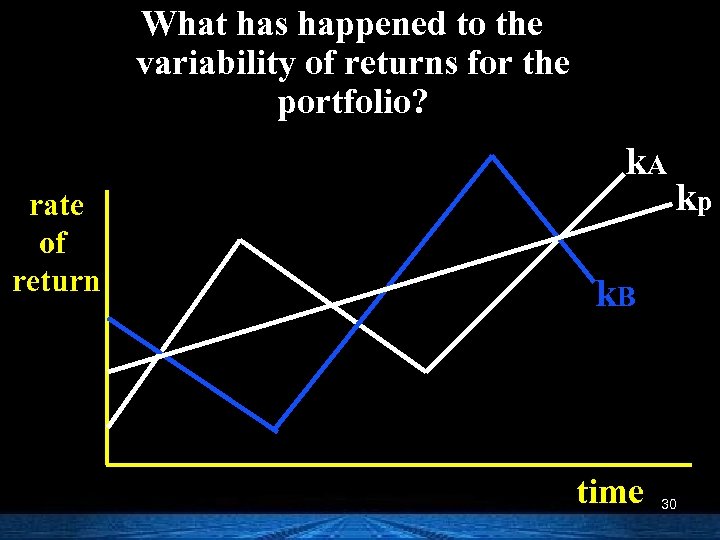
What has happened to the variability of returns for the portfolio? k. A rate of return kp k. B time 30

Diversification n Investing in more than one security to reduce risk. n If two stocks are perfectly positively correlated, diversification has no effect on risk. n If two stocks are perfectly negatively correlated, the portfolio is perfectly diversified. 31

n If you owned a share of every stock traded on the NYSE and NASDAQ, would you be diversified? YES! n Would you have eliminated all of your risk? NO! Common stock portfolios still have risk. 32

Some risk can be diversified away and some cannot. n Market risk (systematic risk) is nondiversifiable. This type of risk cannot be diversified away. n Company-unique risk (unsystematic risk) is diversifiable. This type of risk can be reduced through diversification. 33

Market Risk n Unexpected changes in interest rates. n Unexpected changes in cash flows due to tax rate changes, foreign competition, and the overall business cycle. 34

Company-unique Risk n A company’s labor force goes on strike. n A company’s top management dies in a plane crash. n A huge oil tank bursts and floods a company’s production area. 35
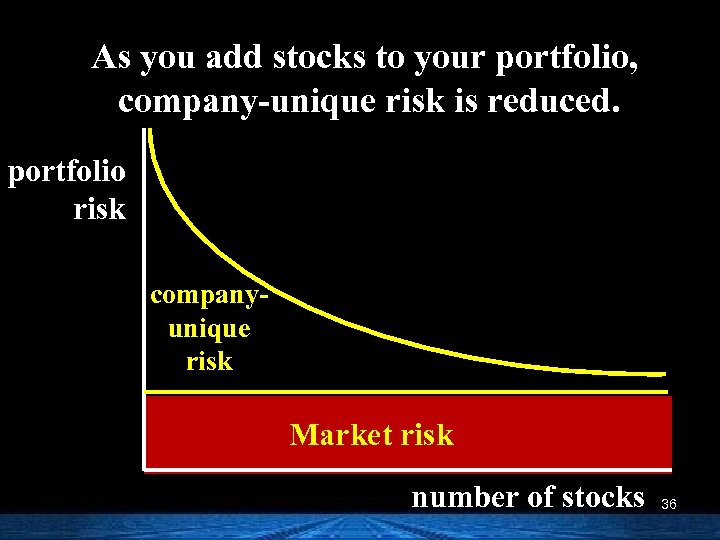
As you add stocks to your portfolio, company-unique risk is reduced. portfolio risk companyunique risk Market risk number of stocks 36

Do some firms have more market risk than others? Yes. For example: Interest rate changes affect all firms, but which of the following would be more affected? a) Retail food chain b) Commercial bank 37

n Note As we know, the market compensates investors for accepting risk - but only for market risk. Companyunique risk can and should be diversified away. So - we need to be able to measure market risk. 38

This is why we have Beta: a measure of market risk. n Specifically, beta is a measure of how an individual stock’s returns vary with market returns. n It’s a measure of the “sensitivity” of an individual stock’s returns to changes in the market. 39

The market’s beta is 1 A firm that has a beta = 1 has average market risk. The stock is as volatile as the market. n A firm with a beta > 1 is more volatile than the market. – (ex: technology firms) n A firm with a beta < 1 is less volatile than the market. – (ex: utilities) 40 n
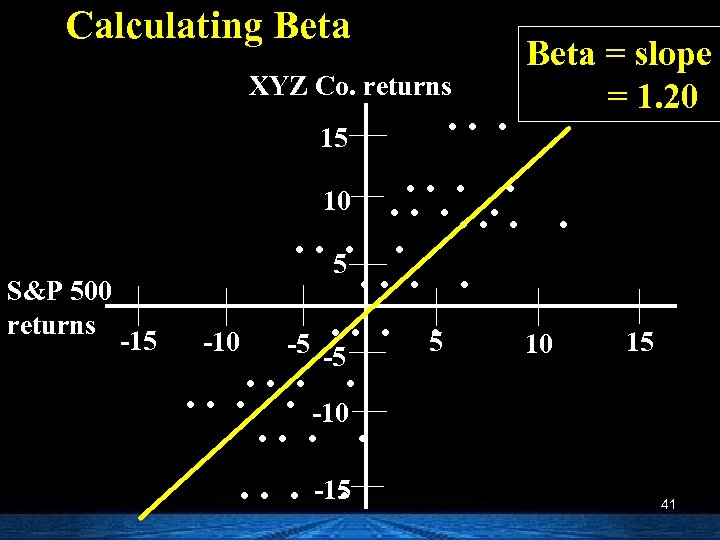
Calculating Beta XYZ Co. returns 15 S&P 500 returns -15 . . . Beta = slope = 1. 20 . . 10. . . 5. -10 -5 -5 10. . . . -10. . . . -15. 15 41

Summary: We know how to measure risk, using standard deviation for overall risk and beta for market risk. n We know how to reduce overall risk to only market risk through diversification. n We need to know how to price risk so we will know how much extra return we should require for accepting extra risk. n 42

What is the Required Rate of Return? n The return on an investment required by an investor given market interest rates and the investment’s risk. 43
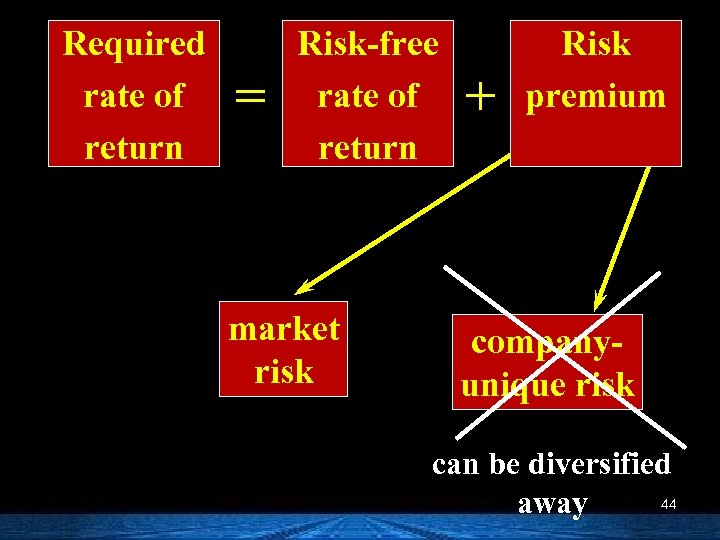
Required rate of return = Risk-free rate of return market risk + Risk premium companyunique risk can be diversified 44 away

This linear relationship between risk and required return is known as the Capital Asset Pricing Model (CAPM). 45

The CAPM equation: rj = rrf + b j (rm - rrf ) where: rj = the required return on security j, rrf = the risk-free rate of interest, b j = the beta of security j, and rm = the return on the market index. 46
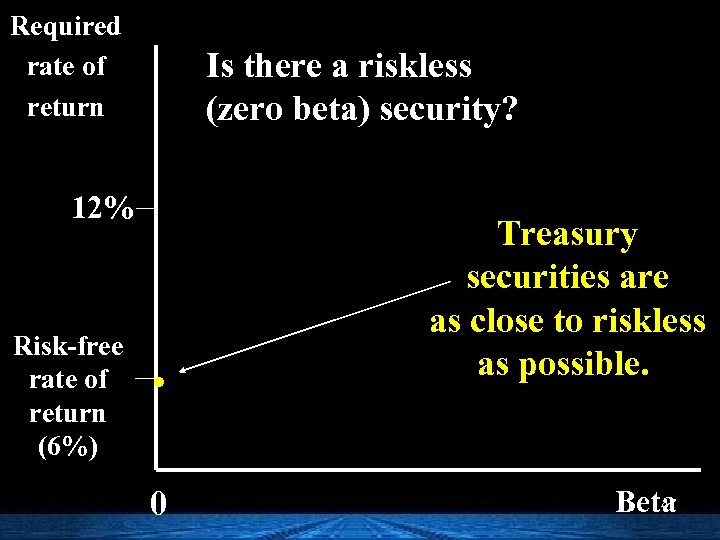
Required rate of return Is there a riskless (zero beta) security? 12% Risk-free rate of return (6%) . 0 Treasury securities are as close to riskless as possible. 47 Beta

Required rate of return How to find the return of the market portfolio? . 12% Risk-free rate of return (6%) . 0 1 Stock market index could be used to approximate the market portfolio. 48 Beta
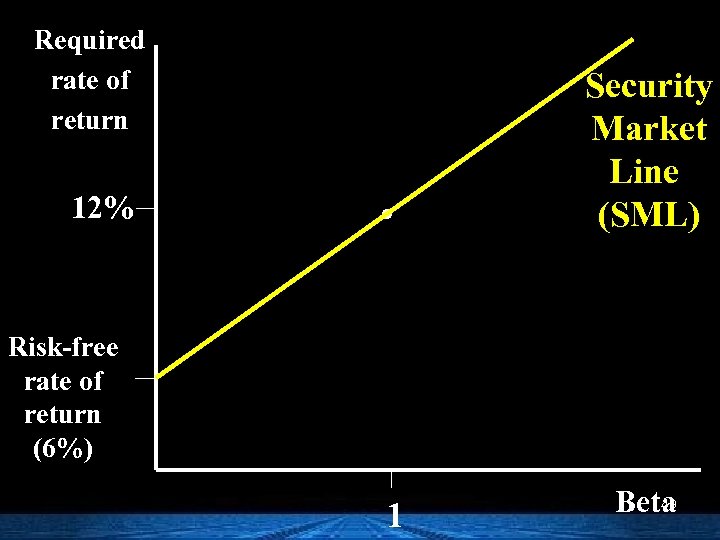
Required rate of return 12% . Security Market Line (SML) Risk-free rate of return (6%) 1 49 Beta

What does beta tell us? A beta of 1 implies the asset has the same systematic risk as the overall market n A beta < 1 implies the asset has less systematic risk than the overall market n A beta > 1 implies the asset has more systematic risk than the overall market n 50
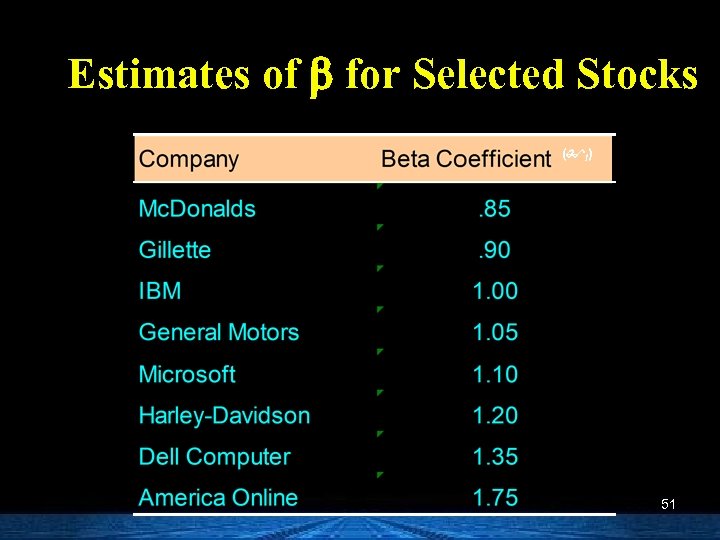
Estimates of b for Selected Stocks ( I) 51
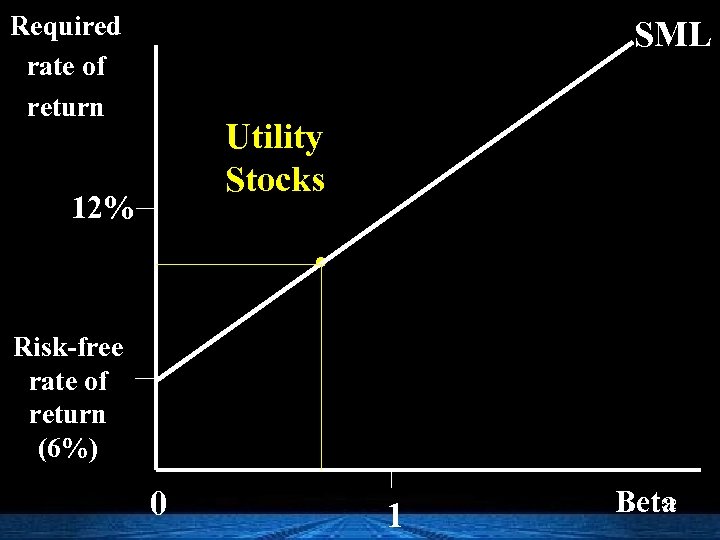
Required rate of return SML Utility Stocks 12% . Risk-free rate of return (6%) 0 1 52 Beta
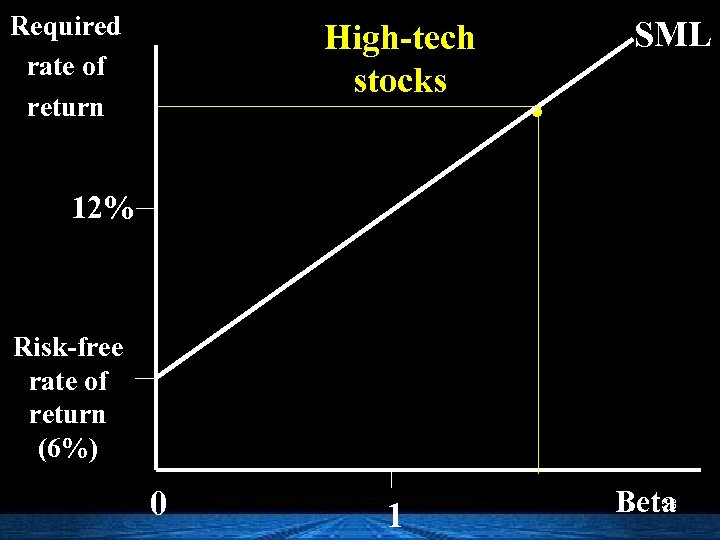
Required rate of return High-tech stocks SML . 12% Risk-free rate of return (6%) 0 1 53 Beta

Example: n Suppose the Treasury bond rate is 6%, the average return on the S&P 500 index is 12%, and Walt Disney has a beta of 1. 2. n According to the CAPM, what should be the required rate of return on Disney stock? 54

rj = rrf + b (rm - rrf ) rj =. 06 + 1. 2 (. 12 -. 06) rj =. 132 = 13. 2% According to the CAPM, Disney stock should be priced to give a 13. 2% return. 55
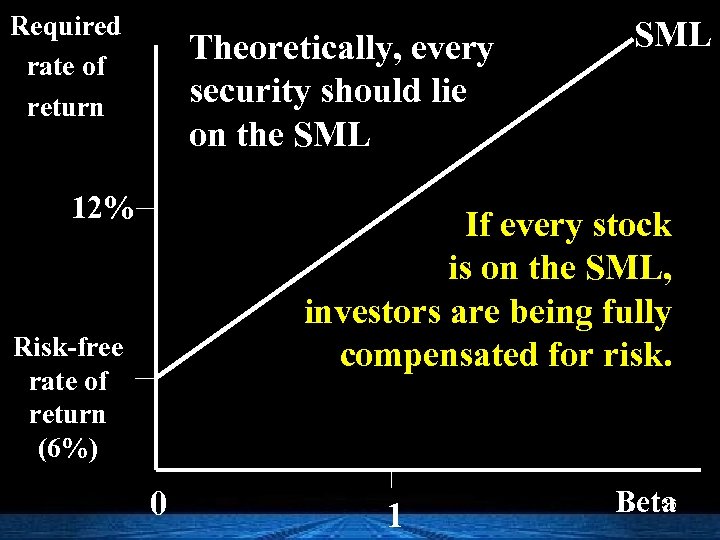
Required rate of return Theoretically, every security should lie on the SML 12% SML If every stock is on the SML, investors are being fully compensated for risk. Risk-free rate of return (6%) 0 1 56 Beta
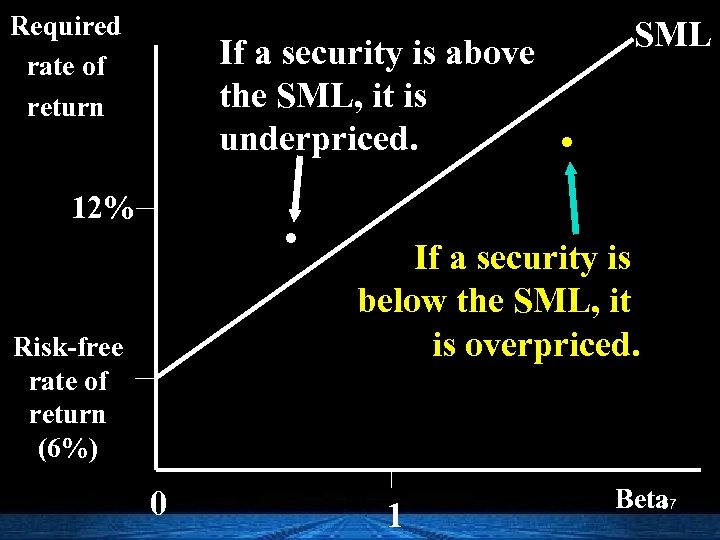
Required rate of return If a security is above the SML, it is underpriced. . 12% Risk-free rate of return (6%) 0 SML . If a security is below the SML, it is overpriced. 1 Beta 57

Total versus Systematic Risk n Consider the following information: Standard Deviation Beta – Security C 20% 1. 25 – Security K 30% 0. 95 n Which security has more total risk? n Which security has more systematic risk? n Which security should have the higher expected return? 58
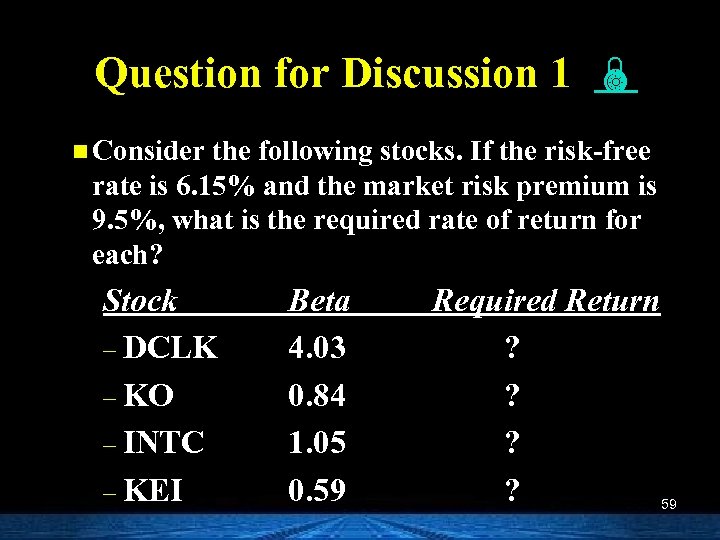
Question for Discussion 1 n Consider the following stocks. If the risk-free rate is 6. 15% and the market risk premium is 9. 5%, what is the required rate of return for each? Stock – DCLK – KO – INTC – KEI Beta 4. 03 0. 84 1. 05 0. 59 Required Return ? ? 59

Portfolio Beta n Weighted average of the individual stock betas with the weights being equal to the proportion of the portfolio invested in each security n Portfolio beta indicates the percentage change on average of the portfolio for every 1 percent change in the general market 60
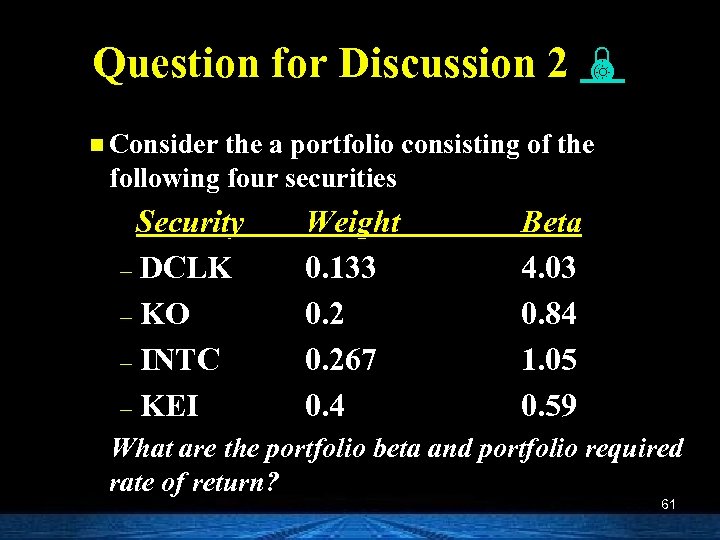
Question for Discussion 2 n Consider the a portfolio consisting of the following four securities Security – DCLK – KO – INTC – KEI Weight 0. 133 0. 267 0. 4 Beta 4. 03 0. 84 1. 05 0. 59 What are the portfolio beta and portfolio required rate of return? 61

Diversification and Beta measures systematic risk n Diversification does not mean to reduce beta n Investors differ in the extent to which they will take risk, so they choose securities with different betas – E. g. , an aggressive investor could choose a portfolio with a beta of 2. 0 – E. g. , a conservative investor could choose a portfolio with a beta of 0. 5 62 n

63

Answer 1 Security Required Rate of Return DCLK – KO – INTC – KEI 6. 15% + 4. 03(9. 5%) = 44. 435% 6. 15% + 0. 84(9. 5%) = 14. 130% 6. 15% + 1. 05(9. 5%) = 16. 125% 6. 15% + 0. 59(9. 5%) = 11. 755% – 64

Answer 2 n Portfolio beta = 0. 133(4. 03)+0. 2(0. 84)+0. 267(1. 05)+0. 4(0. 59) = 1. 22 n Portfolio required rate of return =6. 15%+1. 22(9. 5%) =17. 74% 65
fafb137e3a2a62c3cd4057029e8fa956.ppt