Axiomatic Verification II Software Testing and Verification Lecture

Axiomatic Verification II Software Testing and Verification Lecture Notes 18 Prepared by Stephen M. Thebaut, Ph. D. University of Florida

Axiomatic Verification II • Reasoning about iteration (while loops) • Strong correctness and proving termination

Review of Proof Rules • Before proceeding to while loops, let’s capture our previous reasoning about sequencing, selection statements, and state condition replacement in appropriate rules of inference (ROI). ROI for Sequencing: {P} S 1 {R}, {R} S 2 {Q} {P} S 1; S 2 {Q}

Review of Proof Rules (cont’d) ROI for if_then_else statement: {P Л b } S 1 {Q}, {P Л b} S 2 {Q} {P} if b then S 1 else S 2 {Q} ROI for if_then statement: {P Л b } S {Q}, (P Л b) Q {P} if b then S {Q}

Review of Proof Rules (cont’d) ROI for State Condition Replacement†: K P, {P} S {Q}, Q W {K} S {W} † Also known as the CONSEQUENCE rule.

Reasoning about Iteration • Consider the assertion: {P} while b do S {Q} • What are the necessary conditions for this assertion to hold?

Necessary Conditions: while_do So, we know that {P} while b do S {Q} will hold if the following conditions hold: Case 0: (P Л b) Q Case 1: {P Л b} S {K 1}, (K 1 Л b) Q … … Case 2: {K 1 Л b} S {K 2}, (K 2 Л b) Q Case N: {KN-1 Л b} S {KN}, (KN Л b) Q Great! But who has the time to show that an infinite number of conditions hold?

Reasoning about Iteration (cont’d) • To eliminate the infinite sequence of conditions, replace each Ki with I (where I Ki for every i). Then the conditions above become: Case 0: (P Л b) Q Case 1: {P Л b} S {I}, (I Л b) Q All other Cases: {I Л b} S {I} • To simplify, require further that P I. Then the four conditions reduce to three: P I, {I Л b} S {I}, (I Л b) Q

Reasoning about Iteration (cont’d) • Thus, a ROI for the while_do statement is: P I, {I Л b} S {I}, (I Л b) Q {P} while b do S {Q} where three antecedents are sometimes given the names initialization, preservation, and finalization, respectively. • The assertion “I” in this context is informally referred to as an Invariant, or more precisely as a Q-adequate loop invariant.

Invariants and Q-adequate invariants • A loop invariant is a Boolean-valued predicate that satisfies initialization and preservation. • A Q-adequate loop invariant is a loop invariant that also satisfies finalization. • Note that there may be an arbitrary number of valid loop invariants. For example, TRUE is a trivial loop invariant for any while loop. • The stronger the invariant, the more one can conclude from it together with b.

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I Preservation: {I Л b} S {I} Finalization: (I Л b) Q

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} P Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I What is “P”? (Z=X Л J=1)

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} P Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I What is “P”? (Z=X Л J=1) Does (Z=X Л J=1) Z=XJ? X=X(1)

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} P Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I What is “P”? (Z=X Л J=1) Does (Z=X Л J=1) Z=XJ? Yep!

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X b J : = 1 while J<>Y do Z : = Z+X S J : = J+1 end_while {Z=XY} Initialization: P I Preservation: {I Л b} S {I} {Z=XJ Л J Y} Z : = Z+X {Z=X(J+1) Л J Y} J : = J+1 {Z=X((J-1)+1) Л J-1 Y} Z=XJ

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I Preservation: {I Л b} S {I}

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I Preservation: {I Л b} S {I} Finalization: (I Л b) Q

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I Preservation: {I Л b} S {I} Finalization: (I Л b) Q Does (Z=XJ Л J=Y) Z=XY? XJ=X(J) Yep!

Example 3 Use the Q-adequate invariant I: Z=XJ to prove: {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY} Initialization: P I Preservation: {I Л b} S {I} Finalization: (I Л b) Q

Heuristics for Identifying “I” 1. Hypothesize a predicate that reflects the incremental progress made toward satisfying Q with each iteration. 2. Check finalization. If necessary, refine the predicate so as to be just strong enough to imply Q on termination (i. e. , when b becomes false). 3. Check initialization. If necessary, refine the predicate so as to be just weak enough to be implied by P and return to step (2). 4. Check preservation. If necessary, refine the predicate so as to ensure preservation with respect to S and return to step (2).

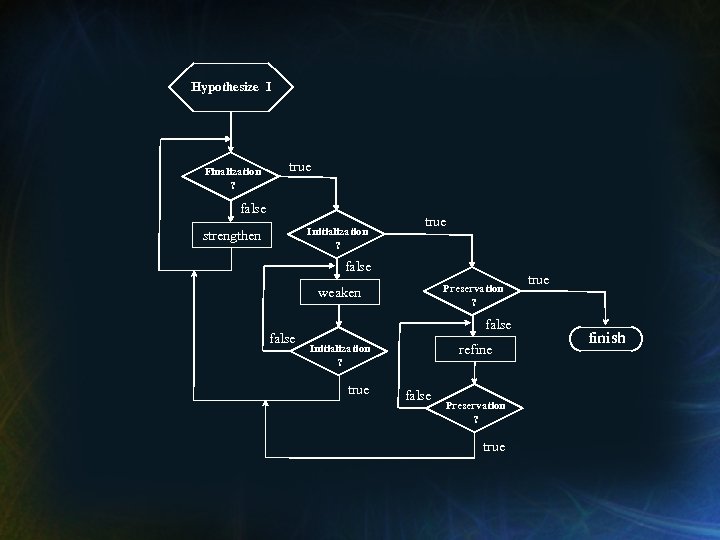Hypothesize I Finalization ? true false Initialization ? strengthen true false Preservation ? weaken false refine Initialization ? true false Preservation ? true finish

Example 4 Synthesize a Q-adequate invariant and prove: Hypothesized I: {N 1} J-1 Sum : = 0 Sum = X[i] i=1 J : = 1 Does finalization while J<=N do hold? I. e. , does Sum : = Sum + X[J] J-1 J : = J+1 (Sum = X[i] Л J>N) end_while i=1 N {Sum = X[i]} i=1 N Sum = X[i]? i=1 Nope!

Example 4 Synthesize a Q-adequate invariant and prove: Hypothesized I: (try #2) {N 1} J-1 Sum : = 0 Sum = X[i] Л J N+1 i=1 J : = 1 Does finalization while J<=N do hold? I. e. , does Sum : = Sum + X[J] J-1 J : = J+1 (Sum = X[i] Л J N+1 Л end_while i=1 N {Sum = X[i]} N J>N) Sum = X[i]? i=1 Yep!

Example 4 Synthesize a Q-adequate invariant and prove: Hypothesized I: (try #2) {N 1} Sum : = 0 J : = 1 while J<=N do Sum : = Sum + X[J] J : = J+1 end_while N {Sum = X[i]} i=1 J-1 Sum = X[i] Л J N+1 i=1 Finalization

Example 4 Synthesize a Q-adequate invariant and prove: {N 1} Hypothesized I: (try #2) J-1 Sum : = 0 Sum = X[i] Л J N+1 i=1 J : = 1 Does initialization while J<=N do hold? I. e. , does Sum : = Sum + X[J] J : = J+1 (N 1 Л Sum=0 Л J=1) end_while J-1 N (Sum = X[i] Л J N+1)? i=1 {Sum = X[i]} i=1 Yep!

Example 4 Synthesize a Q-adequate invariant and prove: Hypothesized I: (try #2) {N 1} Sum : = 0 J : = 1 while J<=N do Sum : = Sum + X[J] J : = J+1 end_while N {Sum = X[i]} i=1 J-1 Sum = X[i] Л J N+1 i=1 Finalization Initialization

Example 4 Synthesize a Q-adequate invariant and prove: Hypothesized I: (try #2) {N 1} J-1 Sum : = 0 Sum = X[i] Л J N+1 i=1 J : = 1 while J<=N do Does preservation hold? J-1 Sum : = Sum + X[J] {Sum = X[i] Л J N+1 Л J N} J : = J+1 i=1 Sum : = Sum + X[J] end_while J N {Sum = X[i] Л J N} {Sum = X[i]} i=1 J : = J+1 J-1 {Sum = X[i] Л J-1 N} = {I} i=1

Example 4 Synthesize a Q-adequate invariant and prove: Hypothesized I: (try #2) {N 1} Sum : = 0 J : = 1 while J<=N do Sum : = Sum + X[J] J : = J+1 end_while N {Sum = X[i]} i=1 J-1 Sum = X[i] Л J N+1 i=1 Finalization Initialization Preservation

Strong Correctness • Program S is said to be strongly correct with respect to pre-condition P and postcondition Q iff: 1. {P} S {Q} (i. e. , S is weakly correct with respect to P and Q), and 2. P implies that S will terminate.

Strong Correctness (cont’d) • Is it possible to prove that a program will terminate? • Are there programs for which termination is undecidable? To write a program which should terminate but doesn’t is a minor sin. To write a program for which termination is undecidable is a major sin. –Harlan Mills

Let’s Pause for a Moment… I remember, as a young boy, watching small, brown frogs jump from Lilly pad to Lilly pad in the pond behind our house. They seemed to never tire of this…

Proving Termination – the Method of Well-Founded Sets† For each program loop, identify a measure based on one or more program variables that satisfies the following properties: 1. decreases (or increases) with each iteration 2. is bounded from below (or above), and 3. can assume only a finite number of values before reaching the bound †A well-founded set (S, >) consists of a set of elements S and an ordering > defined on the elements, such that there can be no infinite descending sequences of elements.

Proving Termination – the Method of Well-Founded Sets (cont’d) • Example: consider a linear search of an unordered list for the value K: {true} Found : = false J : = 1 while (J<=N and (not Found)) do Found : = (K=X[J]) J : = J+1 end_while {(Found Л K=X[J-1]) V ( Found Л i∈{1, …, N} • K X[i])}

Proving Termination – the Method of Well-Founded Sets (cont’d) Proof of termination: Measure: “J” 1. J increases with each iteration since J: =J+1 is executed with each iteration and J does not otherwise change. 2. J is bounded from above (by N+1) since if J exceeds N, J<=N will evaluate to false and the loop must terminate.

Proving Termination – the Method of Well-Founded Sets (cont’d) Proof of termination: (cont’d) 3. Since J increases by an integral amount with each iteration, it can assume only a finite number of values before reaching N+1: {1, 2, …, N, N+1}. Therefore, by the Method of Well-Founded Sets, the loop must terminate.

Exercise • The weak correctness of the assertion below was established earlier. Can the Method of Well-Founded Sets be used to prove the program will terminate? {true} Z : = X J : = 1 while J<>Y do Z : = Z+X J : = J+1 end_while {Z=XY}

A while_do ROI for strong correctness • We can incorporate a termination term, t, in the while loop ROI. • Let t denote a whole number† which decreases with each iteration and implies termination when less than or equal to 0: P I, (IЛb) (t>0), {IЛb. Лt=N} S {IЛt

Problem Set 5: Axiomatic Verification • Note especially. . . – Problem 4: deriving and using a suitable Rule of Inference for the “repeat_until” construct, and – Problem 6: alternative, hypothesized Rules of Inference for the “while” construct. . . are they valid or not?

Axiomatic Verification II Software Testing and Verification Lecture Notes 18 Prepared by Stephen M. Thebaut, Ph. D. University of Florida