Автор Попель Петр Станиславович Презентация Симонова Оксана Александровна

Автор: Попель Петр Станиславович Презентация: Симонова Оксана Александровна Попель П. С. Электромагнетизм.

1. Поляризация диэлектриков в электрическом поле. 2. Вектор поляризации (поляризованность) и его зависимость от напряженности электрического поля. 3. Возникновение связанных зарядов на поверхности и в объеме диэлектрика, находящегося во внешнем электрическом поле. 4. Теорема Гаусса для вектора поляризации. 5. Связь поверхностной плотности связанных зарядов с вектором поляризации. Попель П. С. Электромагнетизм.

Молекулы веществ делятся на полярные и неполярные. В молекулах в отсутствие внешнего электрического поля центры положительного и отрицательного зарядов совпадают; молекула электронейтральна и не имеет дипольного момента. молекулы и в отсутствие внешнего электрического поля являются диполями, поскольку центры положительного и отрицательного зарядов у них смещены. + Попель П. С. Электромагнетизм.

а) неполярные молекулы не имеют дипольного момента, значит, и их суммарный дипольный момент б) полярные молекулы ориентированы хаотически, значит, векторная сумма их дипольных моментов равна нулю: В тех случаях, когда диэлектрик не поляризован. Попель П. С. Электромагнетизм. говорят, что

а) в неполярных молекулах происходит смещение центров положительных и отрицательных зарядов в противоположных направлениях; + молекулы приобретают дипольные моменты , ориентированные параллельно другу. Теперь уже и говорят, что диэлектрик поляризован. Этот вид поляризации называется Попель П. С. Электромагнетизм.

б) полярные молекулы стремятся сориентироваться своими дипольными моментами по направлению внешнего поля; этому препятствует тепловое движение молекул. В результате устанавливается некоторая предпочтительная ориентация полярных молекул: + Теперь диэлектрик поляризован. Этот вид поляризации называется Попель П. С. Электромагнетизм.

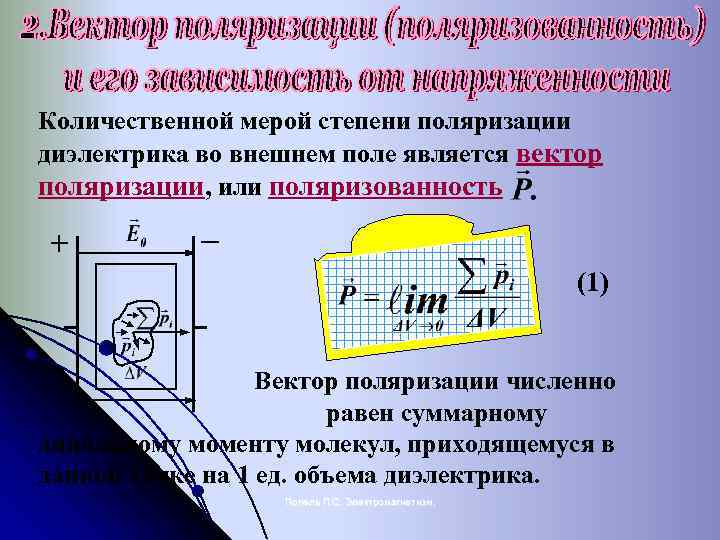Количественной мерой степени поляризации диэлектрика во внешнем поле является вектор поляризации, или поляризованность + (1) Вектор поляризации численно равен суммарному дипольному моменту молекул, приходящемуся в данной точке на 1 ед. объема диэлектрика. Попель П. С. Электромагнетизм.

Умножим и разделим (1) на △N – число молекул диэлектрика в объеме △V: + - концентрация частиц в данной точке диэлектрика. - средний дипольный момент молекулы. (2) Попель П. С. Электромагнетизм.

Для большинства диэлектриков, находящихся в не слишком сильном электрическом поле, где æ (3) - напряженность электрического поля внутри диэлектрика; æ - диэлектрическая восприимчивость диэлектрика. - некоторые ионные кристаллы; - электреты; - сегнетоэлектрики. Попель П. С. Электромагнетизм.

Х Х а) пластина из нейтрального (незаряженного) неоднородного диэлектрика, плотность которого возрастает в направлении оси ОХ. б) распределение объемной плотности положительного (ρ′+) и отрицательного (ρ′-) зарядов в отсутствие внешнего поля; в любой точке ρ′+=|ρ′-| и суммарный заряд равен нулю. Попель П. С. Электромагнетизм.

в) при включении внешнего поля положительные заряды смещаются по полю, отрицательные - против поля. Х В итоге и на поверхностях диэлектрика, и в его объеме появляются нескомпенсированные заряды. Если бы диэлектрик был однородным (ρ′+ =const; ρ′- =const), тогда при включении + + электрического поля + + + нескомпенсированные заряды + + + появились бы только на + Х Х поверхностях диэлектрика. + + + + Попель П. С. Электромагнетизм.

+ + + ∆V – малый объем внутри диэлектрика. Положительный заряд внутри объема ∆V равен ρ′+ · ∆V. При включении внешнего поля этот заряд сместится относительно отрицательного заряда в среднем на вектор. Тогда объем ∆V приобретет суммарный дипольный момент Разделим на ∆V: (4) ( ℓ не превышает размеров атома или молекулы диэлектрика!). Попель П. С. Электромагнетизм.

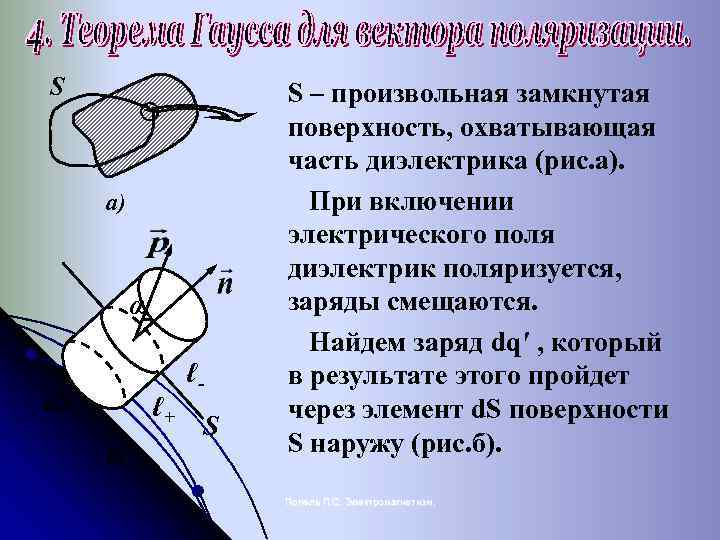S а) α d. S ℓ+ б) ℓS S – произвольная замкнутая поверхность, охватывающая часть диэлектрика (рис. а). При включении электрического поля диэлектрик поляризуется, заряды смещаются. Найдем заряд dq′ , который в результате этого пройдет через элемент d. S поверхности S наружу (рис. б). Попель П. С. Электромагнетизм.

- векторы смещения “+” и “- ” зарядов при поляризации. α Через d. S наружу выйдет положительный заряд, заключенный во ℓ- “внутренней” части косого цилиндра; d. S ℓ+ S он равен Одновременно внутрь войдет отрицательный заряд, равный (ρ-<0). Это равносильно переходу наружу положительного заряда, равного Суммарный связанный заряд, выходящий через d. S наружу: (5) Попель П. С. Электромагнетизм.

(5) Поскольку , то (6) α d. S ℓ- ℓ+ S где - расстояние, на которое сместились при поляризации друг относительно друга “+” и “-” связанные заряды диэлектрика. Поскольку (см. (4)), то (7) Попель П. С. Электромагнетизм.

При переходе через d. S наружу положительного заряда dq′ в объеме, ограниченном поверхностью S, появится заряд, равный – dq′. Общий заряд, возникший внутри поверхности S вследствие поляризации, равен S ↝ Теорема Гаусса для вектора. (8) Поток вектора поляризации через произвольную замкнутую поверхность S равен по величине суммарному связанному заряду, возникшему внутри поверхности S вследствие поляризации, и противоположен ему по знаку. Попель П. С. Электромагнетизм.

Поскольку в (8) где V – объем диэлектрика, лежащий внутри поверхности S, ρ′ - объемная плотность связанных зарядов, то Для бесконечно малого объема Значит, Выражение стоящее слева – это дивергенция вектора т. е. Дифференциальная , (9) форма теоремы Гаусса для вектора. Попель П. С. Электромагнетизм.

Рассмотрим случай однородного и изотропного диэлектрика. Для него, согласно (3), и (8) принимает вид: (10) Но по теореме Гаусса для вектора ⇜ ⇜ Сторонний заряд Попель П. С. Электромагнетизм. , (11) Связанный заряд

Объединяя (10) и (11), получаем: , т. е. (12) В однородном изотропном диэлектрике, в котором отсутствуют сторонние заряды (q=0), связанный объемный заряд возникнуть не может; связанные заряды в этом случае появляются только на поверхностях диэлектрика. Попель П. С. Электромагнетизм.

2 1 - поверхностная плотность связанного заряда. Выделена бесконечно малая гауссова замкнутая поверхность. Согласно теореме (8), (13) где - проекции вектора в диэлектрике 1 на нормаль и в диэлектрике 2 – на нормаль. Очевидно, , где - проекция на нормаль , тогда (14) Попель П. С. Электромагнетизм.

(14) 2 1 на границе раздела диэлектриков нормальная составляющая вектора испытывает разрыв, величине которого зависит от. на границе диэлектрика с вакуумом Р 2 n =0 и из ( 14 ) следует: , (15) где pn – проекция вектора на внешнюю нормаль к поверхности диэлектрика в данной точке. Попель П. С. Электромагнетизм.