Автоматика и регулирование АД и ЭУ Основные

Автоматика и регулирование АД и ЭУ

Основные понятия Автоматика – раздел науки и техники, изучающий теорию и принципы построения систем управления, действующих без непосредственного участия человека. Управление – целенаправленное воздействие на процессы Управляющий процесс Управляемый процесс

Основные понятия В технических системах: Процесс – некоторое взаимодействие элементов и компонентов установки, машины, агрегата, характеризующееся определенными соотношениями параметров. Управление – преднамеренное воздействие на технические процессы с целью получения нужных параметров от какого-либо устройства или их совокупности. Автоматическое Полуавтоматическое Ручное

Основные понятия В технических системах: Регулирование – частный случай управления – преднамеренное воздействие на устройство, когда контролируемый им параметр отклоняется от требуемого, обычно стабилизированного значения. Автоматическое Полуавтоматическое Ручное

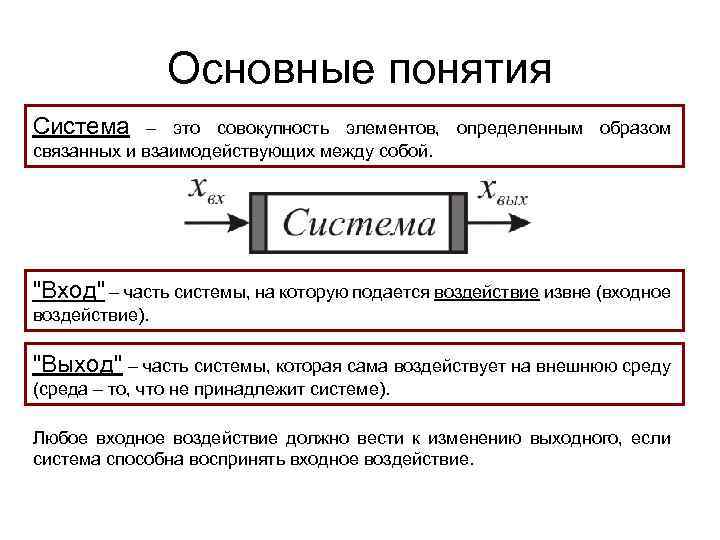Основные понятия Система – это совокупность элементов, определенным образом связанных и взаимодействующих между собой. "Вход" – часть системы, на которую подается воздействие извне (входное воздействие). "Выход" – часть системы, которая сама воздействует на внешнюю среду (среда – то, что не принадлежит системе). Любое входное воздействие должно вести к изменению выходного, если система способна воспринять входное воздействие.

Основные понятия Путь – совокупность частей системы, по которым происходит передача воздействий от внешней среды к системе или между ее отдельными частями. Сигнал – обусловленное (заранее оговоренное) состояние или изменение состояния количественного показателя (параметра) физической величины, посредством которого передается воздействие. Сигнал выражается какой-либо математической функцией (изменение информации о воздействии во времени). Воздействия в АД: сила тока, напряжение, угол поворота вала двигателя хвх, хвых – сигналы входного и выходного воздействия Закон (алгоритм) управления – взаимосвязь входного и выходного воздействия. Представляют в виде: словесного описания, графика, схемы, таблицы, дифференциального или алгебраического уравнения. Входящие в уравнения коэффициенты и константы определяют свойства системы.

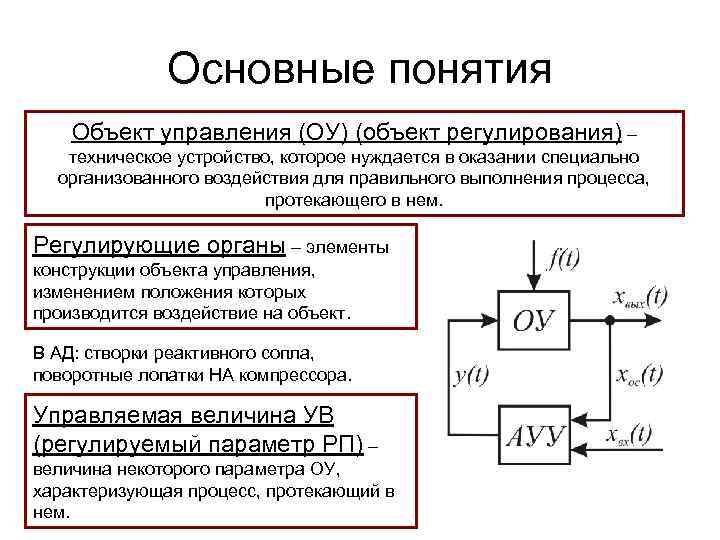Основные понятия Объект управления (ОУ) (объект регулирования) – техническое устройство, которое нуждается в оказании специально организованного воздействия для правильного выполнения процесса, протекающего в нем. Регулирующие органы – элементы конструкции объекта управления, изменением положения которых производится воздействие на объект. В АД: створки реактивного сопла, поворотные лопатки НА компрессора. Управляемая величина УВ (регулируемый параметр РП) – величина некоторого параметра ОУ, характеризующая процесс, протекающий в нем.

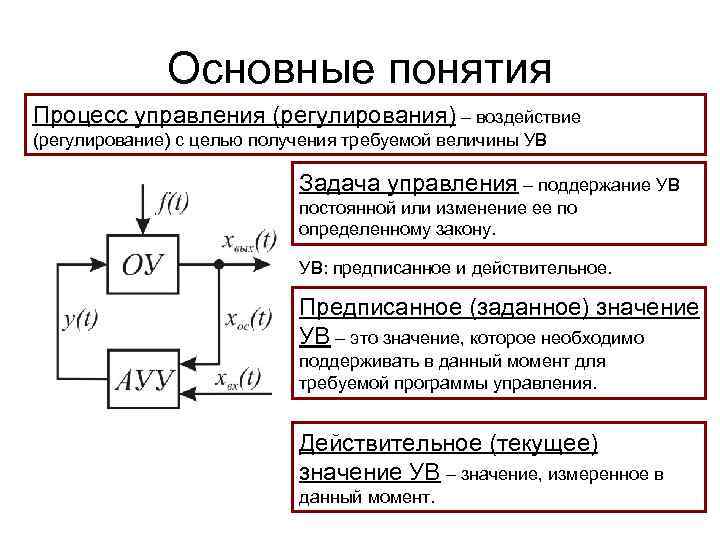Основные понятия Процесс управления (регулирования) – воздействие (регулирование) с целью получения требуемой величины УВ Задача управления – поддержание УВ постоянной или изменение ее по определенному закону. УВ: предписанное и действительное. Предписанное (заданное) значение УВ – это значение, которое необходимо поддерживать в данный момент для требуемой программы управления. Действительное (текущее) значение УВ – значение, измеренное в данный момент.

Основные понятия Автоматическое управляющее устройство (регулятор) – совокупность элементов, приборов и устройств, которые, сравнивая действительное значение управляемой величины с предписанным, автоматически поддерживают их равенство. АУУ сравнивая предписанное и действительное значение УВ, вырабатывает управляющее воздействие (регулирующий фактор РФ) y(t). САУ (САР, если система выполняет только функции регулирования) – совокупность взаимодействующих между собой ОУ и АУУ

Основные понятия Для АД (с неизменяемой геометрией проточной части) УВозд: расход топлива. Для АД (с изменяемой проточной частью) УВозд: расход топлива, площадь критического сечения сопла, площадь проходных сечений поворотных НА, расход топлива в ФК. Число УВозд = число УВ Если число УВозд < число УВ, то необходимо вводить ограничения. При этом УВ становится неуправляемой и ограниченной. Для этого необходимо поставить специальные АУУ – ограничители. В ГТД это могут быть: ограничители максимального числа оборотов ротора и максимального расхода топлива, степени повышения давления воздуха в ОК и максимальной температуры газа за турбиной.

Режимы САУ Установившийся – характеризуется постоянным или колеблющимся с постоянной амплитудой предписанным значением УВ. Неустановившийся – характеризуется изменением во времени предписанного значения УВ, вызванного внешним или внутренним воздействием на систему. Внешним воздействием для ГТД может быть изменение окружающих условий в зависимости от высоты и скорости полета. Внутренним воздействием для ГТД – контрольное воздействие, поступающие по цепи обратной связи или перенастройка одного из элементов управления. После прекращения действия воздействий САУ должна вернуть УВ к исходному или новому значению.

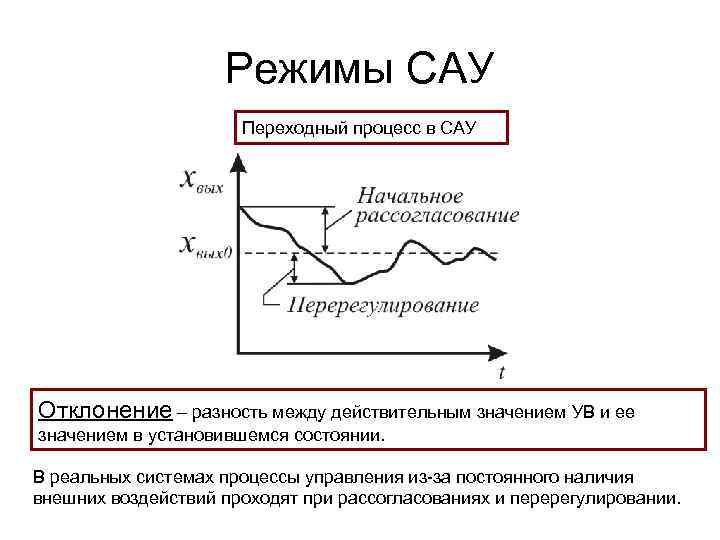Режимы САУ Переходный процесс в САУ Отклонение – разность между действительным значением УВ и ее значением в установившемся состоянии. В реальных системах процессы управления из-за постоянного наличия внешних воздействий проходят при рассогласованиях и перерегулировании.

Классификация САУ По назначению (в зависимости от объекта, над которым осуществляется процесс управления) САУ делятся на: o o самолета ТРД радиолокационной станции металлорежущего станка По характеру УВ САУ делятся на: - скорости вращения роторов температуры давления газа и жидкости напряжения частоты тока и т. д.

Классификация САУ По принципу действия (по характеру алгоритма управления): - разомкнутые (управление по возмущению, принцип компенсации) замкнутые (управление по отклонению) комбинированные принцип адаптации (приспособление) По наличию и виду вспомогательной энергии: - прямого действия непрямого действия: а) электрические б) гидравлические в) пневматические г) комбинированные

Классификация САУ По виду задающей программы (характеру изменения задающего воздействия): - стабилизации слежения оптимальные программные По продолжительности и виду управляющего воздействия: - непрерывные: а) импульсные б) релейные По числу контуров: - одноконтурные многоконтурные

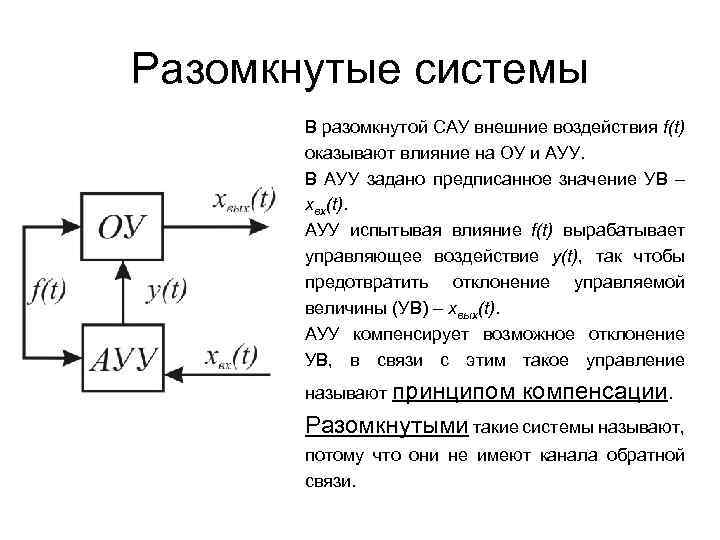Разомкнутые системы В разомкнутой САУ внешние воздействия f(t) оказывают влияние на ОУ и АУУ. В АУУ задано предписанное значение УВ – xвх(t). АУУ испытывая влияние f(t) вырабатывает управляющее воздействие y(t), так чтобы предотвратить отклонение управляемой величины (УВ) – xвых(t). АУУ компенсирует возможное отклонение УВ, в связи с этим такое управление называют принципом компенсации. Разомкнутыми такие системы называют, потому что они не имеют канала обратной связи.

Разомкнутые системы Достоинства РС: 1. 2. 3. простота надежность относительно высокое быстродействие Недостатки РС: 1. невысокая статическая точность поддержания значения УВ из-за отсутствия обратной связи 2. не реагирует на внутридвигательные изменения

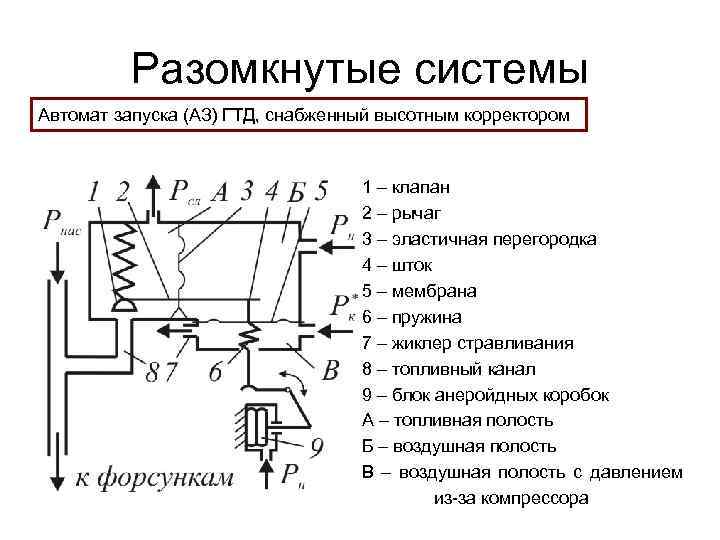Разомкнутые системы Автомат запуска (АЗ) ГТД, снабженный высотным корректором 1 – клапан 2 – рычаг 3 – эластичная перегородка 4 – шток 5 – мембрана 6 – пружина 7 – жиклер стравливания 8 – топливный канал 9 – блок анеройдных коробок А – топливная полость Б – воздушная полость В – воздушная полость с давлением из-за компрессора

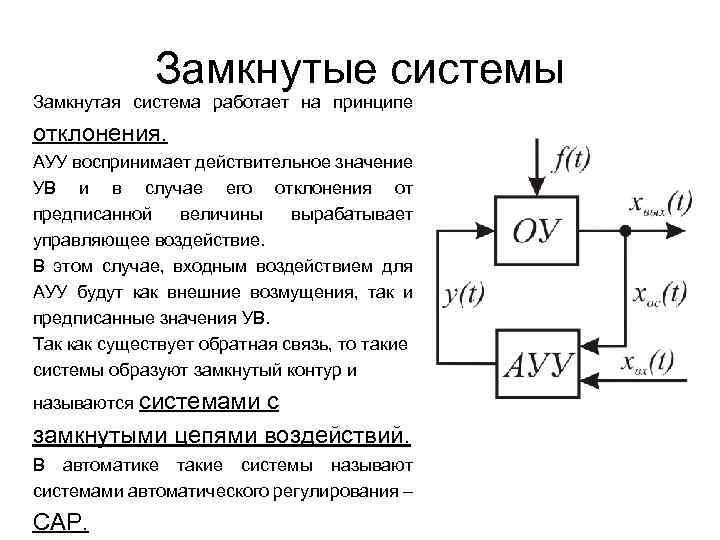Замкнутые системы Замкнутая система работает на принципе отклонения. АУУ воспринимает действительное значение УВ и в случае его отклонения от предписанной величины вырабатывает управляющее воздействие. В этом случае, входным воздействием для АУУ будут как внешние возмущения, так и предписанные значения УВ. Так как существует обратная связь, то такие системы образуют замкнутый контур и называются системами с замкнутыми цепями воздействий. В автоматике такие системы называют системами автоматического регулирования – САР.

Замкнутые системы Достоинства: 1. высокая статическая точность поддержания УВ. Недостатки: 1. относительно малое быстродействие 2. принципиальная невозможность предотвращения отклонения УВ от предписанного значения, поскольку система работает только при наличии отклонения от предписанного.

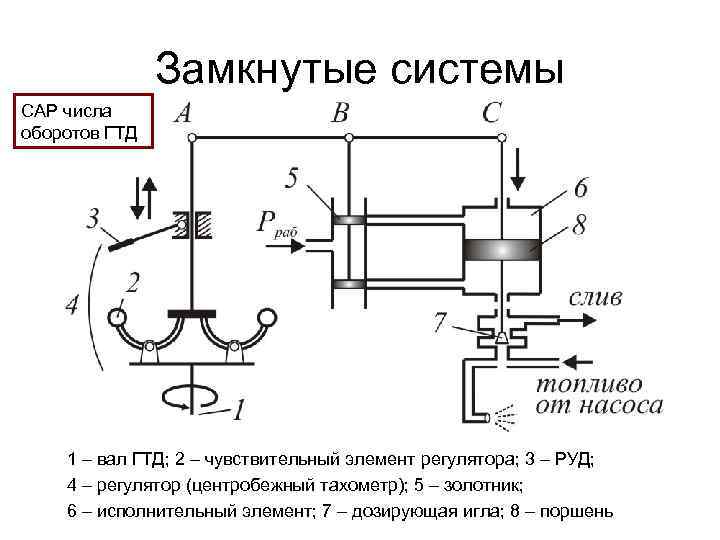Замкнутые системы САР числа оборотов ГТД 1 – вал ГТД; 2 – чувствительный элемент регулятора; 3 – РУД; 4 – регулятор (центробежный тахометр); 5 – золотник; 6 – исполнительный элемент; 7 – дозирующая игла; 8 – поршень

Характеристики САУ Для сравнения САУ между собой необходимо найти универсальные формы выражения свойств Основным признаком определяющим свойства отдельных элементов и систем в целом является связь между хвх и хвых В общем виде такая связь описывается дифференциальным уравнением Решив уравнение можно определить значение УВ в любой момент времени При этом необходимо учитывать вид входного воздействия (возмущающего сигнала) и начальное состояние системы Взаимосвязи между возмущающим воздействием и управляемой величиной называют характеристиками

Статические характеристики Статической характеристикой называют связь между значениями управляемой величины и входного воздействия в установившемся режиме Хвых = f ( Хвх ) Статические характеристики выражают: А) аналитически Б) графически В) таблично Аналитически характеристики получают из уравнения движения системы Для этого общее уравнение движения n-го порядка при подстановке производных = 0 превращают в уравнение статики:

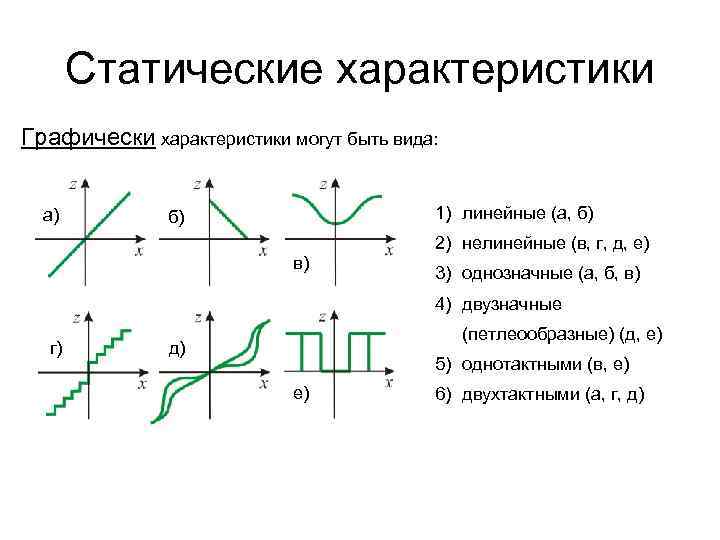Статические характеристики Графически характеристики могут быть вида: а) 1) линейные (а, б) б) в) 2) нелинейные (в, г, д, е) 3) однозначные (а, б, в) 4) двузначные г) (петлеообразные) (д, е) д) 5) однотактными (в, е) е) 6) двухтактными (а, г, д)

Динамические характеристики Динамическая характеристика показывает зависимость управляемой величины от сигналов входных воздействий и их производных в переходном процессе (неустановившемся режиме) Динамические характеристики: А) аналитические: - дифференциальное уравнение - передаточная функция Б) графические В) частотные Обязательными условиями для получения динамических характеристик являются: А) начальные состояние системы (нулевое начальное условие) Б) скачкообразное изменение входного воздействия (часто принимают равным 1)

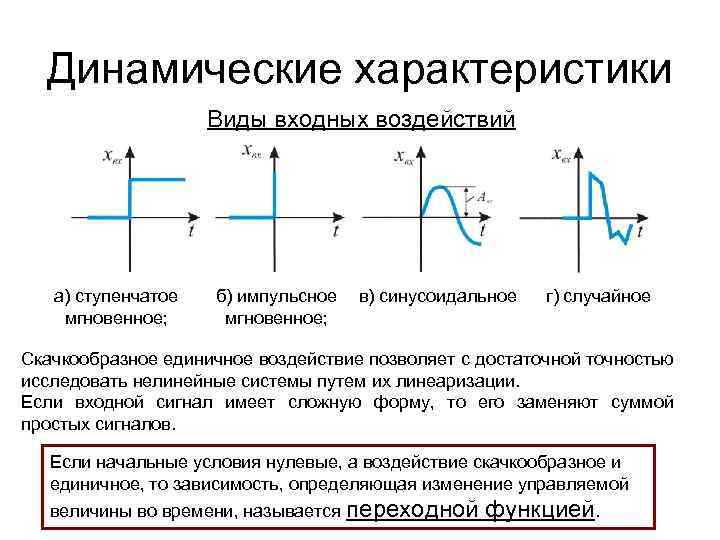Динамические характеристики Виды входных воздействий а) ступенчатое мгновенное; б) импульсное мгновенное; в) синусоидальное г) случайное Скачкообразное единичное воздействие позволяет с достаточной точностью исследовать нелинейные системы путем их линеаризации. Если входной сигнал имеет сложную форму, то его заменяют суммой простых сигналов. Если начальные условия нулевые, а воздействие скачкообразное и единичное, то зависимость, определяющая изменение управляемой величины во времени, называется переходной функцией.

Передаточные функции Для облегчения исследования систем в теорию автоматического регулирования введено понятие передаточной функции. Это отношение по Лапласу выходной Хвых(р) величины к входной Хвх(р) при нулевых начальных условиях (1) Вывод передаточной функции для системы 1 -го порядка: - уравнение движения системы 1 -го порядка Пусть для всех оригиналов функций найдены изображения:

Передаточные функции Запишем уравнение (1) в операторной форме: Необходимо помнить, что передаточная функция получена при нулевых начальных условиях

Передаточные функции Передаточная функция не зависит от вида входного или возмущающего воздействия, а от параметров функциональных элементов, составляющих САУ Введение понятия передаточная функция позволило находить выходную величину не прибегая к сложным расчетам

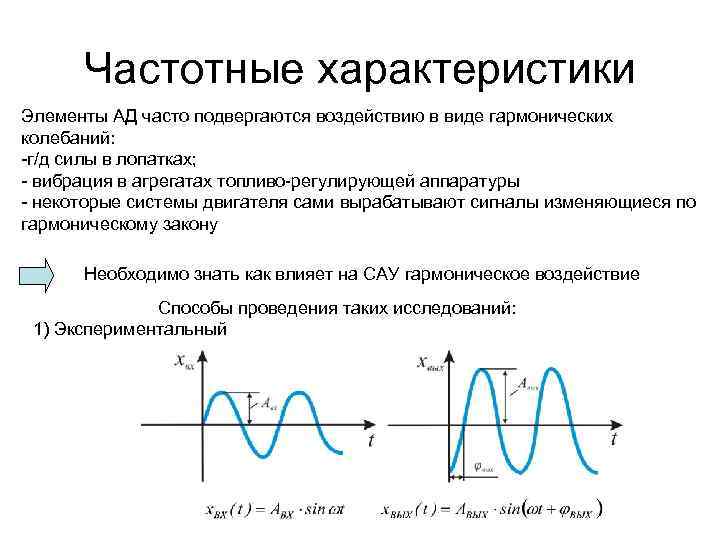Частотные характеристики Элементы АД часто подвергаются воздействию в виде гармонических колебаний: -г/д силы в лопатках; - вибрация в агрегатах топливо-регулирующей аппаратуры - некоторые системы двигателя сами вырабатывают сигналы изменяющиеся по гармоническому закону Необходимо знать как влияет на САУ гармоническое воздействие Способы проведения таких исследований: 1) Экспериментальный

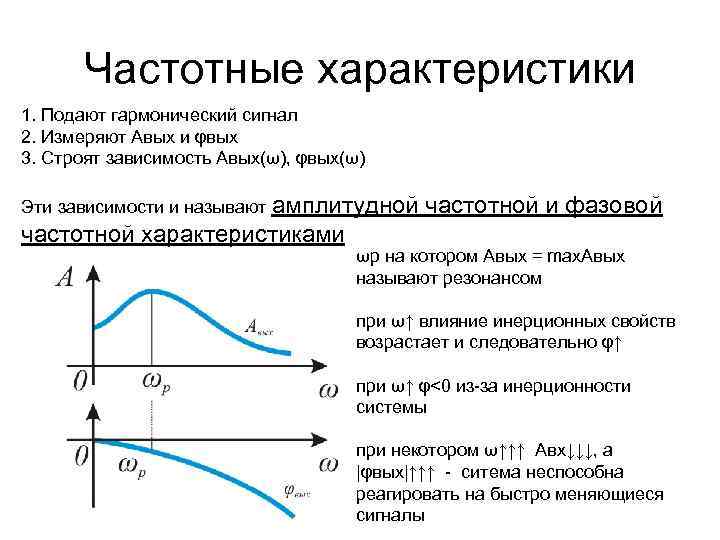Частотные характеристики 1. Подают гармонический сигнал 2. Измеряют Авых и φвых 3. Строят зависимость Авых(ω), φвых(ω) Эти зависимости и называют амплитудной частотной характеристиками частотной и фазовой ωр на котором Авых = max. Авых называют резонансом при ω↑ влияние инерционных свойств возрастает и следовательно φ↑ при ω↑ φ<0 из-за инерционности системы при некотором ω↑↑↑ Авх↓↓↓, а |φвых|↑↑↑ - ситема неспособна реагировать на быстро меняющиеся сигналы

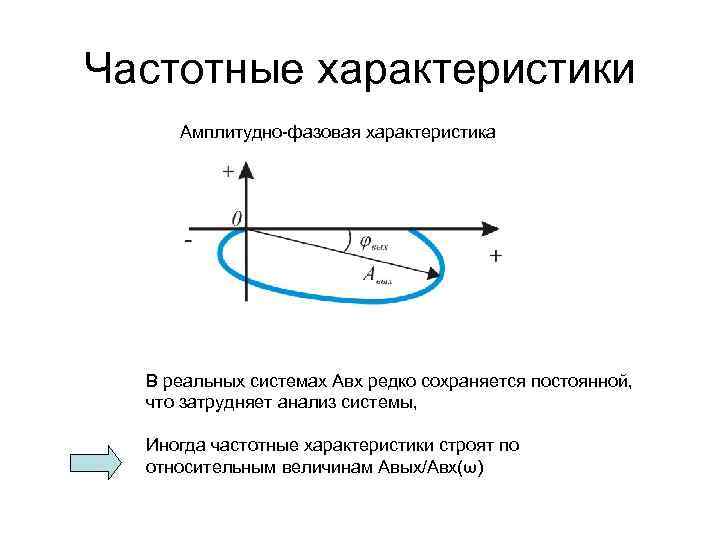Частотные характеристики Амплитудно-фазовая характеристика В реальных системах Авх редко сохраняется постоянной, что затрудняет анализ системы, Иногда частотные характеристики строят по относительным величинам Авых/Авх(ω)

Частотные характеристики 2) Расчетный (если известна передаточная функция) Обычно для этого используют символический метод, основанный на изображении синусоидально меняющихся функций времени показательными функциями с мнимым аргументом Из теории комплексных чисел: Пусть на систему действует входной sin сигнал при Авх=1 Переведем Хвх и Хвых из тригонометрической формы в показательную:

Частотные характеристики Из теории операционного исчисления: Для системы 1 -го порядка: Переведем в изображения:

Частотные характеристики Передаточная функция: где Ее обозначают и называют комплексным коэффициентом передачи или комплексной частотной функцией Для системы 1 -го порядка: По частотным характеристикам одновременно оценивают и статические и динамические свойства систем.

Динамические звенья САУ Анализ систем значительно упрощается, если разделить ее на элементарные звенья САУ можно разделить на звенья по функциональным признакам, однако это не отражает динамические свойства элементов В 1938 г. А. В. Михайлов предложил разделить САУ на звенья по виду их уравнений Элементарным динамическим звеном называют искусственно выделенный элемент автоматической системы, динамические свойства которого описываются дифференциальным уравнением не выше второго порядка. При этом тип звена не зависит от его конструктивного оформления и физической природы процессов, протекающих в нем. Два звена можно считать однотипными, если их дифференциальные уравнения однотипны

Динамические звенья САУ В САУ распространение получили следующие типы звеньев: 1. 2. 3. 4. 5. Пропорциональное Апериодическое Колебательное Интегрирующее Дифференцирующее Динамические свойства каждого звена имеют свои особенности. Переходные процессы в них зависят не только от соотношения выходного и входного сигнала, но и от внутренних свойств самого звена Напомним, что в первоначальный момент времени звенья находились в состоянии покоя, а входные воздействия были мгновенными скачкообразными

Динамические звенья САУ Пропорциональное звено (Усилительное) – звено в котором сигнал на выходе прямо пропорционален сигналу на входе, т. е. свойства звена описываются уравнением нулевого порядка: - коэффициент усиления (ослабления) системы В реальных звеньях всегда есть инерционность. Пропорциональным называется звено инерционностью которого можно пренебречь Примеры: рычаги, дроссельные краны топливных систем, зубчатая передача

Динамические звенья САУ Интегрирующее звено – звено, у которого скорость изменения сигнала выходного воздействия прямо пропорциональна входному сигналу: - коэффициент усиления (передачи) по скорости (при хвх = 1 он равен скорости изменения выходного сигнала) При хвх = 1 (единичное скачкообразное воздействие), то:

Динамические звенья САУ Интегрирующее звено т. е. при постоянном воздействии на звено входным сигналом хвх(t), величина выходного сигнала хвых(t) будет неограниченно возрастать Получим передаточную функцию из уравнения:

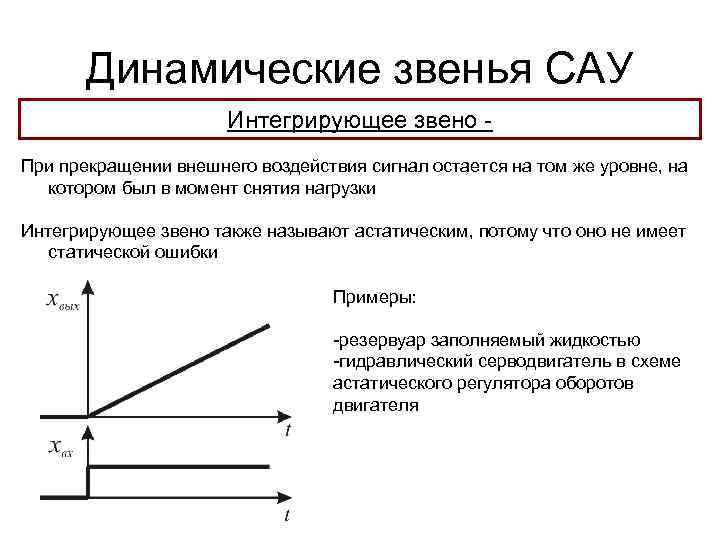Динамические звенья САУ Интегрирующее звено При прекращении внешнего воздействия сигнал остается на том же уровне, на котором был в момент снятия нагрузки Интегрирующее звено также называют астатическим, потому что оно не имеет статической ошибки Примеры: -резервуар заполняемый жидкостью -гидравлический серводвигатель в схеме астатического регулятора оборотов двигателя

Динамические звенья САУ Апериодическое звено – звено в котором при мгновенном воздействии на входе величина входного сигнала стремится к новому установившемуся значению по экспоненте (для устойчивого звена) Переходный процесс носит апериодический характер Та определяет инерционные свойства звена => Инерционное звено

Динамические звенья САУ Апериодическое звено Пропорциональное и интегрирующее звенья – частные случаи апериодического При Та ≈ 0, => пропорциональное звено При Та >>1 => интегрирующее звено Примеры: -термопара -биметаллическая пластина

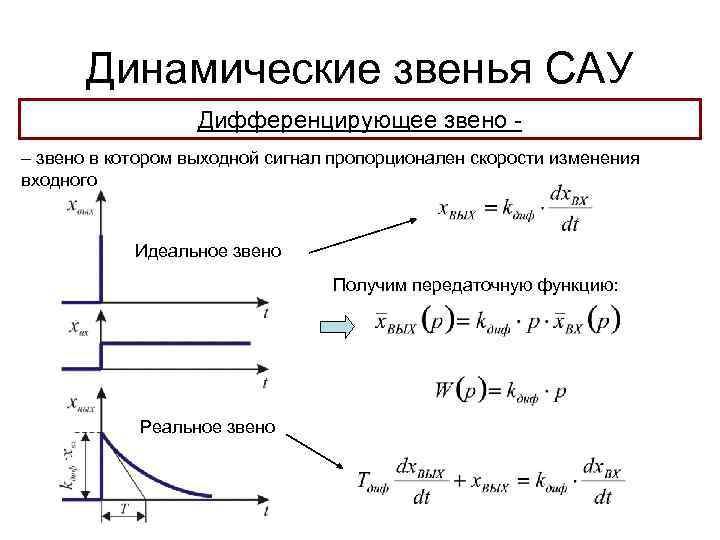Динамические звенья САУ Дифференцирующее звено – звено в котором выходной сигнал пропорционален скорости изменения входного Идеальное звено Получим передаточную функцию: Реальное звено

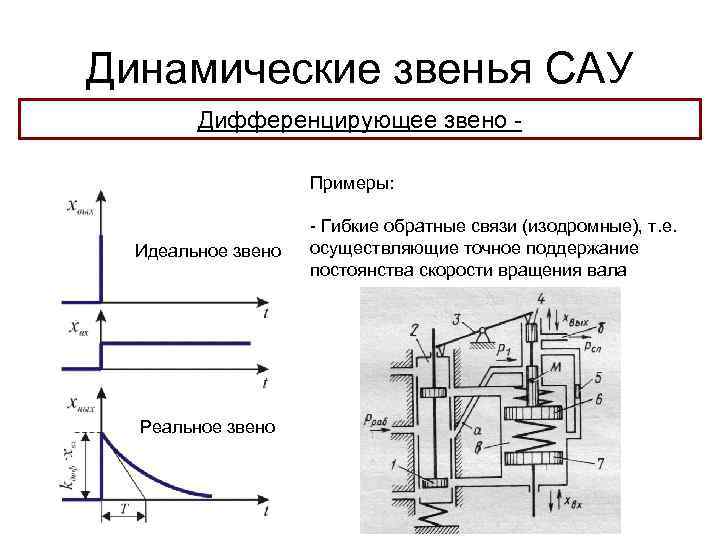Динамические звенья САУ Дифференцирующее звено Примеры: Идеальное звено Реальное звено - Гибкие обратные связи (изодромные), т. е. осуществляющие точное поддержание постоянства скорости вращения вала

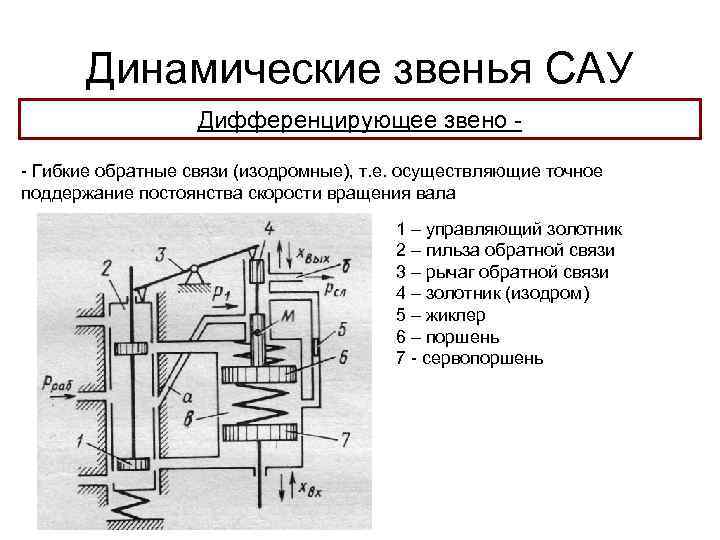Динамические звенья САУ Дифференцирующее звено - Гибкие обратные связи (изодромные), т. е. осуществляющие точное поддержание постоянства скорости вращения вала 1 – управляющий золотник 2 – гильза обратной связи 3 – рычаг обратной связи 4 – золотник (изодром) 5 – жиклер 6 – поршень 7 - сервопоршень

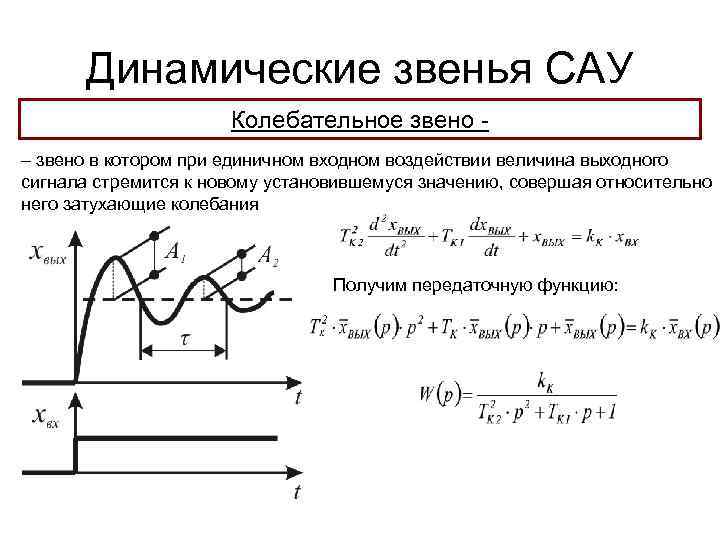Динамические звенья САУ Колебательное звено – звено в котором при единичном входном воздействии величина выходного сигнала стремится к новому установившемуся значению, совершая относительно него затухающие колебания Получим передаточную функцию:

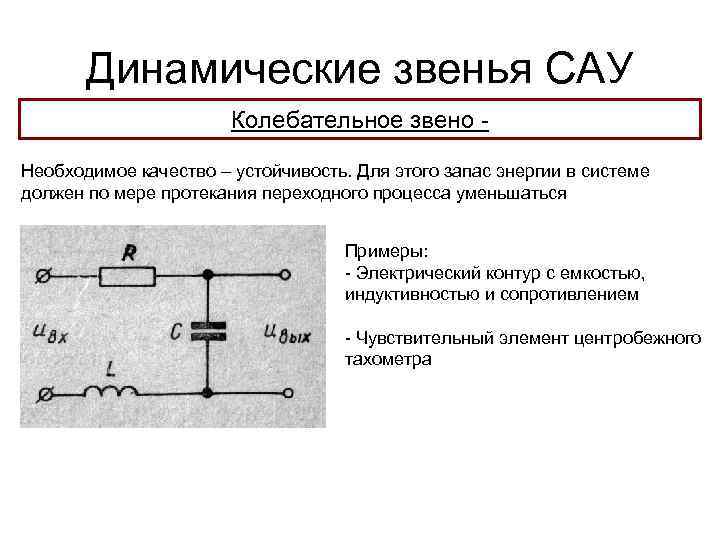Динамические звенья САУ Колебательное звено Необходимое качество – устойчивость. Для этого запас энергии в системе должен по мере протекания переходного процесса уменьшаться Примеры: - Электрический контур с емкостью, индуктивностью и сопротивлением - Чувствительный элемент центробежного тахометра

Типовые соединения звеньев Последовательное - это соединение, в котором воздействия по цепи передаются последовательно от одного звена к другому

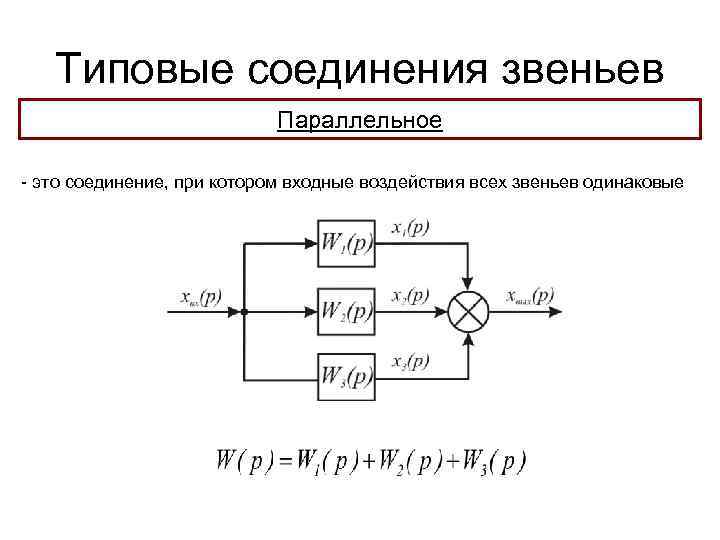Типовые соединения звеньев Параллельное - это соединение, при котором входные воздействия всех звеньев одинаковые

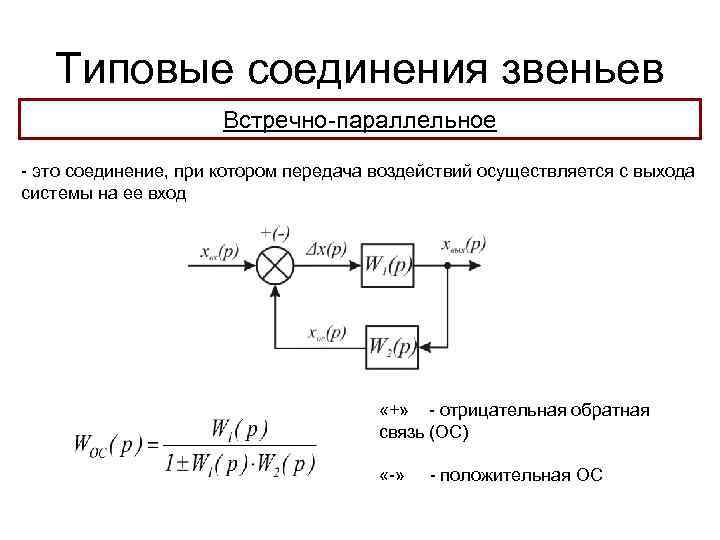Типовые соединения звеньев Встречно-параллельное - это соединение, при котором передача воздействий осуществляется с выхода системы на ее вход «+» - отрицательная обратная связь (ОС) «-» - положительная ОС

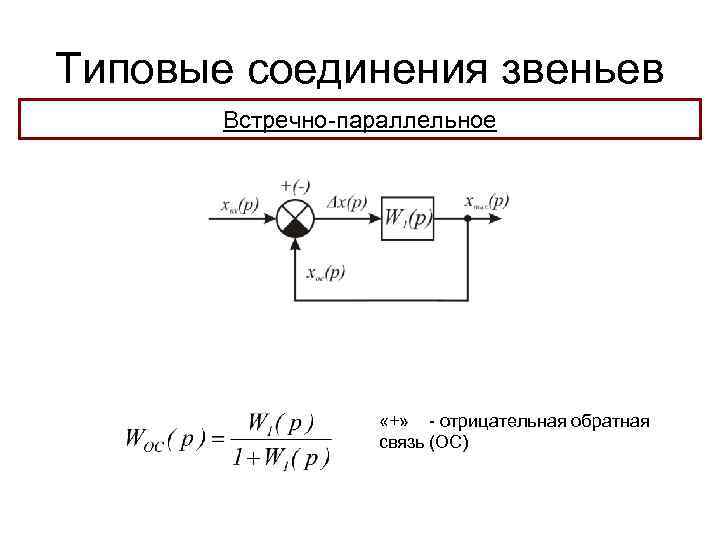Типовые соединения звеньев Встречно-параллельное «+» - отрицательная обратная связь (ОС)

Составление уравнения движения САУ Процесс непосредственного исключения промежуточных переменных при составлении общего уравнения системы, выраженного в классической форме, обычно является трудоемкой задачей. Широкое распространение получили: операторный и структурный методы Рассмотрим астатический регулятор числа оборотов непрямого действия: Пусть :

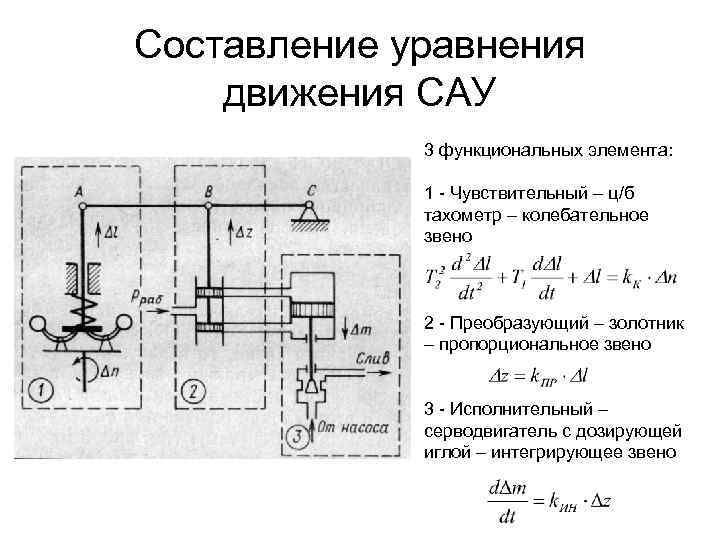Составление уравнения движения САУ 3 функциональных элемента: 1 - Чувствительный – ц/б тахометр – колебательное звено 2 - Преобразующий – золотник – пропорциональное звено 3 - Исполнительный – серводвигатель с дозирующей иглой – интегрирующее звено

Составление уравнения движения САУ Для исключения промежуточных сигналов Δl, Δz необходимо 3 -е уравнение подставить во 2 -е, а затем дважды продифференцировать, после этого подставить результат в 1 -е уравнение: В операторной форме:

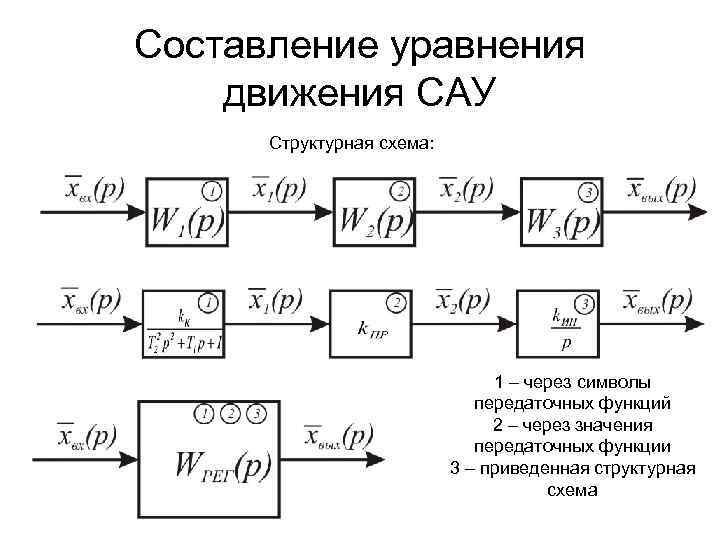Составление уравнения движения САУ Структурная схема: 1 – через символы передаточных функций 2 – через значения передаточных функции 3 – приведенная структурная схема

Составление уравнения движения САУ Структурная схема:

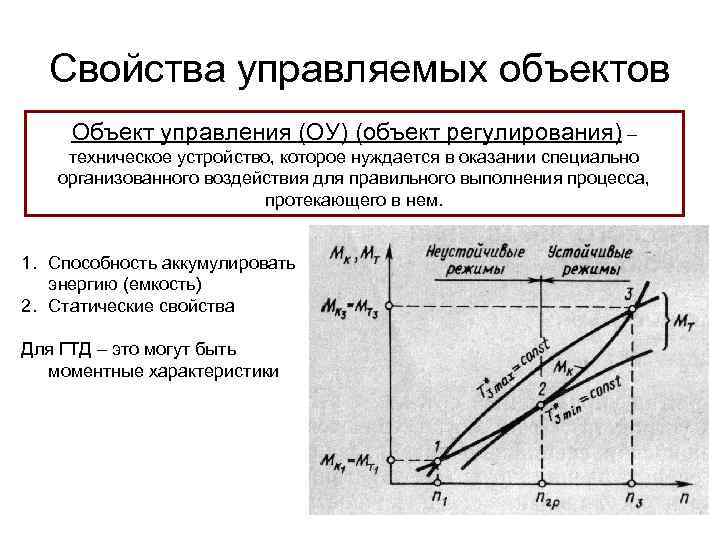Свойства управляемых объектов Объект управления (ОУ) (объект регулирования) – техническое устройство, которое нуждается в оказании специально организованного воздействия для правильного выполнения процесса, протекающего в нем. 1. Способность аккумулировать энергию (емкость) 2. Статические свойства Для ГТД – это могут быть моментные характеристики

Свойства управляемых объектов 3. Динамические свойства Для ГТД – перенастройка РУД при изменении условий полета. Необходимо знать динам. св-ва всего двигателя в предположении отсутствия у него любых САР и САУ 4. Устойчивость – способность возвращаться в исходное состояние или переходить в новое установившееся состояние после прекращения действия возмущений или сил Равновесие которое сохраняется при отклонении объекта от первоначального состояния, а само отклонение не ведет к возникновению в объекте воздействий, способных изменить это состояние называется безразличным, а сам объект носит название нейтрального

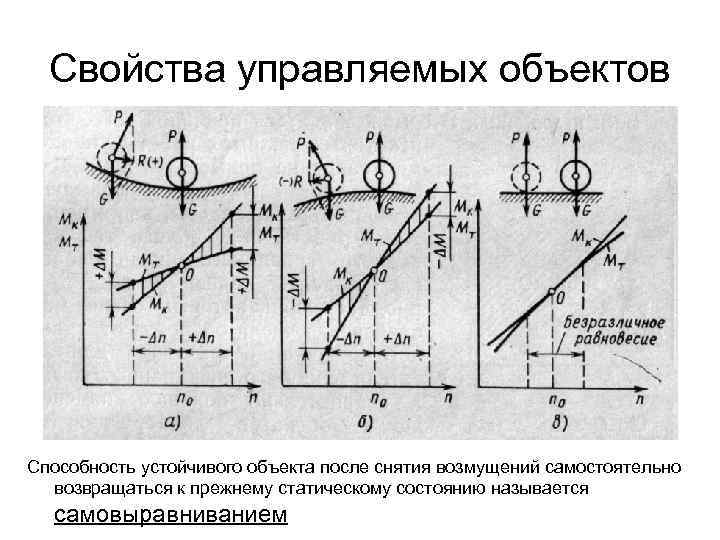Свойства управляемых объектов Способность устойчивого объекта после снятия возмущений самостоятельно возвращаться к прежнему статическому состоянию называется самовыравниванием

Устойчивость САР Форма переходного процесса определяется видом управляющего и возмущающего воздействий В общем виде уравнение движения системы имеет вид: (1) В любом звене или системе возможны вынужденное движение и свободное Уравнение свободного движения имеет вид: (2) Исследование устойчивости связано с анализом характеристического уравнения (2)

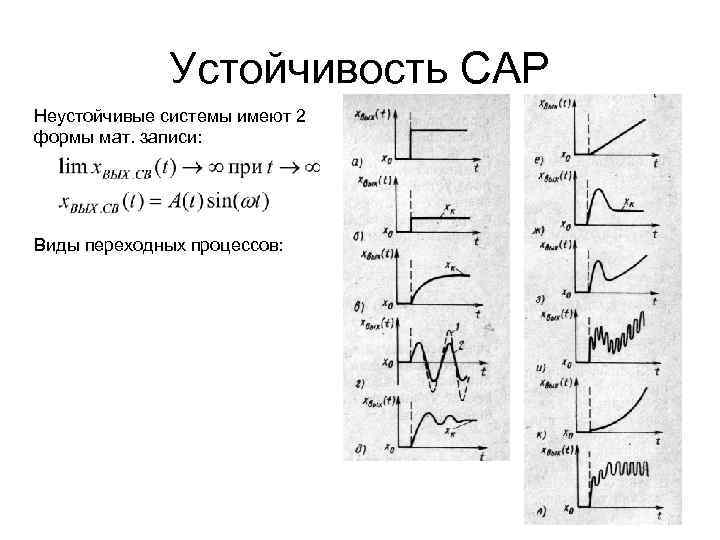Устойчивость САР Неустойчивые системы имеют 2 формы мат. записи: Виды переходных процессов:

Устойчивость простейших систем Устойчивость апериодических звеньев Пусть входное воздействие мгновенное, скачкообразное и единичное Система устойчива и устремляется монотонно к своему конечному значению =0

Устойчивость простейших систем Устойчивость апериодических звеньев С увеличением сложности систем возникает необходимость косвенного способа и метода определения устойчивости систем. А. М. Ляпуновым был предложен метод определения устойчивости САУ по знакам характеристического уравнения. Рассмотрим на примере апериодического звена: - характеристическое уравнение - решение характеристического уравнения Отрицательные корни свидетельствуют об устойчивости системы

Устойчивость простейших систем Устойчивость апериодических звеньев - характеристическое уравнение - решение характеристического уравнения Положительные корни свидетельствуют о неустойчивости системы

Устойчивость простейших систем В системах высших порядков вероятно появление иррациональных (комплексных) корней характеристического уравнения Наличие таких корней говорит о присутствии колебаний в переходном процессе: Пусть корни характеристического уравнения - Колебательный процесс без затухания - Колебательный процесс с затуханием - Расходящийся колебательный процесс

Устойчивость простейших систем Устойчивость интегрирующего звена Интегрирующее звено является неустойчивым - Передаточная функция с задержкой по времени - Характеристическое уравнение - Корень характеристического уравнения Наличие нулевых корней характеристического уравнения говорит о неустойчивости системы

Устойчивость простейших систем Устойчивость колебательного звена - Передаточная функция - Характеристическое уравнение - Корни характеристического уравнения Наличие нулевых корней характеристического уравнения говорит о неустойчивости системы - Апериодический характер (апериодическое звено 2 -го порядка); отрицательные корни - Апериодическое установление с колебательным характером переходного процесса; один корень отрицательный, другой иррациональный

Устойчивость простейших систем Устойчивость колебательного звена - Колебательный процесс без затухания; корни иррациональные - Колебательно-расходящийся процесс без затухания; один корень положительный, второй – иррациональный

Устойчивость простейших систем Выводы по устойчивости систем 1. Любое звено с неустойчивой формой переходного процесса можно с помощью дополнительных блоков и обратных связей привести к к устойчивой системе с апериодической формой переходного процесса 2. В системе, которая содержит звенья с устойчивыми переходными процессами, при наличие обратных связей могут возникнуть колебания с установившейся амплитудой или непрерывный рост параметра во времени. Такие системы становятся неустойчивыми 3. Наличие в системе звеньев только с устойчивой формой переходного процесса не служит основанием устойчивости всей системы 4. Определение устойчивости связано с определением знаков корней характеристического уравнения. Если все вещественные корни и вещественные части комплексных корней отрицательны, то система устойчива 5. Наличие комплексного корня свидетельствует о присутствии колебаний в переходном процессе

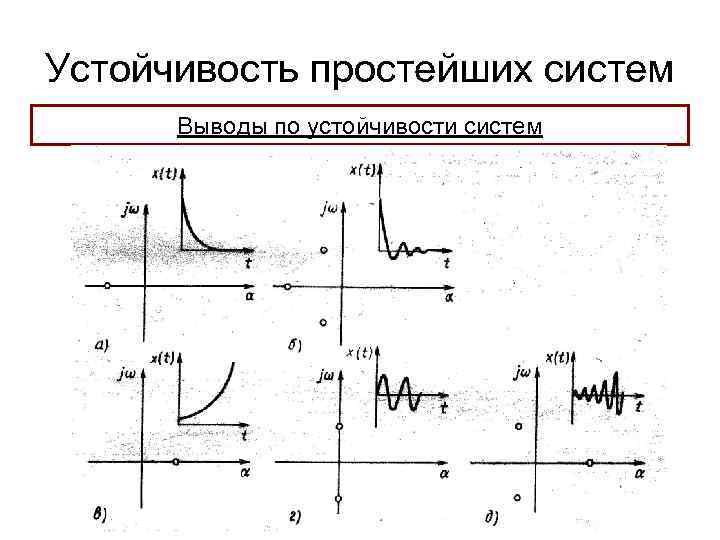Устойчивость простейших систем Выводы по устойчивости систем

Критерии устойчивости Критерий устойчивости Рауса-Гурвица Алгебраический критерий. Раус 1877 г. , Гурвиц 1895 г. Так как физические свойства системы связаны с характеристическим уравнением, то условия устойчивости можно представить в виде ряда неравенств собранных в определители Δ:

Критерии устойчивости Критерий устойчивости Рауса-Гурвица 1) Система 1 -го порядка устойчива, если: Все к-ты положительны 2) Система 2 -го порядка устойчива, если: Все к-ты положительны 3) Система 3 -го порядка устойчива, если: 4) Система 4 -го порядка устойчива, если: 5) Система 5 -го порядка устойчива, если:

Критерии устойчивости Критерий устойчивости Михайлова Метод связан с частотным анализом системы, при воздействии на нее синусоидального возмущающего сигнала с частотой ω Заменим р на j ω, тогда характеристическое уравнение примет вид: (1) При подстановке корней в характеристическое уравнение (1) оно должно обращаться в 0. Если же подставить p ≠ pk, то уравнение будет являться некоторой функцией

Критерии устойчивости Критерий устойчивости Михайлова Для системы 6 -й степени: Разделим уравнение по принципу: Получаем: Для любой точки N можно определить координаты на комплексной плоскости:

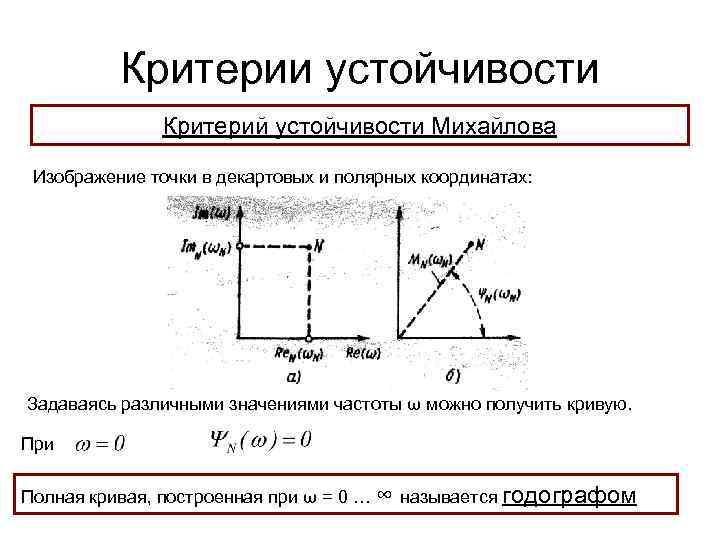Критерии устойчивости Критерий устойчивости Михайлова Изображение точки в декартовых и полярных координатах: Задаваясь различными значениями частоты ω можно получить кривую. При Полная кривая, построенная при ω = 0 … ∞ называется годографом

Критерии устойчивости Критерий устойчивости Михайлова Годограф Михайлова обладает рядом интересных свойств: 1) Линейная система n-го порядка определенно устойчива, если при изменении частоты от 0 до ∞ годограф обязательно начинается на положительной части вещественной оси, последовательно обходит против движения часовой стрелки n квадрантов и нигде не проходит через начало координат

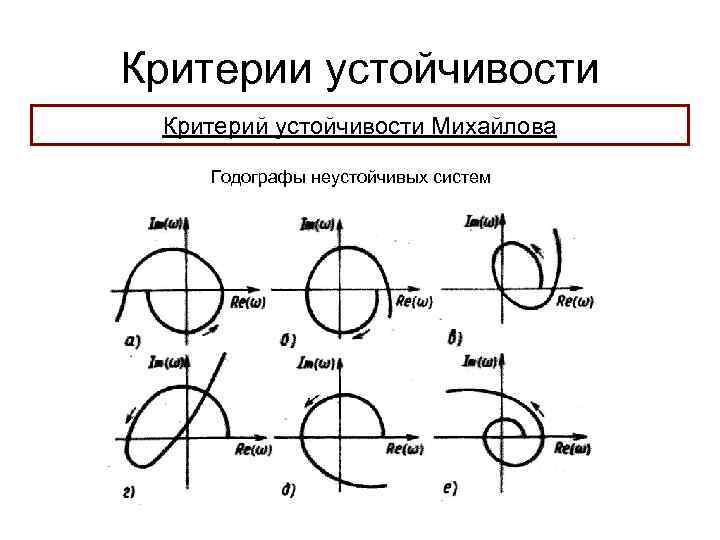Критерии устойчивости Критерий устойчивости Михайлова Годографы неустойчивых систем

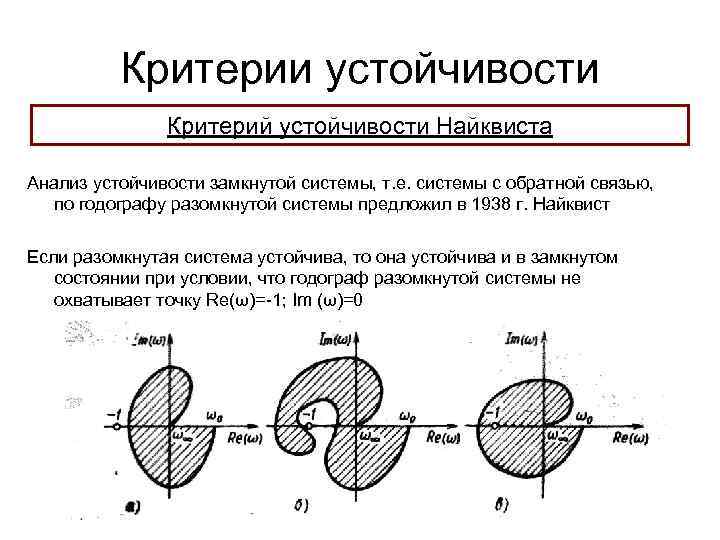Критерии устойчивости Критерий устойчивости Найквиста Анализ устойчивости замкнутой системы, т. е. системы с обратной связью, по годографу разомкнутой системы предложил в 1938 г. Найквист Если разомкнутая система устойчива, то она устойчива и в замкнутом состоянии при условии, что годограф разомкнутой системы не охватывает точку Re(ω)=-1; Im (ω)=0

Критерии устойчивости Критерий устойчивости Найквиста Неустойчивая разомкнутая система при обхвате обратной связью может стать устойчивой. Для этого случая существует специальное условие: Если разомкнутая система неустойчива, то она устойчива в замкнутом состоянии при условии, что годограф разомкнутой системы, дополненный вспомогательной дугой, не охватывает точку Re(ω)=-1; Im (ω)=0 Вспомогательная дуга проводится от точки, лежащей на положительной части вещественной оси по часовой стрелке до пересечения с годографом в последнем квадранте при ωi = 0

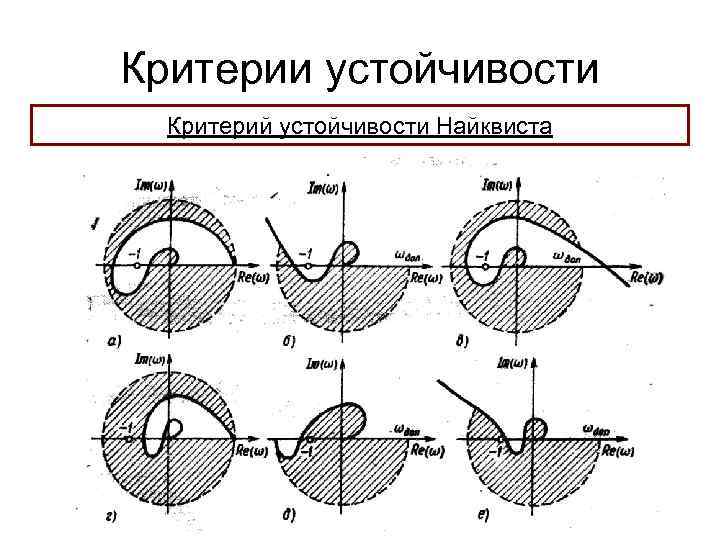Критерии устойчивости Критерий устойчивости Найквиста

Области устойчивости Устойчивость зависит от выбора входящих в систему элементов и их параметров. Отдельные конструктивные решения или даже тип пружин или амортизирующих жидкостей, масса движущихся частей, размеры соединительных каналов и параметры механических, гидравлических, пневматических деталей радиотехнических элементов (сопротивлений, конденсаторов, индуктивностей, транзисторов, диодов и др. ) влияют на вид переходного процесса и на устойчивость. Количество параметров частей САУ может быть довольно велико и необходимо проанализировать их сочетание и устойчивость всей системы Для этого определяют не отдельные значения параметров, а области их значений, при которых вся система устойчива Обычно области устойчивости изображают графически

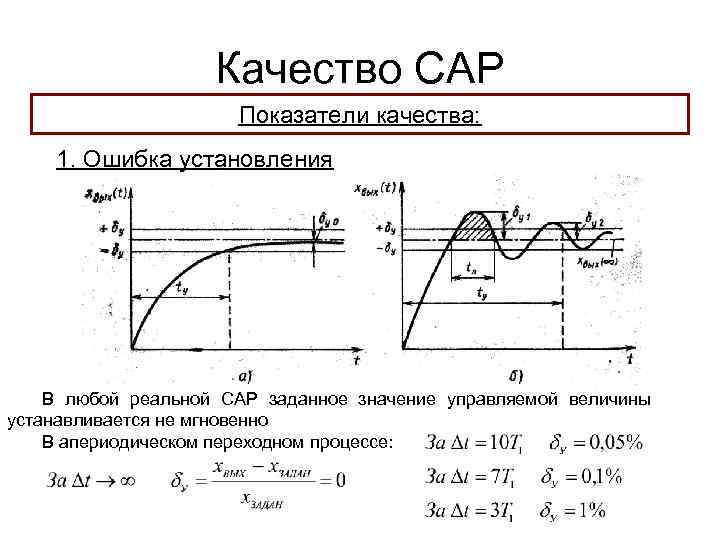Качество САР Показатели качества: 1. Ошибка установления В любой реальной САР заданное значение управляемой величины устанавливается не мгновенно В апериодическом переходном процессе:

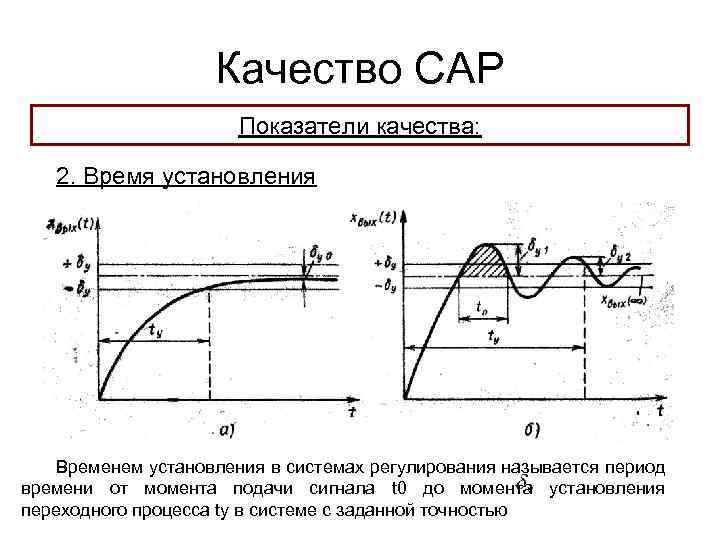Качество САР Показатели качества: 2. Время установления Временем установления в системах регулирования называется период времени от момента подачи сигнала t 0 до момента установления переходного процесса ty в системе с заданной точностью

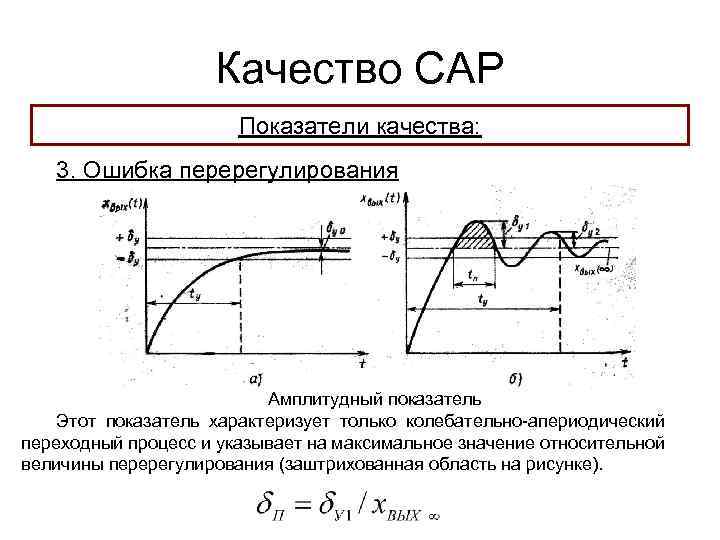Качество САР Показатели качества: 3. Ошибка перерегулирования Амплитудный показатель Этот показатель характеризует только колебательно-апериодический переходный процесс и указывает на максимальное значение относительной величины перерегулирования (заштрихованная область на рисунке).

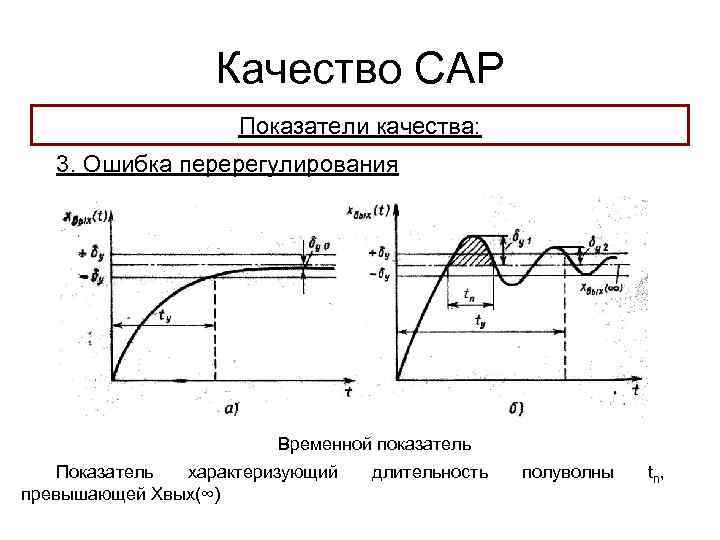Качество САР Показатели качества: 3. Ошибка перерегулирования Временной показатель Показатель характеризующий превышающей Хвых(∞) длительность полуволны tn ,

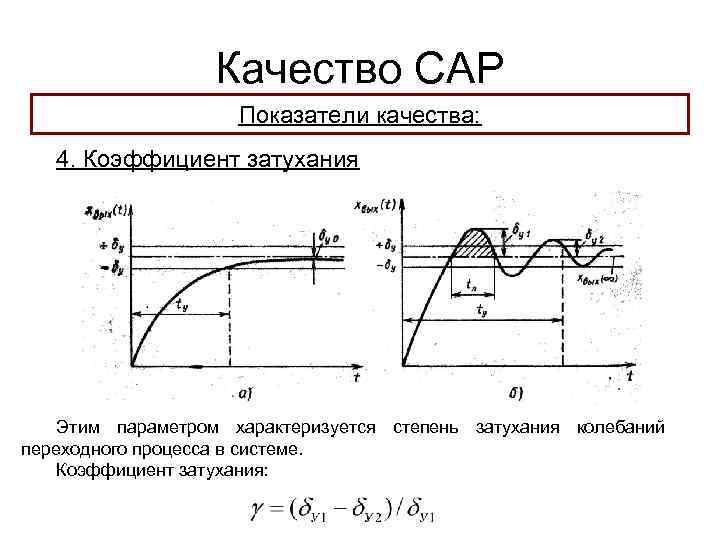Качество САР Показатели качества: 4. Коэффициент затухания Этим параметром характеризуется степень затухания колебаний переходного процесса в системе. Коэффициент затухания:

Качество САР Показатели качества: 5. Интегральный показатель качества Обобщенный критерий качества В основу критерия положено количественное определение близости прохождения кривой переходного процесса Xвых(t) от идеальной Хвых(∞) за время от t = 0 до t = ∞ (или t = tу) Для апериодического процесса:

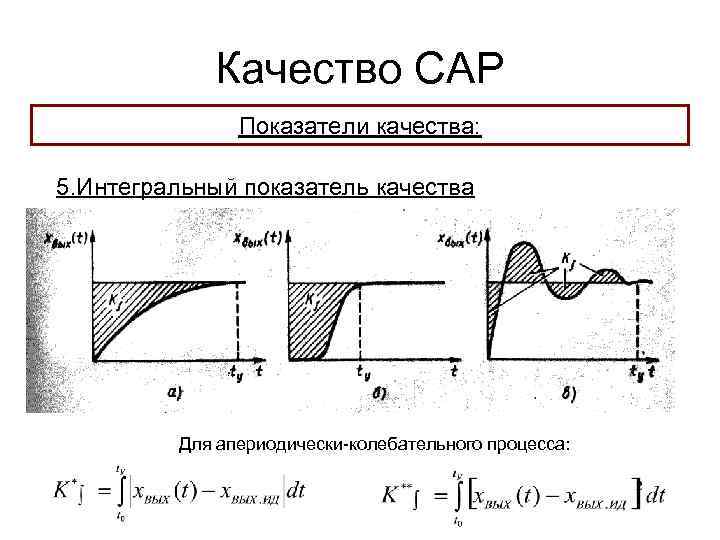Качество САР Показатели качества: 5. Интегральный показатель качества Для апериодически-колебательного процесса:

Качество САР Диаграммы переходных процессов: Вышнеградский, 1874 г. – первая диаграмма переходных процессов и устойчивости для систем регулирования 3 -го порядка Для этого уравнение 3 -го порядка с 4 -мя коэффициентами было заменено на уравнение 3 -го порядка с 2 -мя коэффициентами: Задавая В 1 и В 2 и анализируя корни характеристического уравнения можно построить диаграмму Такой метод оценки качества (устойчивости) еще называют корневым

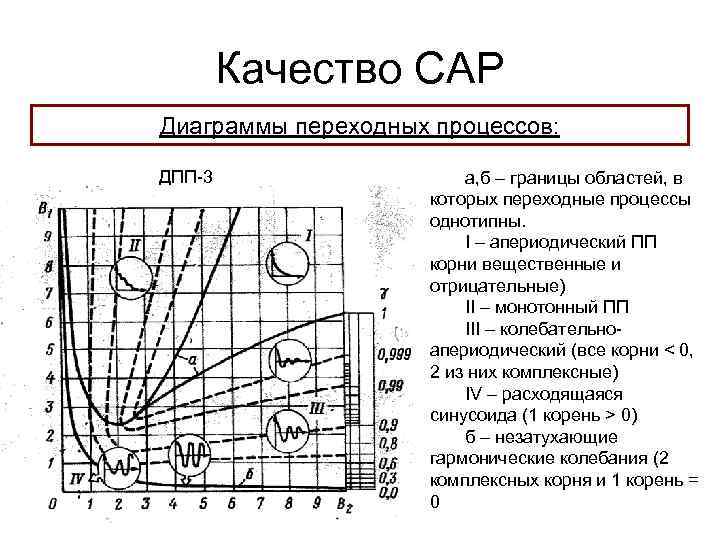Качество САР Диаграммы переходных процессов: ДПП-3 а, б – границы областей, в которых переходные процессы однотипны. I – апериодический ПП корни вещественные и отрицательные) II – монотонный ПП III – колебательноапериодический (все корни < 0, 2 из них комплексные) IV – расходящаяся синусоида (1 корень > 0) б – незатухающие гармонические колебания (2 комплексных корня и 1 корень = 0

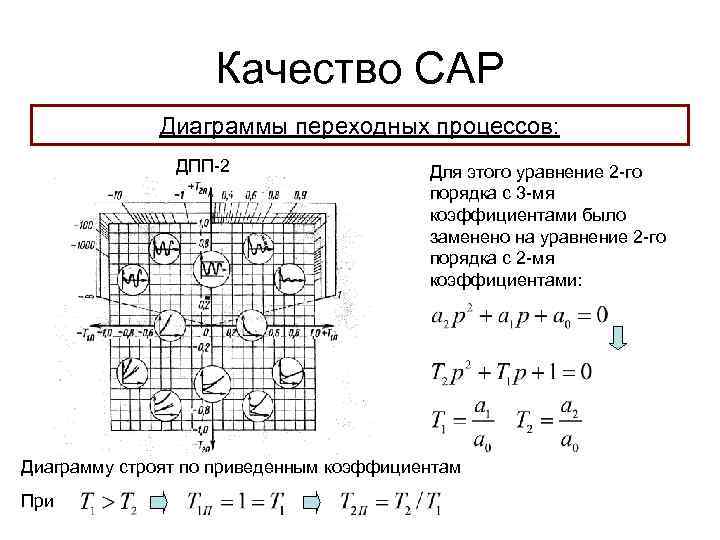Качество САР Диаграммы переходных процессов: ДПП-2 Для этого уравнение 2 -го порядка с 3 -мя коэффициентами было заменено на уравнение 2 -го порядка с 2 -мя коэффициентами: Диаграмму строят по приведенным коэффициентам При

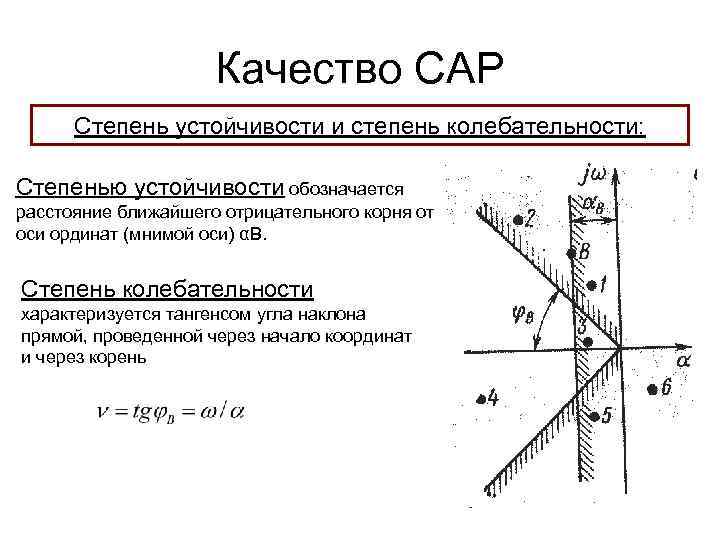Качество САР Степень устойчивости и степень колебательности: Степенью устойчивости обозначается раcстояние ближайшего отрицательного корня от оси ординат (мнимой оси) αB. Степень колебательности характеризуется тангенсом угла наклона прямой, проведенной через начало координат и через корень

Качество САР Запасы основных показателей системы: При проектировании САР необходимо определять запасы устойчивости, колебательности и т. д. Оценку запаса проводят в абсолютном и относительном виде: Абсолютное значение запаса указывает, насколько далек показатель исследуемой системы от границы допустимого значения. Относительная форма записи: Относительное значение запаса указывает, во сколько раз показатель исследуемой системы «лучше» заданного показателя

Качество САР Запасы основных показателей системы: Запасы устойчивости по амплитуде: Система будет устойчива и в замкнутом состоянии, если годограф АФЧХ разомкнутой системы не охватывает точку Re = -1; Im = 0. Чем дальше проходит линия годографа от этой точки, тем система устойчивее. Запасом устойчивости САР по модулю (по амплитуде) называют расстояние q от точки годографа, при пересечении оси абсцисс, до точки (Re = -1; Im = 0) – границы устойчивости.

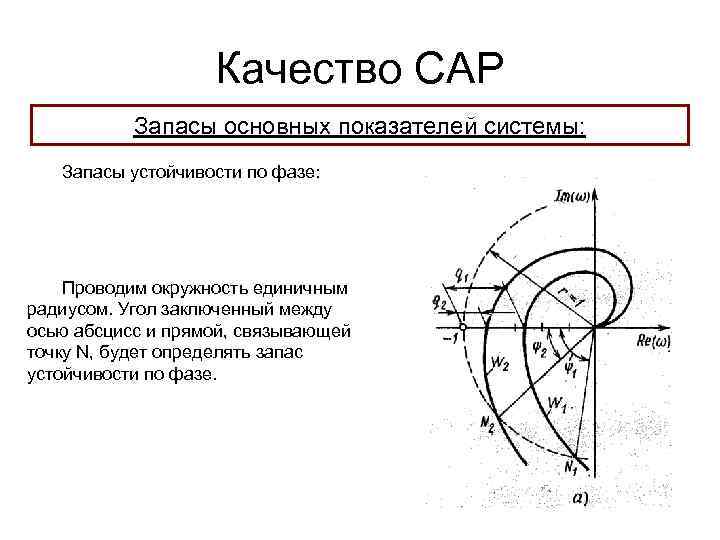Качество САР Запасы основных показателей системы: Запасы устойчивости по фазе: Проводим окружность единичным радиусом. Угол заключенный между осью абсцисс и прямой, связывающей точку N, будет определять запас устойчивости по фазе.

Качество САР Запасы основных показателей системы: Запас системы по степени колебательности: Система характеризуется степенью колебательности или коэффициентом затухания. Завышенное значение коэффициента затухания нежелательно и приводит к к ухудшению динамических свойств системы, а завышенное к ухудшению других качественных показателей (время установления, ошибка перерегулирования, интегральные оценки и т. д. ) Запас по степени колебательности определяется с помощью диаграмм переходных процессов.

Улучшение качества САР Структурные методы улучшения: Качество может быть улучшено применением блоков различных типов Основной блок – это блок, реализующий основную операцию регулирования Вспомогательный блок – это блок, который улучшает качество основного блока Общая передаточная функция САР определяется правилом соединения звеньев. При последовательно-параллельном соединении обратная связь с выхода основного блока идет на вход через вспомогательный блок. Обратная связь может быть отрицательной (ООС) и положительной (ПОС) Положительная, когда знак входного сигнала совпадает со знаком обратной связи; оба сигнала суммируются. Отрицательная – сигналы вычитаются.

Улучшение качества САР Структурные методы улучшения: Наиболее часто в последовательном соединении с основным блоком включают пропорциональное, апериодическое или интегрирующее звено. В параллельных соединениях – пропорциональное, дфференцирующее или интегро-дифференцирующее звено. В параллельно-последовательных – пропорциональное, дифференцирующее или апериодическое звено. Такие соединения для улучшения качества САР назовем структурами коррекции

Улучшение качества САР Уменьшение статической ошибки: Рассмотрим 3 метода уменьшения статической ошибки на примере пропорционального звена: В реальном звене сложно получить стабильный коэффициент передачи, вследствие влияния различных внешних факторов, например, колебание температуры окружающей среды, радиоактивного излучения, вибрации и т. д.

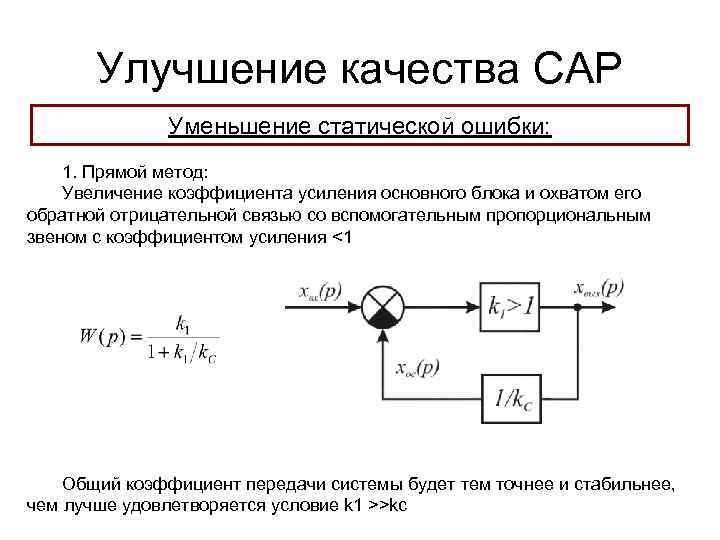Улучшение качества САР Уменьшение статической ошибки: 1. Прямой метод: Увеличение коэффициента усиления основного блока и охватом его обратной отрицательной связью со вспомогательным пропорциональным звеном с коэффициентом усиления <1 Общий коэффициент передачи системы будет тем точнее и стабильнее, чем лучше удовлетворяется условие k 1 >>kc

Улучшение качества САР Уменьшение статической ошибки: Пример действия метода: Определить коэффициент передачи системы. k 1 = 90 -110 (нестабильность - 10%), kc = 5. Если принять W(p)=5, то погрешность – 4, 4… 5, 2%, нестабильность 0, 8% С увеличением k 1 в 10 раз, ошибка уменьшится до 0, 46… 0, 56%

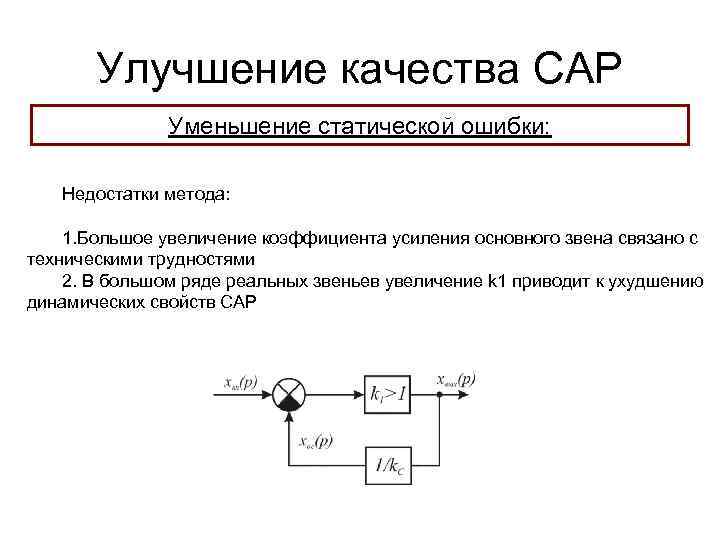Улучшение качества САР Уменьшение статической ошибки: Недостатки метода: 1. Большое увеличение коэффициента усиления основного звена связано с техническими трудностями 2. В большом ряде реальных звеньев увеличение k 1 приводит к ухудшению динамических свойств САР

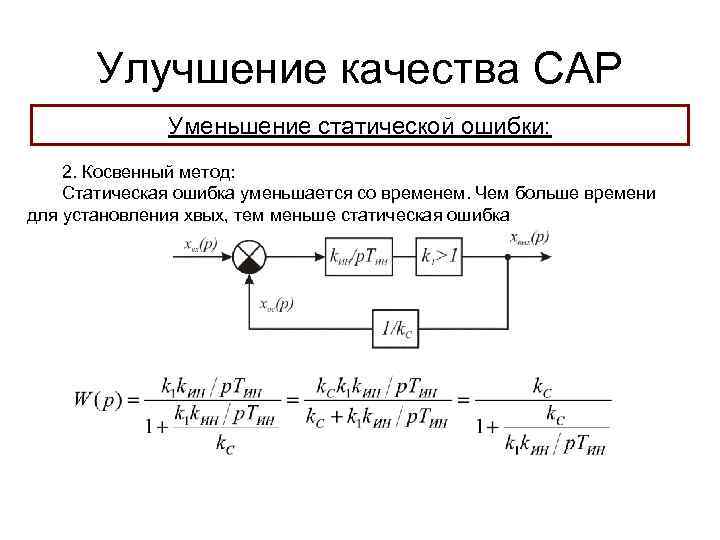Улучшение качества САР Уменьшение статической ошибки: 2. Косвенный метод: Статическая ошибка уменьшается со временем. Чем больше времени для установления хвых, тем меньше статическая ошибка

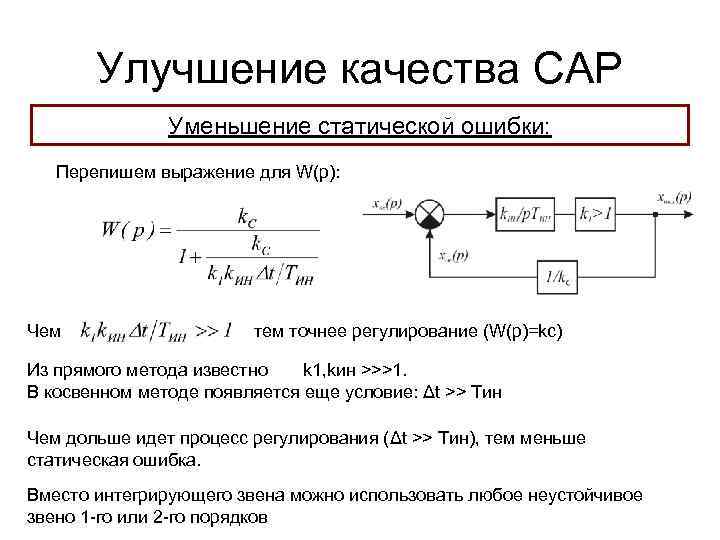Улучшение качества САР Уменьшение статической ошибки: Перепишем выражение для W(p): Чем точнее регулирование (W(p)=kc) Из прямого метода известно k 1, kин >>>1. В косвенном методе появляется еще условие: Δt >> Tин Чем дольше идет процесс регулирования (Δt >> Tин), тем меньше статическая ошибка. Вместо интегрирующего звена можно использовать любое неустойчивое звено 1 -го или 2 -го порядков

Улучшение качества САР Уменьшение статической ошибки: Пример действия метода: Определить стат. ошибку системы при k = k 1*kин = 90, kc = 5, Δt =Tин. Если принять W(p)=5, то погрешность – 5, 2% При Δt =3 Tин, погрешность 1, 8%, 3 -х кратное уменьшение стат. ошибки

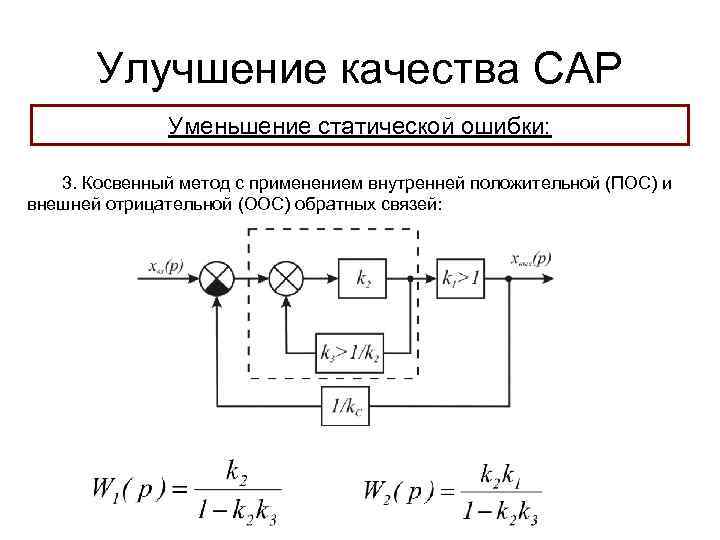Улучшение качества САР Уменьшение статической ошибки: 3. Косвенный метод с применением внутренней положительной (ПОС) и внешней отрицательной (ООС) обратных связей:

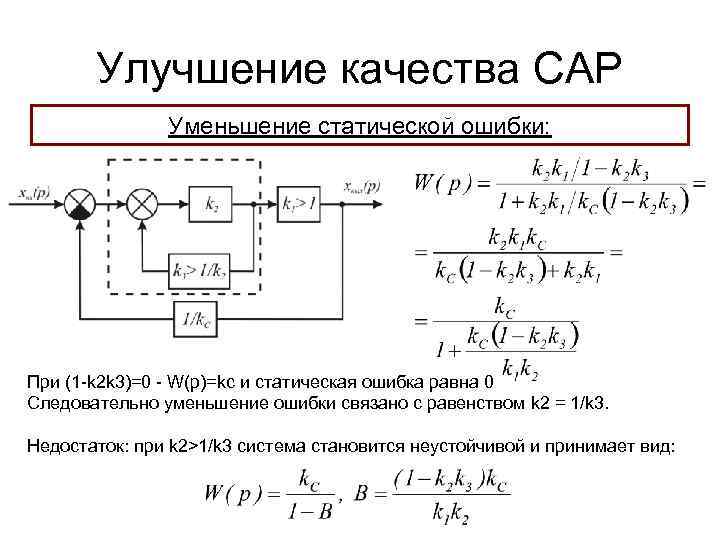Улучшение качества САР Уменьшение статической ошибки: При (1 -k 2 k 3)=0 - W(p)=kc и статическая ошибка равна 0 Следовательно уменьшение ошибки связано с равенством k 2 = 1/k 3. Недостаток: при k 2>1/k 3 система становится неустойчивой и принимает вид:

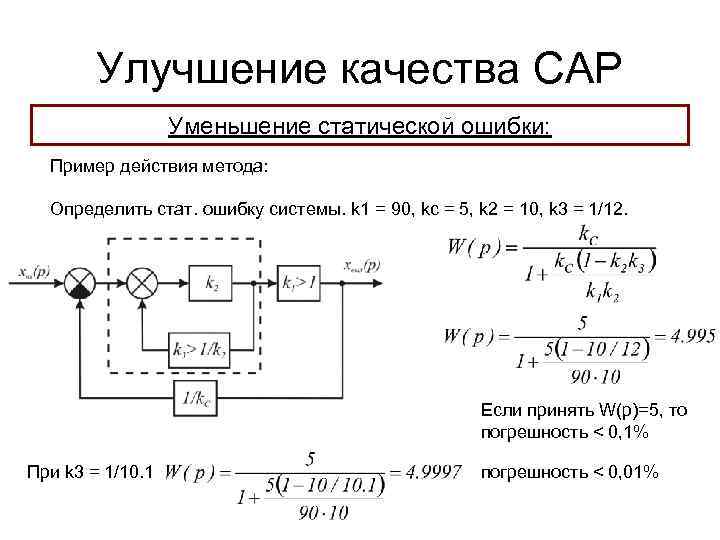Улучшение качества САР Уменьшение статической ошибки: Пример действия метода: Определить стат. ошибку системы. k 1 = 90, kc = 5, k 2 = 10, k 3 = 1/12. Если принять W(p)=5, то погрешность < 0, 1% При k 3 = 1/10. 1 погрешность < 0, 01%

Улучшение качества САР Коррекция динамических свойств: Для замкнутых систем повышение качества регулирования в установившемся режиме часто входит в противоречие с качеством регулирования в переходном процессе Для уменьшения статической ошибки часто приходится увеличивать коэффициент усиления основного блока, что может привести к изменению запаса устойчивости системы. Чтобы сохранить запас устойчивости и улучшить показатели качества переходного процесса необходимо изменить частотные (динамические) характеристики САР или осуществить коррекцию САР

Улучшение качества САР Коррекция динамических свойств: Под коррекцией САР понимается изменение динамических свойств (характеристик) с целью обеспечения требуемого запаса устойчивости, повышения динамической точности и показателей качества переходного процесса. Для коррекции САР в систему включают дополнительные корректирующие звенья (корректирующие устройства) Различают 4 вида корректирующих устройств (КУ): 1. 2. 3. 4. Последовательные (корректирующие фильтры) Параллельные По внешнему воздействию Неединичная главная обратная связь

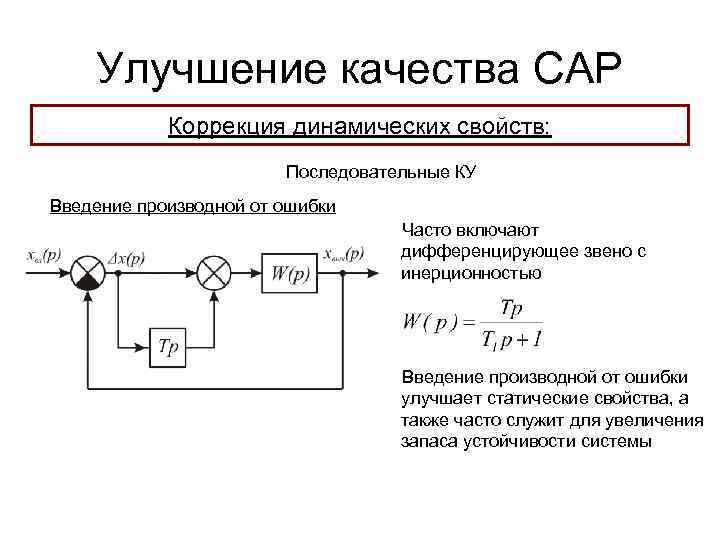Улучшение качества САР Коррекция динамических свойств: Последовательные КУ Введение производной от ошибки Часто включают дифференцирующее звено с инерционностью Введение производной от ошибки улучшает статические свойства, а также часто служит для увеличения запаса устойчивости системы

Улучшение качества САР Коррекция динамических свойств: Последовательные КУ Введение производной от ошибки В этом случае добавляется еще одна фаза (ФЧХ доворачивается еще на 1 квадрант, что увеличивает запас по фазе Запас устойчивости системы также увеличивается При введении дифференцирующего звена с инерционностью качественно перечисленные эффекты сохраняются, при некотором снижении количественных показателей

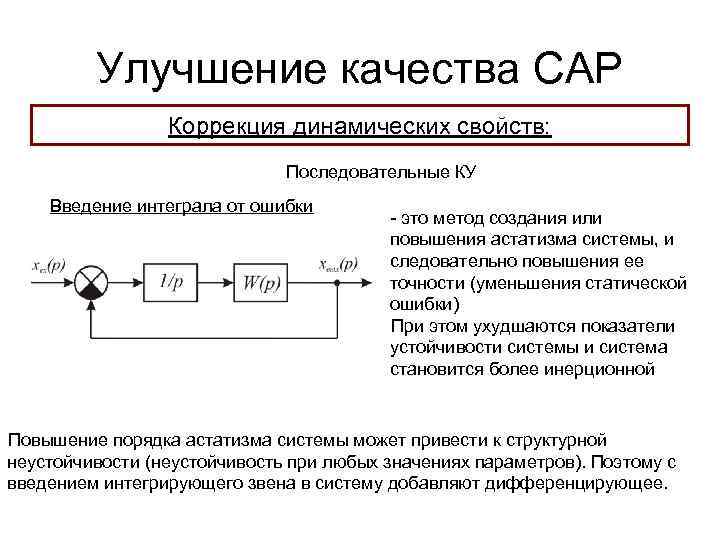Улучшение качества САР Коррекция динамических свойств: Последовательные КУ Введение интеграла от ошибки - это метод создания или повышения астатизма системы, и следовательно повышения ее точности (уменьшения статической ошибки) При этом ухудшаются показатели устойчивости системы и система становится более инерционной Повышение порядка астатизма системы может привести к структурной неустойчивости (неустойчивость при любых значениях параметров). Поэтому с введением интегрирующего звена в систему добавляют дифференцирующее.

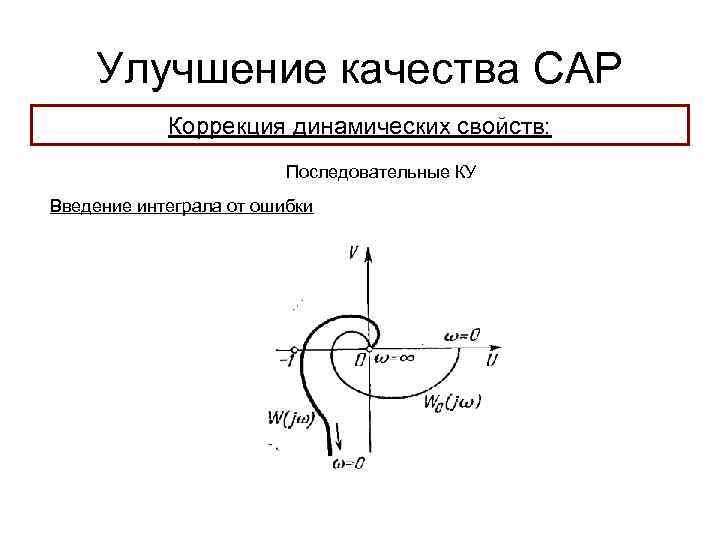Улучшение качества САР Коррекция динамических свойств: Последовательные КУ Введение интеграла от ошибки

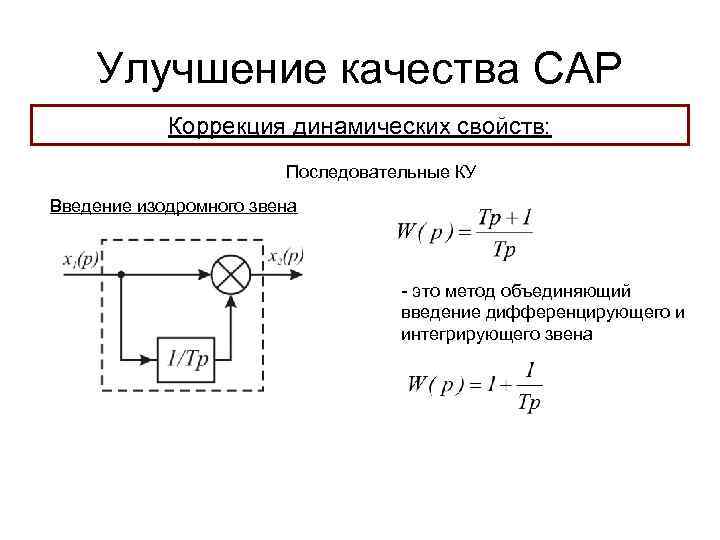Улучшение качества САР Коррекция динамических свойств: Последовательные КУ Введение изодромного звена - это метод объединяющий введение дифференцирующего и интегрирующего звена

Улучшение качества САР Коррекция динамических свойств: Параллельные КУ 1. Жесткая обратная связь (ЖОС) 2. Инерционная жесткая обратная связь 3. Гибкая обратная связь (ГОС) 4. Инерционная гибкая обратная связь

Улучшение качества САР Коррекция динамических свойств: Параллельные КУ Положительная ЖОС Служит для увеличения коэффициента усиления системы. Однако при этом возрастает инерционность (Т 1). При koc > 1/k система становится неустойчивой

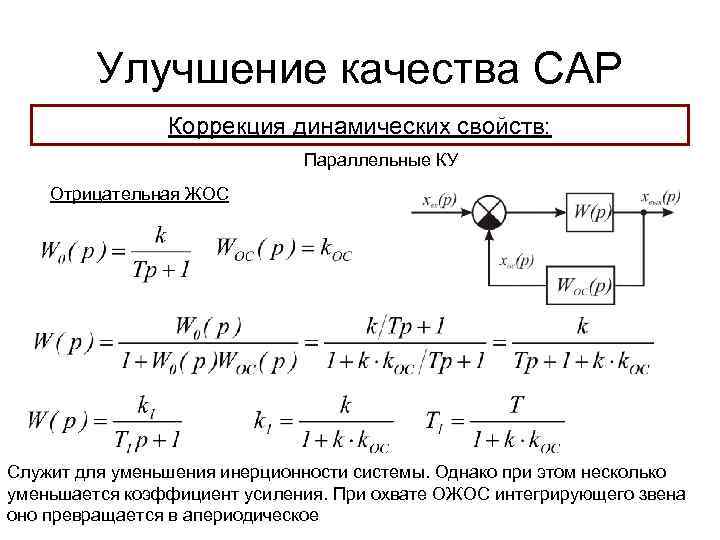Улучшение качества САР Коррекция динамических свойств: Параллельные КУ Отрицательная ЖОС Служит для уменьшения инерционности системы. Однако при этом несколько уменьшается коэффициент усиления. При охвате ОЖОС интегрирующего звена оно превращается в апериодическое

Улучшение качества САР Коррекция динамических свойств: Параллельные КУ Инерционная ЖОС Интегрирующее звено превращается в звено 2 -го порядка с введением производной. При этом к-т усиления k 1 и интенсивность введения производной Тос определяются обратной связью, а k влияет на постоянные времени Т 1 и Т 2. Чем > k тем < T 1, T 2. При k>>>1, система превращается в усилительное звено с производной, что дает хорошие динамические характеристики.

Улучшение качества САР Коррекция динамических свойств: Параллельные КУ ГОС В этом случае увеличивается к-т демпфирования системы, при неизменном к-те усиления

Улучшение качества САР Коррекция динамических свойств: Параллельные КУ ГОС При охвате апериодического звена ГОС увеличивается его инерционность. При охвате инерционного интегрирующего звена – инерционность уменьшается:

Улучшение качества САР Коррекция динамических свойств: Параллельные КУ Инерционная ГОС При охвате инерционного интегрирующего звена : При малых Т 1, Т 2 звено становится изодромным, при сохранении его интегрирующих свойств (астатизм системы). Введение в обратную связь звеньев с запаздыванием аналогично введению производной в прямой цепи. При этом ЖОС аннулируют астатизм, а ГОС сохраняют

САУ ГТД как объект регулирования: Рассмотрим ТРД с неизменяемой геометрией проточной части ГТД – это сложная динамическая система с несколькими аккумуляторными емкостями энергии. Процессы, протекающие в двигателе, зависят от множества факторов, и поэтому число диф. уравнений может превышать 15. Практика показывает, что главными факторами являются: 1. Инерционность ротора 2. Скорость изменения давления рабочего тела в пространстве между ОК и ГТ 3. Скорость изменения температуры в КС. В первом приближении учитывают только инерционность ротора

САУ ГТД как объект регулирования: Тогда диф. уравнение ТРД: Уравнение показывает зависимость угловой скорости вращения ротора по времени t (угловое ускорение) от величины избыточного крутящего момента ротора ΔМ при его собственных инерционных свойствах, выраженных моментом инерции I. Крутящий момент ГТ и момент сопротивления ОК зависят от числе оборотов двигателя, подачи топлива и внешней нагрузки на ротор. Моментами, необходимыми для привода агрегатов и преодоления сил трения пренебрегаем. Выведем уравнение движения для ТРД:

САУ ГТД как объект регулирования: Допущения при выводе: 1. Внешние воздействия отсутствуют 2. Топливный насос имеет независимый от ротора ТРД автономный привод, что обеспечивает постоянную подачу топлива вне зависимости от числа оборотов. 3. Рассматриваем динамику работу ТРД при малых отклонениях n и GT Эксперимент показывает что при постоянных подачах топлива GT=GT 0=const (с увеличением числа оборотов) и при n=n 0=const (с увеличением подачи топлива) моменты МТ и МК изменяются по сложным нелинейным законам

САУ ГТД как объект регулирования: Поскольку функции и то для решения диф. уравнения движения необходимо провести их линеаризацию нелинейны,

Нелинейные САУ Понятие о нелинейных системах: Нелинейной системой называется система, описываемая нелинейными дифференциальными уравнениями а) релейная характеристика б) характеристика кусочно-линейного типа в) криволинейная характеристика произвольного вида г) с логической операцией

Нелинейные САУ Понятие о нелинейных системах: Процессы в нелинейных системах имеют ряд особенностей: 1. Начальные условия могут влиять на устойчивость. 2. Возможен новый вид установившегося режима – автоколебания 3. Неприменим метод суперпозиции Протекание процессов регулирования в нелинейных системах может быть найдено методом припасовывания (сшивания). Метод заключается в разбиении функции на участки, в которых процесс описывается линейным диф. уравнением. Для того, чтобы привести нелинейные диф. уравнения к линейным используют процедуру линеаризации.

Линеаризация характеристик Понятие о линеаризации характеристик Линеаризацию применяют также для приближенного решения дифференциальных уравнений. Если участок нелинейной характеристики плавно изменяющийся, а отклонения входных и выходных переменных на нем малы, то этот участок кривой можно заменить касательной, проведенной к ней в точке, соответствующей исходному статическому режиму. Такая операция носит название линеаризации Линеаризация может быть графической и аналитической.

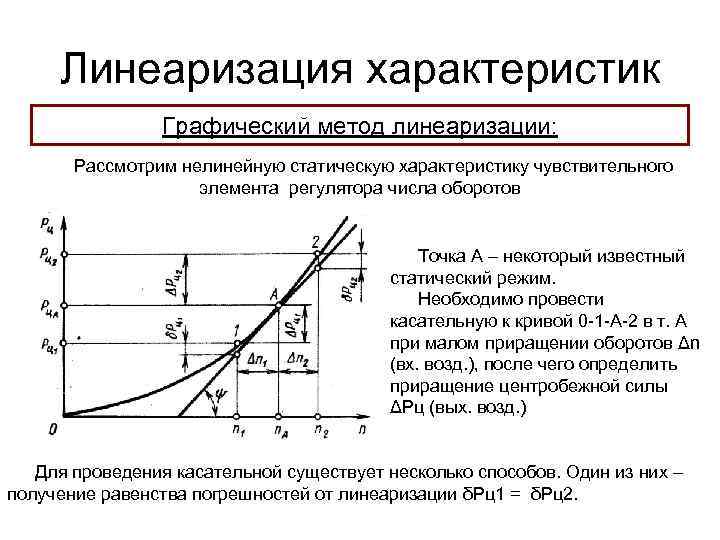Линеаризация характеристик Графический метод линеаризации: Рассмотрим нелинейную статическую характеристику чувствительного элемента регулятора числа оборотов Точка А – некоторый известный статический режим. Необходимо провести касательную к кривой 0 -1 -А-2 в т. А при малом приращении оборотов Δn (вх. возд. ), после чего определить приращение центробежной силы ΔРц (вых. возд. ) Для проведения касательной существует несколько способов. Один из них – получение равенства погрешностей от линеаризации δPц1 = δPц2.

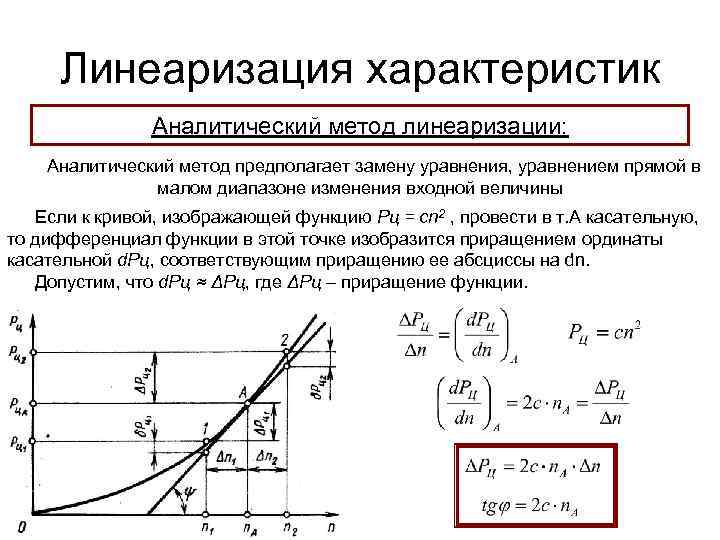Линеаризация характеристик Аналитический метод линеаризации: Аналитический метод предполагает замену уравнения, уравнением прямой в малом диапазоне изменения входной величины Если к кривой, изображающей функцию Рц = cn 2 , провести в т. А касательную, то дифференциал функции в этой точке изобразится приращением ординаты касательной d. Pц, соответствующим приращению ее абсциссы на dn. Допустим, что d. Pц ≈ ΔPц, где ΔPц – приращение функции.

Метод фазовой плоскости В некоторых случаях систему нельзя рассматривать в линеаризованном виде. В этих случаях применяют специальные методы для расчета САУ, с учетом нелинейностей. Допустим, что совокупность уравнений, описывающих систему n-го порядка, может быть представлена в виде n уравнений первого порядка: - независимые переменные, определяющие состояние системы - управляющее и возмущающее воздействия

Метод фазовой плоскости Каждому состоянию системы соответствуют определенные значения независимых переменных. Эти переменные можно представить в виде прямоугольных координат некоторой точки М, которую назовем изображающей точкой. Если с течением времени происходит изменение независимых координат, то координаты изображающей точки также будут меняться, а сама она будет перемещаться в выбранной системе координат, прочерчивая кривую, называемую фазовой траекторией Направление движения обозначается на фазовой траектории стрелками Пространство, в котором движется точка М, называется фазовым пространством

Метод фазовой плоскости В системе 2 -го порядка будут только 2 независимые переменные x 1 и х2. В этом случае фазовое пространство превращается в фазовую плоскость. Фазовые траектории дают качественную оценку протекания процессов в нелинейных системах, поскольку не включают в себя время. Для построения фазовой траектории для системы 2 -го порядка используется прямоугольная система координат. По оси абсцисс откладывается х1, по оси ординат ее производная х`1 Начало координат фазовой плоскости, является – особой точкой и называется устойчивым фокусом (неустойчивым фокусом)

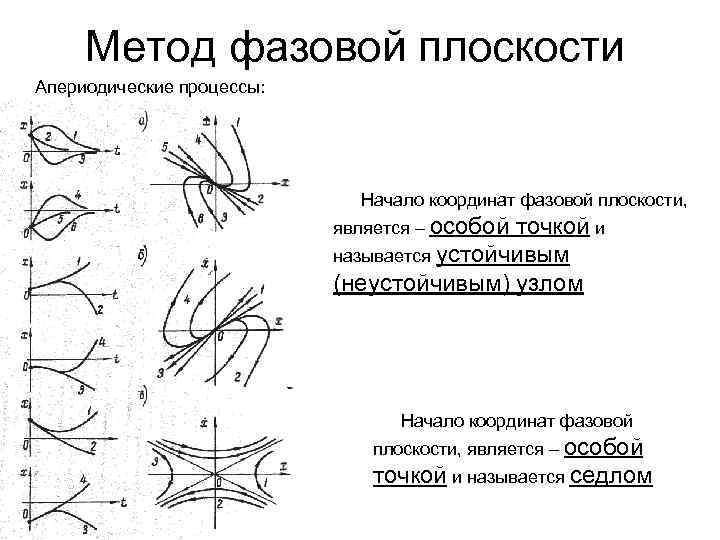Метод фазовой плоскости Апериодические процессы: Начало координат фазовой плоскости, является – особой точкой и называется устойчивым (неустойчивым) узлом Начало координат фазовой плоскости, является – особой точкой и называется седлом

Метод фазовой плоскости Периодический колебательный процесс: Начало координат фазовой плоскости, является – особой называется центром точкой и

Метод фазовой плоскости Особые линии: особая точка в системе с зоной нечувствительности превращается в особый отрезок Возможна ситуация когда на фазовой плоскости существует замкнутая фазовая траектория, к которой стремятся все остальные фазовые траектории. Такая замкнутая кривая называется устойчивым предельным циклом Все ф. траектории находящиеся внутри предельного цикла соответствуют расходящемуся процессу и в пределе сливаются с предельным циклом. Траектории снаружи – наоборот соответствуют сходящемуся процессу

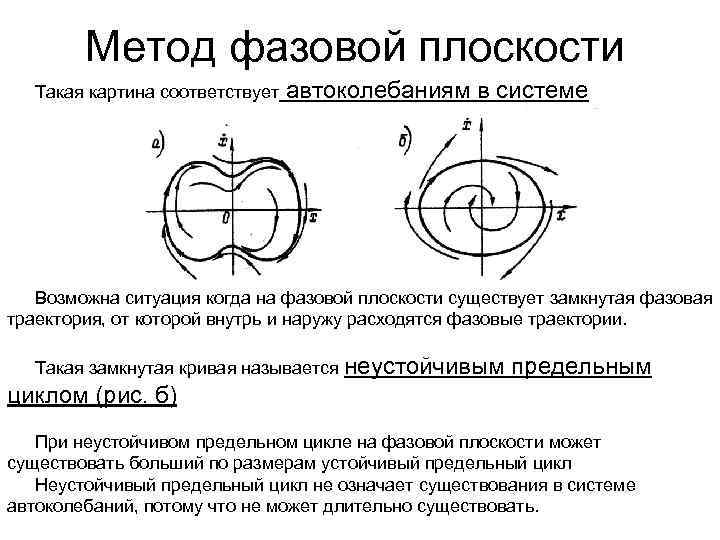Метод фазовой плоскости Такая картина соответствует автоколебаниям в системе Возможна ситуация когда на фазовой плоскости существует замкнутая фазовая траектория, от которой внутрь и наружу расходятся фазовые траектории. Такая замкнутая кривая называется неустойчивым предельным циклом (рис. б) При неустойчивом предельном цикле на фазовой плоскости может существовать больший по размерам устойчивый предельный цикл Неустойчивый предельный цикл не означает существования в системе автоколебаний, потому что не может длительно существовать.

Гармоническая линеаризация Рассмотрим нелинейную систему, которую можно разбить на линейную часть и нелинейное звено Уравнение линейной части: Уравнение нелинейного звена: На вход в нелинейное звено поступает гармонический сигнал: Подставим в нелинейную функцию и разложим в ряд Фурье:

Гармоническая линеаризация Предположим, что в искомых колебаниях отсутствует постоянная составляющая, т. е. нелинейная характеристика симметрична относительно системы координат: Произведем замену: Отбросим все высшие гармоники, считая, что линейная часть – это фильтр верхних частот. Тогда: где ряд Фурье - коэффициенты, определяемые формулами разложения в

Гармоническая линеаризация Операция замены нелинейного уравнения приближенным линейным называется гармонической линеаризацией, а к-ты q и q` называются гармоническими коэффициентами передачи нелинейного звена. Получаем передаточную функцию разомкнутой системы:

САУ ГТД как объект регулирования: Линеаризуем функции Цель: вывести уравнение движения ГТД и

САУ ГТД как объект регулирования: Используем аналитический метод линеаризации: Дадим малые приращения n и Gт - значения моментов на установившемся режиме

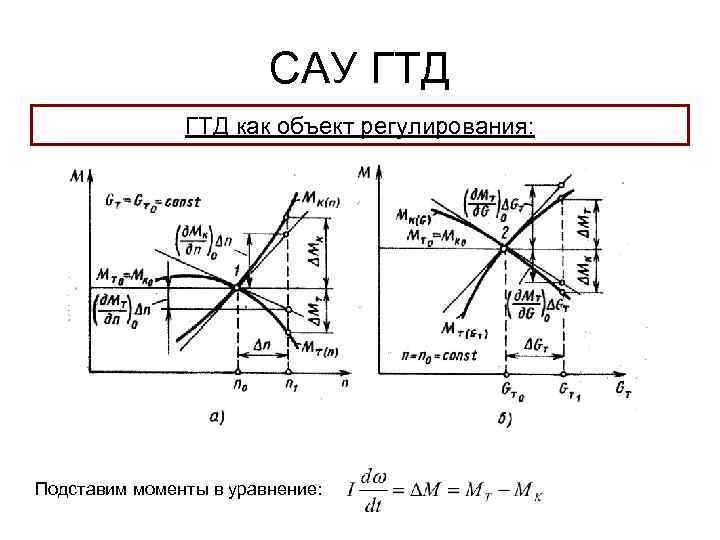САУ ГТД как объект регулирования: Подставим моменты в уравнение:

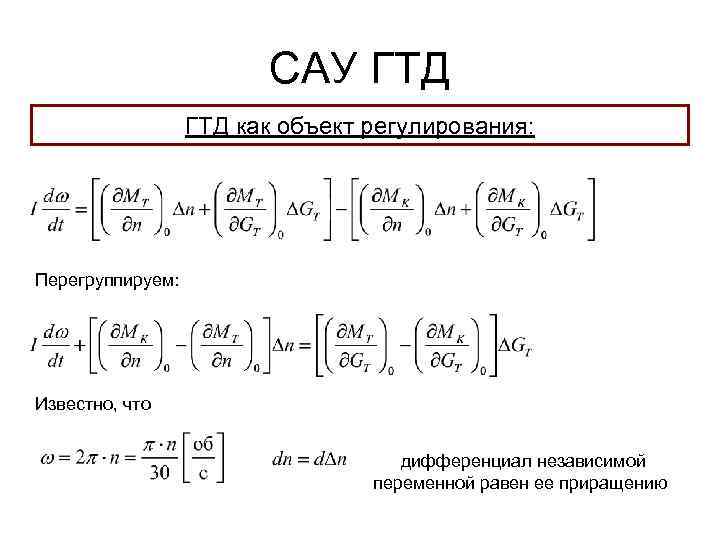САУ ГТД как объект регулирования: Перегруппируем: Известно, что дифференциал независимой переменной равен ее приращению

САУ ГТД как объект регулирования: Получили линейное дифференциальное уравнение с постоянными коэффициентами Для упрощения исследований широкое распространение получили относительные величины воздействий, представляющие собой отношение абсолютных значений воздействий или их отклонений к некоторым базисным значениям

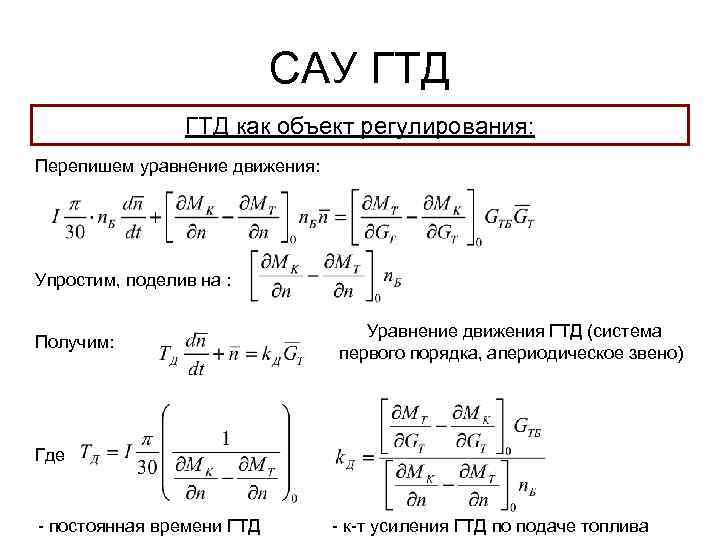САУ ГТД как объект регулирования: Перепишем уравнение движения: Упростим, поделив на : Получим: Уравнение движения ГТД (система первого порядка, апериодическое звено) Где - постоянная времени ГТД - к-т усиления ГТД по подаче топлива

САУ ГТД Анализ уравнения движения ГТД как объект регулирования является инерционным апериодическим звеном Решение диф. уравнения представляет экспоненту: При единичном входном воздействии:

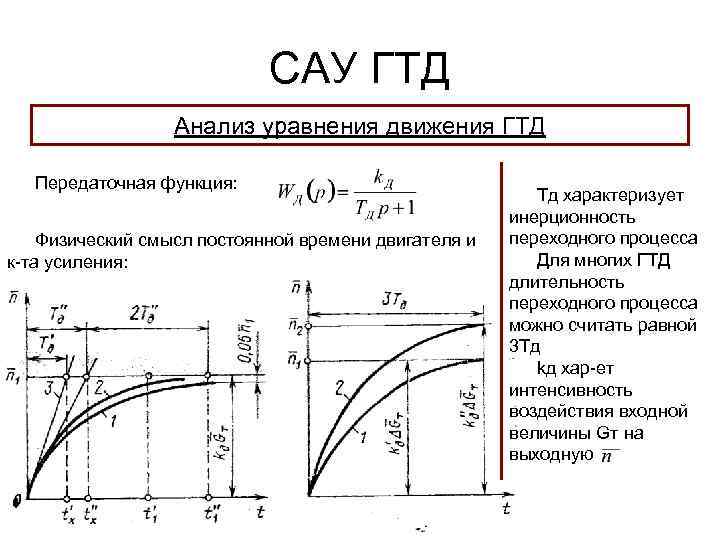САУ ГТД Анализ уравнения движения ГТД Передаточная функция: Физический смысл постоянной времени двигателя и к-та усиления: Тд характеризует инерционность переходного процесса Для многих ГТД длительность переходного процесса можно считать равной 3 Тд kд хар-ет интенсивность воздействия входной величины Gт на выходную

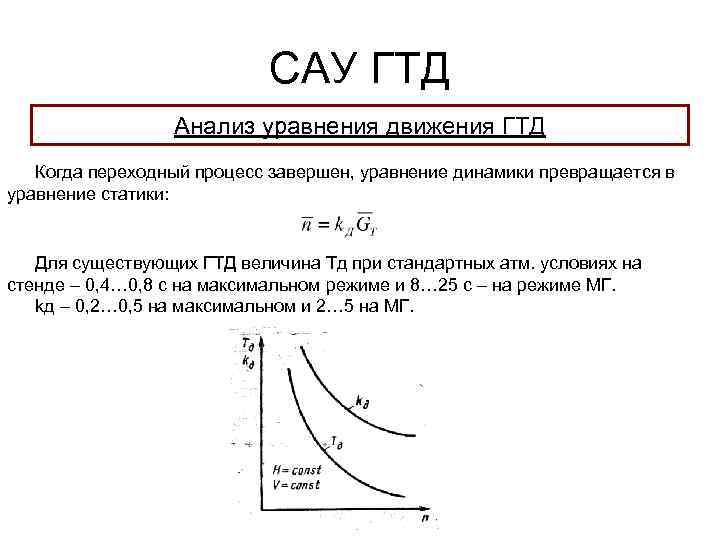САУ ГТД Анализ уравнения движения ГТД Когда переходный процесс завершен, уравнение динамики превращается в уравнение статики: Для существующих ГТД величина Тд при стандартных атм. условиях на стенде – 0, 4… 0, 8 с на максимальном режиме и 8… 25 с – на режиме МГ. kд – 0, 2… 0, 5 на максимальном и 2… 5 на МГ.

САУ ГТД Системы ГТД Конструкция и состав систем ГТД определяются назначением двигателя. Рассмотрим основные системы двигателя: 1. Пусковая система. Включается первой после нажатия кнопки «Запуск» . Управляет стартером. 2. Система автоматического управления. – В процессе запуска управляет механизацией двигателя и ограничивает предельно допустимые параметры ГВТ. – На заданной частоте вращения отключает стартер и зажигание и переводит ГТД на режим МГ. – Сигнал САУ получает от РУД и после назначения режима двигателя поддерживает его за счет подачи топлива по определенному закону и механизации двигателя. Кроме того САУ защищает двигатель от превышения предельных параметров ГВТ и частот вращения роторов.

САУ ГТД Системы ГТД 3. Топливная регулирования. система. Подает топливо согласно программе 4. Система зажигания. Воспламеняет топливо. 5. Бортовая система контроля и диагностики. Получает и передает информацию о параметрах двигателя от датчиков и сигнализаторов в бортовую систему диагностики самолета (в кабину экипажа). Записывает информацию в ЗБН (защищенный от механических воздействий бортовой наакопитель, «черный ящик» ) 6. Система смазки и суфлирования. Подает масло на охлаждение подшипников валов роторов, агрегатов и коробки приводов, а также осуществляет суфлирование с атмосферой масляных полостей. При охлаждении подшипников роторов, получает сигнал от фильтр-сигнализатора стружки в масле. Горячее масло охлаждается в теплообменнике. 7. Дренажная система. Собирает и утилизирует утечки топлива, масла и гидрожидкостей из уплотнений приводных валов агрегатов и слитых из форсунок КС. Собирает и удаляет воду и топливо из ГВТ.

САУ ГТД Системы ГТД 3. Гидросистема. Обеспечивает подачу жидкости высокого давления в гидросистемы самолета, реверсивного устройства и сопла. 4. Воздушная система. Выполняет отбор и подачу воздуха от компрессора на нужды самолета, а также двигателя и его систем (охлаждение, обогрев, наддув и т. д. ). 5. Система пожаротушения. В случае получения сигнала о повышенной температуре в подкапотном пространстве передается сигнал и начинается подача огнегасящих составов. Рассмотрим по отдельности некоторые из приведенных систем:

САУ ГТД Назначение САУ ГТД предназначена для: 1. Управление запуском и выключением двигателя 2. Управление режимом работы 3. Обеспечение устойчивой работы компрессора на переходных и установившихся режимах 4. Предотвращение превышения предельно допустимых параметров ГТД 5. Управление запуском ФК, если есть 6. Обеспечение информационного обмена с системами самолета 7. Управление двигателем по командам из самолетной системы управления 8. Обеспечение контроля исправности элементов САУ 9. Диагностики и оперативного контроля состояния двигателя 10. Выдача информации о состоянии двигателя

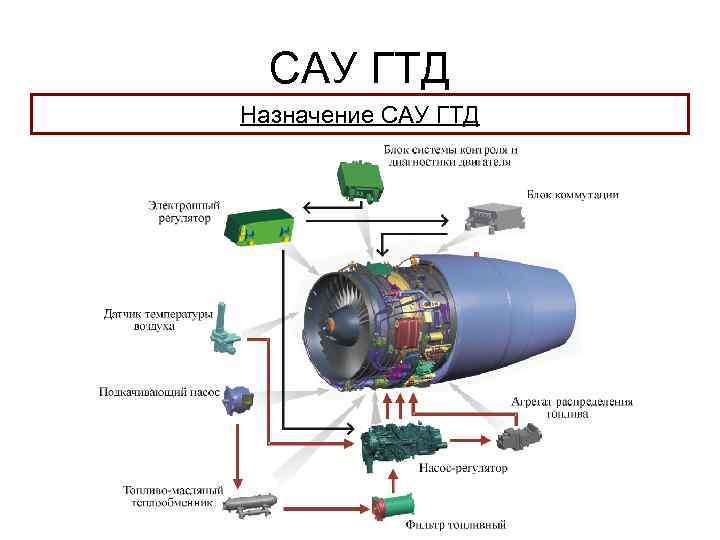САУ ГТД Назначение САУ ГТД

САУ ГТД Состав САУ ГТД В состав САУ ГТД входят следующие агрегаты и датчики: 1. Основной регулятор 2. Датчики электронной части 3. Блок коммутации 4. Автономный генератор 5. Резервный регулятор 6. Агрегат управления механизацией двигателя 7. Агрегат защиты от достижения предельных параметров двигателя 8. Датчики резервного регулятора 9. Исполнительные механизмы 10. Агрегаты топливной системы + дополнительные агрегаты и датчики в зависимости от назначения и типа двигателя

САУ ГТД Датчики электронной части САУ 1. Частоты вращения ротора КВД 2. Частоты вращения ротора вентилятора 3. Температуры газа за турбиной 4. Температуры газа за ТНД на запуске 5. Температуры РЛ первой ступени ТВД 6. Твх 7. Р*вх 8. Р*квд 9. Углового положения ВНА 10. Углового положения РУД 11. Положения ДИ (дозирующей иглы) в составе НР (насоса регулятора) 12. Расхода топлива в КС 13. Наличия пламени в КС 14. Т топлива 15. Т масла на выходе из опор

САУ ГТД Блок коммутации САУ Предназначен для усиления сигналов управления электроагрегатами пусковой системы и коммутации цепей электроагрегатов по сигналам от РЭД, двигателя или из кабины самолета БК обеспечивает также формирование команд на ручном запуске (в воздухе и на земле), если отказал электронный регулятор

САУ ГТД Резервный регулятор САУ Как правило гидромеханический или гидропневмомеханический Он объединен с качающим узлом, дозатором топлива, исполнительной частью электронной системы, агрегатом резервного управления механизацией двигателя. В этом случае его называют «насос-регулятор» (НР) НР при работе на основной САУ предназначен для: – топливоподачи в КС – надсистемного ограничения частоты вращения ротора КВД и давления воздуха за КВД – подвода топлива высокого давления к гидроцилиндрам систем управления механизацией компрессора и отборами воздуха по сигналам РЭД.

САУ ГТД Агрегат управления механизацией двигателя Как правило гидромеханическое или гидропневмомеханическое устройство Управляет: – НА и ВНА – клапанами перепуска воздуха из подпорных ступеней из компрессора и за компрессором – подачей воздуха на охлаждение корпусов компрессора и турбины, а также на охлаждение лопаток турбины При отказе РЭД агрегат может управлять механизацией по упрощенным программам При работе на основной САУ агрегат содержит преобразующие и усилительные элементы, передающие сигналы в исполнительные механизмы

САУ ГТД Основные характеристики САУ ГТД – программы управления – точность выполнения программ – масса, масса сухая – применяемое топливо – параметры топлива на входе – класс чистоты топлива – параметры электропитания – удельные характеристики – устойчивость к внешним воздействиям – ресурс, надежность – ремонтопригодность – эксплуатационная технологичность – технико-экономические показатели – контроллепригодность Как правило САУ рассматривается совместно с системой топливопитания, поэтому некоторые характеристики относятся и к этой системе.

САУ ГТД Работа на режимах запуска: – запуск двигателя на земле – запуск двигателя в полете с подкруткой и без подкрутки ротора компрессора – встречный запуск – холодная прокрутка – ложный запуск Работа на режимах останова: – подача топлива выключается по команде пилота либо автоматически превышении предельных параметров – агрегаты топливной системы (дозатор топлива или распределитель по коллекторам) имеют устройство выключения подачи топлива в КС. Устройство имеет электромагнитный клапан, управляющийся по электрическому сигналу из кабины пилота.

САУ ГТД Работа на основных режимах: Управление ГТД на статических и переходных режимах выполняется по заданным программам в зависимости от: – положения РУД – сигналов бортовой САУ – внутридвигательных параметров – параметров воздуха на входе в двигатель – сигналов от взаимодействующих и управляемых систем двигателя РЭД принимает сигналы от датчиков, вырабатывает управляющие сигналы, выдает их на преобразователи исполнительных механизмов САУ. Исполнительные механизмы приводят регулирующие органы ГТД.

САУ ГТД Работа противопомпажной и противосрывной систем: Датчики помпажных и срывных явлений фиксируют предпомпажное состояние или начальную стадию развития помпажа и выдают сигнал в блок ППС. Помпаж может быть также зафиксирован штатным датчиком измерения давления в тракте компрессора. При фиксировании помпажа приводится в действие механизация компрессора, уменьшается тепловая нагрузка на элементы ГТД

САУ ГТД Работа на режимах обратной тяги: Обычно существуют 2 режима обратной тяги: – минимальная обратная тяга – максимальная обратная тяга Управление статическими и переходными режимами также как при прямой тяге. Управление механизацией, обдувами и зазорами – по упрощенным программам. Для исключения нерасчетной нагрузки на элементы реверсивного устройства на режиме обратной тяги блокируется увеличение режима сверх установленного для мин. обратной тяги. При переходе с режима максимальной обратной тяги на режим прямой тяги, блокируется перекладка реверсивного устройства до тех пор пока режим двигателя не снизится до МГ.

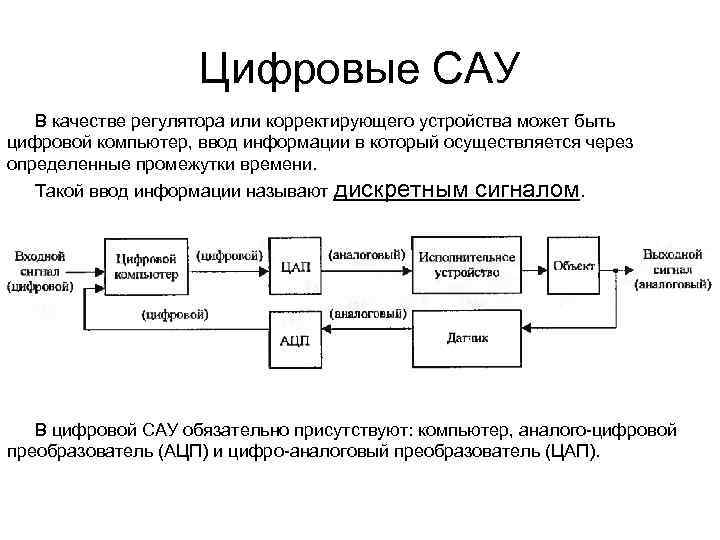Цифровые САУ В качестве регулятора или корректирующего устройства может быть цифровой компьютер, ввод информации в который осуществляется через определенные промежутки времени. Такой ввод информации называют дискретным сигналом. В цифровой САУ обязательно присутствуют: компьютер, аналого-цифровой преобразователь (АЦП) и цифро-аналоговый преобразователь (ЦАП).

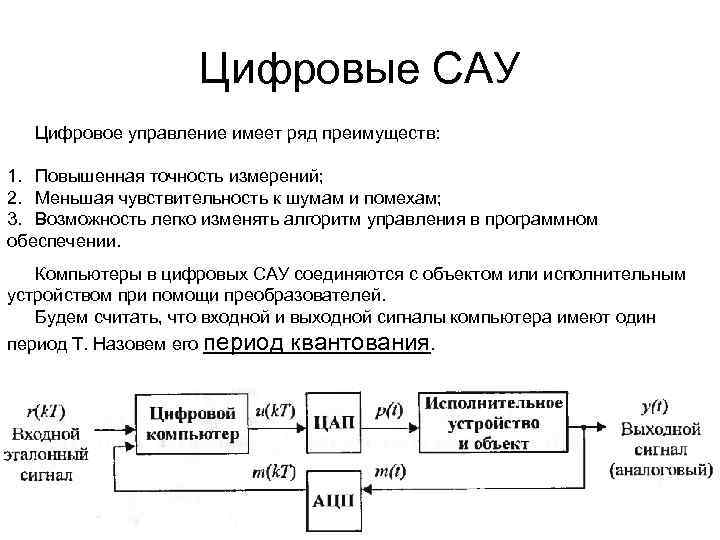Цифровые САУ Цифровое управление имеет ряд преимуществ: 1. Повышенная точность измерений; 2. Меньшая чувствительность к шумам и помехам; 3. Возможность легко изменять алгоритм управления в программном обеспечении. Компьютеры в цифровых САУ соединяются с объектом или исполнительным устройством при помощи преобразователей. Будем считать, что входной и выходной сигналы компьютера имеют один период Т. Назовем его период квантования.

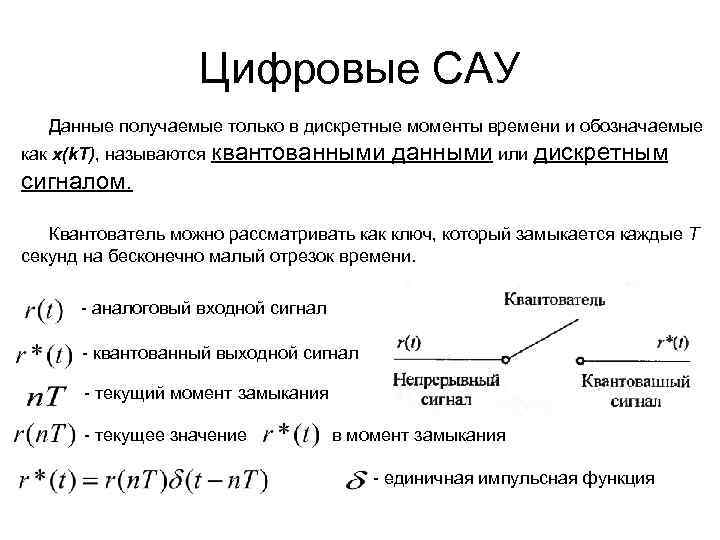Цифровые САУ Данные получаемые только в дискретные моменты времени и обозначаемые как x(k. T), называются квантованными данными или дискретным сигналом. Квантователь можно рассматривать как ключ, который замыкается каждые Т секунд на бесконечно малый отрезок времени. - аналоговый входной сигнал - квантованный выходной сигнал - текущий момент замыкания - текущее значение в момент замыкания - единичная импульсная функция

Цифровые САУ аналоговый входной сигнал квантованный выходной сигнал

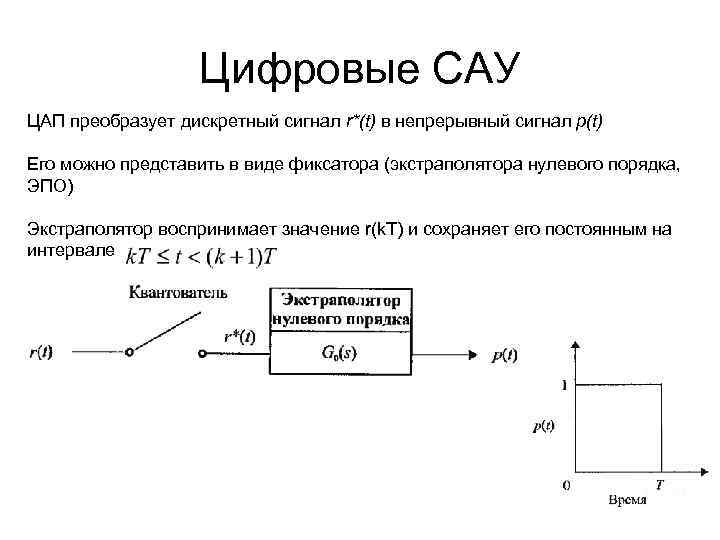Цифровые САУ ЦАП преобразует дискретный сигнал r*(t) в непрерывный сигнал p(t) Его можно представить в виде фиксатора (экстраполятора нулевого порядка, ЭПО) Экстраполятор воспринимает значение r(k. T) и сохраняет его постоянным на интервале

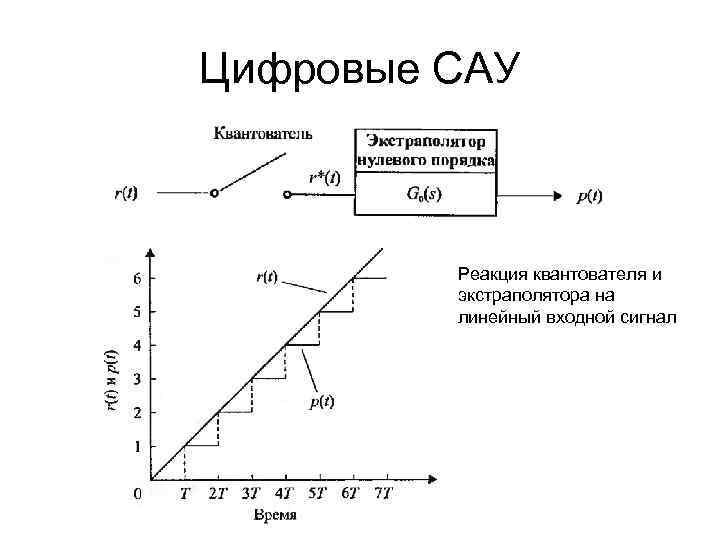Цифровые САУ Реакция квантователя и экстраполятора на линейный входной сигнал

Цифровые САУ обладают ограниченной точностью. Точность в Ц. САУ – это разрешение, с которым определяются отдельные переменные. Точность компьютера ограничена длиной машинного слова. Точность АЦП - числом двоичных разрядов его регистра. Для того, чтобы анализировать Ц. САУ необходимо получить их передаточную функцию. Получение передаточной функции осуществляется по специальным методикам и преобразованиям.

Цифровые САУ Z-преобразование Преобразование Лапласа для непрерывных систем позволяет для линейных дифференциальных уравнений использовать операторную запись Передаточная функция:

Цифровые САУ Z-преобразование Дискретное преобразование Лапласа: замена интеграла конечной суммой замена переменной

Цифровые САУ Z-преобразование Аналог преобразования Лапласа для дискретных систем Позволяет для линейных разностных уравнений использовать операторную запись Передаточная функция

Цифровые САУ Z-преобразование Единичный дискретный импульс 1 t Единичный ступенчатый сигнал 1 t Экспоненциально убывающий сигнал 1 t

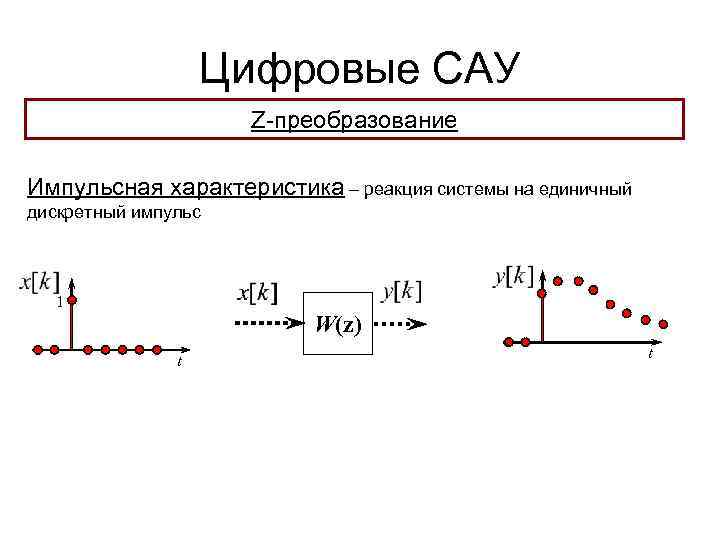Цифровые САУ Z-преобразование Импульсная характеристика – реакция системы на единичный дискретный импульс 1 W(z) t t

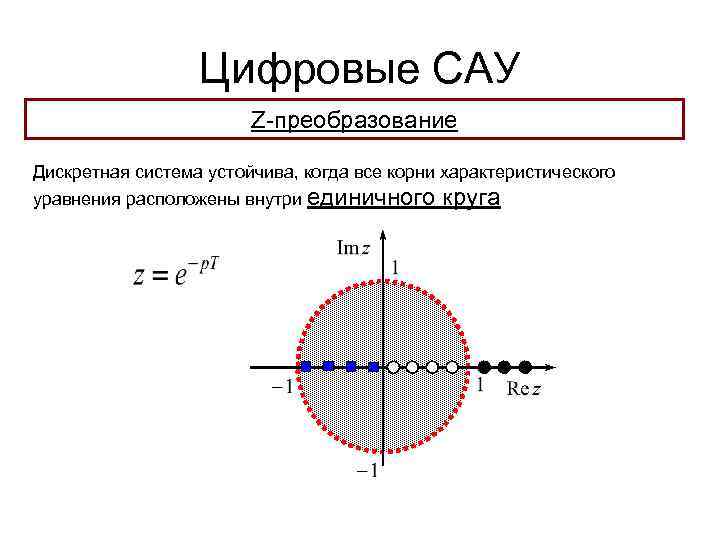Цифровые САУ Z-преобразование Дискретная система устойчива, когда все корни характеристического уравнения расположены внутри единичного круга

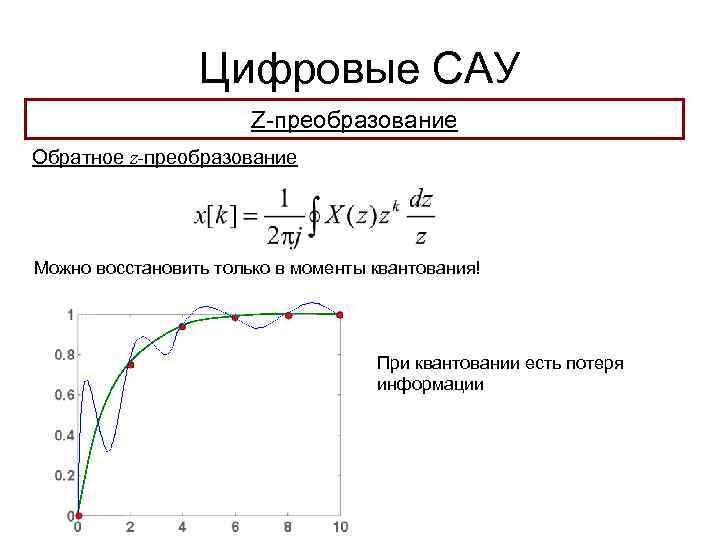Цифровые САУ Z-преобразование Обратное z-преобразование Можно восстановить только в моменты квантования! При квантовании есть потеря информации

Вопросы к экзамену 1. Автоматика и регулирование. Основные термины автоматики. 2. Режимы САУ. Переходный процесс. 3. Классификация САУ. 4. Разомкнутые и замкнутые САУ. 5. Статические характеристики САУ. 6. Динамические характеристики САУ. Виды входных воздействий. 7. Динамическая характеристика системы 1 -го порядка. 8. Передаточная функция. Способ ее получения. 9. Частотные характеристики САУ. 10. Частотная передаточная функция. 11. Динамические звенья САУ. Пропорциональное звено. 12. Интегрирующее звено. 13. Апериодическое звено. 14. Дифференцирующее звено. 15. Колебательное звено. 16. Типовые соединения звеньев. 17. Составление уравнения движения САУ. 18. Свойства управляемых объектов.

Вопросы к экзамену 19. Устойчивость САР. Устойчивость апериодического звена. 20. Устойчивость интегрирующего и колебательного звеньев. 21. Критерий устойчивости Рауса-Гурвица. 22. Критерий устойчивости Михайлова. 23. Критерий устойчивости Найквиста. 24. Показатели качества САР. 25. Диаграммы переходных процессов. 26. Степень устойчивости и степень колебательности. Запасы основных показателей системы. 27. Методы уменьшения статической ошибки САР. 28. Коррекция динамических свойств САР. 29. Жесткие и гибкие обратные связи. 30. Понятие о нелинейных САУ. 31. Графический и аналитический методы линеаризации 32. Метод фазовой плоскости 33. Особые точки фазовой плоскости. Автоколебания. 34. Гармоническая линеаризация. 35. Уравнение движения ГТД. Передаточная функция. 36. Системы ГТД.

Вопросы к экзамену 37. Назначение и состав САУ ГТД. 38. Основные характеристики и работа САУ ГТД на основных режимах. 39. Понятие о цифровых САУ. 40. Квантователь и экстраполятор. 41. Z-преобразование. Передаточная функция. 42. Устойчивость цифровых САУ. Обратное Z-преобразование.

Литература 1. Бесекерский В. А. , Попов Е. П. Теория систем математического регулирования. –М. ; Наука, 2003. + другие издания Бессекерского. 2. Попов Е. П. Теория линейных систем автоматического регулирования и управления. – М. ; Наука, 1989. 3. Попов Е. П. Теория нелинейных систем автоматического регулирования и управления. – М. ; Наука, 1988. 4. Дорф Р. , Бишоп Р. Современные системы управления. – М. ; Лаборатория базовых знаний, 2002 5. Арховский В. Ф. , Серегин Ю. Н. Основы автоматического регулирования. – М. ; «Машиностроение» , 1974.

Порядок проведения экзамена К экзамену по данной дисциплине допускаются студенты, имеющие допуски к сессии от деканата и не имеющие задолженностей по всем проводившимся в течение семестра лабораторным и контрольным работам по данному предмету. Экзамен по дисциплине «Автоматика и регулирование авиационных двигателей и энергетических установок» проводится в устной форме. Каждый экзаменационный билет включает в себя два теоретических вопроса. При формировании оценки каждый из вопросов вносит одинаковый вклад – по 50%. При этом каждый из экзаменующихся в процессе подготовки ответов на вопросы экзаменационного билета должны изложить необходимый материал на выданной преподавателем бумаге. Этот материал облегчает общение преподавателя со студентом в процессе экзамена и ускоряет его проведение. Как правило, в процессе экзамена студенту могут быть заданы дополнительные вопросы по излагаемому материалу из других разделов курса. Это позволяет более полно оценить знания студента, а также, в случае сомнения преподавателя по оценке, подтвердить ее правильность.