24c7d69d33759583d0d15cb9d610943c.ppt
- Количество слайдов: 99

Automatic Verification of Data-Centric Web Services Victor Vianu U. C. San Diego

Web service: service hosted on the Web • Should be accessible by humans or programs: need for standard interface • Should be possible to discover automatically: need for uniform description of functionality • Should be possible to create complex services using simpler ones: Web service composition and synthesis

This talk: automatic verification of Web services • Finite-state abstractions • Beyond finite-state: workflow+data The WAVE verifier
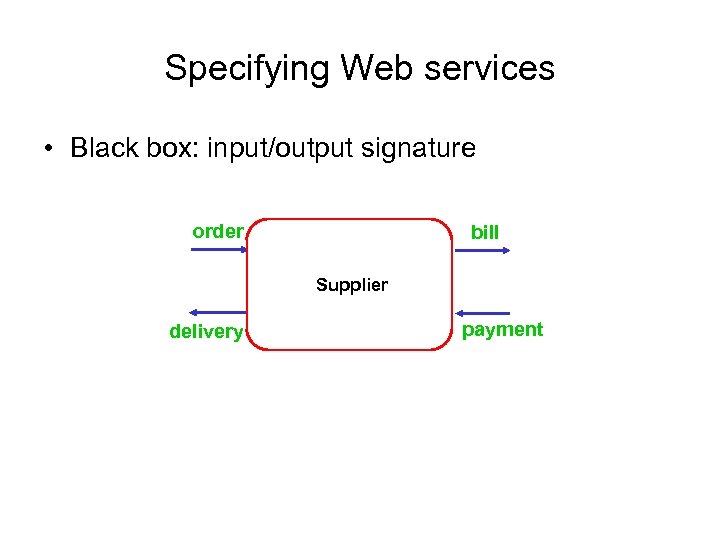
Specifying Web services • Black box: input/output signature order bill Supplier delivery payment
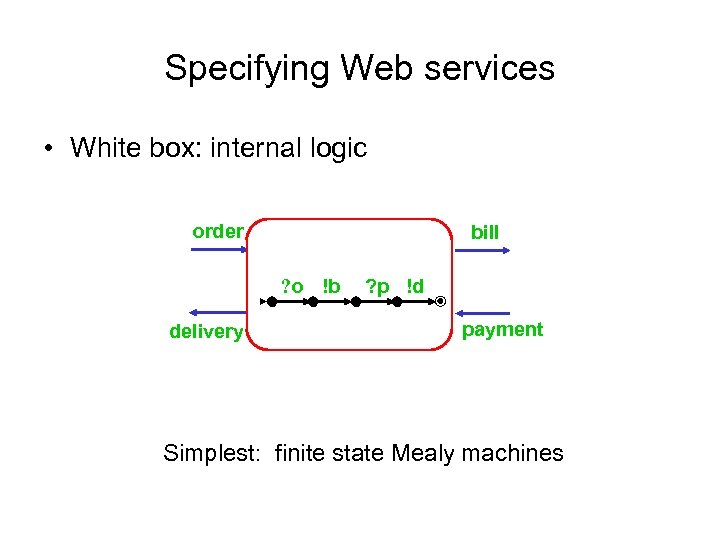
Specifying Web services • White box: internal logic order bill ? o !b delivery ? p !d payment Simplest: finite state Mealy machines
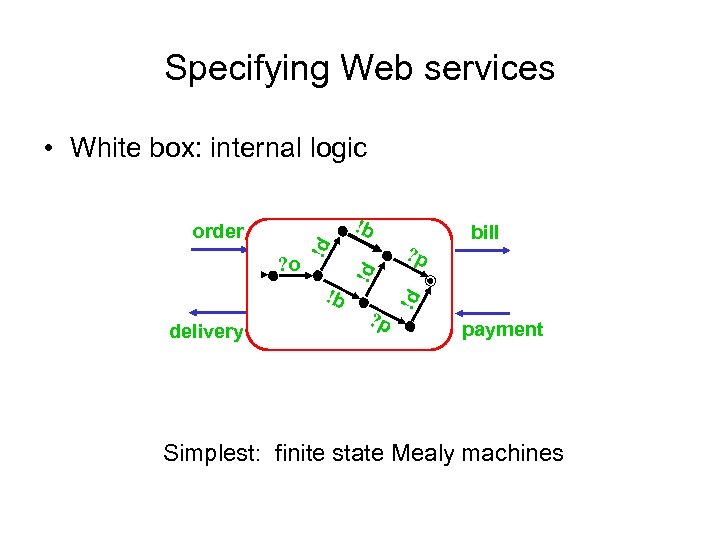
Specifying Web services • White box: internal logic !b delivery ? p bill !d !b !d ? o !d order payment Simplest: finite state Mealy machines
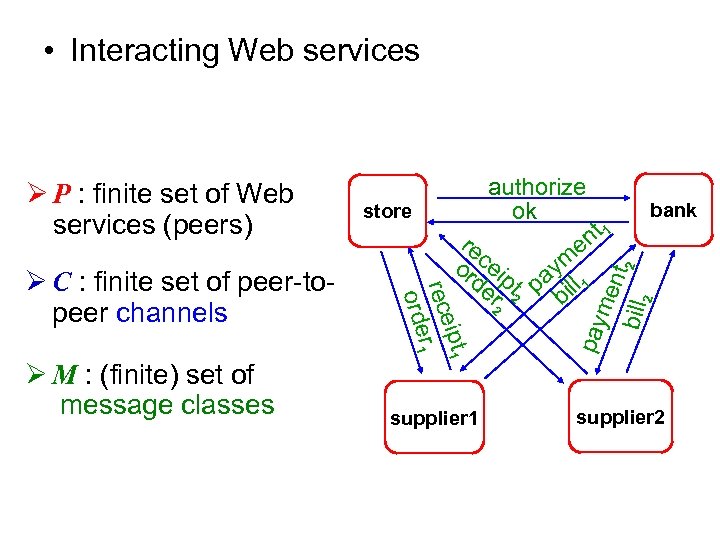
• Interacting Web services Ø M : (finite) set of message classes supplier 1 bank me nt bill 2 2 ipt 1 rece r 1 orde Ø C : finite set of peer-topeer channels store authorize ok nt 1 re e ce m or i pt pay ll 1 de r 2 2 bi pay Ø P : finite set of Web services (peers) supplier 2
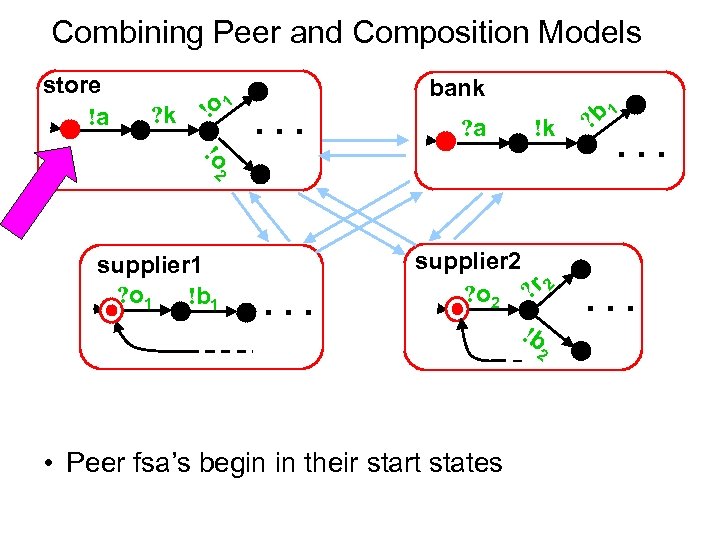
Combining Peer and Composition Models store !a ? k !o 1 bank . . . ? a !k !o 2 supplier 1 ? o 1 !b 1 . . . supplier 2 ? o 2 ? r 2 !b 2 • Peer fsa’s begin in their start states 1 ? b . . .
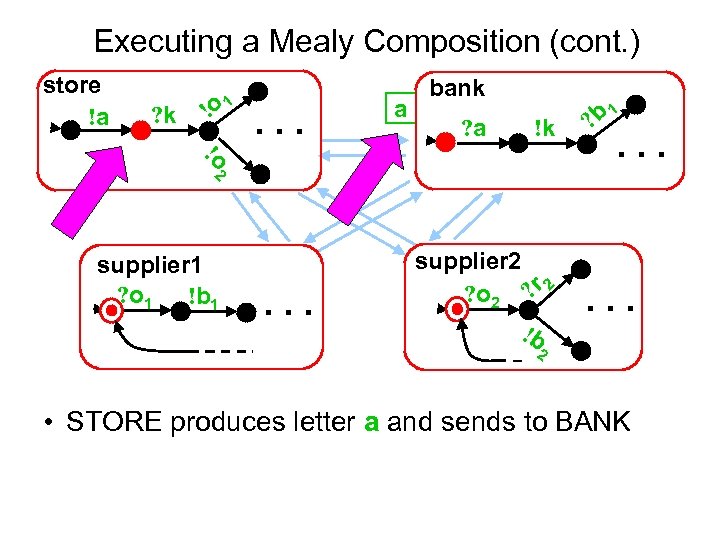
Executing a Mealy Composition (cont. ) store !a ? k !o 1 . . . a bank ? a !k !o 2 supplier 1 ? o 1 !b 1 . . . supplier 2 ? o 2 ? r 2 !b 1 ? b . . . 2 • STORE produces letter a and sends to BANK
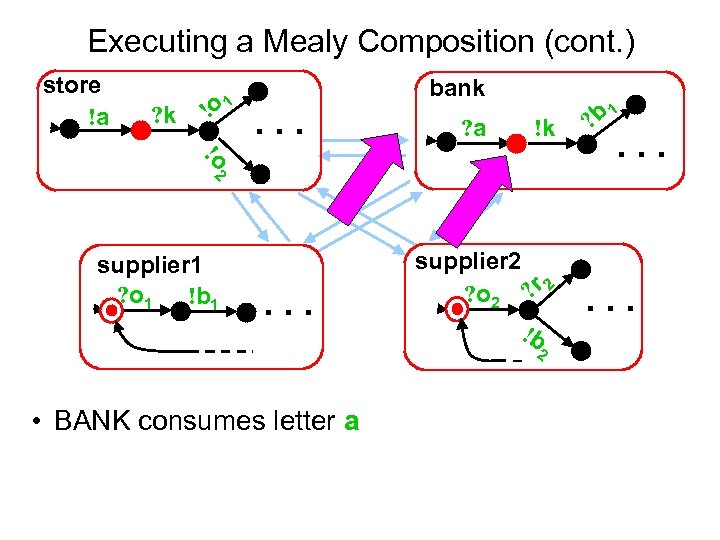
Executing a Mealy Composition (cont. ) store !a ? k !o 1 bank . . . ? a !k !o 2 supplier 1 ? o 1 !b 1 . . . supplier 2 ? o 2 ? r 2 !b 2 • BANK consumes letter a 1 ? b . . .
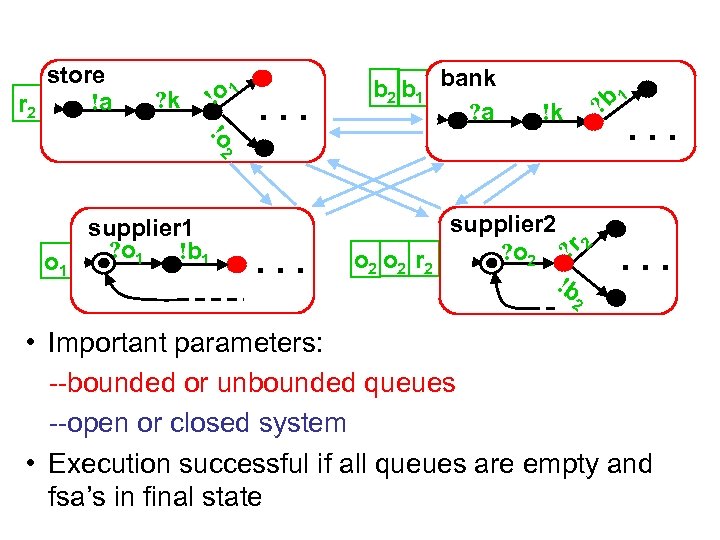
store !a r 2 ! ? k o 1 . . . b 2 b 1 bank ? a 1 ? b !k !o 2 . . . o 1 supplier 1 ? o 1 !b 1 . . . o 2 r 2 supplier 2 ? o 2 ? r 2 !b . . . 2 • Important parameters: --bounded or unbounded queues --open or closed system • Execution successful if all queues are empty and fsa’s in final state
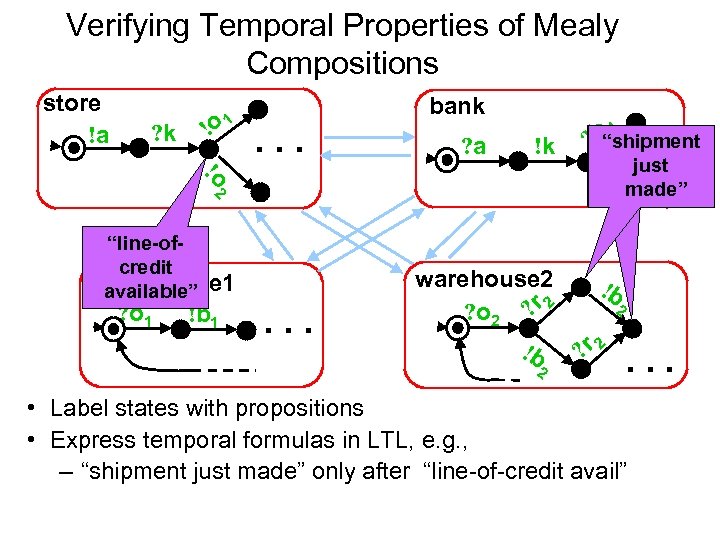
Verifying Temporal Properties of Mealy Compositions store !a ? k ! o 1 bank . . . ? a !k 1 ? b “shipment !o 2 . just. . “line-ofcredit warehouse 1 available” ? o 1 !b 1 made” . . . warehouse 2 ? o 2 ? r 2 !b 2 ? r 2 . . . • Label states with propositions • Express temporal formulas in LTL, e. g. , – “shipment just made” only after “line-of-credit avail”
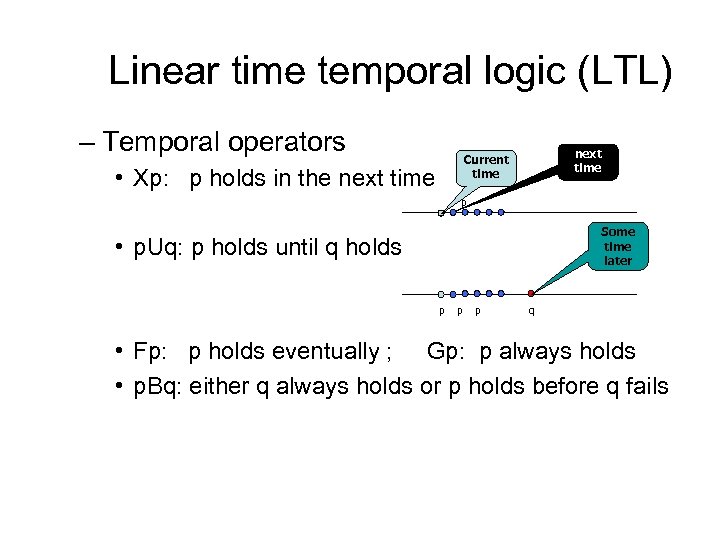
Linear time temporal logic (LTL) – Temporal operators next time Current time • Xp: p holds in the next time p Some time later • p. Uq: p holds until q holds p p p q • Fp: p holds eventually ; Gp: p always holds • p. Bq: either q always holds or p holds before q fails
![Results on Temporal Verification • Long history, see [Clarke et. al. ’ 00] • Results on Temporal Verification • Long history, see [Clarke et. al. ’ 00] •](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-14.jpg)
Results on Temporal Verification • Long history, see [Clarke et. al. ’ 00] • E. g. : one fsa and propositional LTL – PSPACE in size of formula + fsa – linear time in size of fsa • Mealy compositions – Bounded queues • Composition can be simulated as Mealy machine • Verification is decidable • Standard techniques to reduce cost – Unbounded queues • In general, undecidable [Brand & Zafiropulo 83]
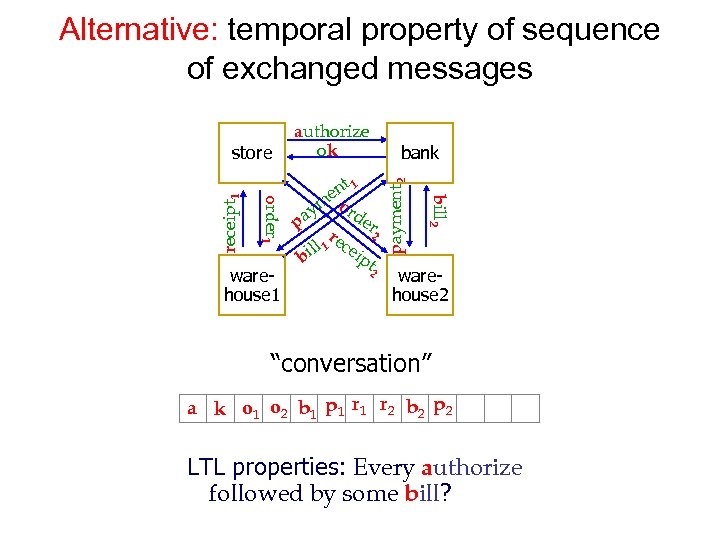
Alternative: temporal property of sequence of exchanged messages warehouse 1 payment 2 nt 1 eo m ay rder p 2 r l 1 ecei l pt bi 2 bank bill 2 order 1 receipt 1 store authorize ok warehouse 2 “conversation” a k o 1 o 2 b 1 p 1 r 2 b 2 p 2 LTL properties: Every authorize followed by some bill?

Conversation languages • Conversation: sequence of exchanged messages • Conversation language: set of all conversations between Mealy peers • Bounded queues: regular language
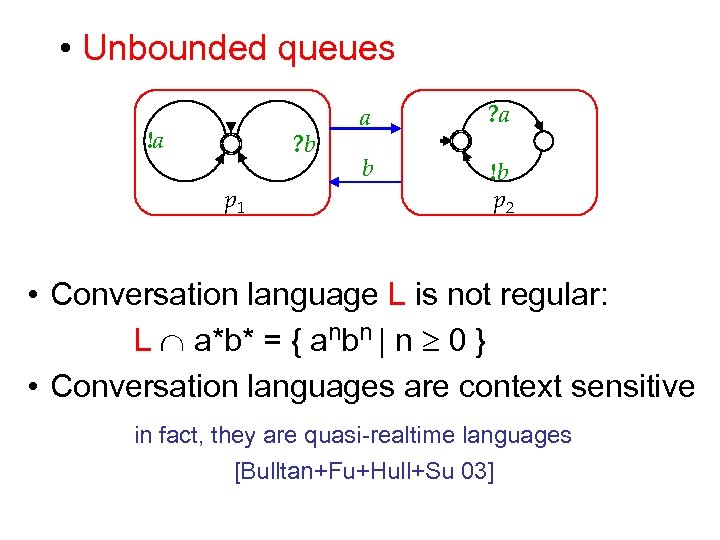
• Unbounded queues !a ? b p 1 a ? a b !b p 2 • Conversation language L is not regular: L a*b* = { anbn | n 0 } • Conversation languages are context sensitive in fact, they are quasi-realtime languages [Bulltan+Fu+Hull+Su 03]

Synthesis of compositions • Given a set of peers and communication channels with message names, and a constraint Φ on the conversation language, find Mealy automata for peers so that the constraint is satisfied.

Bounded queues • Closed systems: PSPACE for LTL PTIME for ω-regular sets given by an automaton • Open systems: “game” against environment synthesis = finding winning strategy undecidable for arbitrary topology hierarchical topology: decidable [Kupferman + Vardi 01] but non-elementary even in linear case [Pnueli+Rosner] [

Unbounded queues • Open systems: undecidable • Closed systems: open
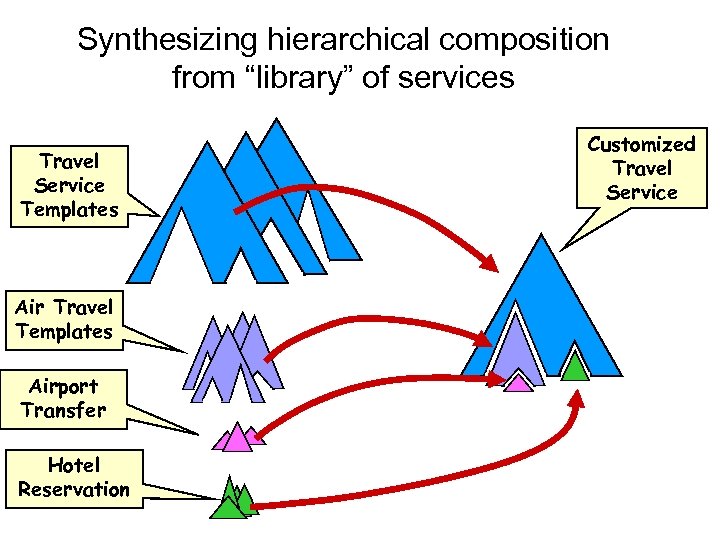
Synthesizing hierarchical composition from “library” of services Travel Service Templates Air Travel Templates Airport Transfer Hotel Reservation Customized Travel Service

Beyond fsa: workflow+data
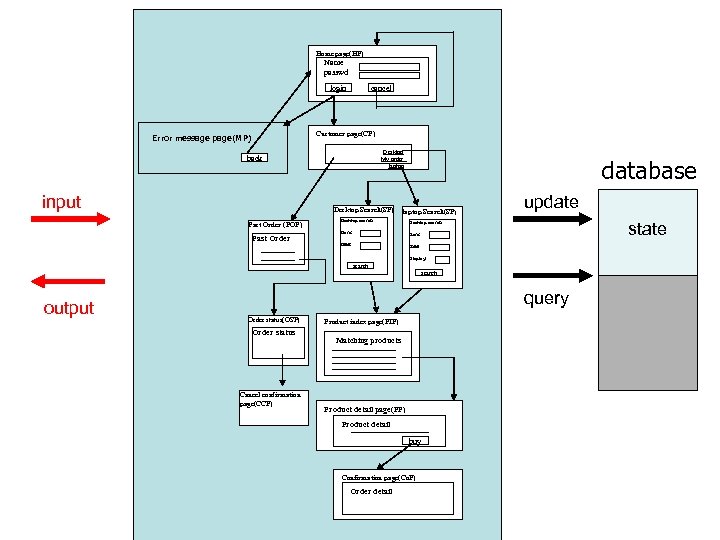
Home page(HP) Name Home page(HP) passwd Name passwd login Error message page(MP) back input cancel Customer page(CP) Desktop My order Desktop laptop My order laptop Desktop Search(SP) Past Order (POP) Past Order database laptop Search(SP) Desktop search Desktop Search(SP) laptop search Desktop search Ram: Hdd: Display: search Order status(OSP) Order status Orderstatus(OSP) Order status Cancel confirmation page(CCP) Product index page(PIP) Matching products Product detail page(PP) Product detail buy Confirmation page(Co. P) Order detail state Display: search output update query

Motivation • Interactive, data-driven Web applications: powered by an underlying database and interacting with external users according to explicit or implicit workflow • Complexity of workflow leads to bugs: see the public database of Web site bugs (Orbitz bug) • Static analysis required to increase confidence in correctness and robustness of applications • Problem: Data-driven Web applications are infinite-state systems !

The WAVE Verifier • WAVE = Web Application VErifier • Practical, sound and complete automatic verification for data-driven applications • Novel coupling of model checking and database optimization techniques.
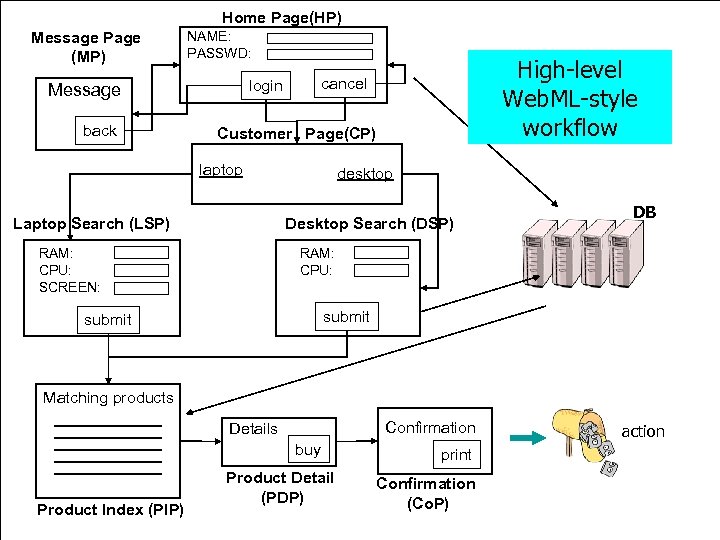
Home Page(HP) Message Page (MP) NAME: PASSWD: Message back High-level Web. ML-style state update workflow cancel login Customer Page(CP) laptop Laptop Search (LSP) desktop Desktop Search (DSP) RAM: CPU: SCREEN: DB RAM: CPU: submit Matching products Confirmation Details buy Product Index (PIP) Product Detail (PDP) print Confirmation (Co. P) action

Modeling Web Applications A Web application is described by • the set of – – database relations D (fixed during a session) state relations S (updateable) input relations I (hold user’s input choice) action relations A • and a set of web page schemas (templates) – their contents are determined at run-time, as function of D, S, I

Webpage Schema • Input options (user may pick at most one of them) – Query(DB, State, Previous input) • Actions and Transitions (triggered by user input) – Actions: Query(DB, State, Input, Prev. input) – Next Webpage: Query(DB, State, Input, Prev. Input ) • State updates (triggered by user input) – insertions/deletions : Query(DB, State, Input, Prev. Input) “Query”: First Order Logic formula (core SQL)

Details on Modeling the Input • input options as provided by menus, pull-down lists, buttons, HTTP links: user must choose one • input constants model text input boxes: name, password, etc. • input I at previous step: prev-I can be viewed as special state
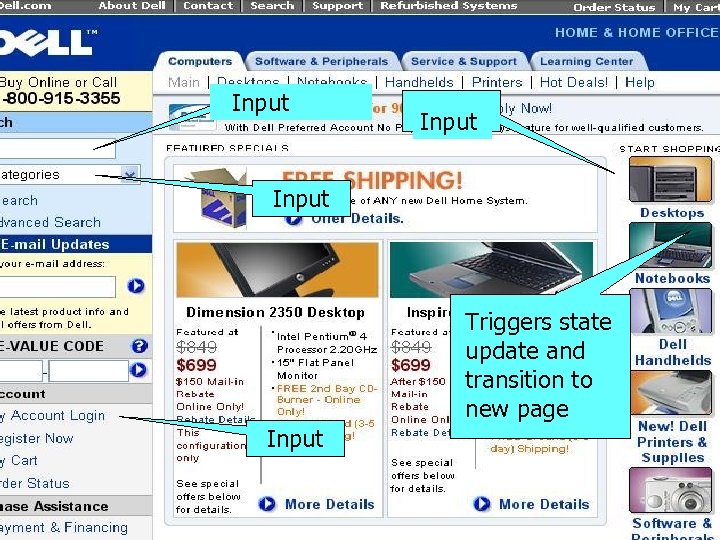
Input Triggers state update and transition to new page Input
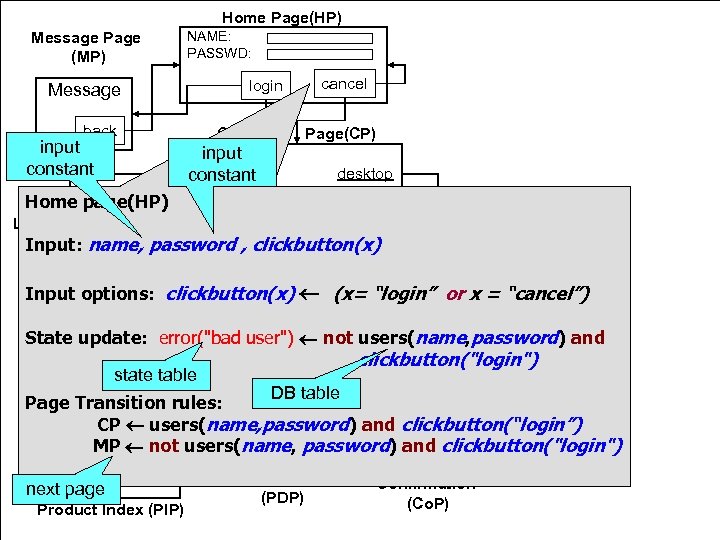
Home Page(HP) Message Page (MP) NAME: PASSWD: login Message back input constant cancel Customer Page(CP) input laptop constant desktop Home page(HP) Laptop Search (LSP) Desktop Search (DSP) Input: name, password , clickbutton(x) RAM: CPU: SCREEN: CPU: Input options: clickbutton(x) (x= “login” or x = “cancel”) submit State update: error("bad user") not users(name, password) and clickbutton("login") state table DB table Matching products Page Transition rules: CP users(name, password) and clickbutton(“login”) Confirmation Details MP not users(name, buy password) and print clickbutton("login") next page Product Index (PIP) Product Detail (PDP) Confirmation (Co. P)
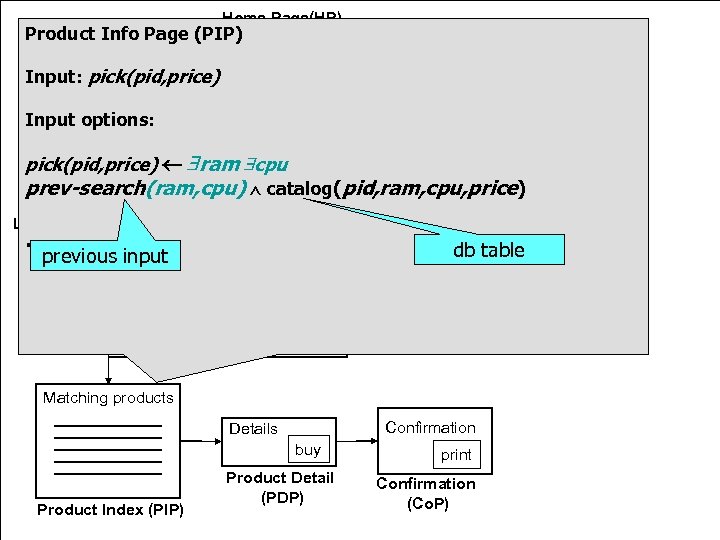
Home Page(HP) Product Info Page (PIP) NAME: Message PASSWD: (MP) Input: pick(pid, price) login Message Input options: back cancel Customer Page(CP) pick(pid, price) ram cpu laptop desktop prev-search(ram, cpu) catalog(pid, ram, cpu, price) Laptop Search (LSP) Desktop Search (DSP) … RAM: previous input RAM: CPU: SCREEN: db table submit Matching products Confirmation Details buy Product Index (PIP) Product Detail (PDP) print Confirmation (Co. P)
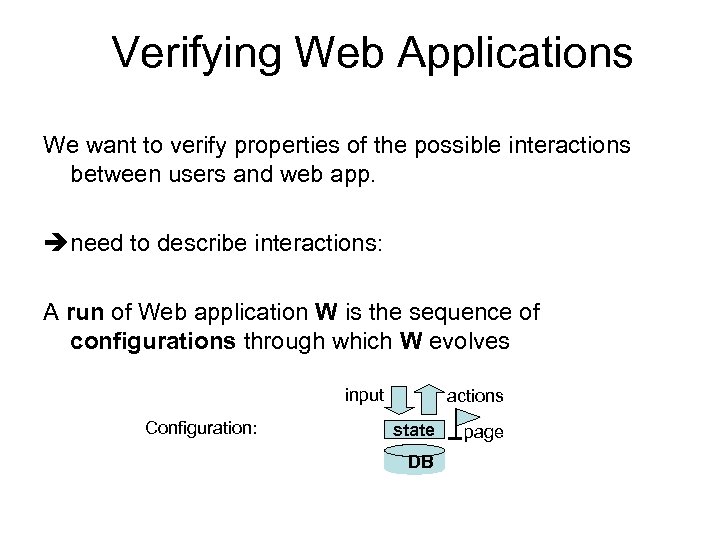
Verifying Web Applications We want to verify properties of the possible interactions between users and web app. need to describe interactions: A run of Web application W is the sequence of configurations through which W evolves input Configuration: actions state DB page

Examples of Desirable Properties • Semantic properties – “no product is delivered before payment in the right amount is received" – “no user cancel an order that has already been shipped” • Basic soundness of specification – “conditions guarding transition to next Web page are mutually exclusive” • Navigational properties – “the shopping cart page is reachable from any page”

Expressing properties in LTL-FO: First-Order logic + linear temporal logic operators • Xp: p holds in the next time step • p. Uq: p holds until q holds • Fp: p will finally hold • Gp: p generally holds (in all steps) • p. Bq: p must hold before q holds More expressive than classical (propositional) LTL
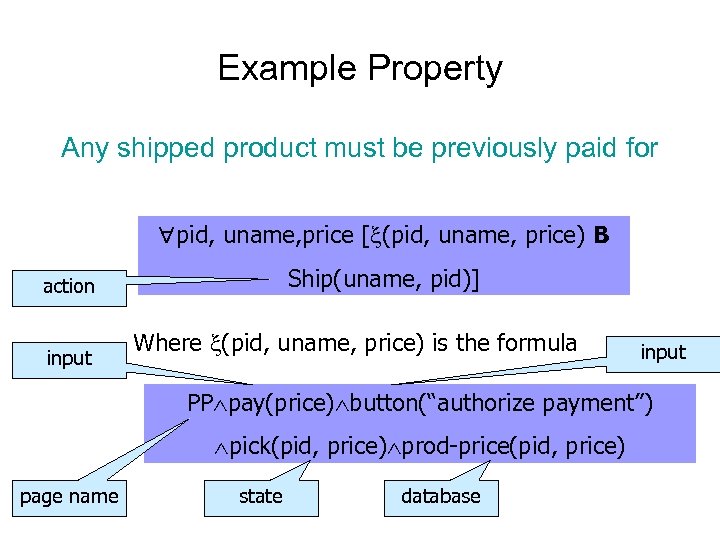
Example Property Any shipped product must be previously paid for pid, uname, price [ (pid, uname, price) B Ship(uname, pid)] action input Where (pid, uname, price) is the formula input PP pay(price) button(“authorize payment”) pick(pid, price) prod-price(pid, price) page name state database

The Verification Problem Given Web application W and LTL-FO property P Decide if every run of W satisfies P. If not, exhibit a counterexample run.
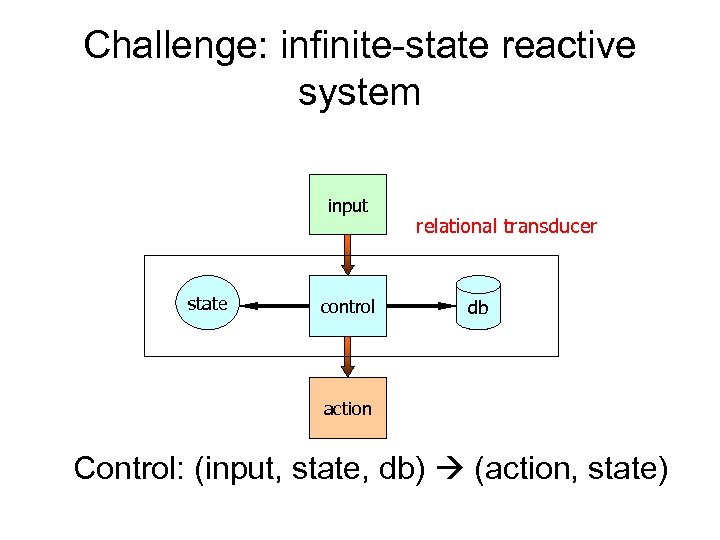
Challenge: infinite-state reactive system input state control relational transducer db action Control: (input, state, db) (action, state)

Verification of Infinite-State Systems • Typical approaches in Software Verification are unsatisfactory: – Model checking: developed for finite-state systems described by propositional states. More expressive specifications first abstracted to propositional ones. Unsatisfactory: can check that some payment occurred before some shipment, but not that it involved the correct amount and product. – Theorem proving: not autonomous. Prover gets stuck during search and asks for guidance from expert user.
![Verification results for LTL-FO [PODS’ 04] • The verification problem is undecidable • Restriction Verification results for LTL-FO [PODS’ 04] • The verification problem is undecidable • Restriction](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-41.jpg)
Verification results for LTL-FO [PODS’ 04] • The verification problem is undecidable • Restriction for decidability: input boundedness – Essentially, input-guarded quantification, i. e. quantified variables must appear in input atoms pick(pid, price) ram cpu prev-search(ram, cpu) catalog(pid, ram, cpu, price)

Input-bounded specs • State, action, and transition rules use FO conditions with “input-bounded” quantification: x ( input( x ) φ( x )) x ( input( x ) φ( x )) state atoms have no quantified variables prev-I can also serve as guard • Input options definitions: *FO (db, prev-input, ground state atoms)

Input-bounded LTL-FO property: FO components are input bounded “An order is rejected in the next step only if it has already been ordered but not paid correctly in the current input” x G [ X reject-order(x) (past-order(x) y (pay(x, y) price(x, y)))]

Verification results: If W and P are input-bounded, checking whether W satisfies P is PSPACE-complete Even modest relaxations of input boundedness restriction lead to undecidability.

Extensions leading to undecidability • Relaxing the requirement that state atoms must be ground in formula defining the input options. Reduction: Does TM halt on input epsilon? • Lifting the input-bounded requirement by allowing state projection. Reduction: Implication for FDs and IDs • Allowing Prev-I to record all previous input to I rather than the most recent one. Reduction: Trakhtenbrot’s Theorem • Extend the FO-LTL formulas with path quantification. Reduction: validity of * *FO formulas

Expressivity of Input-bounded Specs. See demo site http: //www. db. ucsd. edu for modeling of significant parts of the following Web applications: • • Dell-like computer shopping website Expedia Barnes&Noble Grand. Prix motor sport Web site

How to verify To check that W satisfies P, verify that there is no run satisfying P. Model checking approach (finite-state): • Build Buchi automaton A( P) for P • Build automaton S accepting all runs • Check that there is no counterexample run: emptiness of S X A( P)

Our case: infinite-state system Verification: build A( P), then search for counterexample runs accepted by A( P) But: no automaton S for the runs! Challenge in searching for counterexample runs: infinite runs infinitely many underlying databases How to limit the search space?
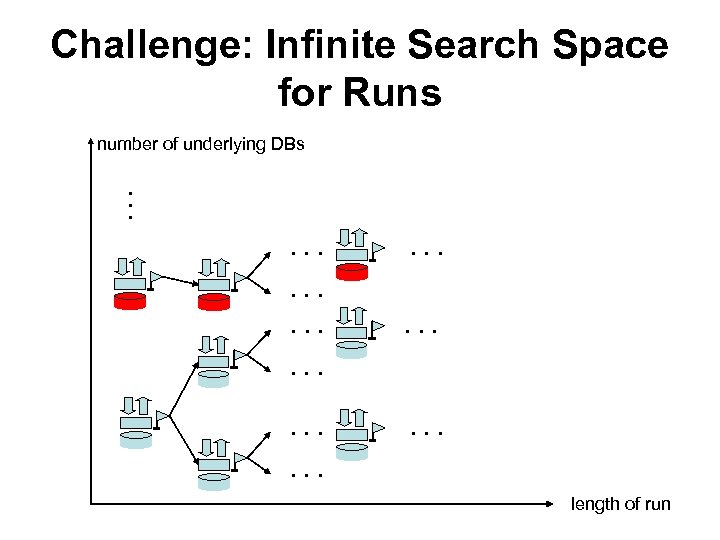
Challenge: Infinite Search Space for Runs number of underlying DBs . . . . length of run
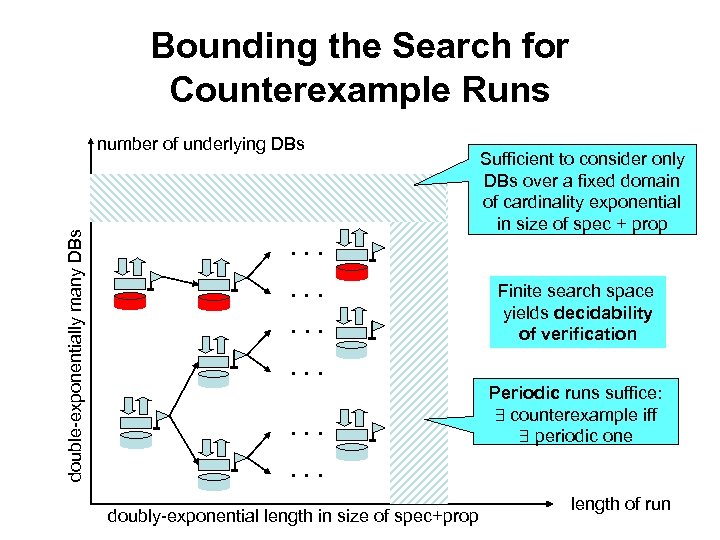
Bounding the Search for Counterexample Runs double-exponentially many DBs number of underlying DBs . . . . Sufficient to consider only DBs over a fixed domain of cardinality exponential in size of spec + prop Finite search space yields decidability of verification . . Periodic runs suffice: counterexample iff periodic one . . . doubly-exponential length in size of spec+prop length of run

Key insight for PSPACE complexity No need to explicitly materialize entire configuration: Instead, at each step construct only those portions of DB, state and actions which can affect property. Call them pseudoconfigurations. Pseudorun: the resulting sequence of pseudoconfigurations. counterexample run iff counterexample pseudorun Pseudoconfigs have size polynomial in size of spec + prop PSPACE verification algorithm
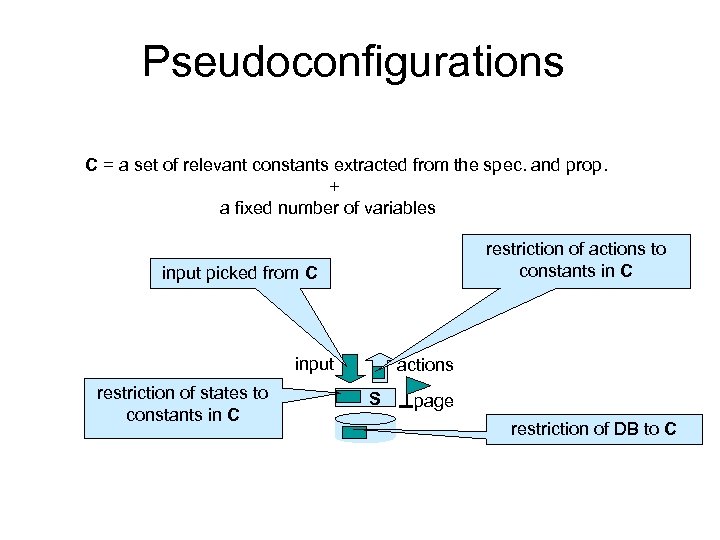
Pseudoconfigurations C = a set of relevant constants extracted from the spec. and prop. + a fixed number of variables restriction of actions to constants in C input picked from C input restriction of states to constants in C actions S page restriction of DB to C

Pseudoruns pseudorun . . . DB DB DB • pseudoconfigs have size polynomial in size of spec + prop • we never construct entire DB, just “slide” poly window over it! PSPACE verification algorithm
![The WAVE Verifier [SIGMOD’ 05] • Essentially implements search for a counterexample pseudorun • The WAVE Verifier [SIGMOD’ 05] • Essentially implements search for a counterexample pseudorun •](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-54.jpg)
The WAVE Verifier [SIGMOD’ 05] • Essentially implements search for a counterexample pseudorun • Many tricks and heuristics to achieve good verification times

Reducing the number of pseudoruns For computer shopping Website: Specification contains 29 constants (“login”, “cancel”, “submit”, “admin”, etc. ). Four DB tables of arity 2, 3, 5 and 7. Yield 2^(29^2 + 29^3 + 29^5 + 29^7) = 2^(17, 270, 412, 688) partial DBs!

Heuristics for Pruning Pseudoruns • Only some combinations of constants are relevant Ex: button values compared to “cancel”, “login”, “submit”, “register”, user names to “admin”, but not conversely! A DB tuple listing a user named “cancel” is irrelevant to pseudorun and should not be constructed in the first place. • In general, Dataflow analysis identifies all constants to which a DB attribute may be compared (directly or indirectly). This limits the relevant combinations of constants when constructing partial DBs. • Spectacular reduction: for the computer shopping website, from 2^(17, 270, 412, 688) partial DBs to 8 !

More Tricks • Internal representation of pseudoconfigs to – Efficiently detect loop in periodic run – Efficiently evaluate queries • Early pruning of pseudoruns as soon as property is violated • See Sigmod 05 paper for more

Experimental Evaluation of WAVE Tool • Online Demo at http: //www. db. ucsd. edu/ • WAVE was evaluated experimentally on 4 Web applications: – Dell-like computer shopping – Part of Expedia, Barnes&Noble, Grand. Prix • We measured verification time for a battery of properties: all within seconds, below one minute. • Here, report only Dell experiment. All others are similar.
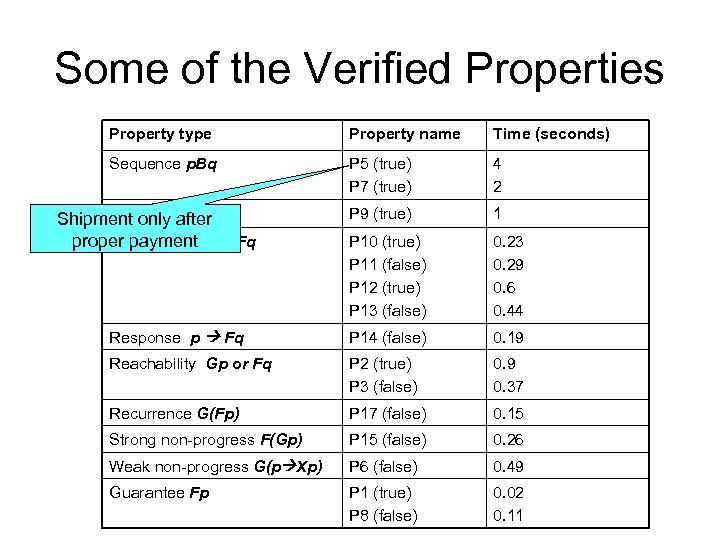
Some of the Verified Properties Property type Property name Time (seconds) Sequence p. Bq P 5 (true) P 7 (true) 4 2 P 9 (true) 1 P 10 (true) P 11 (false) P 12 (true) P 13 (false) 0. 23 0. 29 0. 6 0. 44 Response p Fq P 14 (false) 0. 19 Reachability Gp or Fq P 2 (true) P 3 (false) 0. 9 0. 37 Recurrence G(Fp) P 17 (false) 0. 15 Strong non-progress F(Gp) P 15 (false) 0. 26 Weak non-progress G(p Xp) P 6 (false) 0. 49 Guarantee Fp P 1 (true) P 8 (false) 0. 02 0. 11 Session after Shipment only. Gp Gq proper payment Fq Correlation Fp

Failure of Classical Tools • SPIN model checker Abstraction is unsatisfactory. Alternative trick: Try to use SPIN to verify pseudoruns. The resulting SPIN input is too large to handle. • PVS theorem prover Not guaranteed to find a counterexample. Gets stuck during search, asks for guidance from expert user.
Work in progress: composition of Web services Buyer Login page(BP) Name passwd login cancel Category choice page(CP) My order Desktop laptop Desktop Search(SP) Past Order (POP) Past Order User payment(UPP) laptop Search(SP) Desktop search Ram: Hdd: search Desktop search Ram: Hdd: Display: Credit Verification Payment CC No: Expire date search M submit Order status(OSP) Order status Cancel confirmation page(CCP) Product index page(PIP) Matching products Product detail page(PP) Product detail buy Confirmation page(Co. P) Order detail

Conclusions • Sound and complete verification is feasible for a significant class of database-powered (hence infinitestate) Web services. • The verification times are surprisingly good: incomplete verification of software often takes days, even after abstraction. Our results suggest that • database-powered Web applications may be unusually well suited for automated verification. • Coupling of database and model-checking techniques is extremely effective.

Demo Site http: //www. cs. ucsd. edu/~lsui/project/index. html

Merci !
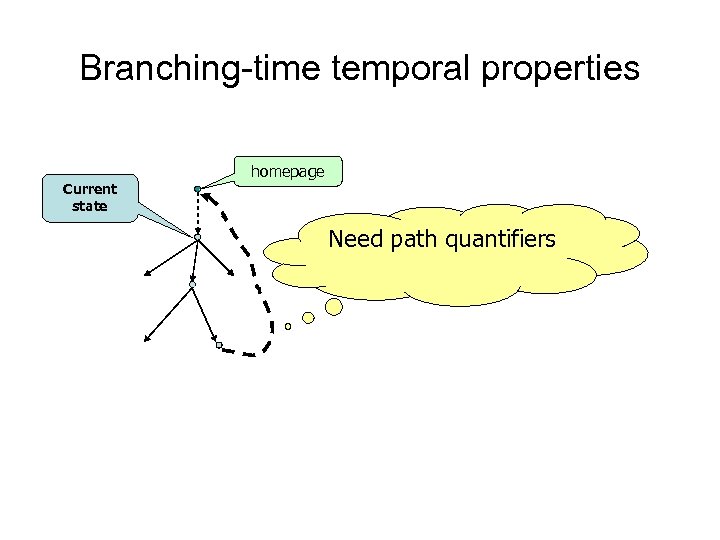
Branching-time temporal properties Current state homepage Need path quantifiers

Branching-time temporal properties • Computation tree logic (CTL*|CTL) Add path quantifiers: • A---”for every path” • E---”there exists a path”
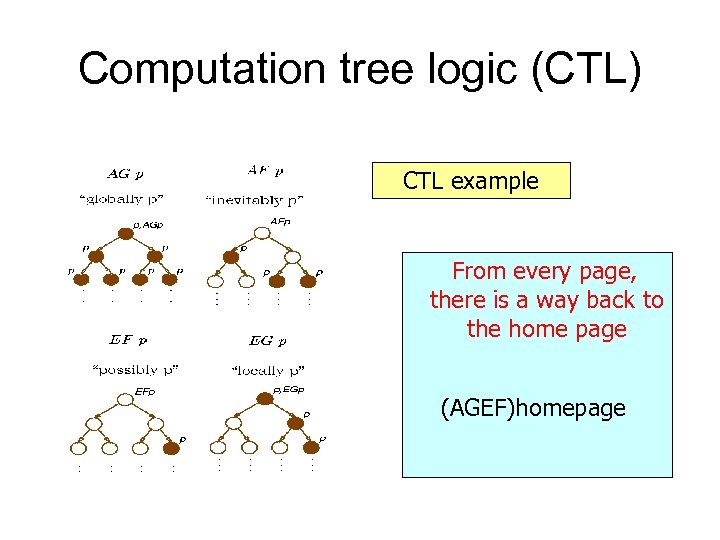
Computation tree logic (CTL) CTL example From every page, there is a way back to the home page (AGEF)homepage

Verification results for CTL(*) • Propositional transducers: --states and outputs are propositional --prev-I atoms are disallowed • CTL* formulas using state, output, and inputs interpreted as propositions

• Verification of CTL(*) formulas for propositional transducers: --CO-NEXPTIME for CTL --EXPSPACE for CTL* Proof idea: (i) show that there is a bound on the databases that need to be considered in order to detect a violation; (ii) for a fixed database, reduce checking violation to model checking for a Kripke structure generated from the database.

Getting down to PSPACE: • Fully propositional transducers: inputs are also propositional Proof technique: highly efficient model-checking technique of Kupferman, Vardi, Wolper using hesitant alternating tree automata (HAA). Reduce to checking emptiness of a one-letter word HAA.

Alternative restriction: capturing “user-driven search” • Propositional states and actions • Inputs are monadic, propagated using prev-I atoms Example: allows conducting a user-driven search going through consecutive stages of refinement

For transducers with “user-driven search”: CTL formulas can be verified in EXPTIME CTL* formulas can be verified in 2 -EXPTIME for fixed out-degree of input choice Proof: reduce to satisfiability of CTL(*) formulas by a Kripke structure

Application: verification for Web services • Basic soundness of specification “no input constant is required before it is supplied” “the next Web page is always uniquely defined” • Semantic properties “no product is delivered before payment of the right amount is received" “no user cancel an order that has already been shipped” • Navigational properties “there is a way to reach the home page from any page”

Next step • Practical tools for verification SPIN ? symbolic model-checking? • Multiple users, sessions. . . • Modeling Web service compositions • Analysis of compsitions • Synthesis of compositions
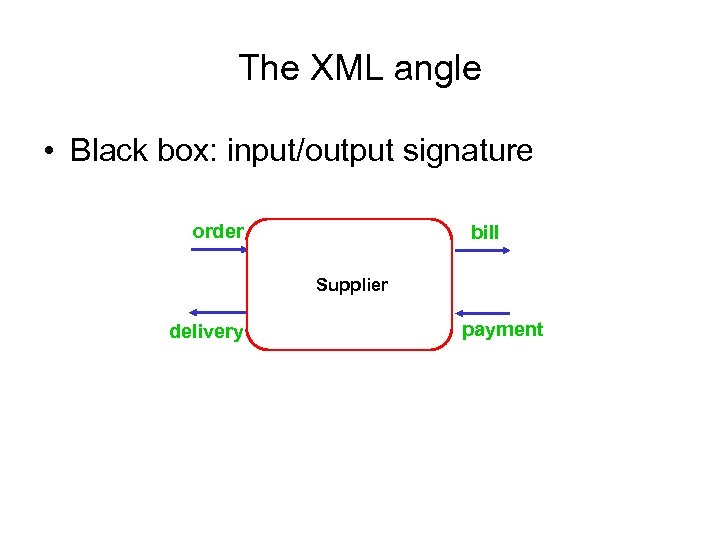
The XML angle • Black box: input/output signature order bill Supplier delivery payment
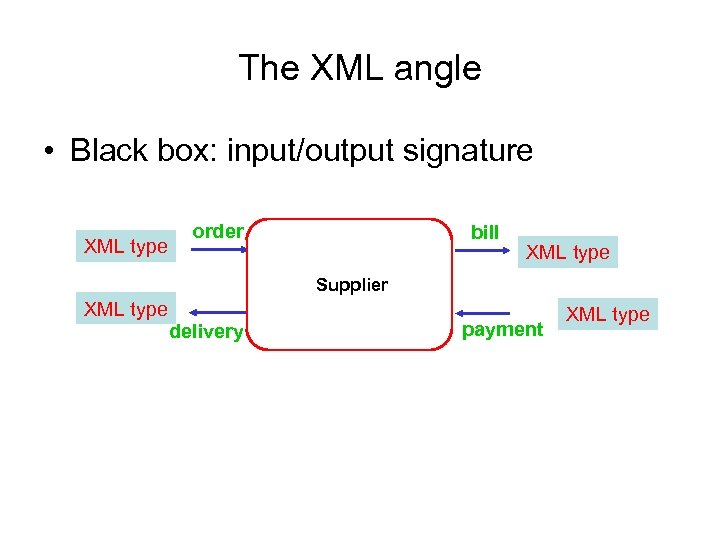
The XML angle • Black box: input/output signature XML type order bill XML type Supplier XML type delivery payment XML type
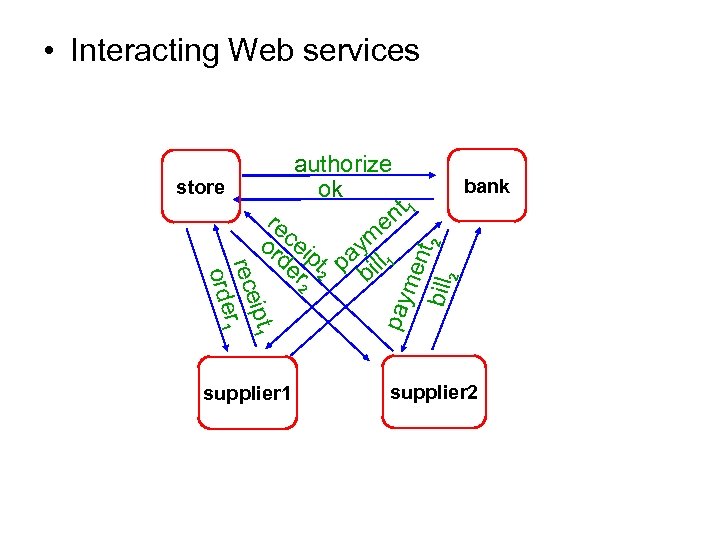
• Interacting Web services me nt bill 2 2 ipt 1 rece r 1 orde supplier 1 bank pay store authorize ok nt 1 re e m or cei de pt pay ll 1 r 2 2 bi supplier 2
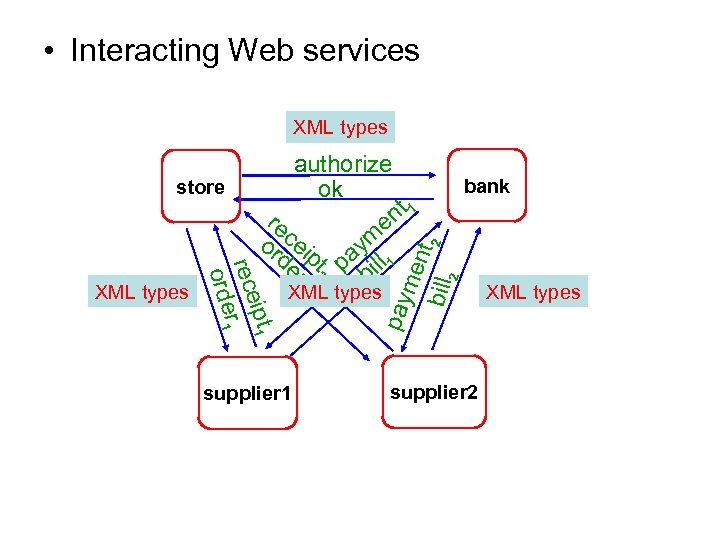
• Interacting Web services XML types supplier 1 me nt bill 2 2 ipt 1 rece r 1 orde XML types bank pay store authorize ok nt 1 re e m or cei de pt pay ll 1 r 2 2 bi supplier 2 XML types
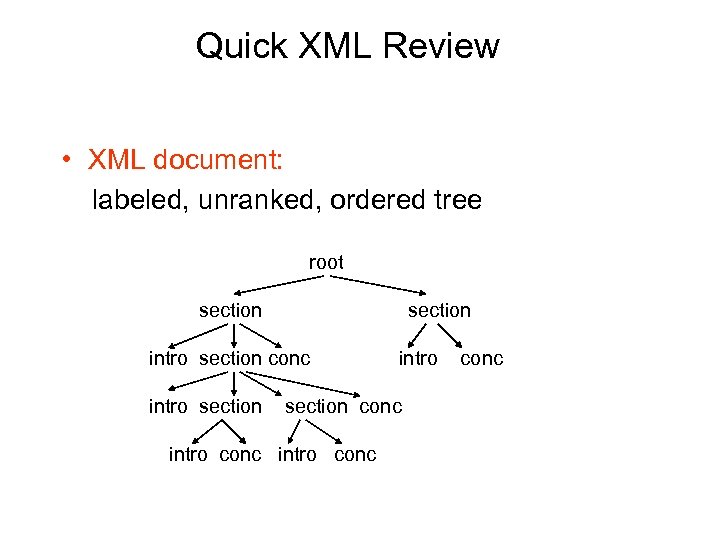
Quick XML Review • XML document: labeled, unranked, ordered tree root section intro section conc intro conc

• XML type: regular tree language • XML query: tree transducer e. g. k-pebble transducer Thomas Schwentick’s tutorial, Games’ 03
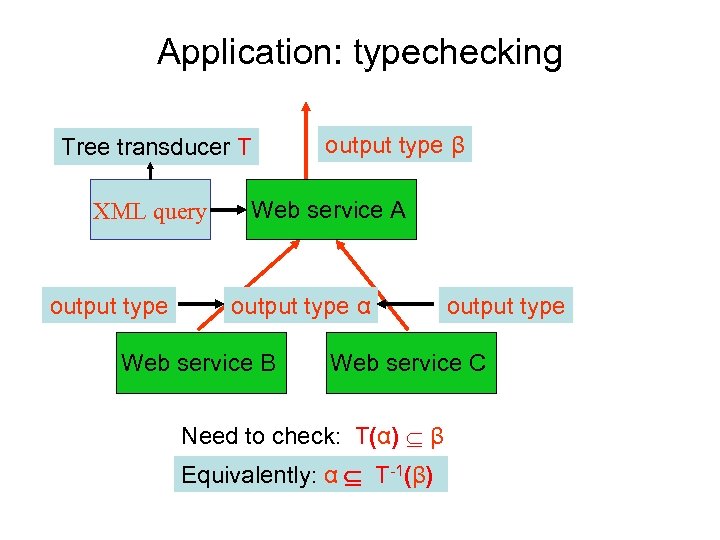
Application: typechecking Tree transducer T XML query output type β Web service A output type α Web service B output type Web service C Need to check: T(α) β Equivalently: α T-1(β)
![Theorem: T-1(β) is a regular tree language [Milo+Suciu+V. -] Typechecking: 1. Compute from T Theorem: T-1(β) is a regular tree language [Milo+Suciu+V. -] Typechecking: 1. Compute from T](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-82.jpg)
Theorem: T-1(β) is a regular tree language [Milo+Suciu+V. -] Typechecking: 1. Compute from T and β the tree automaton for T-1(β) 2. Check that α T-1(β) Caveat: no data joins
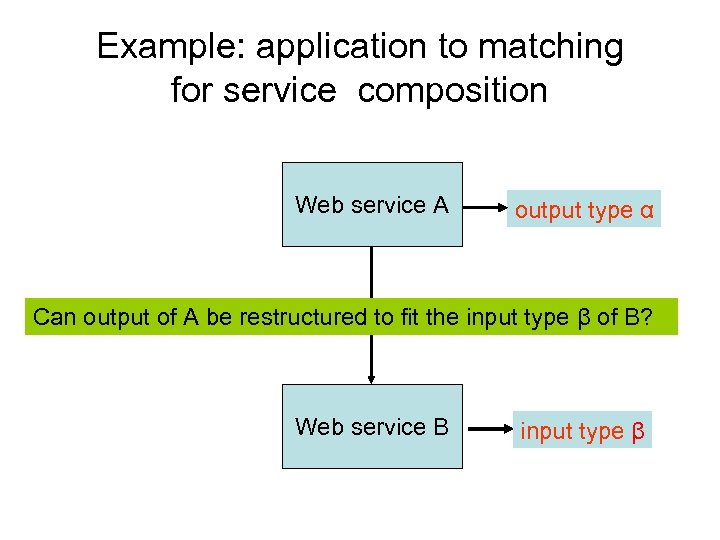
Example: application to matching for service composition Web service A output type α Can output of A be restructured to fit the input type β of B? Web service B input type β

Key: describe allowed restructurings by a nondeterministic transducer T • Given output I of service A, check whether T(I) β ≠ by constructing a tree automaton for T(I) • If yes, produce as side effect a minimal restructuring of I that satisfies β, witnessing the nonempty intersection

Static version: Can every output of A be restructured so as to satisfy the input type of B? • Key: {I / T(I) β ≠ } is regular if T is k-pebble transducer • Enough to check that α {I / T(I) β ≠ }
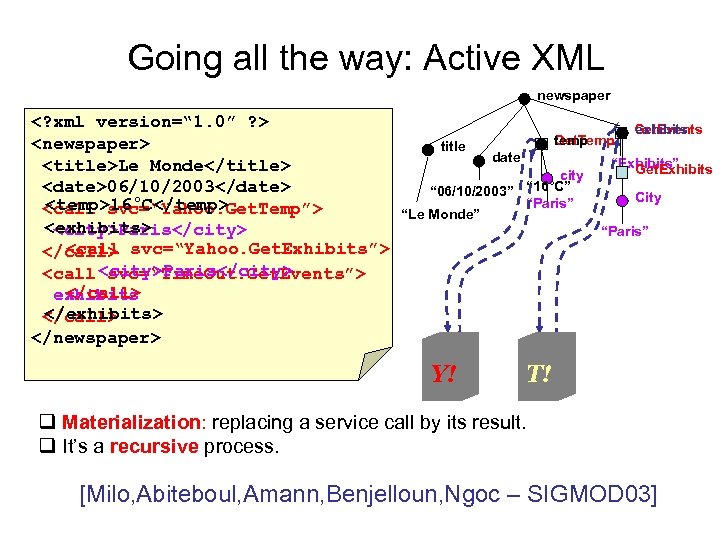
Going all the way: Active XML newspaper <? xml version=“ 1. 0” ? > <newspaper> <title>Le Monde</title> <date>06/10/2003</date> <temp>16°C</temp> <call svc=“Yahoo. Get. Temp”> <exhibits> <city>Paris</city> <call </call> svc=“Yahoo. Get. Exhibits”> <call <city>Paris</city> svc=“Time. Out. Get. Events”> </call> exhibits </exhibits> </call> </newspaper> title Get. Temp temp date city “ 16°C” “ 06/10/2003” “Paris” “Le Monde” Get. Events exhibits “Exhibits” Get. Exhibits City “Paris” Y! T! q Materialization: replacing a service call by its result. q It’s a recursive process. [Milo, Abiteboul, Amann, Benjelloun, Ngoc – SIGMOD 03]

• Context: peer-to-peer Web services • Each peer – Repository of intensional (AXML) documents – Server: provides Web services (XQuery) – Client: when invoking the embedded service calls
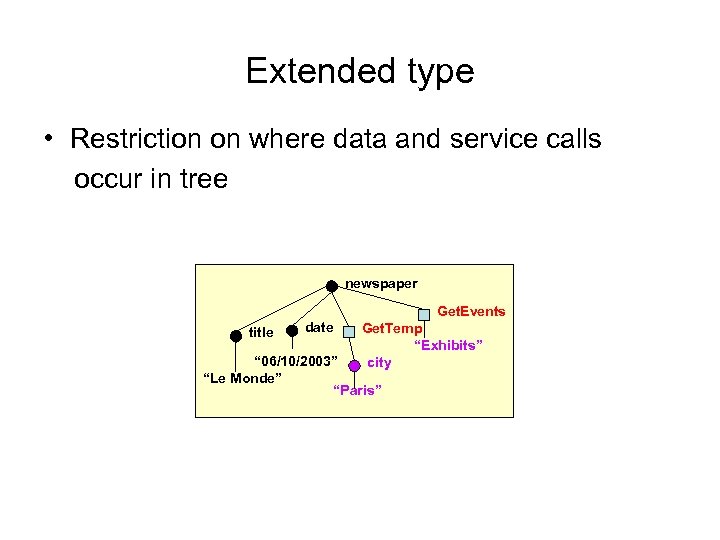
Extended type • Restriction on where data and service calls occur in tree newspaper Get. Events title date Get. Temp “Exhibits” city “ 06/10/2003” “Le Monde” “Paris”

• Service call input/output signatures • Service call definitions input parameters: XQueries on client data output: XQuery on parameters and server data

Basic typechecking problem Given AXML types and service signatures and definitions for all peers, check if: • all AXML documents resulting from calls among peers are valid • all service inputs and outputs satisfy the signatures Can be checked using transducers (if no data joins)
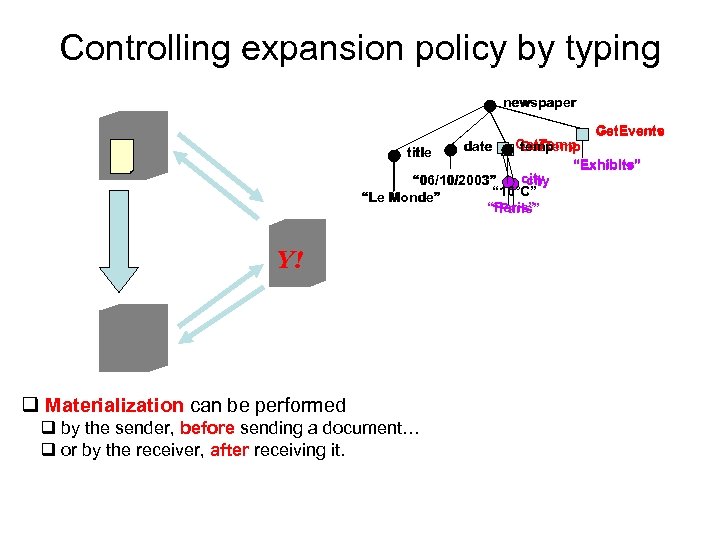
Controlling expansion policy by typing newspaper Get. Events Get. Temp temp “Exhibits” city “ 06/10/2003” “ 16°C” “Le Monde” “Paris” title Y! q Materialization can be performed q by the sender, before sending a document… q or by the receiver, after receiving it. date

Why control the materialization of calls? • For added functionality, e. g. – Intensional data allows to get up-to-date information. • For security reasons or capabilities, e. g. – – I don’t trust this Web service/domain, I don’t have the right credentials to invoke it, It costs money, Maybe the receiver doesn’t know Active XML! • For performance reasons, e. g. – A proxy can invoke services on behalf of a PDA.

Example scenario • Client allows only certain service calls, specified by its type • Can server always force its answer to satisfy the clients schema by appropriate expansions? • Game between server and invoked services

Example: word case • Client type: regular language R • Input: word a 1. . . an each ai represents a Web service call • Output type of service a: regular language Ra • Game: Bob chooses a in the current word, Alice responds with word in Ra to replace a • Bob wins if resulting word is in R Does Bob have a winning strategy on a 1. . . an ?
![Undecidable [Segoufin, Schwentick, Muscholl – STACS’ 04] even if limited to “context-free games”: Ra Undecidable [Segoufin, Schwentick, Muscholl – STACS’ 04] even if limited to “context-free games”: Ra](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-95.jpg)
Undecidable [Segoufin, Schwentick, Muscholl – STACS’ 04] even if limited to “context-free games”: Ra consists of just finitely many words Decidable under restrictions [Segoufin, Schwentick, Muscholl – STACS’ 04] [Milo, Abiteboul, Amann, Benjelloun, Ngoc – SIGMOD’ 03] complexity: PSPACE to EXPSPACE

Approaches not covered here: • • • Process algebras, pi-calculus Situation calculus Petri nets Transaction logic Use of ontologies, description logics

Thank you!
![References • [Brand Zafiropulo 83]: [15] in Hull pods 2003 • [Bulltan Fu Hull References • [Brand Zafiropulo 83]: [15] in Hull pods 2003 • [Bulltan Fu Hull](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-98.jpg)
References • [Brand Zafiropulo 83]: [15] in Hull pods 2003 • [Bulltan Fu Hull Su 03]: [17] in hull pods • [Pnueli+Rosner]: [57] in hull pods • [Kupferman + Vardi 01] [48] in hull pods • Quasi-realtime languages: accepted by non-det multitape TM in linear time [Book Greibach] also, smallest AFL containing the CFGs and closed under intersection AFL: closed under U, conc, +, non-erasing homo, inv. Homo, inters. with regular languages
![• Alternative: temporal property of sequence of exchanged messages Examples: G(( [? o] • Alternative: temporal property of sequence of exchanged messages Examples: G(( [? o]](https://present5.com/presentation/24c7d69d33759583d0d15cb9d610943c/image-99.jpg)
• Alternative: temporal property of sequence of exchanged messages Examples: G(( [? o] [ !b]) X [ !b]) “if an order has been received but a bill not yet sent, then in the next state a bill has been sent” G( [ ? o] F( [ !b] )) “if an order has been received then eventually a bill will be sent”
24c7d69d33759583d0d15cb9d610943c.ppt