42903c6d1885cbdeece7ad4def4fc371.ppt
- Количество слайдов: 50

Automatic Software Verification: A Renaissance Andrew Ireland Dependable Systems Group School of Mathematical & Computer Sciences Heriot-Watt University Edinburgh Dependable Systems Group © Andrew Ireland

Outline • • A historical perspective New wave of software verification tools Cooperative reasoning Applications and challenges Dependable Systems Group © Andrew Ireland

Assertion Based Verification • “Assertion boxes” Goldstine & von Neuman 1947 • “Checking a large routine” Turing 1949 • “Inductive assertion method” Floyd 1967 • “Axiomatic basis” Hoare 1969 • “A program verifier” King 1969 Dependable Systems Group © Andrew Ireland

Floyd’s Summation Program Dependable Systems Group © Andrew Ireland

Floyd’s Summation Program Pre-condition Post-condition Dependable Systems Group © Andrew Ireland

Floyd’s Summation Program Loop invariant Dependable Systems Group © Andrew Ireland

Floyd’s Verifying Compiler Proposal “The Verifying Compiler” CMU Annual Report p 18 -19, 1967 Dependable Systems Group © Andrew Ireland

First Wave of Verifiers • • “A Program Verifier” (King 1969) Stanford Pascal Verifier (Luckham et al 1973) Gypsy (Good et al 1974) VISTA (German & Wegbreit 1975) HDM (Levitt et al 1977) SPARK for Ada (Carre et al 1983) Penelope (Guaspari et al 1990) ESC/Java (Detlefs et al 1998) Dependable Systems Group © Andrew Ireland

So Why the Poor Uptake? • Formalizing specifications is hard • Verification requires auxiliary specifications and properties, e. g. loop invariants, inductive properties • Mechanized proof is semi-automatic at best, i. e. skilled user interaction required • Scalability issues associated with mainstream programming languages, e. g. reasoning about pointers Dependable Systems Group © Andrew Ireland

Times They Are Changing • Static Device Verifier (SDV): http: //www. microsoft. com/whdc/devtools/sdv. mspx • ESC/Java 2: http: //secure. ucd. ie/products/opensource/ESCJava 2 • Spec#: http: //research. microsoft. com/specsharp • The SPARK Approach: http: //www. praxis-his. com/sparkada Dependable Systems Group © Andrew Ireland

What’s Changed? • Generic property verification “Buffer overflows have been the most common form of security vulnerability for the past 10 years“ OGI/DARPA • • Programming language subsets Programming logics Automated reasoning tools Tool integrations Dependable Systems Group © Andrew Ireland
Cooperative Reasoning + Dependable Systems Group = © Andrew Ireland
Cooperative Reasoning + Dependable Systems Group = © Andrew Ireland

Cooperative Reasoning + = = Complementary techniques compensating for each other’s weaknesses Dependable Systems Group © Andrew Ireland

Reliable & Safe Ada Subsets “It is not too late! I believe that by careful pruning of the Ada language, it is still possible to select a very powerful subset that would be reliable and efficient in implementation and safe and economic to use” C. A. R. Hoare 1980 ACM Turing Award Lecture Dependable Systems Group © Andrew Ireland

The SPARK Approach • A subset of Ada that eliminates potential ambiguities and insecurities (PRAXIS) • Expressive enough for industrial applications, but restrictive enough to support rigorous analysis • SPARK toolset supports data & information flow analysis and formal verification • Partial correctness & exception freedom proof, e. g. proving code is free from buffer overflows, range violations, division by zero. Dependable Systems Group © Andrew Ireland

SPARK Applications • Advanced avionics (Eurofighter Typhoon), transportation, air traffic control, security (MONDEX) • Ship Helicopter Operating Limits Information System (SHOLIS): first system developed to meet UK MOD Defence Standard 00 -55 • Supports “correctness-by-construction” and is advocated by US National Cyber Security Partnership (NSA) as one of three software development processes that can deliver sufficient assurance for security critical systems Dependable Systems Group © Andrew Ireland
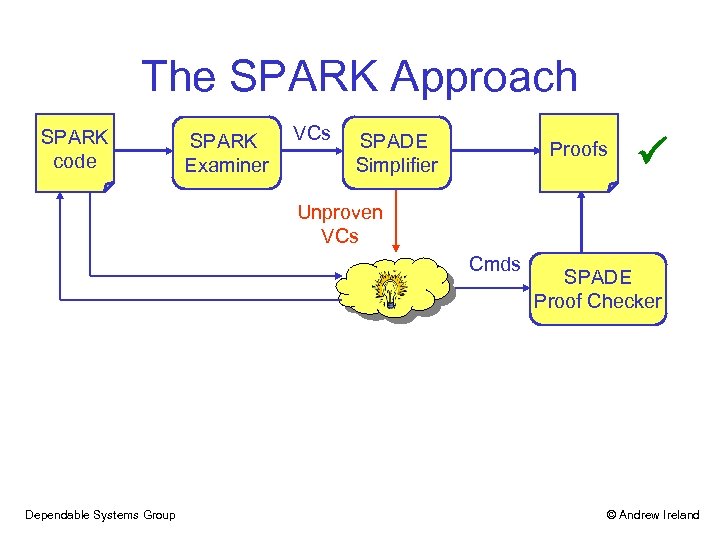
The SPARK Approach SPARK code SPARK Examiner VCs SPADE Simplifier Proofs Unproven VCs Cmds Dependable Systems Group SPADE Proof Checker © Andrew Ireland
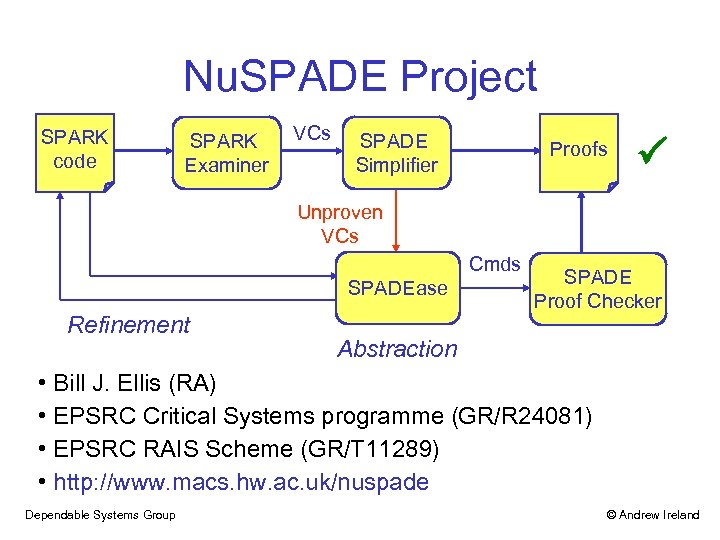
Nu. SPADE Project SPARK code SPARK Examiner VCs SPADE Simplifier Proofs Unproven VCs Cmds SPADEase Refinement SPADE Proof Checker Abstraction • Bill J. Ellis (RA) • EPSRC Critical Systems programme (GR/R 24081) • EPSRC RAIS Scheme (GR/T 11289) • http: //www. macs. hw. ac. uk/nuspade Dependable Systems Group © Andrew Ireland

SPADEase Program Analysis Proof Planning • Exception freedom proofs • Automatic loop invariant discovery Dependable Systems Group © Andrew Ireland

Proof Planning Conjecture Theory Method Critic Proof Planner Tactic Proof Checker Dependable Systems Group Proof © Andrew Ireland

Proof Planning • Reuse: strategies can be easily ported between checkers • Robustness: critics and middle-out reasoning provide flexibility in how proof search is organized • Cooperation: planning provides a natural level at which to combine multiple reasoning processes Dependable Systems Group © Andrew Ireland
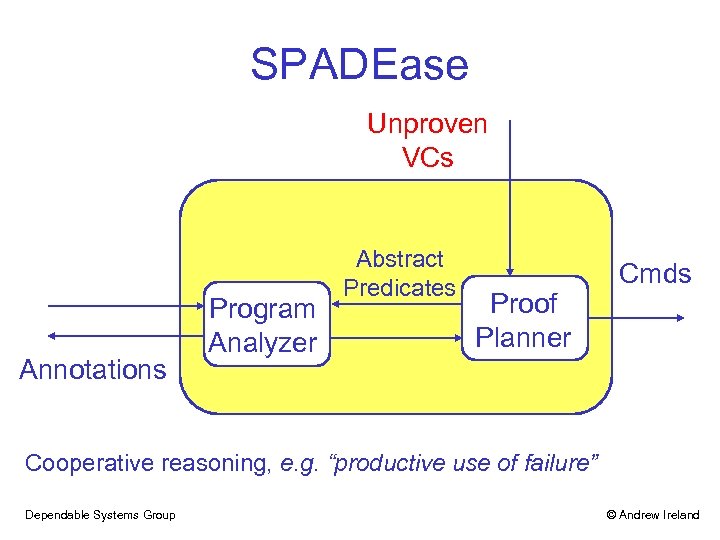
SPADEase Unproven VCs Annotations Program Analyzer Abstract Predicates Proof Planner Cmds Cooperative reasoning, e. g. “productive use of failure” Dependable Systems Group © Andrew Ireland

An Example subtype AR_T is Integer range 0. . 9; type A_T is array (AR_T) of Integer; . . . procedure Filter(A: in A_T; R: out Integer) is begin R: =0; for I in AR_T loop if A(I)>=0 and A(I)<=100 then R: =R+A(I); end if; end loop; end Filter; Dependable Systems Group © Andrew Ireland

Exception Freedom VC. . . H 1: for_all (i___1: integer, ((i___1 >= ar_t__first) and (i___1 <= ar_t__last)) -> H 4: element(a, [loop__1__i]) >= 0. ((element(a, [i___1]) >= integer__first) and (element(a, [i___1]) <= integer__last))). H 5: element(a, [loop__1__i]) <= 100. H 2: loop__1__i >= ar_t__first. H 3: loop__1__i <= ar_t__last. H 6: r >= integer__first H 4: element(a, [loop__1__i]) >= 0. . H 7: r <= integer__last. H 5: element(a, [loop__1__i]) <= 100. H 6: r >= integer__first. H 7: r <= -> integer__last. -> . . . C 1: r + element(a, [loop__1__i]) >= integer__first. C 2: r + element(a, [loop__1__i]) <= integer__last. . . . C 3: loop__1__i >= ar_t__first. C 4: loop__1__i <= ar_t__last. Dependable Systems Group © Andrew Ireland

Exception Freedom VC. . . H 1: for_all (i___1: integer, ((i___1 >= ar_t__first) and (i___1 <= ar_t__last)) -> H 4: element(a, [loop__1__i]) >= 0. ((element(a, [i___1]) >= integer__first) and (element(a, [i___1]) <= integer__last))). H 5: element(a, [loop__1__i]) <= 100. H 2: loop__1__i >= ar_t__first. H 3: loop__1__i <= ar_t__last. H 6: r >= integer__first -32768 H 4: element(a, [loop__1__i]) >=. 0. . H 5: element(a, [loop__1__i]) <= 100. 32767. H 7: r <= integer__last. H 6: r >= integer__first. H 7: r <= -> integer__last. -> . . . C 1: r + element(a, [loop__1__i]) >= integer__first. C 2: r + element(a, [loop__1__i]) <= integer__last 32767. . C 3: loop__1__i >= ar_t__first. C 4: loop__1__i <= ar_t__last. Dependable Systems Group © Andrew Ireland

Exception Freedom VC. . . H 1: for_all (i___1: integer, ((i___1 >= ar_t__first) and (i___1 <= ar_t__last)) -> H 4: element(a, [loop__1__i]) >= 0. ((element(a, [i___1]) >= integer__first) and (element(a, [i___1]) <= integer__last))). H 5: element(a, [loop__1__i]) <= 100. H 2: loop__1__i >= ar_t__first. H 3: loop__1__i <= ar_t__last. H 6: r >= integer__first -32768 H 4: element(a, [loop__1__i]) >=. 0. . If (32668 <= r <= 32767) then H 5: element(a, [loop__1__i]) <= 100. 32767. H 7: r <= integer__last. possible overflow, i. e. VC is H 6: r >= integer__first. unprovable -> H 7: r <= integer__last. -> . . . C 1: r + element(a, [loop__1__i]) >= integer__first. C 2: r + element(a, [loop__1__i]) <= integer__last. <= 32767. . C 3: loop__1__i >= ar_t__first. C 4: loop__1__i <= ar_t__last. Dependable Systems Group © Andrew Ireland

Proof-Failure Analysis • Preconditions: 1. Unproven relational goal of the form E Rel C, e. g. r + element(a, [loop__1__i]) <= 32767 2. Given the constraints on E, a counter-example can be found that shows bounds are insufficient to prove exception freedom, e. g. r >= -32768 and r <= 32767 • Patch: Dependable Systems Group R >= ? and R <= ? © Andrew Ireland
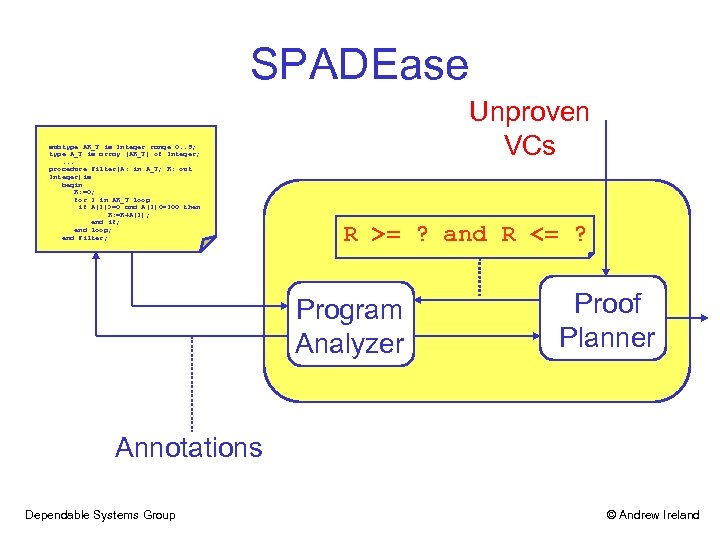
SPADEase subtype AR_T is Integer range 0. . 9; type A_T is array (AR_T) of Integer; . . . procedure Filter(A: in A_T; R: out Integer)is begin R: =0; for I in AR_T loop if A(I)>=0 and A(I)<=100 then R: =R+A(I); end if; end loop; end Filter; Unproven VCs R >= ? and R <= ? Abstract Predicates Program Analyzer Proof Planner Annotations Dependable Systems Group © Andrew Ireland
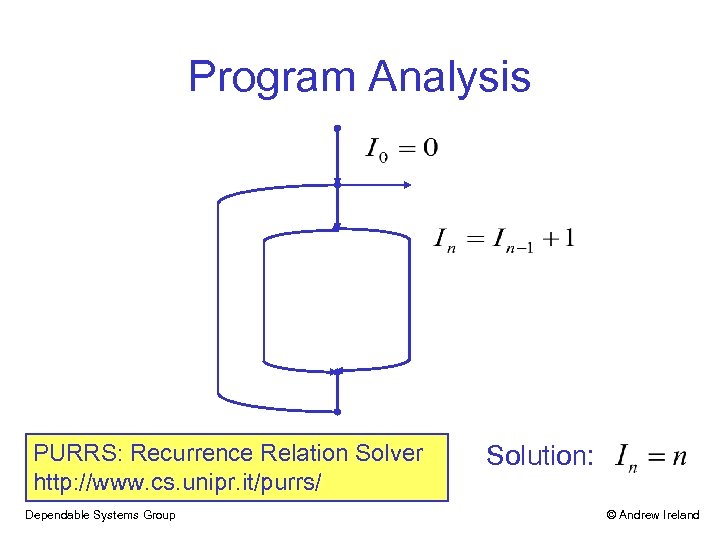
Program Analysis PURRS: Recurrence Relation Solver http: //www. cs. unipr. it/purrs/ Dependable Systems Group Solution: © Andrew Ireland

Program Analysis Dependable Systems Group © Andrew Ireland
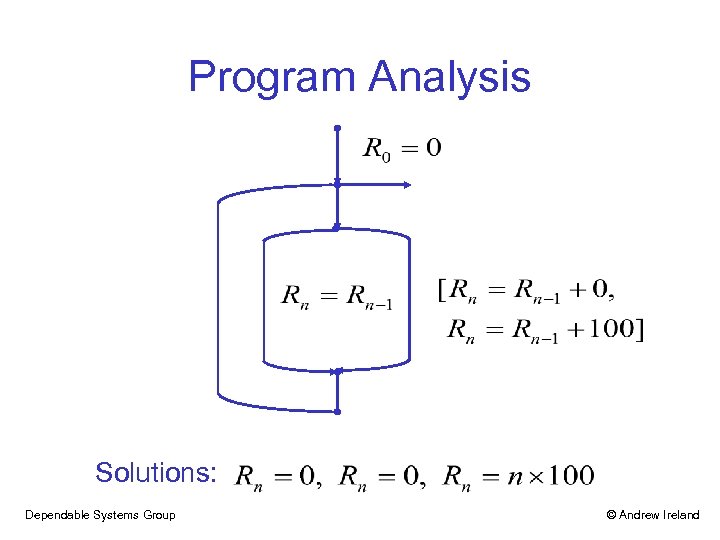
Program Analysis Solutions: Dependable Systems Group © Andrew Ireland

Combining Solutions --# assert R >= 0 and R <= I*100 Dependable Systems Group © Andrew Ireland

SPADEase subtype AR_T is Integer range 0. . 9; subtype AR_Tarray (AR_T)range 0. . 9; type A_T is is Integer of Integer; type A_T is array (AR_T) of Integer; . . . procedure Filter(A: in A_T; R: out Integer)is begin R: =0; in AR_T loop for I in AR_T >= 0 and R <= I*100 --# assert R loop if A(I)>=0 and A(I)<=100 then R: =R+A(I); end if; end loop; end Filter; Unproven VCs R >= ? and R <= ? Abstract Predicates Program Analyzer Proof Planner Annotations --# assert R >= 0 and R <= I*100 Dependable Systems Group © Andrew Ireland

Revised Filter Code subtype AR_T is Integer range 0. . 9; type A_T is array (AR_T) of Integer; . . . procedure Filter(A: in A_T; R: out Integer) is begin R: =0; for I in AR_T loop --# assert R >= 0 and R <= I*100 if A(I)>=0 and A(I)<=100 then R: =R+A(I); end if; end loop; end Filter; Dependable Systems Group © Andrew Ireland

Revised Exception Freedom VC H 1: r >= 0. H 2: r <= loop__1__i * 100. . . . H 3: for_all (i___1: integer, ((i___1 >= ar_t__first) and (i___1 <= ar_t__last)) -> ((element(a, [i___1]) >= integer__first) and (element(a, [i___1]) <= integer__last))). H 6: element(a, [loop__1__i]) >= 0. H 4: loop__1__i >= ar_t__first. H 5: loop__1__i <= ar_t__last. H 7: element(a, [loop__1__i]) <= 100. H 6: element(a, [loop__1__i]) >= 0. H 7: element(a, [loop__1__i]) <= 100. … H 8: r >= integer__first. -> H 9: r <= integer__last. -> Transitivity proof plan . . . C 1: r + element(a, [loop__1__i]) >= integer__first. C 2: r + element(a, [loop__1__i]) <= integer__last. C 3: loop__1__i >= ar_t__first. . C 4: loop__1__i <= ar_t__last. Dependable Systems Group © Andrew Ireland
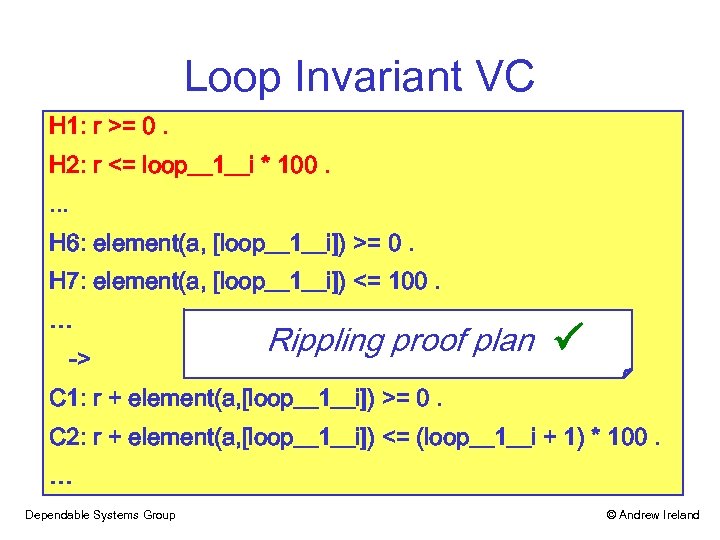
Loop Invariant VC H 1: r >= 0. H 2: r <= loop__1__i * 100. . H 6: element(a, [loop__1__i]) >= 0. H 7: element(a, [loop__1__i]) <= 100. … -> Rippling proof plan C 1: r + element(a, [loop__1__i]) >= 0. C 2: r + element(a, [loop__1__i]) <= (loop__1__i + 1) * 100. … Dependable Systems Group © Andrew Ireland
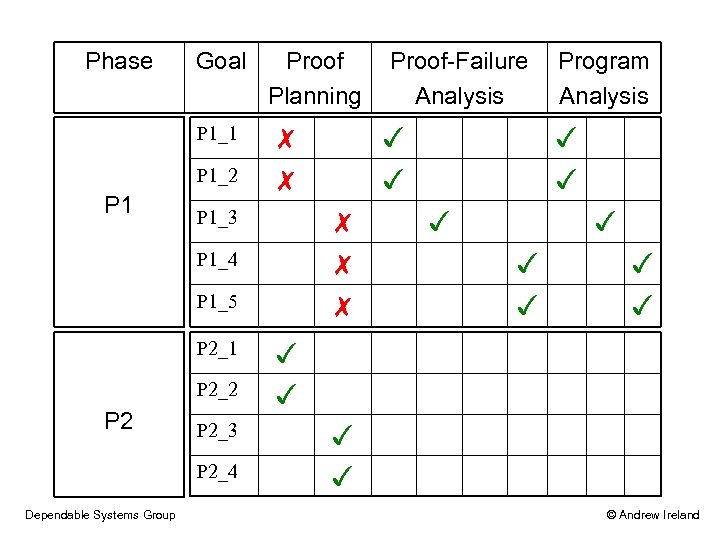
Phase Goal P 1_1 P 1_2 P 1 Proof Planning P 1_3 ✗ P 1_4 ✗ ✗ P 1_5 P 2_1 P 2_2 P 2_3 P 2_4 Dependable Systems Group Program Analysis ✓ ✓ ✗ ✗ Proof-Failure Analysis ✓ ✓ ✓ © Andrew Ireland

Nu. SPADE Results • Our evaluation was based upon examples drawn from industrial data provided by Praxis, e. g. SHOLIS • SPADE Simplifier is very effective on exception freedom VC, i. e. typical hit-rate of 92% • SPADEase targeted the VCs which the SPADE Simplifier failed to prove, i. e. loop-based code • While critical software is engineered to minimize the number and complexity of loops, we found that 80% of the loops we encountered were provable using SPADEase Dependable Systems Group © Andrew Ireland
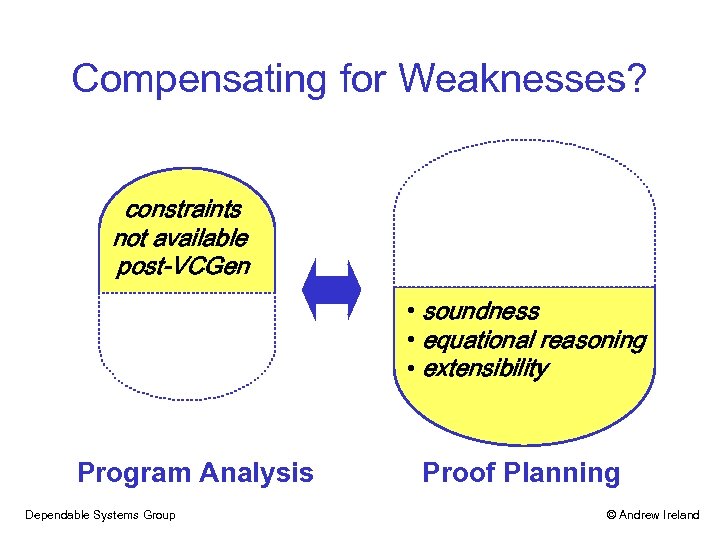
Compensating for Weaknesses? constraints not available post-VCGen • soundness • equational reasoning • extensibility Program Analysis Dependable Systems Group Proof Planning © Andrew Ireland

Limitations & Related Work • Constraint solving fails when reasoning with “big numbers”, i. e. integers out with –(225)… 225 -1 • Precondition strengthening would improve our hit-rate, constraint solving may have a role to play. • Integrating decision procedures with SPADEase would also improve hit-rate. • Paul Jackson, Bill J. Ellis, Kathleen Sharp “Using SMT Solvers to Verify High-Integrity Programs” 2 nd Int. Workshop on Automated Formal Methods (AFM-07) • Boulton, Bundy, Gordon, Slind Clam/HOL Project (`96 -`99) Dependable Systems Group © Andrew Ireland

SPADEase Impact? “… It increases the proportion of SPARKgenerated verification conditions that can be proved automatically without introducing any new opaque, black-box processes. …” Peter Amey Chief Technical Officer Praxis High Integrity Systems Dependable Systems Group © Andrew Ireland

SPADEase Impact? “… The separation of proof planning from proof checking also acts as a talent multiplier by allowing proof experts to spend their time creating new and reusable methods and approaches rather than working on individual proofs. ” Peter Amey Chief Technical Officer Praxis High Integrity Systems Dependable Systems Group © Andrew Ireland

CORE Project • Separation Logic: Reynolds (CMU) & O’Hearn (QMU) • Focuses the reasoning effort on only those parts of the heap that are relevant to a program unit, i. e. local reasoning • CORE Project: – Ewen Maclean (Post Doc) & Ianthe Hind (Ph. D) – EPSRC EP/F 037597 – http: //www. macs. hw. ac. uk/core • Building upon shape analysis tools, CORE aims to automate the verification of functional properties Dependable Systems Group © Andrew Ireland

Compensating for Weaknesses? shape properties • content properties • soundness • extensibility Symbolic Execution (Smallfoot. RG) Dependable Systems Group Proof Planning (Isa. Planner) © Andrew Ireland

CORE Challenges Automating “eureka” steps: • Loop invariants • Frame axioms • Auxiliary inductive lemmas • Existential witnesses Note: details via Tech Talks at Google Dependable Systems Group © Andrew Ireland
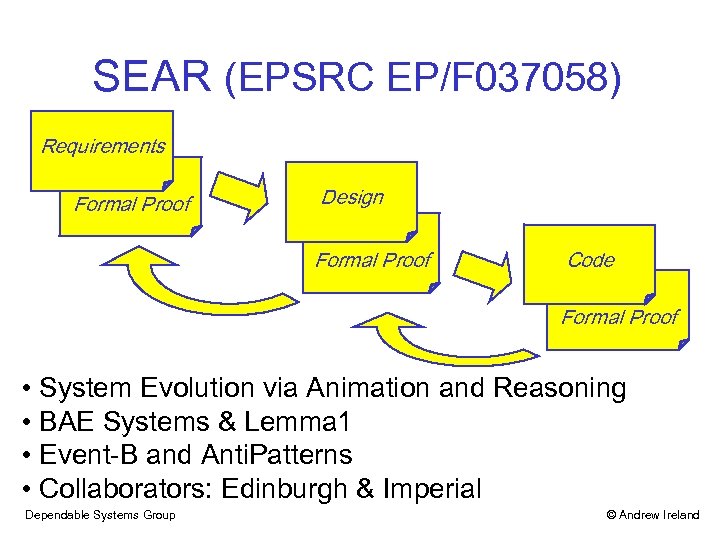
SEAR (EPSRC EP/F 037058) Requirements Formal Proof Design Formal Proof Code Formal Proof • System Evolution via Animation and Reasoning • BAE Systems & Lemma 1 • Event-B and Anti. Patterns • Collaborators: Edinburgh & Imperial Dependable Systems Group © Andrew Ireland

Grand Challenges • UK GC 6: Dependable Systems Evolution (a collaboration with the International Verified Software Grand Challenge) • Verifying Compiler Grand Challenge – Hoare • The Verified Software Repository – Woodcock: • accelerate the development of verification tools • open access to challenge problems and results • Industry engagement • http: //vsr. sourceforge. net/Introduction. htm Dependable Systems Group © Andrew Ireland

Conclusion • A new wave of software verification tools is emerging within a range of niche markets • Technological advances and the economics of software failures have been major drivers • Cooperation: tools and communities • Grand Challenge or Emerging Technology? • As Automated Verification researchers we are challenged by a grand opportunity! Dependable Systems Group © Andrew Ireland

And Finally … 3 rd IFIP Working Conference on Verified Software: Theories, Tools & Experiments hosted by Heriot-Watt University August 16 th-19 th, 2010 http: //www. macs. hw. ac. uk/vstte 10 Dependable Systems Group © Andrew Ireland
42903c6d1885cbdeece7ad4def4fc371.ppt