AUTOMATIC CONTROL THEORY.pptx
- Количество слайдов: 61

AUTOMATIC CONTROL THEORY

References • B. C. Kuo, F. Golnaragi. Automatic control systems, 8/e, – Wiley, 2002, 624 p. • G. F. Franklin, J. D. Powell. , Abbas Emami. Naeini. Feedback control of dynamic systems. Prentice Hall, 2002, 910 p. • Katsuhiko Ogata. Modern control engineering. Prentice Hall, 4/e, 2001, 970 p. • R. Rinkevičienė. Automatinio valdymo teorija. Sistemų analizė ir sintezė. Vilnius, Technika, 1999. – 67 p. • Norman S. Nise. Control system Engineering. 4 th edition. John Wiley and Sons, Inc. 2004, 983 p. • John Van de Vegte. Feedback control systems. Prentice Hall, 1994, 452 p.

• Automatic Control Systems change life in all advanced societies today. Technological developments have made it possible to travel to the moon; explore outer space. And the successful operation of space vehicle; the space shuttle; space station; robot; industry control, such as the control of temperature, pressure, fluid, lever, speed of the motor and so on.

Historical review The first automatic feedback controller used in an industrial process is generally agreed to be James Watt’s flyball governor, developed in 1769 for controlling the speed of a steam engine.

• The all-mechanical device, measured the speed of the output shaft and utilized the movement of the flyball with speed to control the valve and therefore the amount of steam entering the engine. As the speed increases, the ball weights rise and move away from the shaft axis, thus closing the valve. The flyweights require power from the engine to turn and therefore cause the speed measurement to be less accurate.
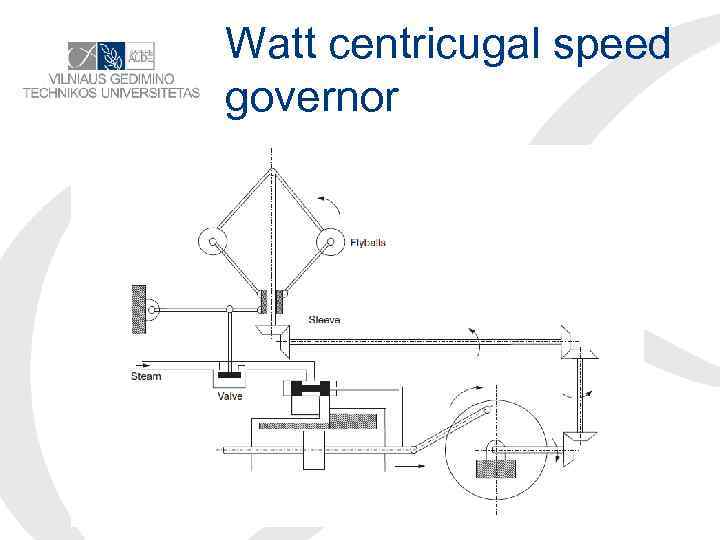
Watt centricugal speed governor

• J. C. Maxwell formulated a mathematical theory related to control theory using a differential equation model of a governor. (1868) • Conventional control theory is effectively applied to many control design problems, especially to single input – single output (SISO) systems. Its mathematical foundation is the Laplace transform.

• Routh 1884; Hurwitz 1895, algebra • stability criterion; • 1932, Nyquist, steady-state frequency response techniques; • 1927, Bode and Nichols, frequency response • analysis; • 1948, Evans, root-locus theory; • A. M. Lyapunov, stability theory.

• Modern control theory (1960) is based on state variable methods, for the design of multiple-input multiple-output (MIMO) systems. • Wiener(1949), Optimum design. • Bellman(1957), Dynamic programming. • Pontryagin(1962), Maximum principle. • Kalman(1960), Controllability and observability • Kalman and Buey(1961), Combination of optimal filter and optimal controller, Linear quadratic Gaussian(LQG) control.

Definitions • A control system is an interconnection of components forming a system configuration that will provide a desired system response. Reference input (Desired output) Excitation applied to a control system from an external source. The reference signal is produced by the reference source. It is the actual signal input to control system.

• • Advanced control theory(1980) Robust theory. (1980 s) Intelligent control theory: Artificial Neural Networks(ANNS); Fuzzy Control(FC); Expert System(ES). GA, GP, EC, Chaos etc
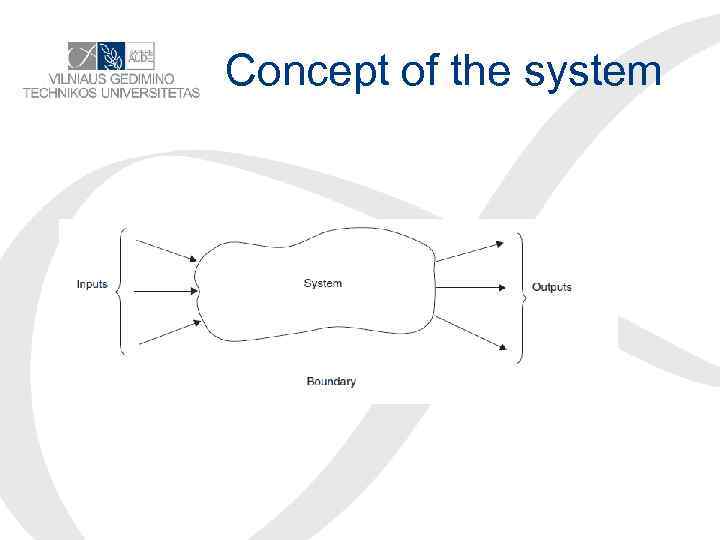
Concept of the system

Disturbance, output, feedback • Disturbance input: A disturbance input signal to the system that has an unwanted effect on the system output. • Output (controlled variable ): The quantity that must be maintained at a prescribed value, i. e. , it must follow the command input without responding to disturbance inputs. • Feedback: The output of a system that is returned to modify the input.
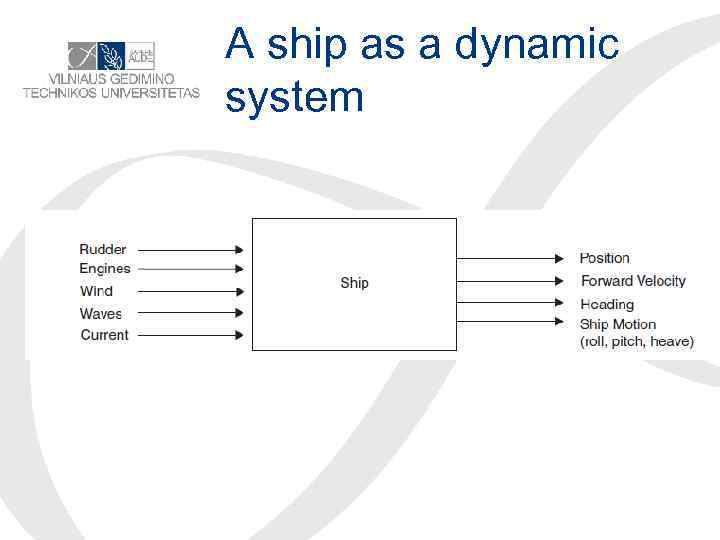
A ship as a dynamic system

• Error: The difference between the input and the output. Open-loop control system: A system in which the output has no effect upon the input signal. Feedback element: The unit provides the measurement value for feeding back the output quantity, or a function of the output, in order to compare it with the reference.
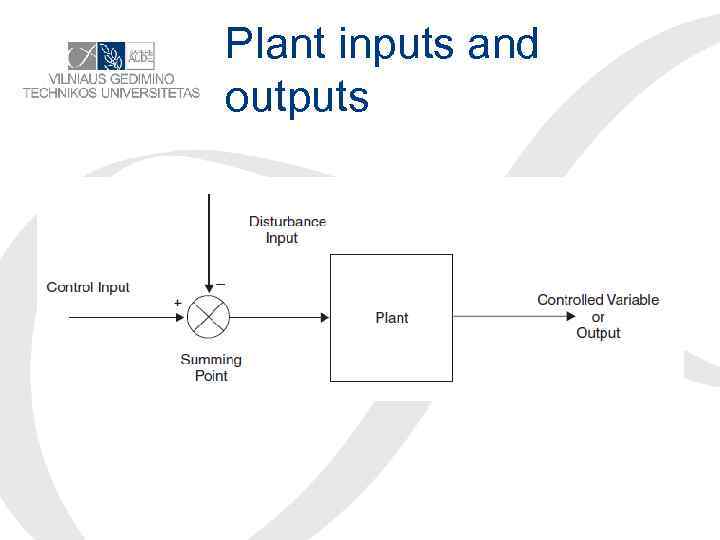
Plant inputs and outputs

Signals • Actuating signal (error signal): The signal that is the difference between the reference input and the feedback signal. It is the input to the control unit that causes the output to have the desired value. • Negative feedback: The output signal is feed back so that it subtracts from the input signal.

Closed loop system • Closed-loop control system: A system in which the output has an effect upon the input quantity in such a manner as to maintain the desiredoutput value. • That is, a system that uses a measurement of the output and compares it with the desired output , set up by reference signal.

Automation • • Control systems are used to achieve: (1) increased productivity; (2) improved performance of a device or system. The control of an industrial process (manufacturing, production, and so on) by automatic rather than manual means is often called automation. • Automation is used to improve productivity and obtain high-quality products.
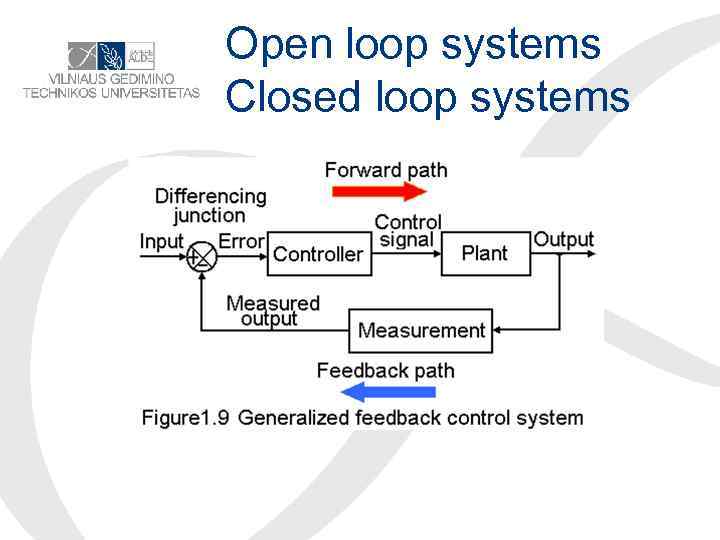
Open loop systems Closed loop systems
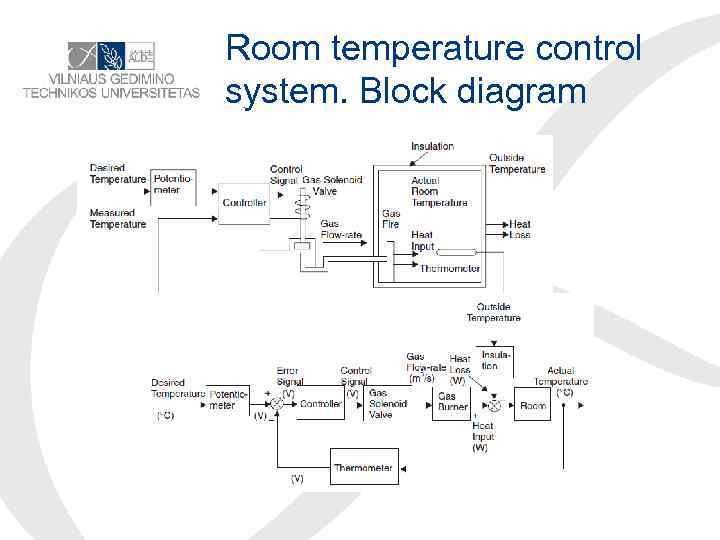
Room temperature control system. Block diagram
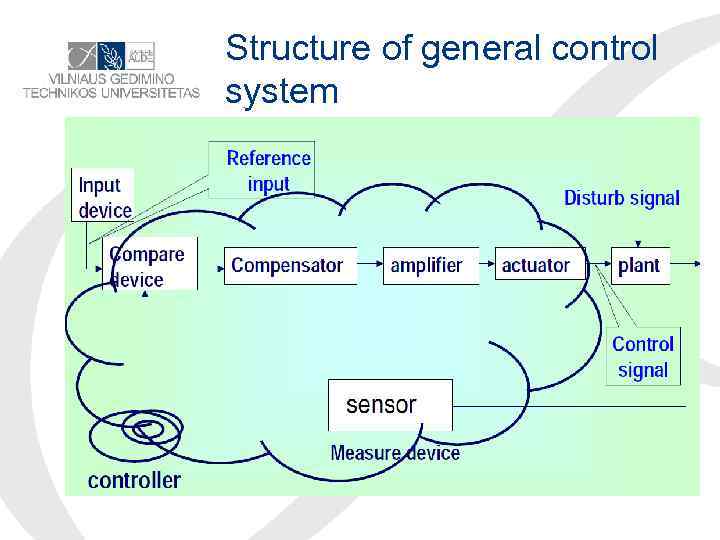
Structure of general control system
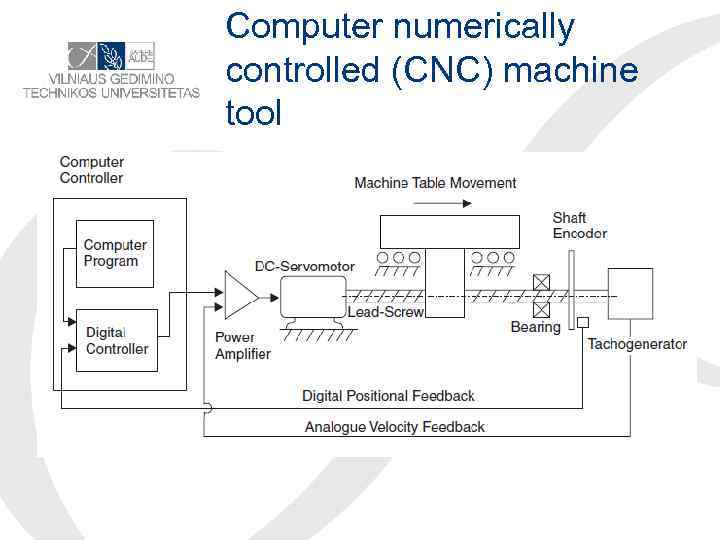
Computer numerically controlled (CNC) machine tool
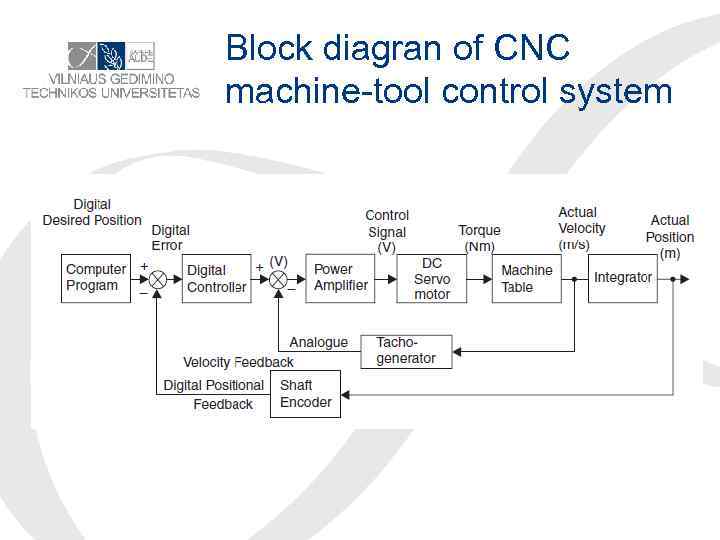
Block diagran of CNC machine-tool control system

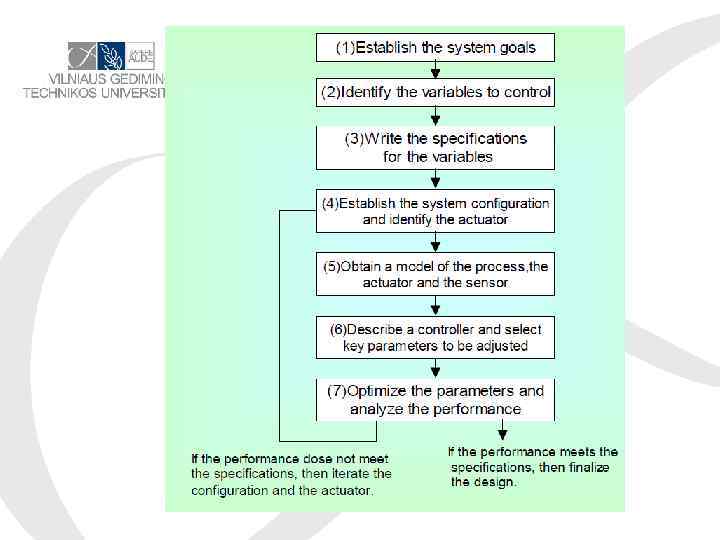
Control system design process

Classify of Control System • The form of system’s mathematics model • Linear system/ Nonlinear system: the dynamic equation of system is linear differential equation/nonlinear differential equation. • A linear system satisfies the principle of superposition.

Time-varying system and time-invariant system • Time-varying system is a system for which one or more of the parameters of the system may vary as a function of time. • 2. Reference input • r(t)=constant r(t)=f(t • can be known • the vary rule f(t) • cann’t be known “servo”

General knowledges • 1) Knowledge of the desired value: • It is necessary to know what it is you are trying to control.

2) Knowledge of the output or actual value • This must be measured by a feedback sensor again in a form suitable for the controller to understand. • In additional, the sensor must have the necessary resolution and dynamic response , so that the measured value has accuracy required from the performance specification.

3) Knowledge of the controlling device • The controller must be able to accept measurements of desired and actual values and compute a control signal in a suitable form to drive an actuating element.

SYSTEM MODELLING

If the dynamic behaviour of a physical system can be represented by an equation, or a set of equations, this is referred to as the mat hematical model of the system. Models can be constructed from knowledge of the physical characteristics of the system, i. e. mass for a mechanical system or resistance for an electrical system. Alternatively, a mathematical model may be determined by experimentation measuring how the system output responds to known inputs.

Mathematical models of systems • • • Types of mathematical models: 1) Differential equations 2) Transfer function 3) Block diagram, signal flow graph 4) State variables (modern control theory)

Differential equations with constant coeficients
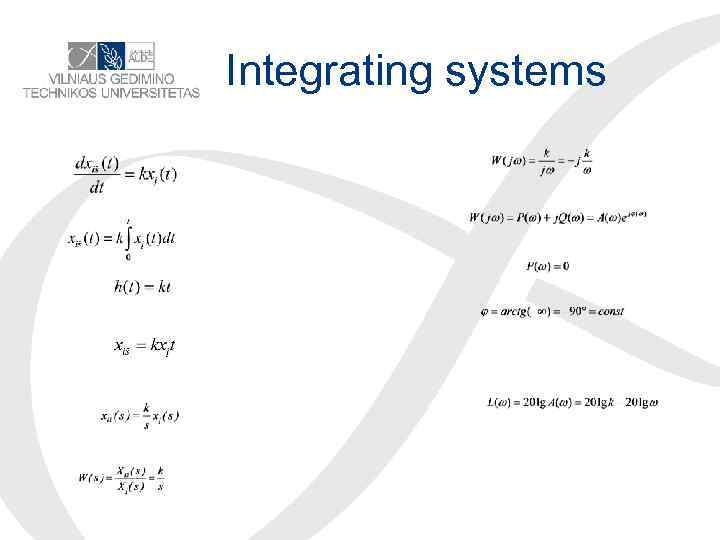
Integrating systems
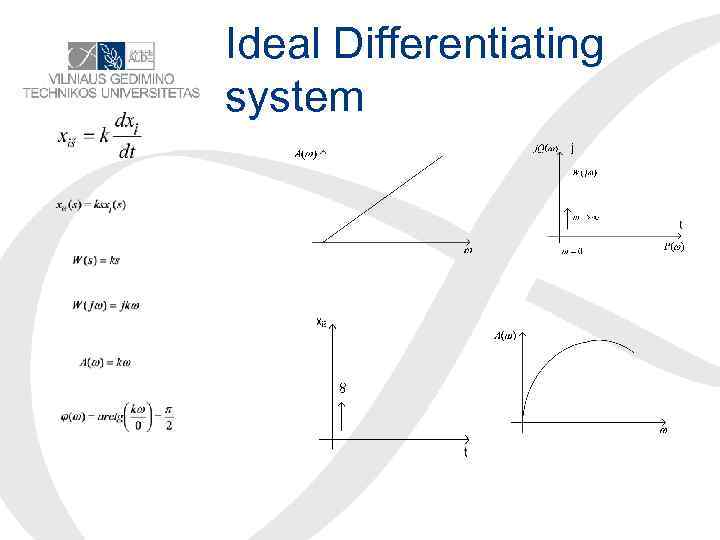
Ideal Differentiating system


Mathematical models of systems Example 2. 1 : A passive circuit input → ur output → uc。 :

Mathematical models of systems Example 2. 2 : A mechanism Define: input → F ,output → y. We have: Compare with example 2. 1: uc→y; ur→F ─ analogous systems

Mathematical models of the systems • Steps to obtain the input-output description (differential equation) of control systems: • 1) Determine the output and input variables of the control systems • 2) Write the differential equations of each system’s components in terms of the physical laws of the components. • 3) dispel the intermediate(across) variables to get the input-output description which only contains the output and input variables.

4) Formalize the input-output equation to be the “standard” form: Input variable —— on the right of the input-output equation. Output variable —— on the left of the input-output equation. Writing polynomial—— according to the falling-power order. General form of the input-output equation of the linear control systems—a nth-order differential equation:

Transfer function definition • Transfer function is the ratio of the Laplace transform of the output variable to the Laplace transform of the input variable, with all initial condition assumed to be zero and for the linear systems, that is • C(s) — Laplace transform of the output variable • R(s) — Laplace transform of the input variable • G(s) — transfer function

Mathematical models of systems • Transfer funtions are mainly derived from mathematical models of the system:

Transfer function of the typical elements of linear systems

Proportioning element A linear system can be regarded as the composing of several typical elements, which are: proportioning, inertia, integrating, differentiating, oscillating and delay elements. Relationship between the input and output variables: Transfer function: Block diagram representation and unit step response: Examples: amplifier, gear train, tachometer…

Inertial element Relationship between the input and output variables: Transfer function: Block diagram representation and unit step response: Examples: inertia wheel, inertial load (such as temperature system), electric motor…
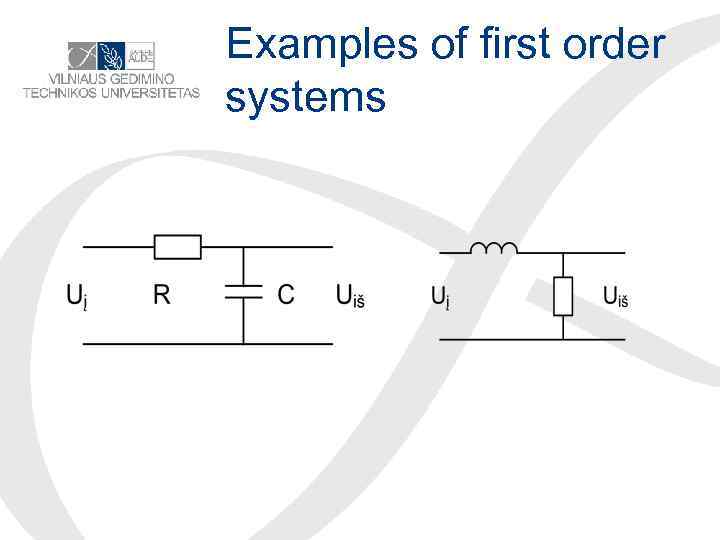
Examples of first order systems
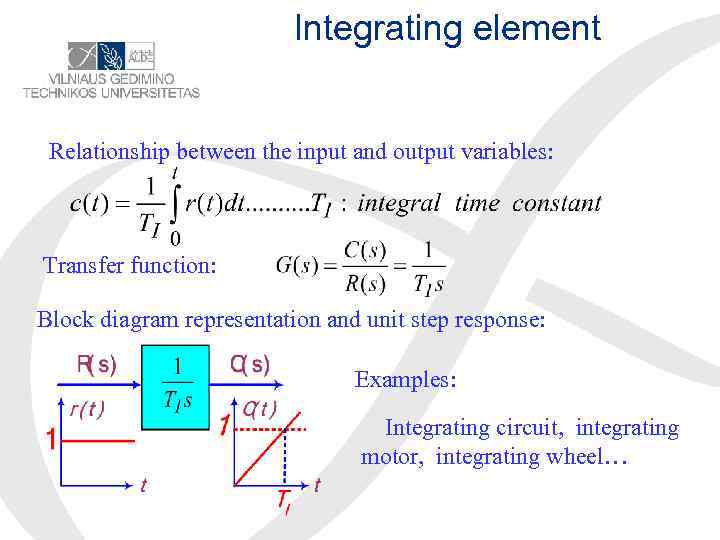
Integrating element Relationship between the input and output variables: Transfer function: Block diagram representation and unit step response: Examples: Integrating circuit, integrating motor, integrating wheel…


Differentiating element

Mathematical models of systems 2. 5. 5 Oscillating element Relationship between the input and output variables: Transfer function: Block diagram representation and unit step response: Examples: oscillator, oscillating table, oscillating circuit…

Mathematical models of systems 2. 5. 6 Delay element Relationship between the input and output variables: Transfer function: Block diagram representation and unit step response: Examples: gap effect of gear mechanism, threshold voltage of transistors…

Frequency response • Inertial element

Frequency response
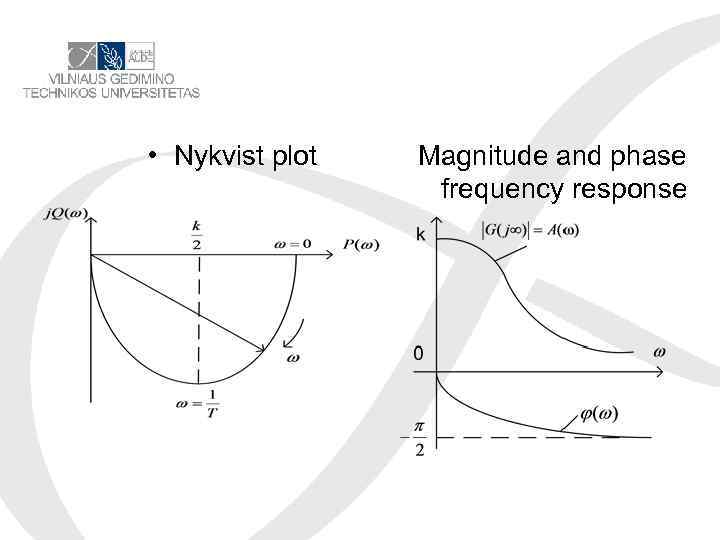
• Nykvist plot Magnitude and phase frequency response

Bode plots
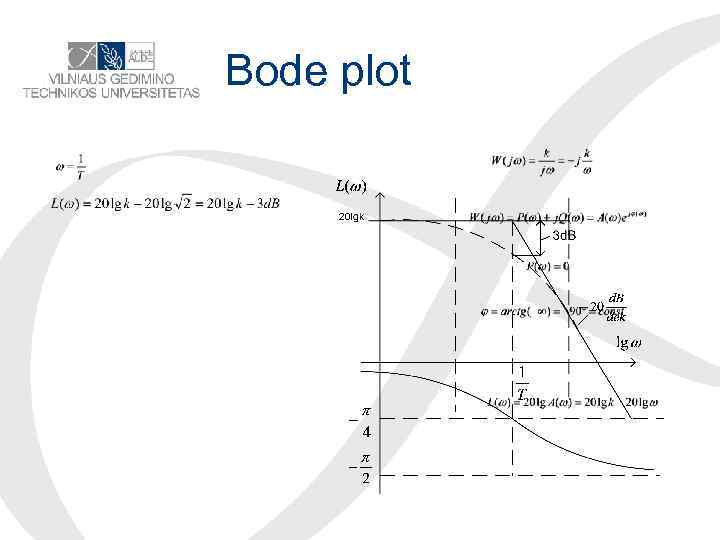
Bode plot
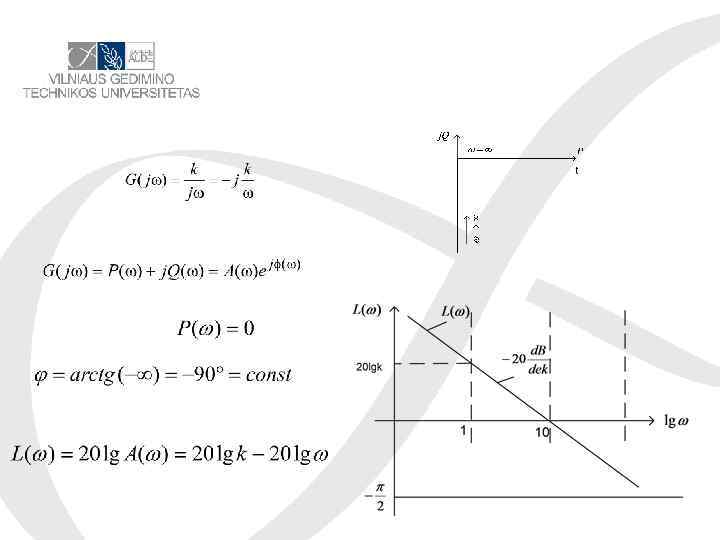

Real differentiating system •
AUTOMATIC CONTROL THEORY.pptx