Automatic Assumption Generation for Compositional Verification Dimitra Giannakopoulou

Automatic Assumption Generation for Compositional Verification Dimitra Giannakopoulou (RIACS), Corina Păsăreanu (Kestrel) Automated Software Engineering NASA Ames Research Center Moffett Field, CA, USA

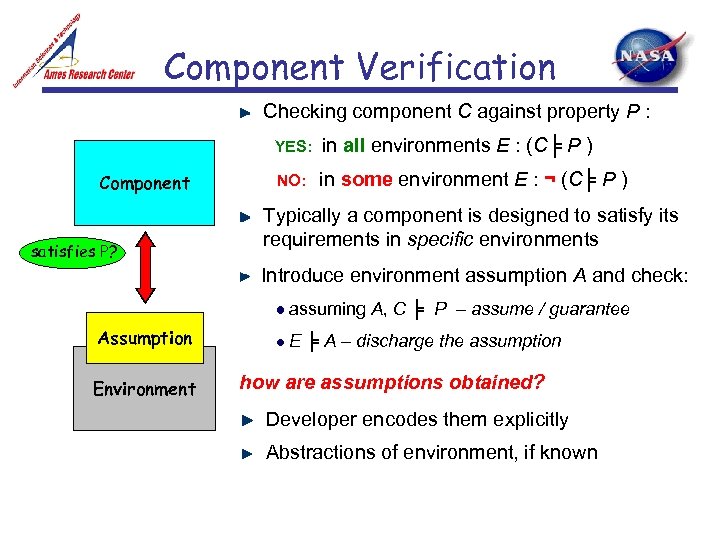Component Verification Checking component C against property P : YES: Component satisfies P? in all environments E : (C╞ P ) NO: in some environment E : ¬ (C╞ P ) Typically a component is designed to satisfy its requirements in specific environments Introduce environment assumption A and check: assuming A, C ╞ P – assume / guarantee Assumption Environment E ╞ A – discharge the assumption how are assumptions obtained? Developer encodes them explicitly Abstractions of environment, if known

Approach Infer assumptions automatically Two novel solutions developed 1. Algorithmic generation of assumption; knowledge of environment is not required 2. Incremental assumption computation based on counterexamples, learning and knowledge of environment

Applications Verification produces more precise answers true – property satisfied in all environments false – property falsified in all environments assumption A – property true in environments where A is true Support for compositional verification Property decomposition Assumptions for assume-guarantee reasoning Runtime monitoring of environment assumption monitors actual environment during deployment may trigger recovery actions Component retrieval, sub-module construction, …

Solution 1 in collaboration with Prof. Howard Barringer, Univ. of Manchester, UK Giannakopoulou, D. , Păsăreanu, C. , and Barringer, H. , “Assumption Generation for Software Component Verification”, in Proc. of the 17 th IEEE International Conference on Automated Software Engineering (ASE 2002). Awards: Best paper, ACM Distinguished Paper Award

The Problem Given component C, property P, and the interface of C with its environment, generate the weakest environment assumption A such that: assuming A, C ╞ P Weakest means that for all environments E: (E || C ╞ P) IFF E╞ A

Implementation Labeled Transition Systems Analyzer (LTSA) Components modeled as labelled transition systems (LTSs) – communicate by rendezvous through shared actions – internal actions represented by action “ τ ” Compositional reachability analysis – hiding of internal actions – minimization w. r. t. observational equivalence Properties also expressed as LTSs Describe all legal behaviors – Deterministic – Completed for verification – bad behaviors lead to “error state” Composed with components – verification is postponed until the system is “closed” An LTS can be used as a property or an assumption

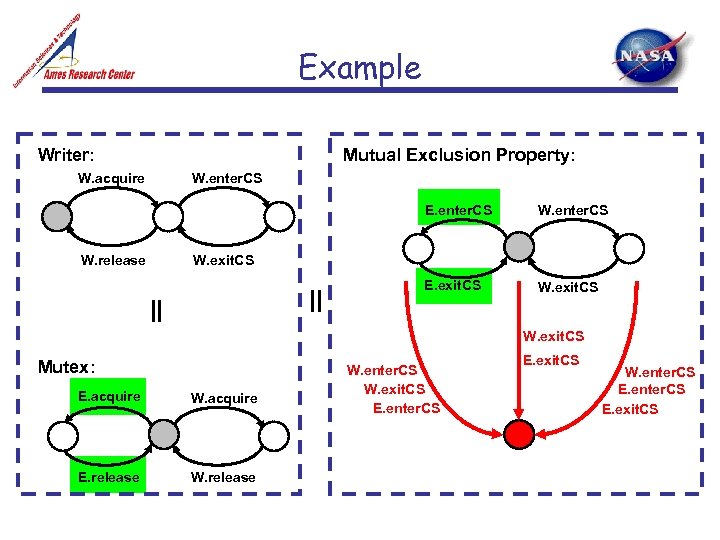Example Mutual Exclusion Property: Writer: W. acquire W. enter. CS E. enter. CS W. enter. CS E. exit. CS W. release || || W. exit. CS Mutex: E. acquire W. acquire E. release W. enter. CS W. exit. CS E. enter. CS E. exit. CS W. enter. CS E. exit. CS

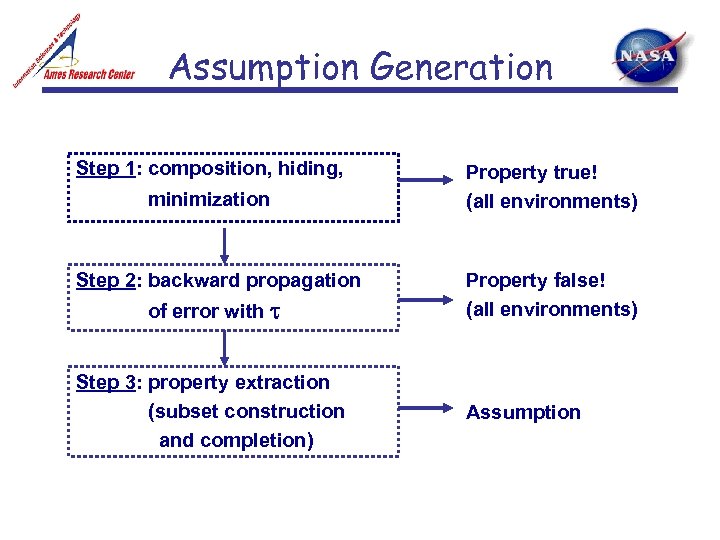Assumption Generation Step 1: composition, hiding, minimization Step 2: backward propagation of error with Step 3: property extraction (subset construction and completion) Property true! (all environments) Property false! (all environments) Assumption

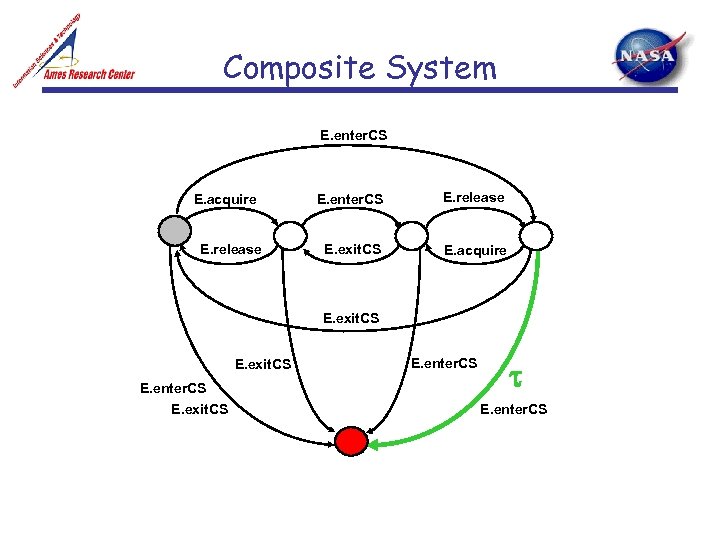Composite System E. enter. CS E. acquire E. release E. enter. CS E. release E. exit. CS E. acquire E. exit. CS E. enter. CS

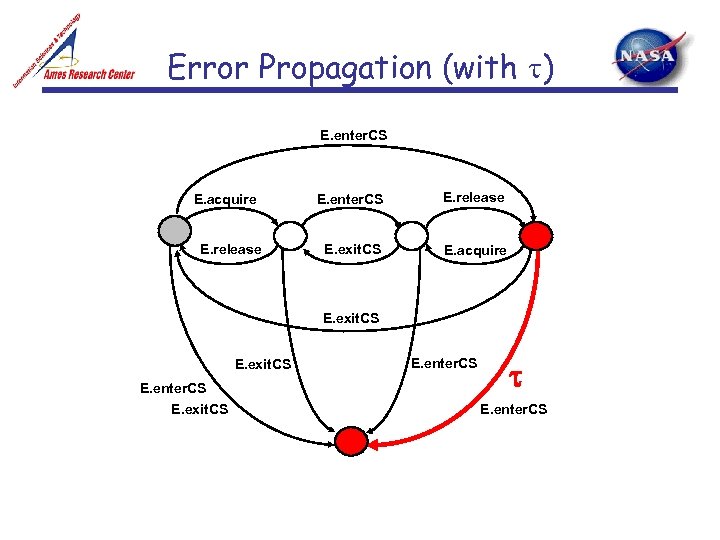Error Propagation (with t) E. enter. CS E. acquire E. release E. enter. CS E. release E. exit. CS E. acquire E. exit. CS E. enter. CS

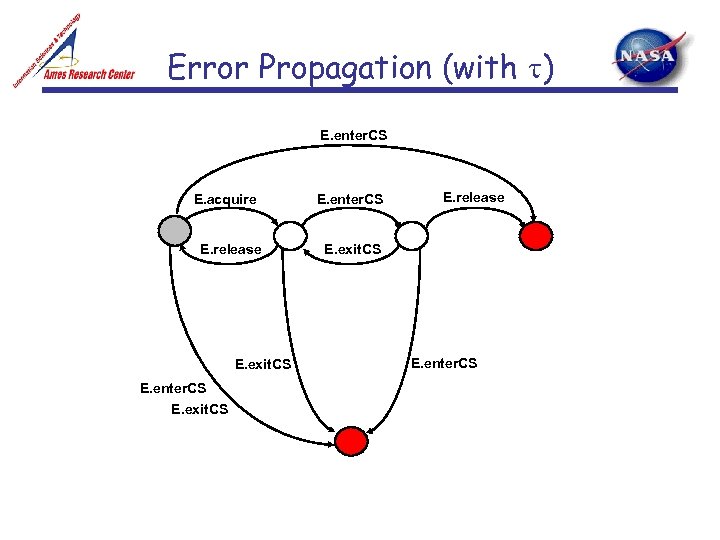Error Propagation (with t) E. enter. CS E. acquire E. release E. exit. CS E. enter. CS

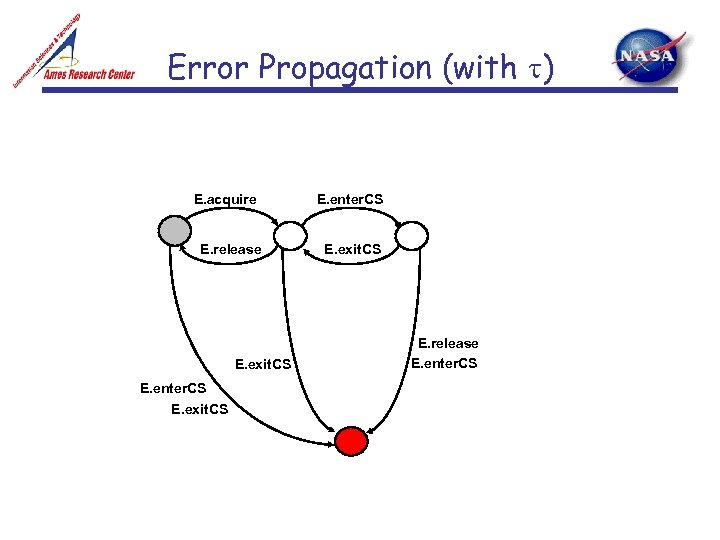Error Propagation (with t) E. acquire E. release E. exit. CS E. enter. CS E. exit. CS E. release E. enter. CS

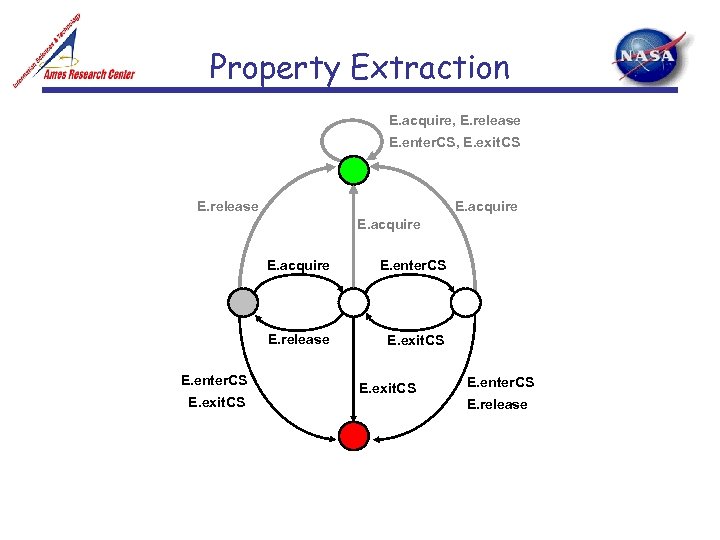Property Extraction E. acquire, E. release E. enter. CS, E. exit. CS E. release E. acquire E. release E. enter. CS E. exit. CS E. enter. CS E. release

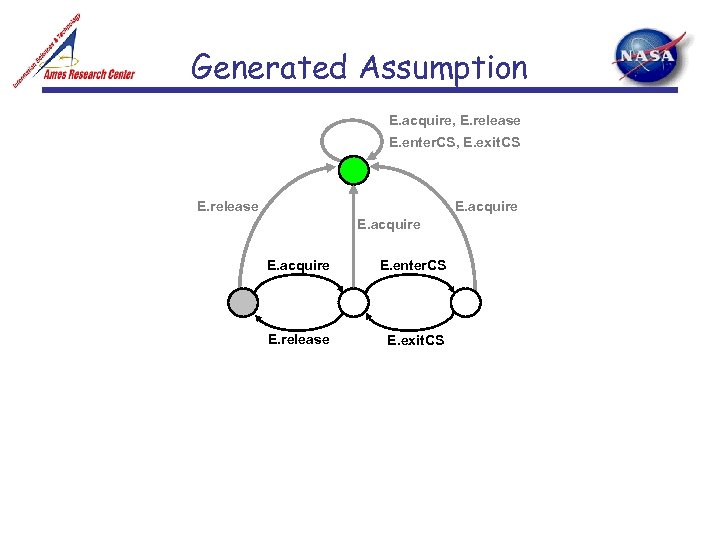Generated Assumption E. acquire, E. release E. enter. CS, E. exit. CS E. release E. acquire E. enter. CS E. release E. exit. CS

Ames Rover Executive Executes flexible plans for autonomy branching on state / temporal conditions Multi-threaded system communication through shared variables synchronization through mutexes and condition variables Systematic translation of design documents into input language of LTSA Several synchronization issues mutual exclusion data races properties specified by developer

Properties First property: mutual exclusion – 426 states {hiding + minimization} 18 states – assumption: 12 states Second property: If the Executive threads the value of variable saved. Wakeup. Struct, the Exec. Cond. Checker thread should not read this value unless the Executive clears it first. {hiding + minimization} – 544 states – assumption: 6 states 10 states

Resulting Assumption_Property 2 = Q 0, Q 0 = ( external. exec. lock -> Q 2), not displaying Q 2 = ( external. exec. unlock -> Q 0 sink state Q 1 | external. saved. Wakeup. Struct. read[1] -> Q 3 | external. saved. Wakeup. Struct. assign[0] -> Q 4 | external. saved. Wakeup. Struct. read[0] -> Q 5), Q 3 = ( external. saved. Wakeup. Struct. read[1] -> Q 3 | external. saved. Wakeup. Struct. assign[0] -> Q 4), Q 4 = ( external. exec. unlock -> Q 0 | external. saved. Wakeup. Struct. assign[0] -> Q 4 | external. saved. Wakeup. Struct. read[0] -> Q 5), Q 5 = ( external. saved. Wakeup. Struct. assign[0] -> Q 4 | external. saved. Wakeup. Struct. read[0] -> Q 5).

Solution 2 in collaboration with RIACS SSRP student Jamieson Cobleigh, Univ. of Massachusetts, Amherst Cobleigh, J. M. , Giannakopoulou, D. , and Pasareanu, C. S. “Learning Assumptions for Compositional Verification”, in Proc. of the 9 th International Conference on Tools and Algorithms for the Construction and Analysis of Systems (TACAS 2003). April 2003, Warsaw, Poland.

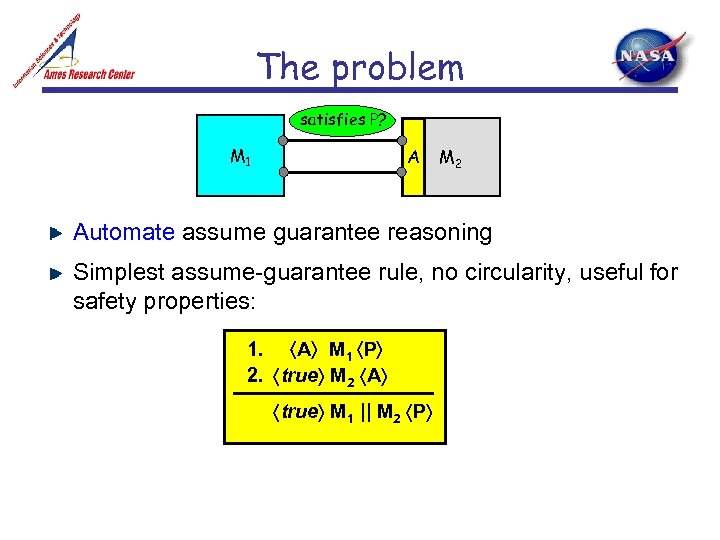The problem satisfies P? M 1 A M 2 Automate assume guarantee reasoning Simplest assume-guarantee rule, no circularity, useful for safety properties: 1. A M 1 P 2. true M 2 A 3. true M 1 || M 2 P

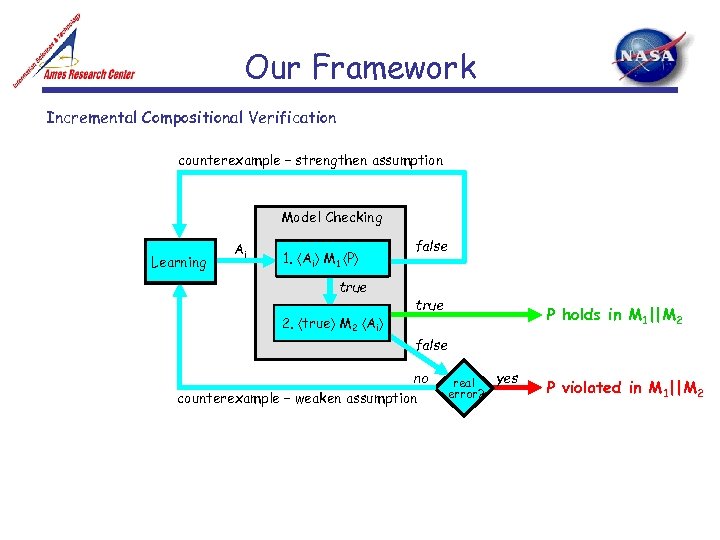Our Framework Incremental Compositional Verification counterexample – strengthen assumption Model Checking Learning Ai 1. Ai M 1 P true 2. true M 2 Ai false true P holds in M 1||M 2 false no counterexample – weaken assumption yes real error? P violated in M 1||M 2

Learning with L* L* – learning algorithm by Angluin, improved by Rivest & Schapire based on queries and counterexamples learns an unknown regular language (U over alphabet ) and produces a DFA C such that L (C) = U constructs a sequence of DFAs C 1, C 2, … converging to C needs a Teacher to answer two types of questions: membership queries: is string s in U ? conjectures: for a candidate DFA Ci, is L(Ci) = U ? – answers are (true) or (false + counterexample)

The L* Algorithm General method: maintains a table that records whether strings in belong to U makes membership queries to update it decides to make a conjecture – uses table to build a candidate Ci if Teacher replies true, done! if Teacher replies false, uses counterexample to update the table Characteristics: terminates with minimal automaton C for unknown language U each candidate Ci is smallest any DFA consistent with table has at least as many states as Ci |C 1| < | C 2| < … < |C| produces at most n candidates, where n = |C|

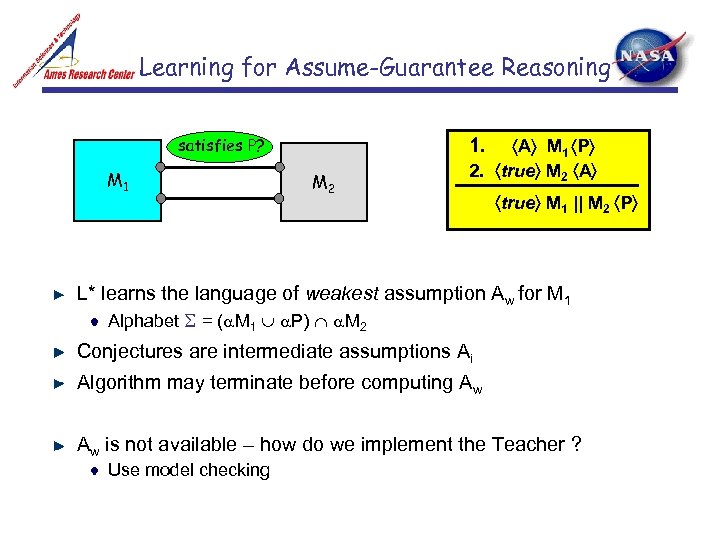Learning for Assume-Guarantee Reasoning satisfies P? M 1 1. M 2 A M 1 P 2. true M 2 A 3. true M 1 || M 2 P L* learns the language of weakest assumption Aw for M 1 Alphabet = ( M 1 P) M 2 Conjectures are intermediate assumptions Ai Algorithm may terminate before computing Aw Aw is not available – how do we implement the Teacher ? Use model checking

The Teacher Membership query: trace s Simulate s on M 1 || Perr – If it leads to error state, reply false ( s L(Aw) ) – Otherwise, reply true ( s L(Aw) ) Conjecture: Ai Oracle 1: performs (Step 1) Ai M 1 P – If false (with counterexample c): provide c to L* (assumption is too weak) – If true: forward Ai to Oracle 2: performs (Step 2) true M 2 Ai – If true: done! (P holds on M 1 || M 2) – If false (with counterexample c): forward c to analysis Counterexample analysis Simulate c on M 1 || Perr – If it leads to the error state: done! (P does not hold on M 1 || M 2) – Otherwise, provide c to L* (assumption is too strong)

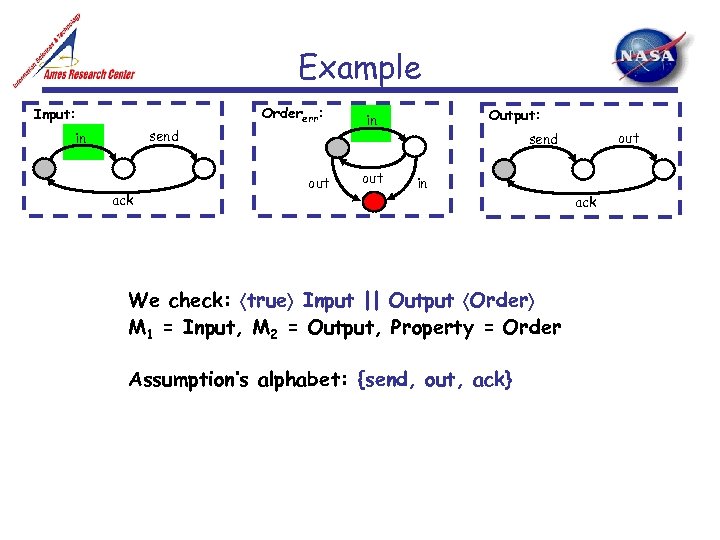Example Ordererr: Input: send in ack out Output: in out send in We check: true Input || Output Order M 1 = Input, M 2 = Output, Property = Order Assumption’s alphabet: {send, out, ack} ack

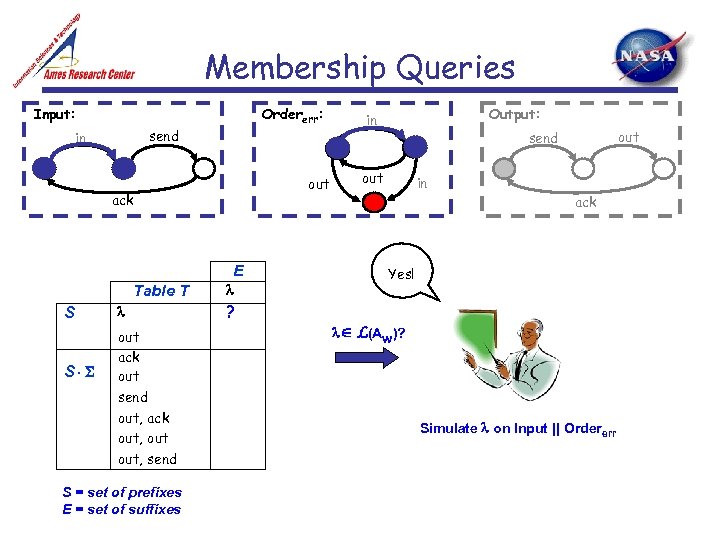Membership Queries Input: Ordererr: send in out ack E Table T S S out ack out send out, ack out, send S = set of prefixes E = set of suffixes ? Output: in out send out in ack Yes! L(Aw)? Simulate on Input || Ordererr

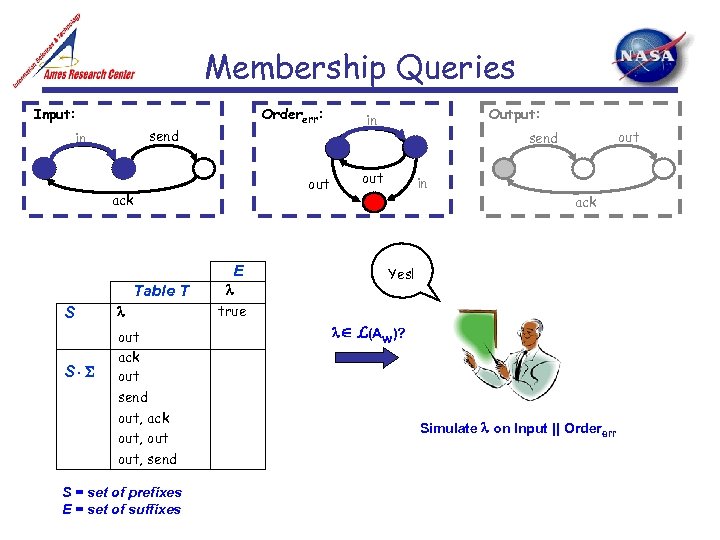Membership Queries Input: Ordererr: send in out ack E Table T S S out ack out send out, ack out, send S = set of prefixes E = set of suffixes true Output: in out send out in ack Yes! L(Aw)? Simulate on Input || Ordererr

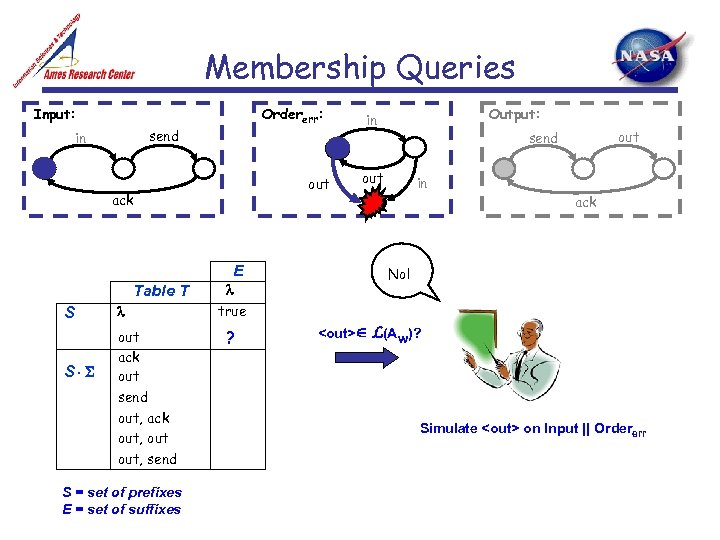Membership Queries Input: Ordererr: send in out ack E Table T S S out ack out send out, ack out, send S = set of prefixes E = set of suffixes true ? Output: in out send out in ack No! L(Aw)? Simulate on Input || Ordererr

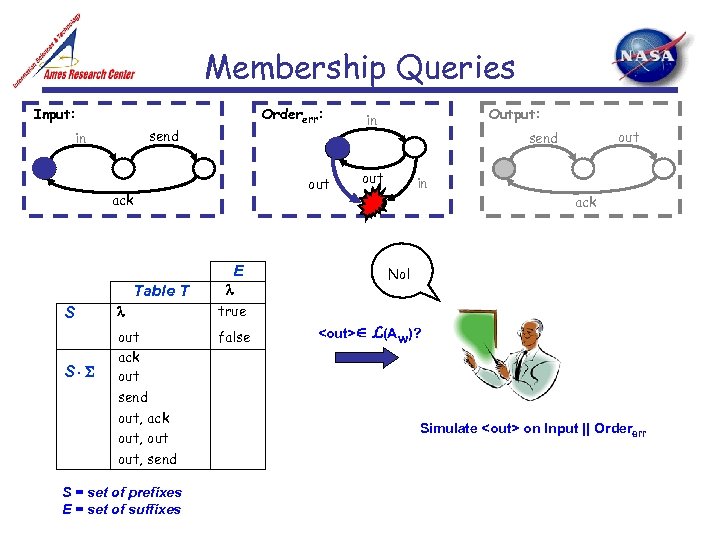Membership Queries Input: Ordererr: send in out ack E Table T S S true out ack out send out, ack out, send false S = set of prefixes E = set of suffixes Output: in out send out in ack No! L(Aw)? Simulate on Input || Ordererr

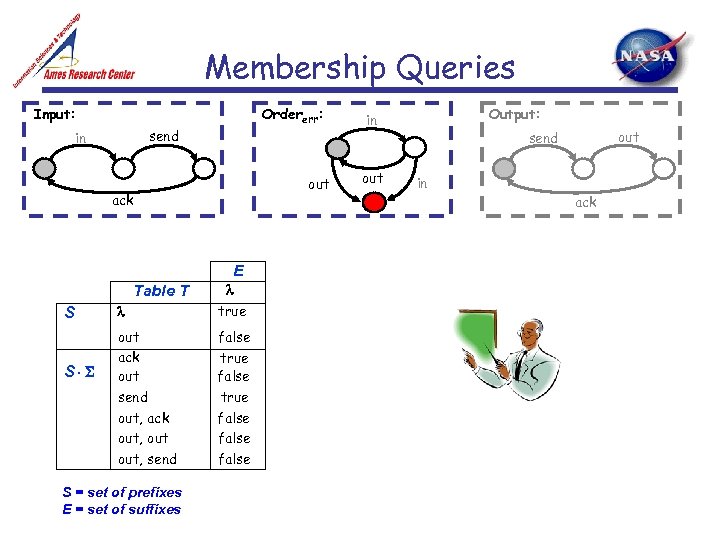Membership Queries Input: Ordererr: send in out ack E Table T S S true out ack out send out, ack out, send false S = set of prefixes E = set of suffixes true false Output: in out send in ack

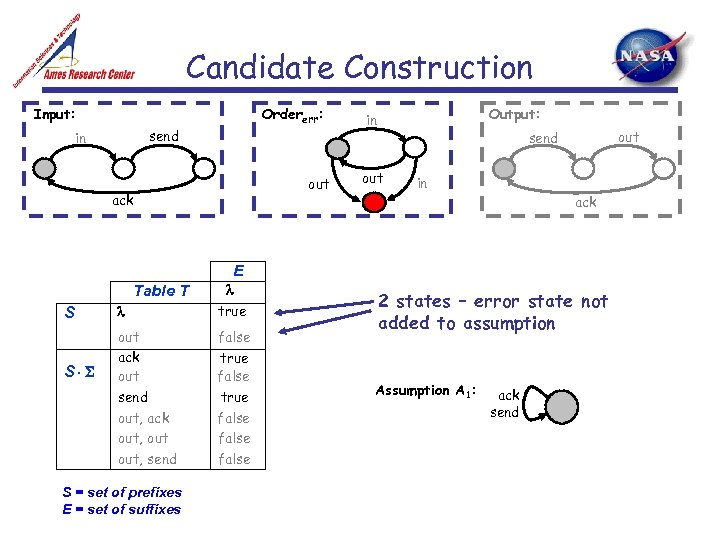Candidate Construction Input: Ordererr: send in out ack Output: in out send in ack E Table T S S true out ack out send out, ack out, send false S = set of prefixes E = set of suffixes true false 2 states – error state not added to assumption A 1: ack send

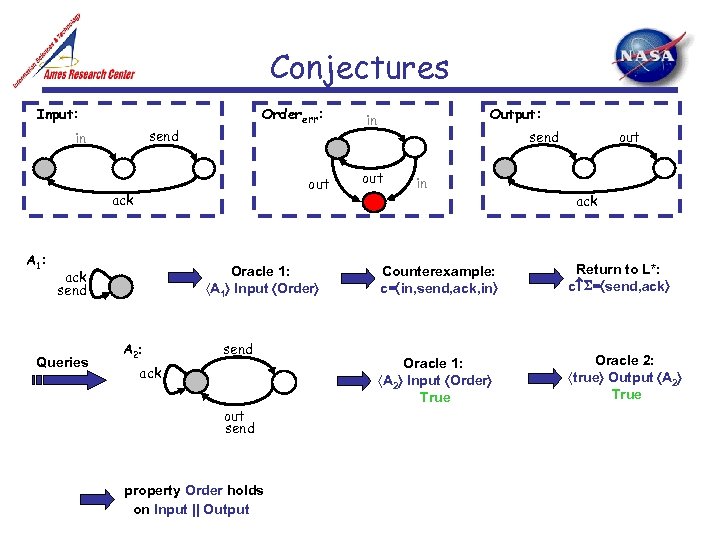Conjectures Input: Ordererr: send in out ack A 1: Oracle 1: A 1 Input Order ack send Queries A 2: send ack out send property Order holds on Input || Output: in out send out in ack Counterexample: c= in, send, ack, in Return to L*: c = send, ack Oracle 1: A 2 Input Order True Oracle 2: true Output A 2 True

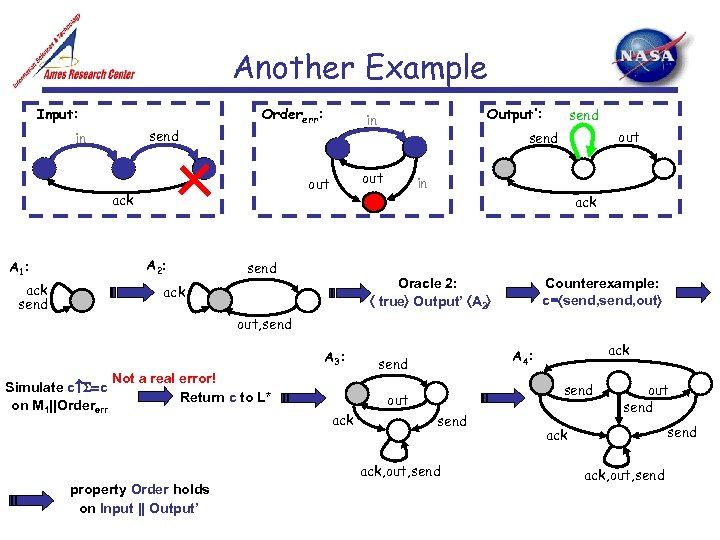Another Example Input: Ordererr: send in A 1: ack send A 2: send out in ack Oracle 2: true Output’ A 2 ack send out ack Output’: in Counterexample: c= send, out, send A 3: Not a real error! Simulate c =c Return c to L* on M 1||Ordererr ack send out send ack, out, send property Order holds on Input || Output’ ack A 4: out send ack, out, send

Case Study: K 9 Rover again iteration |Ai| (#states, #trans) result 1 – Oracle 1 1 (5, 24) too weak 2 – Oracle 1 2 (268, 1408) too weak 3 – Oracle 1 3 (235, 1209) too weak 4 – Oracle 1 5 (464, 2500) not too weak (32, 197) false Oracle 2

Comparisons Pentium III, 500 MHz, 1 Gb of memory check P on M 1 || M 2 » (3630 sts, 34653 trans), 0. 535 secs. using weakest assumption 6 states generation: (544 sts, 6314 trans), 24. 623 secs discharging assumption: (32 sts, 197 trans), 0. 504 secs using incremental assume-guarantee reasoning 5 states (max: 464 sts, 2500 trans), 8. 639 secs

Related Work Interface automata (de Alfaro, Henzinger) component compatibility Assume-guarantee frameworks MOCHA, Calvin (extended static checking of Java), … Interfaces for Compositional Reachability Analysis Graf-Steffen-Lüttgen, Cheung-Kramer, Krimm-Mounier Controller synthesis Interface equation / sub-module construction Merlin-Bochmann, Shields, Parrow, Larsen-Xinxin Synthesis of deadlock-free connectors Inverardi-Scriboni-Wolf-Yankelevich

Conclusions & Extensions Model checking components as open systems Assumptions can be further analyzed do components that implement them, or the resulting system, have any useful behavior? Incremental framework is general relies on standard features of model checkers experimenting with JPF More case studies Learning box – improve / change algorithm? Extended properties (deadlock, liveness, fairness) Timed systems

Contact {dimitra, pcorina} @ email. arc. nasa. gov http: //ase. arc. nasa. gov/

DEMO

Contact {dimitra, pcorina} @ email. arc. nasa. gov http: //ase. arc. nasa. gov/